基于UKF的航天器双行根数转换方法
2021-04-27龚秋武毛永军杨舒农陈鼎白云
龚秋武 毛永军 杨舒农 陈鼎 白云
(1 中国酒泉卫星发射中心, 甘肃酒泉 732750)(2 中国人民解放军95983部队, 甘肃酒泉 732750)
据统计,截止2019年10月4日,太空中约有19 779个直径超过10 cm的空间物体,其中包括5181个航天器和14 598个空间碎片[1],这些都对正常运行的航天器的安全构成了极大的威胁。因此,规避空间碎片已成为一项非常重要的应急航天任务。而该任务的前提是确定航天器的轨道根数,并预测其轨道,以确定它是否会与轨道附近的空间碎片相撞。此外,当某些自然灾害发生时,例如火山爆发、地震和森林火灾等,无法在地面上观察到灾害现场。但是,侦察卫星和遥感卫星等航天器却可用于这种应急空间侦察任务,但前提也是要先确定其轨道根数,以便计算它们何时飞行到灾害发生地的上空,从而开展空间侦察和探测。
对于航天器的轨道根数确定,美国空军太空司令部(Air Force Space Command,AFSPC)发布的双行根数(Two Line Elements,TLEs)可能是最准确的描述[2-3]。TLEs不是瞬时轨道根数,而是通过特殊方式消除周期性变化得到的“平均轨道根数”;TLEs具有标准化的格式,并且只能与SGP轨道模型配套使用。此外,应急航天任务还强调实时与自主性,以满足时效性的要求。传统的轨道确定方法将星上导航数据传输到地面站进行计算,然后再将结果传输到航天器。尽管其结果具有较高的精确度,但占用大量计算资源,且消耗大量时间进行数据传输。因此,当考虑到实时性和星载计算能力时,传统的轨道确定方法对于应急航天任务是不可接受的[4-5]。
实际上,绝大多数轨道模型,例如二体模型、J2扰动和高精度轨道预测(High Precision Orbit Prediction,HPOP)模型等,都使用瞬时轨道根数进行轨道预报[6]。但是,TLEs是“平均”轨道根数,与瞬时轨道根数不同,尽管这两种轨道根数非常相似,但是如果将TLEs替换为瞬时轨道根数代入SGP模型进行轨道预报,将会造成较大的预报误差。因此,将瞬时轨道根数转换为TLEs是非常必要的。但是,AFSPC并没有公布这两种轨道根数相互转换的算法。为了解决这个问题,必须建立对应的算法将瞬时轨道根数转换为可以用于SGP的双行根数[7]。
文献[8]建立了SGP4模型,并用于近地卫星轨道预报,将文献[9]的解析理论进行简化,将重力模型和空气动力学模型作为Brouwer和功率密度函数的解,便可以得到SGP4模型。该模型考虑了几个长期和长周期扰动项,例如,J2,J3和J4项和空气阻力等,以确保轨道预报的精度。但是由于未考虑短周期扰动项,SGP4模型的位置预报精度只能达到2 km[10]。文献[11]根据TLEs和SGP4模型开发了一个轨道预报软件包。文献[12-13]提出了瞬时轨道根数和平均轨道根数之间的一种转换方法。为了提高太空飞行的安全性,文献[14-15]建立了基于SGP4和TLEs的空间碎片轨道预测方法。文献[16]提出了两种方法来修改TLEs的阻力系数,并将SGP4的预测精度提高了20%以上。文献[17]对LEO碎片的阻力系数进行研究,并估计了2000多个空间碎片的阻力系数来检验TLEs的精度。文献[18]运用批量最小二乘技术和测距率来校正历元时刻的TLEs角度误差,提高了圆形轨道确定的准确性。由于上述研究仅研究了TLEs部分元素的解算和转换方法,因此需要对其他元素的解算和转换开展更多研究。
本文即以航天器双行根数为状态变量,以飞行位置和速度为测量变量,提出基于无迹卡尔曼滤波的航天器双行根数转换方法,有效转换得到TLEs的基本元素[19],且达到TLEs格式的精度要求。
1 建模与坐标转换

(1)
式中:s(t)、r(t)和v(t)都是矢量,用列向量表示;S(·)代表SGP4模型;α0代表TLEs的元素;t代表从历元时刻t0开始的时间间隔。
(2)
已知SGP4模型和TLEs的参考坐标系为真春分点和平二分点(TEMED)参考系统。但是,导航数据的参考坐标系是世界大地测量系统(World Geodetic System 1984,WGS84)。因此,需要将导航数据经过两次坐标转换,从WGS84转换为J2000.0,再从J2000.0转换为TEMED。第一次转换可参考文献[20],第二次转换可参考文献[12]和[21]。
2 瞬时轨道根数与双行根数转换方法
文献[12]和[13]中,均提出了瞬时轨道根数转换为双行根数的迭代算法,算法根据航天器任意时刻的飞行状态矢量来实现瞬根与双行根数的转换。但是,迭代算法不能充分利用航天器的全部飞行状态数据;其次,由于在整个迭代过程中未更新用来对比的标准飞行状态矢量,因此无法消除测量噪声的影响;另外,迭代算法不能解算出TLEs中的大气阻力系数。
为了弥补上述算法的不足,充分利用航天器飞行状态数据并消除测量噪声的影响,本节建立卡尔曼滤波算法将瞬根转换为双行根数。卡尔曼滤波是基于状态估计理论而建立的,最常用的是在此卡尔曼滤波理论上发展而来的扩展卡尔曼滤波(Extended Kalman Filter,EKF)和无迹卡尔曼滤波(Unscented Kalman Filter,UKF)等。
本文基于UKF建立航天器双行根数转换方法,其中航天器双行根数是状态变量,而飞行状态是测量变量。UKF最特殊优势的是利用无迹变换(Unscented Transform,UT)而不是线性化来处理均值和协方差的传递[22]。对于UT,为了获取原始状态矢量的均值和协方差,选择了一组选定的sigma点。然后,通过非线性模型进行映射。接着,计算sigma点的均值和协方差。这样,对于任意的非线性函数[23-26],均值和协方差可以达到二阶精度。
未选择扩展卡尔曼滤波主要是考虑到EKF需要对非线性测量方程进行线性化,会产生线性化误差,严重时使得滤波发散,其次由于SGP4模型的复杂性与非线性,无法使用偏微分计算测量矩阵,而是用数值差商则会大量增加计算量。
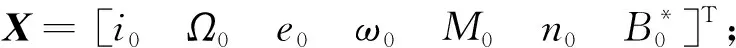
X(t)=I7X0
(3)
式中:X(t)表示t历元时刻双行根数;I7表示7维单位阵;X0表示初始历元时刻双行根数。
测量方程类似于式(1)
Z(t)=S(X0,t)+V
(4)

由于测量数据是离散的,因此可以将式(4)改为
Z(k)=rk=S(X0,k)r+V(k),(k=1,2,3…)
(5)
式中:S(X0,k)r表示离散状态的预测位置矢量,V(k)表示离散状态的测量噪声矢量。
sigma点及其权重通过式(6)和(7)计算
(6)
(7)

详细的过程可参考文献[26]。显然,UKF没有线性化。它实现了UT以使sigma点的均值和协方差与原始特征相匹配,然后将应用sigma点的非线性映射得到状态量的概率密度函数。
3 数值仿真
前两节中,建立了算法和模型,下面将通过数值仿真来验证有效性和准确性。航天器的参数是从STK软件的TLEs数据库中选择的,而测量数据是由STK仿真模拟得到的。选择tle-00005航天器来实施仿真(tle-00005航天器是STK软件包的TLEs数据库中的一个航天器,其名称为Vanguard1是美国海军在1958年3月17日发射的,周期约为133 min),由SGP4模型的特点可知,当轨道周期小于255 min时,SGP4的预报性能更好[2]。根据UKF算法仿真需要,挑选该航天器TLEs中的部分参数,如表1所示。
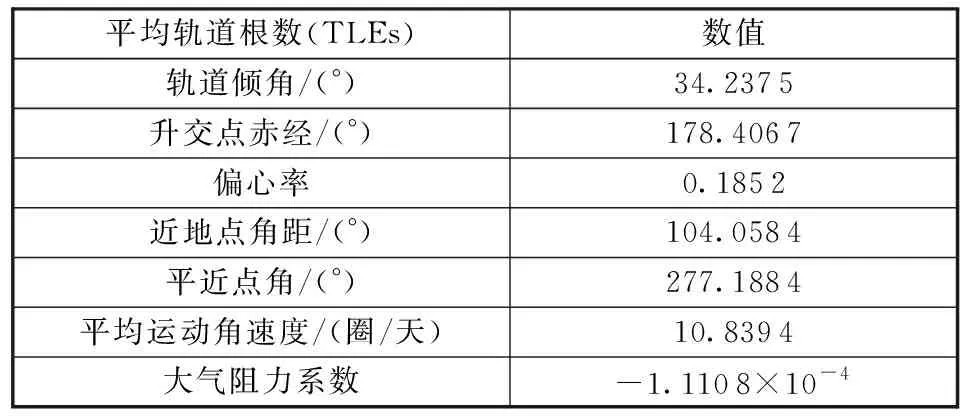
表1 tle-00005航天器双行根数Table 1 TLEs of tle-00005 spacecraft
滤波参数的设置决定了滤波器的性能,UKF的参数设置为

(8)
测量数据由STK仿真得到,且测量时间间隔设置为1 min。根据GPS和北斗等导航设备的定位精度可知,目前民用的定位精度约为10 m(σ)量级[27],因而测量噪声参数设置为
R=diag(10,10,10)
(9)
式中:diag(·)表示对角矩阵。
以一天为预报时长,分别利用STK软件和本文的程序进行轨道预报,将STK预报值作为标准值,通过叠加小量到TLEs上,使本文的程序预报值与标准值之间的位置误差约为1 m(σ/10),基于此,可以估计过程噪声矩阵。初始状态协方差的设置要避免滤波器发散,通过参考过程噪声来设置它。进而,给出过程噪声和初始状态协方差矩阵的值如下:
Q=diag(10-7,10-7,10-7,10-7,10-7,10-10,10-7)
(10)
P0=diag(10-7,10-7,10-7,10-7,10-7,10-7,10-7)
(11)
利用STK仿真,得到航天器在WGS84系中的飞行状态。任意选择一组状态量,本文中选取2007年5月18日05:02:19.609时刻(历元初始时刻)的位置和速度矢量,如表2所示(这些数据均不含测量噪声)。
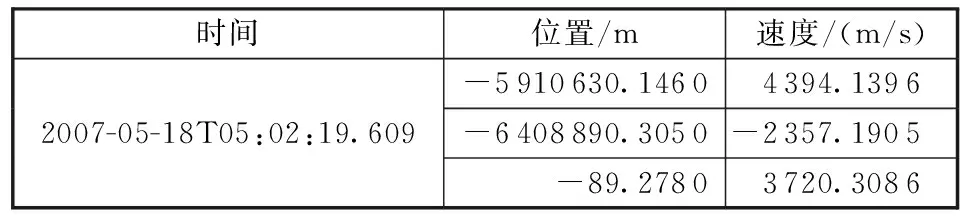
表2 tle-00005航天器的飞行状态参数 Table 2 Flight state of tle-00005 spacecraft
根据二体运动方程的轨道积分、活力积分等公式,可推导得到轨道根数与位置/速度的关系[28],利用无测量噪声的位置和速度数据,即可计算得到滤波状态初值的前6个参数,但第7个参数大气阻力系数无法通过该方法计算,因此该参数文中采用经验值,取为-1.000 0×10-4,则航天器双行根数的初始状态值为
(12)
然后代入UKF算法进行计算,并将得到的双行根数与表1的参考值进行比较,结果见表3和图1。其中图1横坐标的数字1~7分别代表轨道倾角、升交点赤经、偏心率、近地点角距、平近点角、平均运动角速度和大气阻力系数等7个TLEs参数(均转换为误差大小,不含符号)。选择偏心率和平均运动角速度的绝对误差曲线来展示UKF滤波过程,如图2所示。

表3 UKF算法结果Table 3 Results of UKF

图1 UKF精度(误差大小,不含符号)Fig.1 Accuracy of UKF results (without sign)
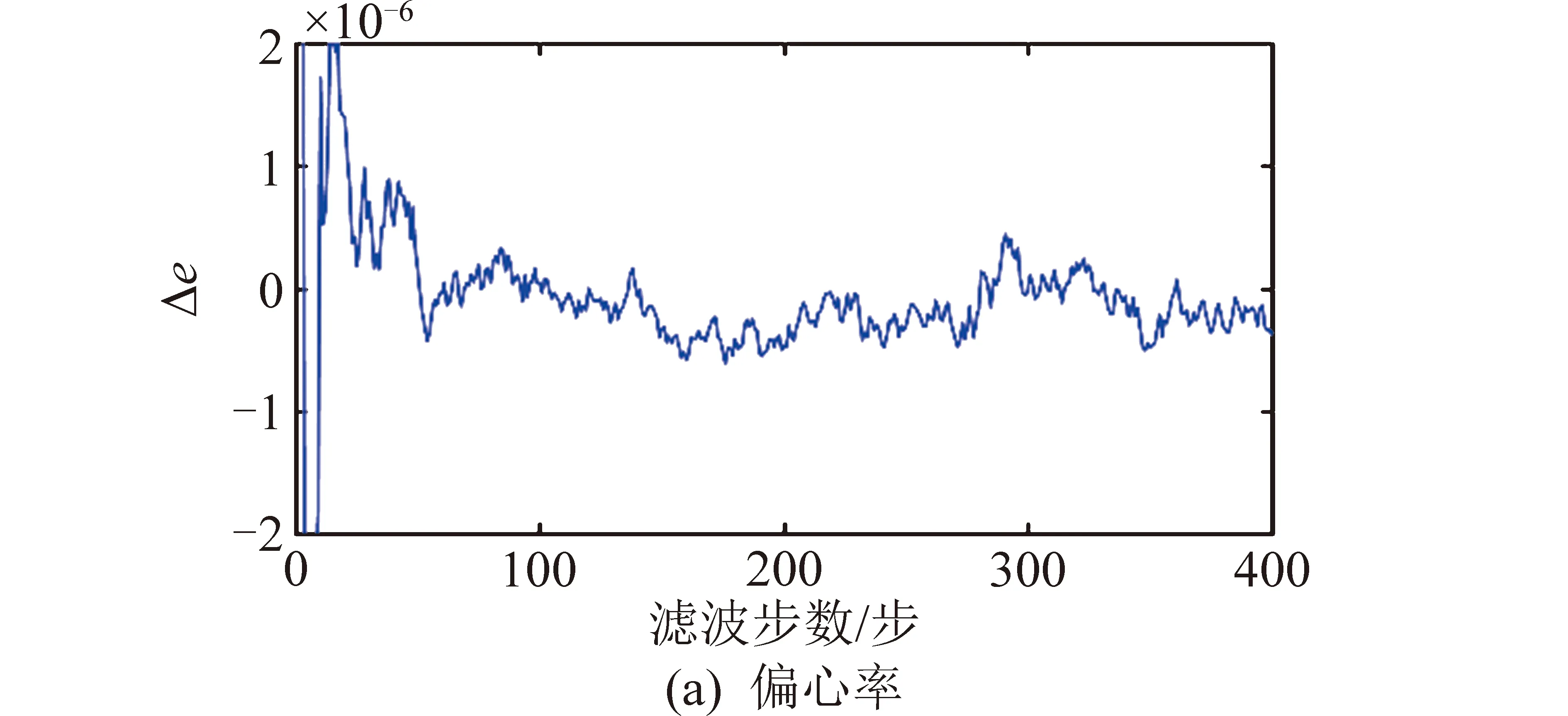

图2 UKF的滤波过程Fig.2 Procedure of UKF
从表3和图2可知,UKF能有效将瞬根转换为双行根数。当测量噪声位置误差为10 m时,4个角度的精度至少为10-5(°),偏心率精度为10-7,平均运动角速度精度为10-9圈/天,大气阻力系数精度为10-6。
此外,使用滤波算法的结果进行轨道预报并与STK值进行比较,结果如图3所示,位置误差在10 m以内,速度误差在0.008 m/s以内。可以推断,当测量噪声较小时,UKF精度很高。
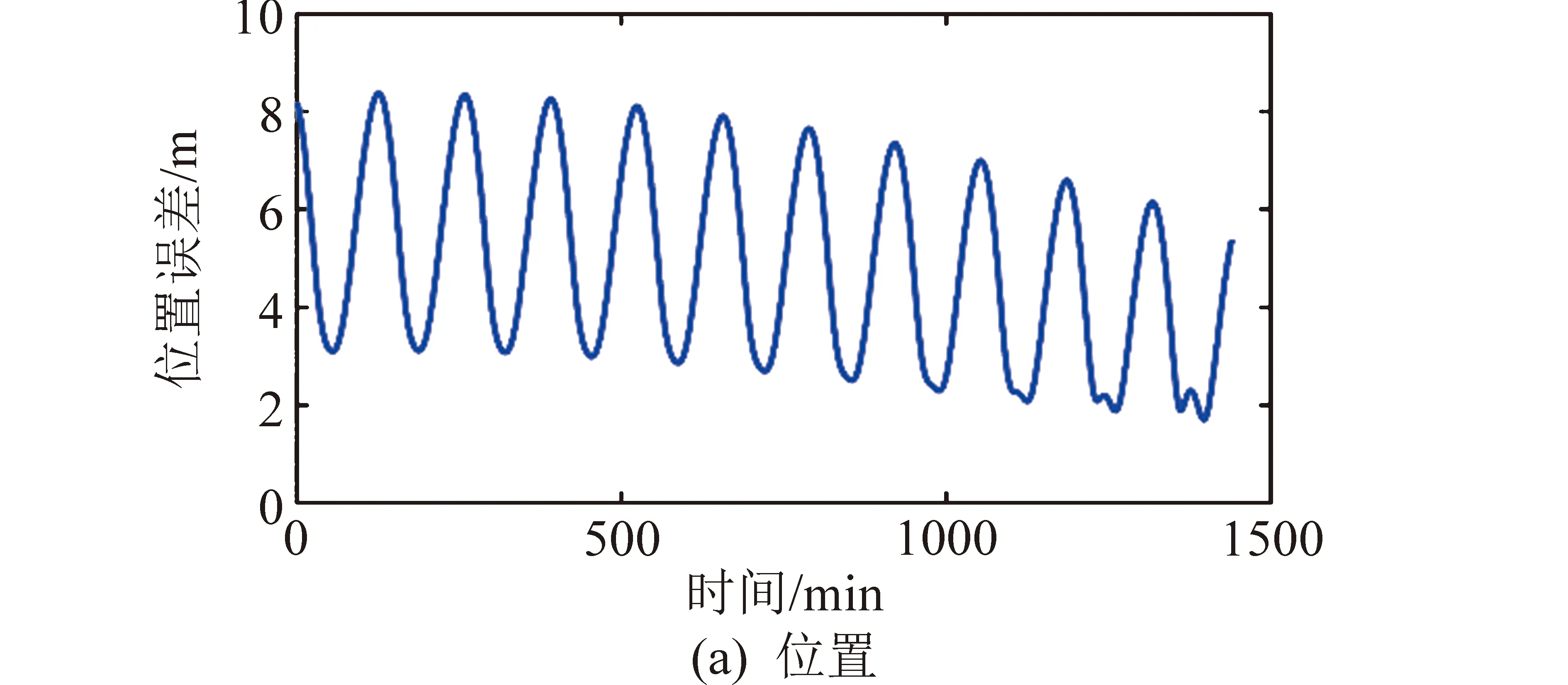
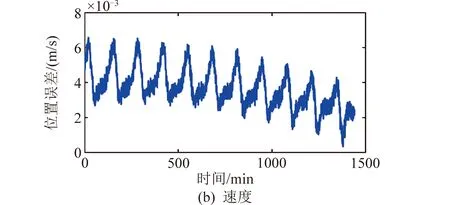
图3 利用UKF结果进行轨道预报的位置和速度误差Fig.3 Position and velocity propagation deviations of UKF results
为了说明大噪声对滤波算法的影响,下面叠加噪声到导航数据中然后再进行仿真。类似地,噪声的均值设置为零,而方差分别设置为3σ和10σ,其中σ=10。结果的绝对误差如图4所示,其中横坐标的数字1~7所表示的参数与图1相同。将结果代入SGP4模型进行轨道预报并与STK值相比较,得到的位置和速度预报误差如图5所示。


图4 测量噪声对滤波算法的影响(误差大小,不含符号)Fig.4 Influence of measurement noise to filter algorithm (without sign)




图5 利用UKF在大噪声条件下的结果进行轨道预报的位置和速度误差Fig.5 Position and velocity propagation deviations of UKF results under big noise condition
从图4、5可知,TLEs的绝对误差以及位置和速度预报误差均随着噪声方差的增大而增大。但是在两个仿真算例中,位置预报误差均小于测量噪声的方差。
对于其他特殊情况,如较大的初始误差,同样进行了数值仿真。通过之前仿真,可以知道初始状态值是由二体模型在导航数据不包含测量噪声条件下计算得到的。在此,对用来计算初始状态的导航数据叠加噪声,然后再利用二体模型计算初始状态,从而进行较大初始误差情况的数值仿真。
测量噪声的均值设置为零,方差分别设置为10σ和100σ,其中σ=10[28],其他参数设置与正常情况一致,仿真结果如表4所示。

表4 大初始误差条件下的结果Table 4 Results under large initial error condition
从表4中可以看出,在较大初始误差条件下,UKF算法仍可以得到满足TLEs格式精度的航天器双行根数。
4 结束语
本文研究了基于无迹卡尔曼滤波的航天器双行轨道根数转换方法。在较小测量噪声条件下,UKF性能很高。当测量噪声位置误差为10 m时,UKF的结果,4个角度的精度为10-5(°),偏心度精度为10-7,平均运动角速度精度为10-9圈/天,大气阻力系数精度为10-6,均达到了TLEs标准格式的精度要求。利用转换得到的TLEs进行轨道预报,在一天时间内,位置预报误差在10 m以内,速度预报误差均在0.008 m/s以内。在某些特殊情况下,如较大初始误差和较大测量噪声,UKF仍能有效转换得到满足精度要求的航天器双行根数。
