A New Efficient Numerical Method for Pricing American Options on Zero-coupon Bonds
2021-04-26GANXiaotingYIHua
GAN Xiaoting, YI Hua
(1. School of Mathematics and Computer Science,Chuxiong Normal University, Chuxiong, Yunnan 675000;2. Department of Mathematics, Jinggangshan University, Ji’an, Jiangxi 343009)
Abstract: Unlike the European options pricing, the closed-form solution generally does not exist due to the early exercise feature of American options. Hence, numerical approximation methods are normally employed to solve them. Presented in this paper is a new numerical method to price American bond options. To numerically solve the resulting partial differential complementarity problem (PDCP), we develop a class of finite volume method for the spatial discretization, coupled with the stable fully implicit time stepping scheme of the partial differential equation(PDE).Then,the resulting linear complementarity problems (LCPs) are solved by using an effi-cient iterative method,the modulus-based matrix splitting iteration method,where the H+-matrix property of the system matrix guarantees its convergence. Numerical experiments are implemented to verify the accuracy, efficiency and robustness of the new method.
Keywords: American bond option; finite volume method; linear complementarity problems;modulus-based matrix splitting iteration method
0 Introduction
Pricing and hedging of interest rate derivatives, such as bond options, have been increasingly attracting much attention during the last two decades. Unlike a stock derivative, a bond option has a bond as its underlying asset whose price depends on both interest rates and time, hence the valuation of bond options is a very challenging task. For European bond options,it is possible to derive the analytical formulas for their prices directly[?]. While for the American bond options pricing,a so-called early exercise constraint is posed, which makes the pricing problem has no analytical solutions[?].Consequently, the American bond options pricing problems can be formulated as free boundary problems or variational inequality problems, then the efficient and robust numerical methods are usually required[?].
In general,numerical methods for pricing American options consist two tasks which are the discretization of the underlying PDE and the solutions of the resulted large sparse LCP.In the last twenty years,numerical solutions of the American bond options have been studied by various approximation techniques,for instance,lattice method[?],full-implicit and implicit-explicit finite difference methods[?], a direct discrete-time approach[?],explicit finite difference method[?],finite volume method combined with the Brennan-Schwartz algorithm and the penalty method[8–9], finite element method[10–11],two-GJ approach[?], spectral method[?], fitted finite volume method[?,?,?,?], etc. Compared with other aforementioned methods,the finite volume method usually possesses a special feature of local conservation of the numerical fluxes, and has been gaining popularity. In this work, we adopt the accurate and stable finite volume scheme. On the other hand,much attention has been paid on the numerical solutions of the large sparse LCP, for instance, multisplitting iteration methods[?], projected relaxation methods[?],penalty methods[?,?]. Recently, the modulus-based matrix splitting iteration methods for solving LCP studied by Bai have attracted a great deal of attention for the good performance in actual computation[?]. By transforming the original idea in [?] as an implicit fixed-point equation based on a splitting of the system matrixA,these methods not only provide a general framework for the modified method[?]and nonstationary extrapolated modulus algorithms[?], but also yields a series of modulus-based relaxation methods. For more recent survey on modulus-based matrix splitting iteration methods,we refer the reader to [?,?,?,?,?] and the references therein.
Motivated by the modulus-based matrix splitting iteration methods for LCP, the modulus-based successive overrelaxation (MSOR) method combined with the finite difference method and finite volume method has been extended for pricing Black-Scholes American options[?]and American jump-diffusion options[?], respectively. Based on these results, we derive a class of finite volume scheme combined with the modulusbased matrix splitting iteration method to price American options on a zero-coupon bond in this paper. We apply a finite volume scheme in space, along with the fully implicit scheme in time. And then,the modulus-based matrix splitting iteration method is used to solve the resulting large sparse LCP. We will also show that theH+-matrix property of the system matrix guarantees its convergence. Numerical experiments verify that the proposed methods are efficient and robust.
The rest of this paper is organized as follows. In section 1, American option on a zero-coupon bond model is briefly reviewed. Then, the finite volume discretization and some theoretical analyses are presented in section 2. In section 3, we introduce the modulus-based matrix splitting iteration method and investigate its convergence for the LCP. Numerical experiments are reported in section 4, and section 5 provides a brief conclusion.
1 Mathematical model for American bond option
In this section,we briefly describe the mathematical model for pricing American put option on a zero-coupon bond. We assume that the short term interest rate (denoted by ‘r’) structure is governed by the Cox-Ingrosll-Ross (CIR) model, i.e.,ris governed by the following mean-reverting version of the square-root process
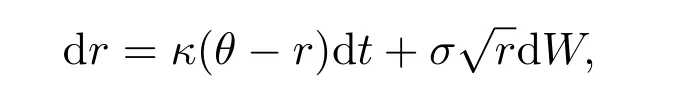
where dWis the increment of a Wiener process,θis the long term level of the short rate,κ >0 stands for the reversion speed,σ2ris the variance withσ >0. In [?], it has been shown that the priceP(r,t,s) of a pure discount bond with face value $1 at its maturity datesis given as follows

andζis the market risk premium. At the maturity dates, the price of a pure discount bond equals to its face value, i.e.,
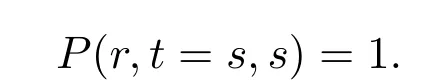
LetV(r,t) be the value of an European put bond option with striking priceK,where the holder can receive a given payoffΛ(r,t) at the expiry dateT. Introducing a time-reverse transformationτ=T-t, then the valueV(r,τ) can be governed by the following PDE
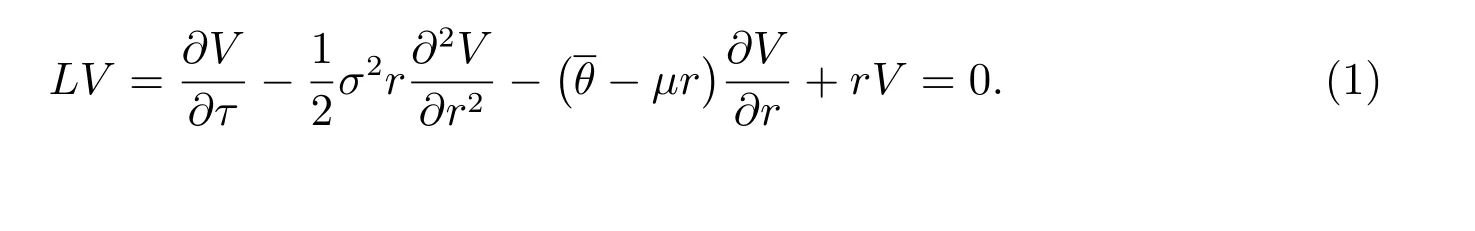

2 The finite volume method


2.1 Semi-discrete finite volume scheme
The semi-discrete finite volume scheme for problem (??) is: findVh=Vh(·,τ)∈Sh(0≤τ ≤T) such that
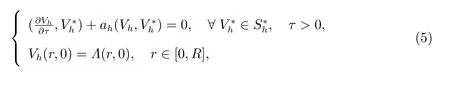



Summarizing (??)~(??), we conclude that S has non-positive off-diagonal and positive diagonal entries, and is strictly diagonally dominant. Hence, the semi-discrete matrix S is anH+-matrix.
2.2 Full discretization finite volume scheme
Now,we consider the time discretization of (??). Letτn=nΔτforn=0,1,··· ,N,whereNis a positive integer and Δτ=T/N. For simplicity,we apply the fully implicit scheme to (??), yields
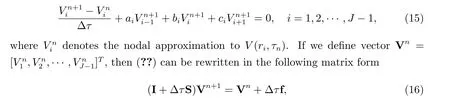
where I represents an (J-1)×(J-1) unit matrix.
We comment that in (??), the Dirichlet boundary conditions (??) atr= 0 andr=Rhave been incorporated. Also, the initial condition is incorporated as the payofffunction, i.e., V0=Λ. The vectorΛcontains the values of the payofffunctionΛ(r,0)at the grid points.
For the fully implicit scheme (??), the stability result is given as follows.
Theorem 2 The fully implicit finite volume scheme (??) is stable, i.e.
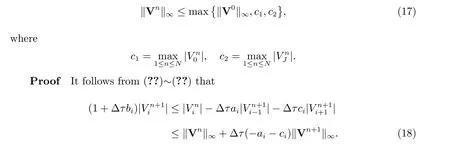
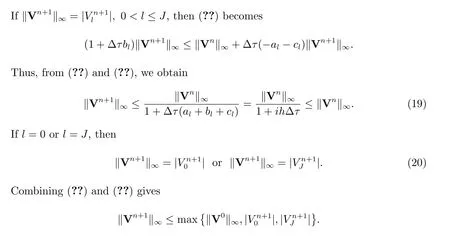
which then results in(??). Hence the fully implicit finite volume scheme(??)is stable.
The following corollary can be obtained from Theorem 1 directly.
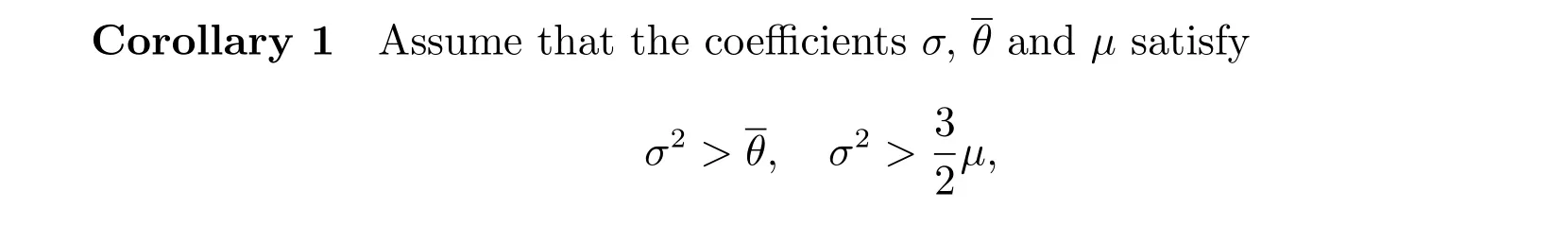
then the full discrete matrix I+ΔτS in (??) is anH+-matrix.
Remark 1 From the proof of Theorem 1, it is worth noting that both S and I+ΔτS areM-matrices under the assumption(??),which implies that the fully discretized system (??) satisfies the discrete maximum principle and thus the above discretization is monotone. This guarantees that an important property in option pricing theory,i.e.,the discrete arbitrage inequality holds.
The monotonicity of the fully implicit scheme(??)is given in the following theorem.

2.3 Linear complementarity problem
In (??), we let
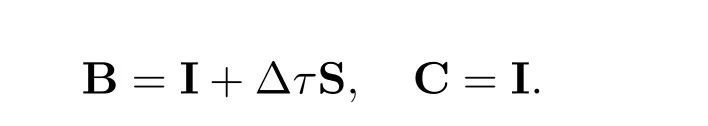
Then the space and time discretization of the American bond option model (??) leads

where the early exercise constraints are set to be zero instead of the payofffunction.For convenience, (??) is abbreviated as LCP(q,A).
A number of efficient iteration methods have been proposed for solving LCP, for instance, penalty methods[?], multisplitting iteration methods[?], projected relaxation methods[?]and modulus-based matrix splitting iteration methods[?]. In this paper,we apply the modulus-based successive overrelaxation and accelerated overrelaxation iteration methods developed in [?] for the solution of the LCP(q,A) (??).
3 Modulus-based matrix splitting iteration method
In this section, for the solutions of the LCPs coming from the finite volume discretization of American bond options (??), we discuss an efficient numerical method in detail, i.e., the modulus-based matrix splitting iteration method. The following theorem implies that the LCP(q,A) (??) is equivalent to a fixed-point problem.
Theorem 4[?]LetA=M-Nbe a splitting of the matrixA ∈Rn×n,Ω1andΩ2ben×nnonnegative diagonal matrices, andΩandΓben×npositive diagonal matrices such thatΩ=Ω1+Ω2. For the LCP(q,A), the following statements hold:
1) If (w,z) is a solution of LCP(q,A), thenx= (Γ-1z-Ω-1w)/2 satisfies the implicit fixed-point equation

is a solution of the LCP(q,A).

Now, the MSOR and MAOR algorithms are described as follows.
Algorithm 1 MSOR method

1.Choose x, Ω, α, tol, maxit;2.For it=1,2,··· ,maxit 3.z =|x|+x;4.b=[(1-α)D+αU]x+(Ω-αA)|x|-αq;5.Res=‖min(Az+q,z)‖2;6.If Res <tol 7.break;8.End 9.Solve (D+Ω-αL)x=b;10.End For
Algorithm 2 MAOR method

1.Choose x, Ω, α, β, tol, maxit;2.For it=1,2,··· ,maxit 3.z =|x|+x;4.b=[(1-α)D+(α-β)L+αU]x+(Ω-αA)|x|-αq;5.Res=‖min(Az+q,z)‖2;6.If Res <tol 7.break;8.End 9.Solve (D+Ω-βL)x=b;10.End For
Convergence conditions for the MSOR and MAOR methods are provided in the following theorem when the system matrix is anH+-matrix.


4 Numerical experiments
In this section, we present some numerical results to demonstrate the performance and convergence of the new numerical method.
For a fair comparison of different methods, in all the following experiments, the stopping criterion is
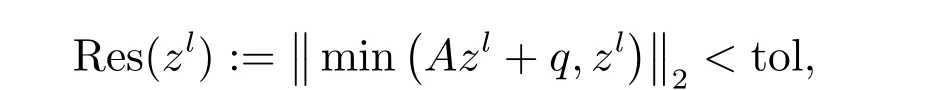

Then, the numerical order of convergence is defined by
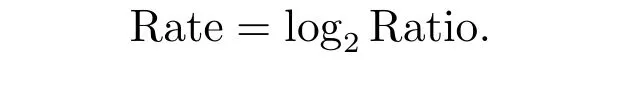
Further, for comparison, we also consider the projected successive overrelaxation iterative method(PSOR)[?]and penalty method for LCP,which the relaxation factorωin PSOR is chosen by minimizing the number of iteration steps,and the penalty method approach along with the fully implicit finite volume scheme to (??) is as follows
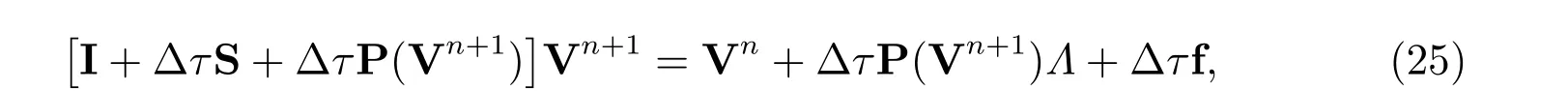
forn= 0,1,··· ,N-1, with V0being the given initial conditionΛ, P(Vn+1) is a(J-1)×(J-1) diagonal matrix with
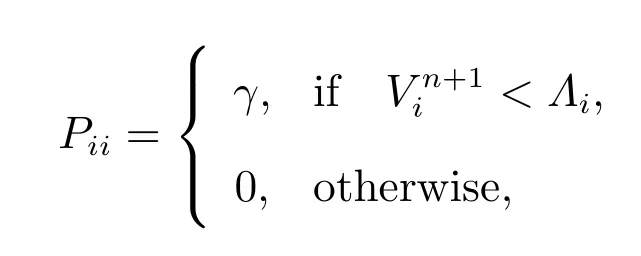
whereγis the penalty parameter.
Following[?,?],to solve the nonlinear algebraic system(??)effectively,we propose an iterative method at each time step as follows.
Algorithm 3 Iterative method for the numerical scheme (??)

1. Let n=0.2. Set l=0, ^V0 =Vn.3. Solve[I+ΔτS+ΔτP(^Vl)]^Vl+1 =Vn+ΔτP(^Vl)Λ+ΔτF,|^Vl+1 4. If max i -^Vl i|i |) <tolerance, then stop; Else l:=l+1 and go to Step 3.5. Set Vn+1 = ^Vl,n=n+1 and go to Step 2.1≤i≤J-1 max(1,|^Vl+1
In numerical experiments,the penalty parameterγand the tolerance are set to 104and 10-8in Algorithm 3, respectively. All codes were carried out in Matlab R2015b with 32.00 GB RAM and 3.20 GHz processor.
4.1 American vanilla put option
We present numerical results for American put option on zero-coupon bond with the corresponding parameters[?,?,?,?]

Figure 1 displays the time evolution and the optimal exercise boundaries of the American vanilla put options with different values ofσandR, wheremandnare the respective number of grid steps in ther-direction andτ-direction. And the corresponding Greeks(Delta and Gamma)atτ=Tare displayed in Figure 2. The stability of the proposed method are evident in these figures. Further, the convergence performance of the PSOR, MSOR, MAOR and penalty methods for the LCP resulting from the finite volume discretization are compared. As the analytical solution is unavailable, by using the fully implicit finite volume scheme and the MSOR method, we compute the reference numerical solution based on a fine grid with (m,n)=(6 400,3 200) asR=2 and(m,n) = (4 800,4 800) asR= 3, respectively. Then, the number of average iteration steps (denoted by ‘IT’), elapsed CPU time in seconds (denoted by ‘CPU’) and the relative error (denoted by ‘Error’) are listed in Tables 1~4 with differentσandR. From these tables, we can observe that the accuracy of the numerical solution of the LCP improves as the discretisation grid is refined. Although there are more iteration steps for the MSOR and MAOR methods than the PSOR method, the MSOR and MAOR methods require less CPU time than PSOR and penalty methods, while the MAOR method requires the least CPU time. Finally, Tables 5 and 6 contain the computed ratios by the four methods with differentσandR. From the results in these two tables,we can see that the order of convergence of the fully implicit finite volume scheme is roughly 1 in the discrete maximum norm. This is consistent with the properties of the implicit scheme.
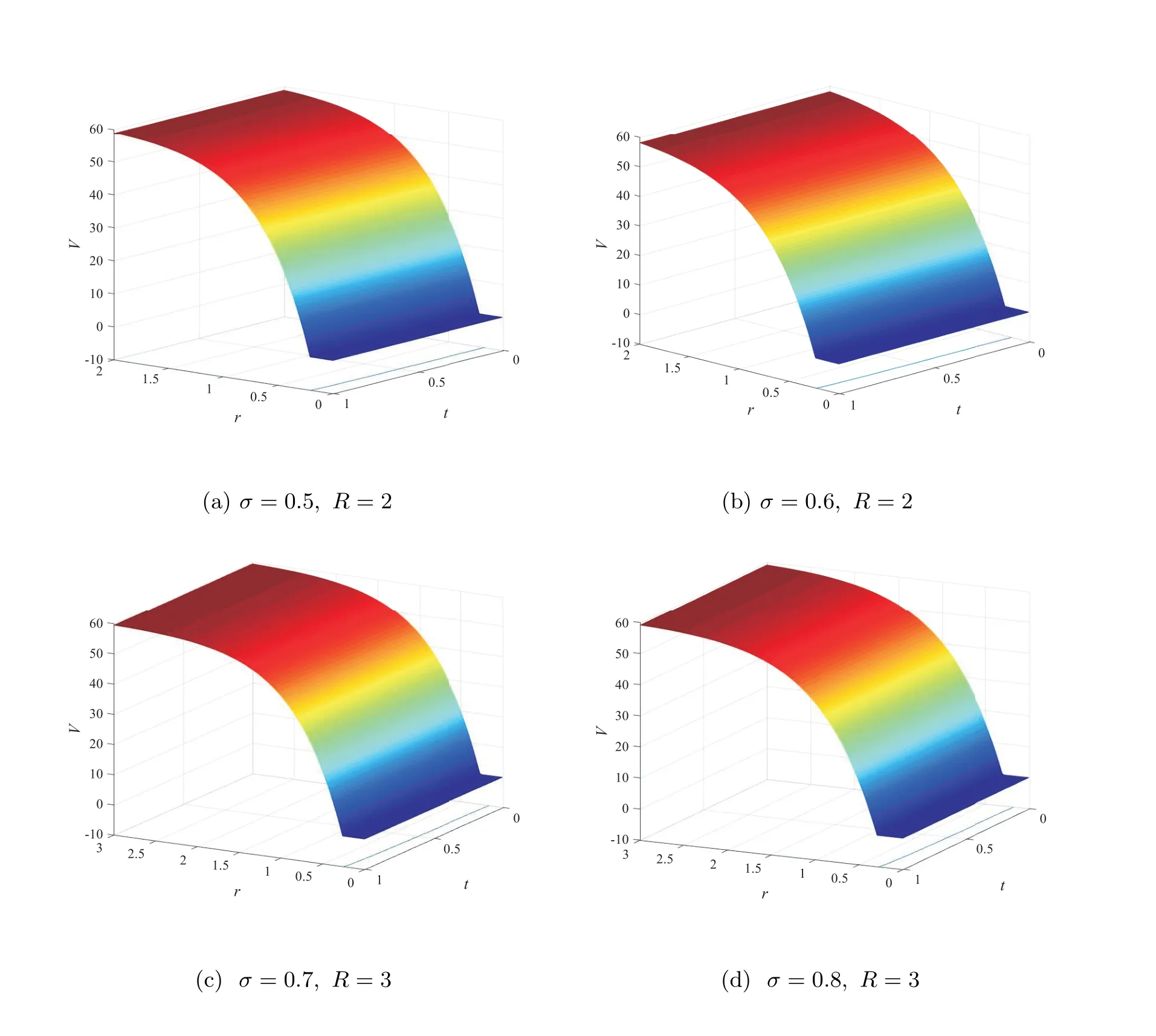
Figure 1 Surface plots and the optimal exercise boundaries of the American vanilla put option on a zero-coupon bond based on (m,n)=(800,400), using the fully implicit finite volume scheme combined with the MSOR method
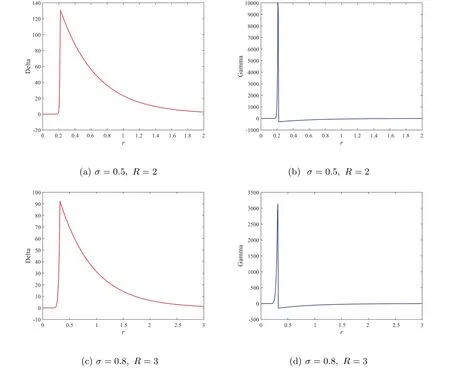
Figure 2 Delta and Gamma values of the American vanilla put option on a zero-coupon bond based on (m,n)=(400,200), using the fully implicit finite volume scheme combined with the MSOR method
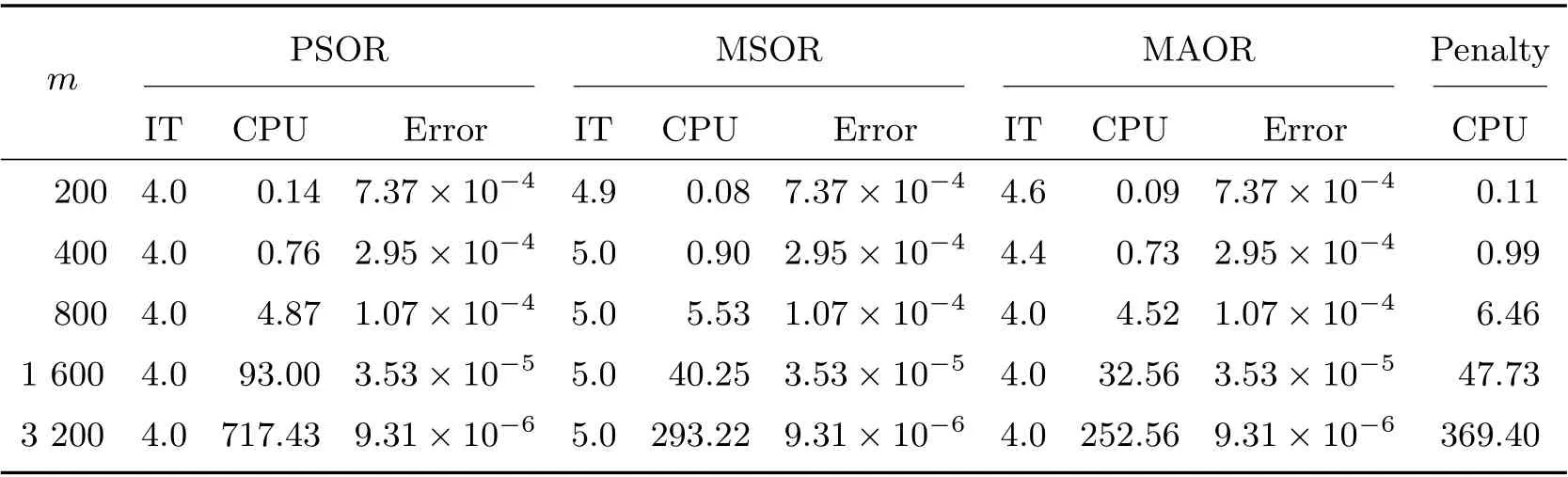
Table 1 Comparison of four methods on different grids with σ =0.5 and R=2 when m=2n
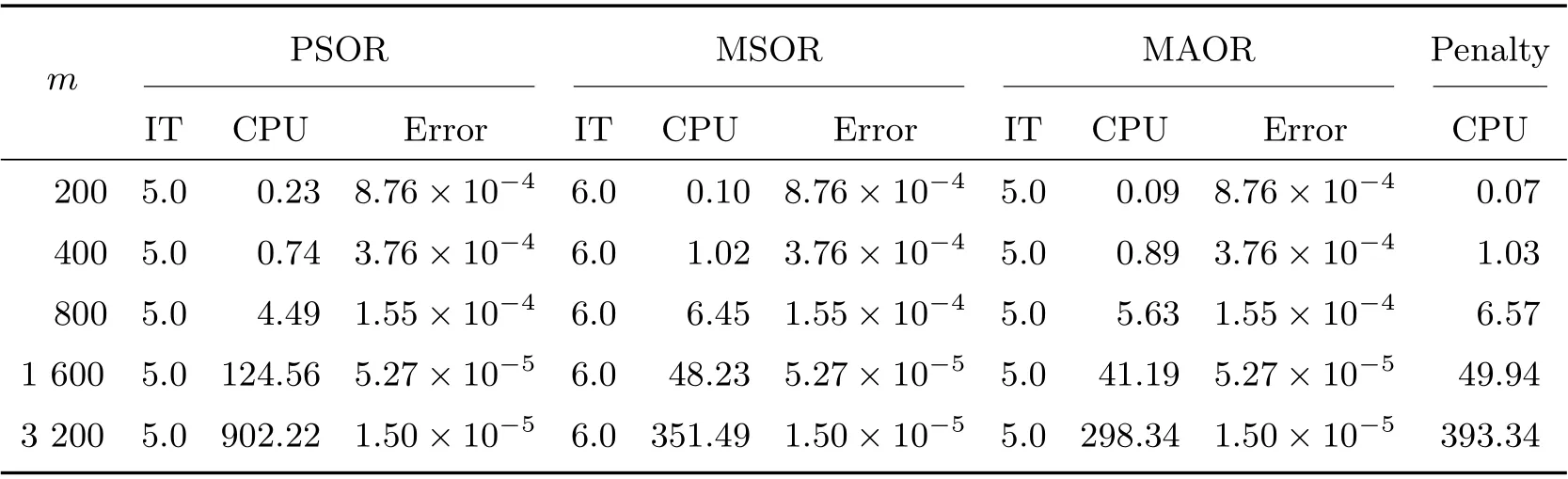
Table 2 Comparison of four methods on different grids with σ =0.6 and R=2 when m=2n
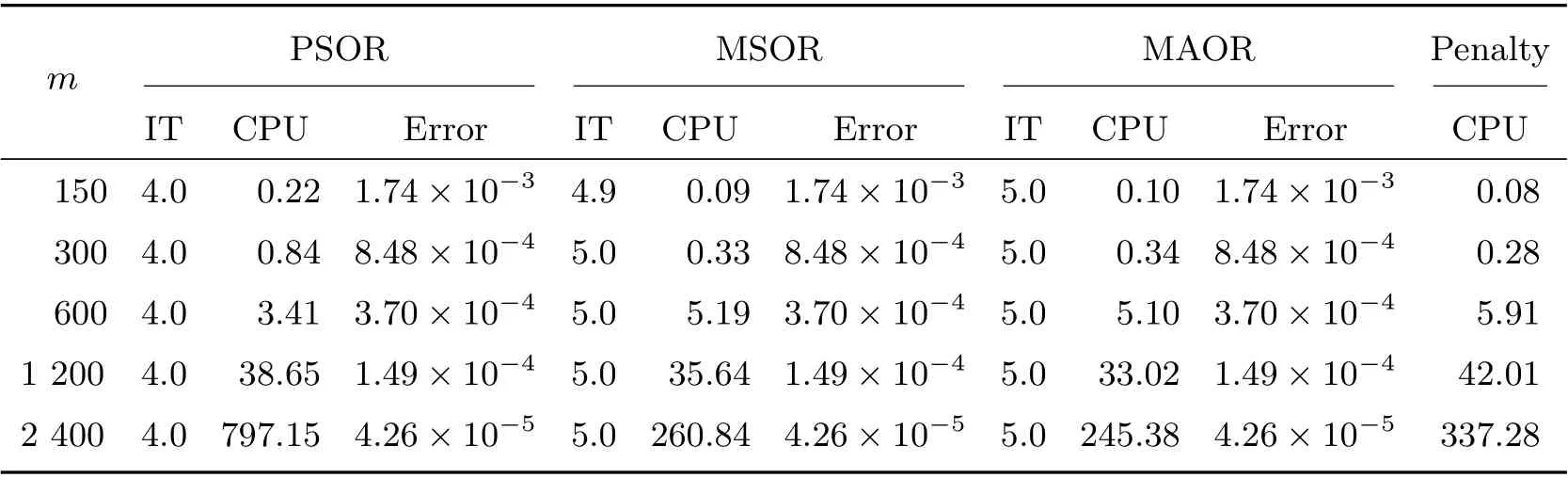
Table 3 Comparison of four methods on different grids with σ =0.7 and R=3 when m=n

Table 4 Comparison of four methods on different grids with σ =0.8 and R=3 when m=n

Table 5 Rates of convergence with σ =0.5 and R=2 when m=2n
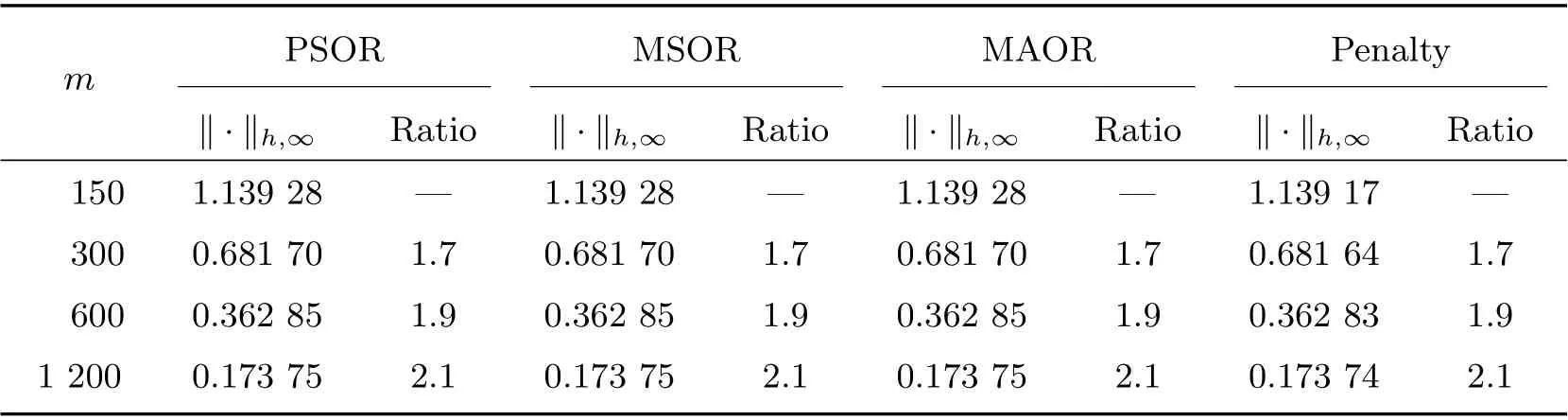
Table 6 Rates of convergence with σ =0.8 and R=3 when m=n
4.2 American digital option
We assume that American digital option has the discontinuous payoff

In Figure 3, we plot the option value surface, the option value, Delta and Gamma values atτ=T. Obviously,these figures show that the numerical solutions contains no oscillations which implies our method is robust. We also can observe that the MSOR and MAOR methods require less CPU time than the PSOR and penalty methods, and the MAOR method requires the least CPU time in these four numerical methods for LCP from Figure 4. Hence, we should remark that the finite volume method combined with the MAOR method will be very effective for pricing American bond options.
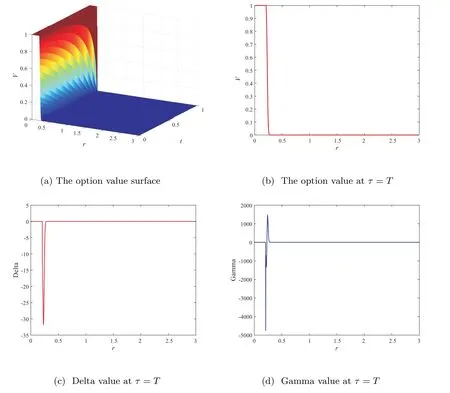
Figure 3 American digital option on a zero-coupon bond based on (m,n)=(1 200,1 200), using the fully implicit finite volume scheme combined with the MSOR method

Figure 4 The elapsed CPU time of four methods when m=n
5 Conclusion
In this paper,we developed a class of finite volume method for the spatial discretization of the PDE arising from pricing American put option on a zero-coupon bond. The method is coupled with a fully implicit time-stepping scheme. We have shown that the discrete matrix is anH+-matrix under some parameters assumption, and the discretization scheme is stable and monotonic. Due to the early exercise constraint of the American bond options pricing, the modulus-based matrix splitting iteration method has been used to solve the resulting LCPs, and an associated convergence theorem has been established as well. Finally,numerical experiments were performed to demonstrate the convergence, efficiency and usefulness of the new method.
