多因素耦合影响亚音速喷口强化气体流场分布研究

2021-04-26崔骊水李春辉

计量学报 2021年3期

张翰，贾力，崔骊水，李春辉

(1.北京交通大学，北京 100044；2.中国计量科学研究院，北京 100029)

1 引言

气体流量作为机电系统与设备的关键过程参数，其测量准确性直接决定着系统与设备驱动控制的有效实现、性能指标的可靠评价和结构动力的科学优化，而这离不开气体流量测量的支持[1,2]。传统测量方法主要依赖于不同原理的气体流量计得以实现，但是其测量能力易受到工况的限制；而基于均匀流场的速度面积法对此显然更具优势[3]。例如，航空发动机具有工况复杂、进气流量大且性能苛刻等特点，作为其推力优化基础的空气进气量主要依靠速度面积法测量获得，而测量流场的均匀性直接影响着测量水平[4]。同时，基于均匀流场的速度面积法在高压天然气流量测量、温室气体及大气污染物排放量监测等具体应用中均发挥着重要的作用[5，6]。

均匀流场主要具备两个特点：均匀区域占比与均匀性，二者共同决定了流场分布的品质，并且容易受到管路条件与实际工况的影响。圆形亚音速喷口作为典型的气体射流上游结构，可以提供具有较高核心区占比的均匀流场(top-hat流场)，被广泛应用于均匀流场的构造[7]。

Mi等[8]研究了孔口强化流场分布并提出收缩断面效应(Vena contracta effect)是流场强化的主要原因。与孔口结构不同，亚音速喷口具有更长的内部流动距离，收缩断面效应明显不适用。Quinn等[9]通过实验比较了亚音速喷口与孔口强化流场分布的不同，并提出二者强化作用的机制并不相同；同时，亚音速喷口强化流场的核心区也可以观察到一定的马鞍型特征，即实际核心区域存在一定速度梯度[10]。

Chen[11]对矩形亚音速喷口强化流场分布进行数值模拟研究，发现方形横截面的4个顶点对气体流体产生应力集中作用，使得流体形成二次流与主流发生叠加，从而引起流场分布改变；Zhang等[12]对圆形亚音速喷口强化气体流场进行数值模拟研究，发现喷口内沿程压力梯度分布不均匀是流场强化的根本原因；在此基础上，部分学者发现流动工况直接影响强化流场分布核心区占比与马鞍型特征。

虽然圆形亚音速喷口强化气体流场分布的作用机制已经明确，但是包括气体压力、流速以及收缩比在内的多因素耦合影响强化流场品质还有待进一步定量研究。特别是压力耦合影响下的边界层流场变化直接影响着速度面积法的测量范围。本文在压力-流速-收缩比等多因素耦合条件下，通过定义top-hat流场分布关键参数的方式，定量研究了压力与流速及收缩比对亚音速喷口强化气体流场分布的影响，并分析其具体作用规律，以期为复杂工况下基于圆形亚音速喷口的气体均匀流场构造提供参考。

2 亚音速喷口强化气体流动模型

选取任一过中心的横截面作为研究区域，建立流动方程组。如图1所示，假定圆形亚音速喷口内气体为定常、不可压缩流动，基于连续性方程与动量守恒方程，横截面上平均压力p由式(1)确定[13]：

图1 亚音速喷口强化气体流场分布过程示意图Fig.1 Schematic diagram of the development of gas flow field in the subsonic nozzle

(1)

式中：ur*为气体流速u在极轴r*分量；ν为气体流体的运动粘度；C为常系数。喷口内压力梯度∂p/∂r沿流动方向为非均匀变化，即为弯月面分布，这是流动强化的主要原因[12]。压力梯度与流体密度ρ、来流状态ur*、极轴r*直接相关，分别对应压力p、流速u与收缩比RA，且每个因素的权重并不一致。

3 强化流场分布的定量评价方法

亚音速喷口强化后气体流场分布如图2所示，核心区流场是其均匀区域的主要载体，而流场核心区存在的马鞍型特征又使得实际流场与理想流场存在一定差异，降低了强化流场的均匀性。因此，本文针对亚音速喷口内流场分布的典型特征，提炼关键量化参数为核心区占比与核心区马鞍型特征的定量评价提供依据，并研究压力-流速-收缩比的耦合影响。

图2 亚音速喷口强化后气体流场分布(理想与实际流场)Fig.2 Gas flow field generated by the round subsonic nozzle (ideal and actual flow field)

① 核心区占比Rc

核心区占比是均匀流场的主要特征，直接关系均匀流场区域范围，其计算式为：

(2)

式中：rcore为核心区流场半径；r为流动横截面半径。

② 鞍背度Δpc、鞍背方差σ(Δpc)

Chen[11]等定义鞍背差值表征核心区马鞍型特征，但是如果速度奇点存在于核心区内，鞍背差值则不能准确表征上述特征。由此,本文定义鞍背度与鞍背方差共同表征真实核心区流场分布偏离理想分布的程度，计算式为：

(3)

(4)

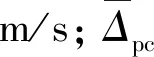
实际上，亚音速喷口内流场演化是由于通道内沿程压力梯度分布的不一致所引起，而多因素耦合影响也是通过对强化过程的作用得以完成。因此，本文把近壁面与中心处压力梯度相等位置定义为压力梯度平衡点，与文献[12]定义的临界位置点共同定量表征多因素耦合影响的强化过程。

4 数值计算方法

4.1 网格划分

为了保证数值模拟有效性，所用几何模型与实验段组成一致，计算域由亚音速喷口与下游结构组成[12]。同时，入口段与出口段分别向两侧延长12D和20D，这样不仅保证来流气体的流动状态与实验状态相近，还可以有效避免下游长度不足引起的回流影响。图3为示意图，图中xy截面与实际结构不成比例。

图3 亚音速喷口强化气体流场分布计算域Fig.3 Calculation domain of the gas flow field in the subsonic nozzle

基于ICEM采用六面体结构化三维网格划分几何模型，根据流场变化程度及关注区域对网格进行局部加密和调整，特别是靠近壁面处区域。在保证计算有效的基础上，尽量降低网格密度。

4.2 计算设置

基于FLUENT 19.2进行求解，求解器为基于压力的隐式稳态求解器；压力与速度的耦合求解通过SIMPLEC算法实现，对流项离散使用QUICK格式；湍动能和湍流耗散率为二阶迎风差分格式；计算停止判据采用速度残差低于10-8和出口质量流量保持稳定；湍流模型为标准k-ε模型[12]；气体密度由理想气体状态方程获得,边界条件基于实验工况设置,入口条件为速度入口，出口则为自由流出口。

计算工况见表1，主要考虑：一是与实验系统的能力相匹配，计算的基础管道流速范围为0.11～5.57 m/s；二是与应用工况相匹配，DN 200的流量计上限一般在1 000 m3/h左右，对应管道流速8.84 m/s，因而管道流速上限拓展至9 m/s左右。表中，upipe为管道中心流速，uc为喷口出口处中心流速。

表1 亚音速喷口强化气体流动数值计算工况Tab.1 Calculation conditions of gas flow in subsonic nozzle

4.3 网格独立性验证

基于收缩比为9的几何模型进行网格独立性验证。图4所示3模型计算结果均能满足计算要求，标准k-ε模型表现更优。500万网格数以上，出口质量流量不再随网格数的变化而改变。本文网格划分选用500万网格数的参数值，所有的模型网格数位于(500～600)×104之间，具体数目存在一定差异。

图4 不同网格数亚音速喷口出口质量流量Fig.4 Outlet mass flow of different grid numbers

5 结果与讨论

5.1 实验验证模拟有效性

数值计算的有效性基于负压法实验系统进行实验验证，通过比较喷口出口处气体流场分布完成[14]。验证工况为0.1 MPa和1 MPa下各选取高低2个流速点，尽可能地覆盖实验系统的实际能力以及数值计算的工况范围，结果如图5所示。

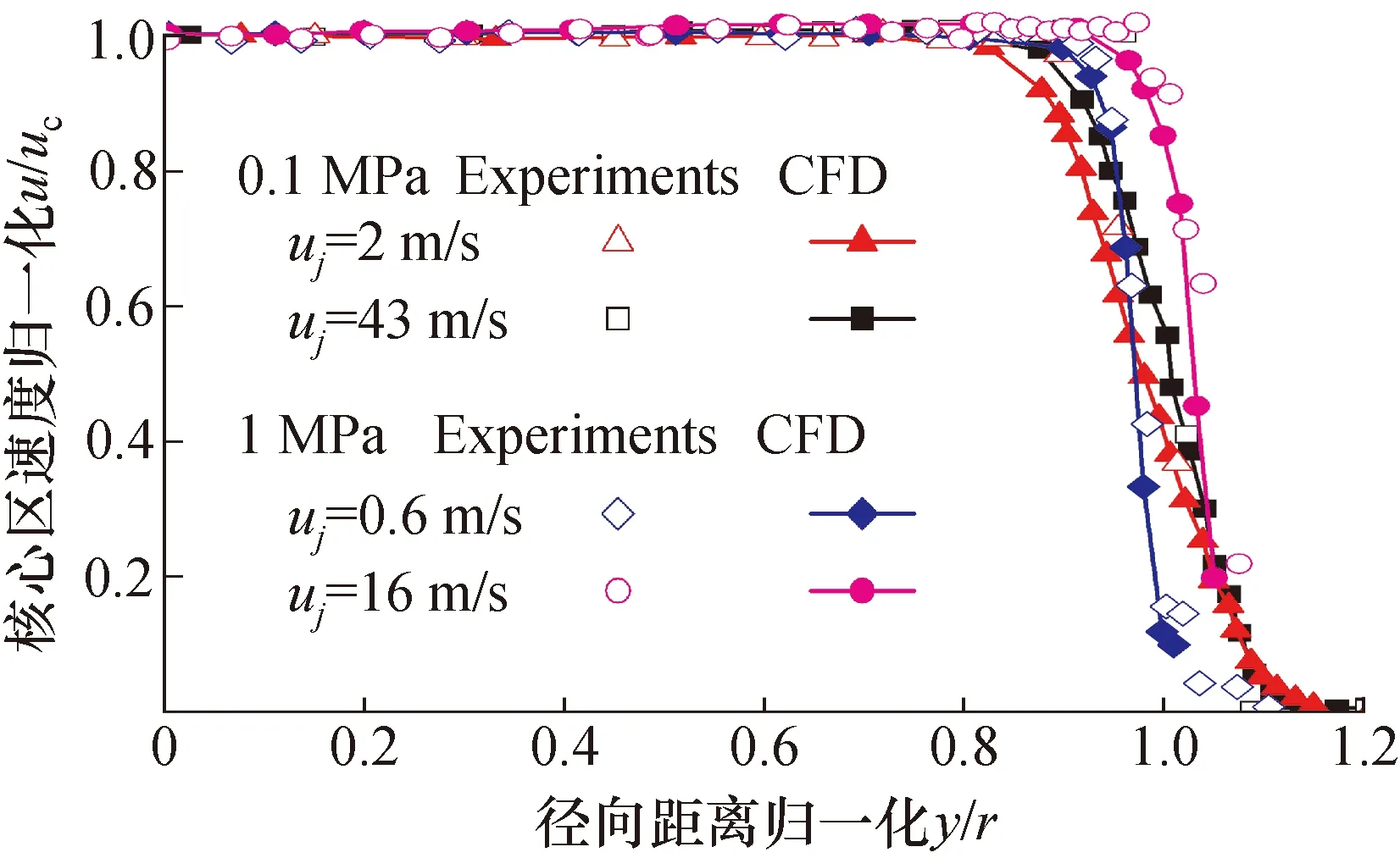
图5 实验与CFD结果的速度分布验证Fig.5 Validation of the velocity profile between experimental data and CFD results

结果表明数值模拟的计算结果与实验测量分布一致性较好，二者均呈现帽顶型流场分布。数值计算的难点依然在边界层区域。由于实验系统所提供的喷口出口最大中心速度为21 m/s左右，且最大压力为1 MPa，本文仅对该压力与速度范围内的数值计算进行了验证。然而，这并不意味着更高压力与速度下数值计算的有效性得不到验证，实际上，边界层的影响随着速度和压力的增加而不断减小。因此，基于该数值计算可以为进一步分析讨论提供支撑。

5.2 压力-流速影响

压力-流速对亚音速喷口强化气体流场分布的影响见图6所示，其中Ls为亚音速喷口的长度。由图可以发现随着流动距离的增加，喷口内气体流场分布逐渐向帽顶型分布演变，并且受到压力-流速共同影响。现有研究表明流速增加会使得绝对压力梯度增加，进而促进强化流场分布的形成。相同流速下，压力的增加可以有效降低边界层占比，并且压力对边界层的影响随着流速的增加减弱。

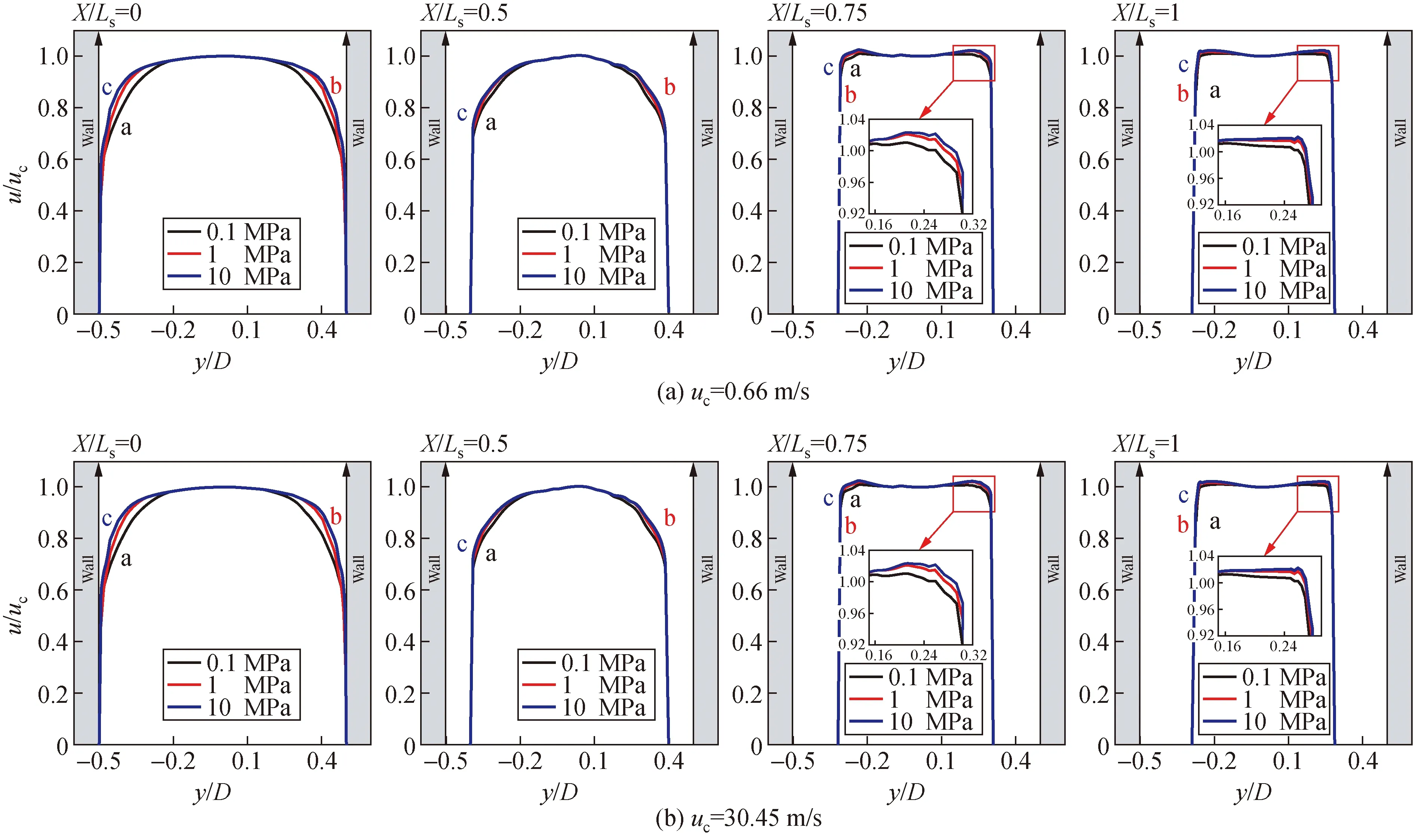
图6 压力-流速对强化流场分布的影响Fig.6 Influence of pressure and inlet velocity on flow field of gas flow in subsonic nozzle

出口速度为0.66 m/s时，压力从0.1 MPa增加到10 MPa所引起的边界层厚度变化约为0.15D，而出口速度为30.45 m/s时仅为0.05D。相同流速下，压力的增加可以改变核心区流场的鞍背度，使得强化流场偏离理想流场分布。

图7为压力-流速对临界点位置的影响。流速的增加虽不会明显改变临界点的位置，但临界点的位置会随着流速的增加在一定范围内波动；而压力的增加会有效缩减波动的范围，进一步减小速度的增加对临界点位置的影响。当压力为0.1 MPa时，出口流速从0.6 m/s增加到94.8 m/s，临界点位置在0.66L到0.7L之间变化；压力增加到10 MPa时，特别是1 MPa后，随着流速的增加，临界点位置的变化范围已经缩减至0.65L到0.67L之间。因此，压力的增加虽然不会改变喷口内压力梯度的分布趋势，影响强化进程，但是压力的增加会进一步提升压力梯度分布的稳定性，降低流速对强化过程的影响。特别是对于低流速下的强化过程，临界点的位置会随着压力的增加而略向喷口上游移动。

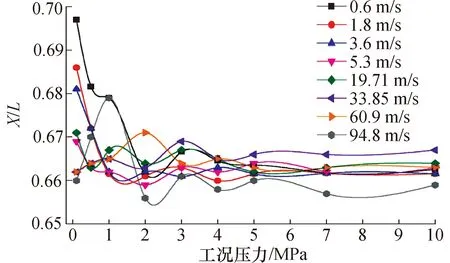
图7 压力-流速对临界点位置的影响Fig.7 Influence of pressure-inlet velocity on critical position

图8为压力-流速对压力梯度平衡点的影响。流动横截面中心处与近壁面处压力梯度曲线交点位置即两梯度值相等时为压力梯度平衡点，按沿程顺序先后依次为第一压力梯度平衡点与第二压力梯度平衡点。压力与流速的增加并不会显著影响临界点的位置，这也说明第一压力梯度平衡点也不会明显受到压力与流速的影响。图8(a)为不同压力与来流速度下，第一压力梯度平衡点的位置主要位于0.52L～0.55L之间；但是当在工况压力小于1 MPa、出口中心速度为0.6 m/s时，第一压力梯度平衡点的位置显著高于该区间，达到0.64L。这说明流速对喷口内压力梯度的影响随着压力和流速的增加而逐渐减弱，但低压力低流速下，强化过程更易受到压力与流速的影响。

与临界位置点和第一压力梯度平衡点不同，压力与流速对第二压力梯度平衡点的影响更为明显，见图8(b)所示。由图可以发现，不同流速下，随压力的增加第二压力梯度平衡点位置的分散性明显增大，压力的增加会使得压力梯度分布更加趋于一致，但是流体离开喷口后会存在膨胀做功，喷口出口附近压力变化不均匀，并且与压力和来流速度有关。在现有研究中，已经发现喷口出口附近会随着工况的不同而出现不同的压力梯度分布。

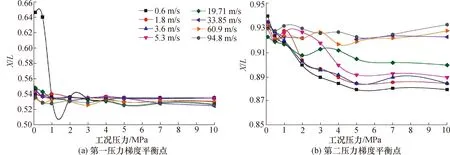
图8 压力-流速对压力梯度平衡点的影响Fig.8 Influence of pressure and inlet velocity on pressure gradient balance point

此外，高压力大流速下，第一压力梯度平衡点与临界点位置保持稳定，但是第二压力梯度平衡点的位置却略微靠近喷口出口，这有效缩减了发展阶段的沿程长度，会导致高压力大流速下流场核心区占比的增加和鞍背度的增大，见图9所示。强化流场的核心区占比依然先平稳后增大随后再缓慢变化。压力与来流速度的增加均会使得强核心区占比的提升，但是发展阶段的存在会使得核心区占比出现一定程度的下降；同时，核心区流场鞍背度沿流动距离呈现“Λ”型分布，且随着压力和流速的增加而明显变大。

图9 压力-流速对强化流场品质的影响Fig.9 Influence of pressure and inlet velocity on quality of velocity profile in subsonic nozzle

5.3 压力-收缩比影响

改变喷口出口直径，使得所研究的喷口收缩比

可以从3增加到11。压力-收缩比对亚音速喷口强化气体流场分布的影响见图10所示。

图10 压力-收缩比对临界点位置的影响Fig.10 Influence of pressure and contraction ratio on critical position in subsonic nozzle

在相同的工况压力与相近的流速范围下，具有高收缩比的亚音速喷口通道，其临界点的位置越靠近下游出口。归因于收缩比的增加，引起了第一压力梯度平衡点向喷口下游移动，带动了强化阶段随之移动，而压力梯度分布绝对值的增加，使得临界点在该区域更快地出现。因此，高压力高收缩比下的临界点位置位于低压力低收缩比的下游，这有利于强化流场的核心区占比的增加，但同时也会带来更为明显的马鞍型特征。此外，不同压力与流速下临界点位置的一致性随收缩比增加而提高。

不同流速下，压力-收缩比对核心区占比的影响见图11所示。与收缩比为3相比，收缩比为7和11的强化流场核心区占比更高，并且强化阶段内核心区流场占比陡然增加的区域明显向下游移动。随着压力和流速的增加，收缩比为3的喷口强化流场核心区占比最大值为85%左右，而收缩比为7和11的喷口强化流场下最大值则可以超过90%。因此，高收缩比通道下的设计可以提高强化流场的核心区占比。然而，强化流场核心区占比的最大值依然位于0.8L～0.9L区间内的发展阶段，在此之后占比出现不同程度的明显下降。这说明虽然通过压力-收缩比-流速的增加可以提高强化流场的品质，但是发展阶段会恶化强化效果。

图11 压力-收缩比对强化流场核心区占比的影响Fig.11 Influence of pressure and contraction ratio on core flow ratio in subsonic nozzle

图12为不同流速下，压力-收缩比对鞍背度的影响。

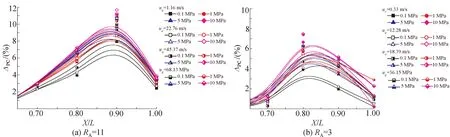
图12 压力-收缩比对强化流场鞍背度的影响Fig.12 Influence of pressure and contraction on correction peak-center difference in subsonic nozzle

高压力、高收缩比下的强化流场的确出现了更高的鞍背度，强化流场核心区的马鞍型的特征更为明显。当收缩比为11时，鞍背度的最大值接近于12%，此时工况压力为10 MPa；当收缩比为3时，最大值则减小到7.5%左右，此时工况压力也为10 MPa；同时，压力和收缩的增加还使得鞍背度最大值出现位置靠近喷口出口，收缩比由3增加到11时，极值点位置相应的移动了0.1L左右。