基于分数阶傅里叶变换的NURBS曲面拟合

孔德明，黄紫双，王书涛，史慧超

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.北京化工大学 信息科学与技术学院，北京 100029)

1 引 言

当前现代化工业不断发展，机械加工市场规模不断扩大，各种形状的零件被加工和生产出来，自由曲面模型重建在逆向工程与加工业中充当着重要角色，在产品的设计周期中，这种技术越来越重要[1]。随着工艺技术的提高，由自由曲面构建而成的物体广泛存在于人们的日常生活中，由于绝大多数自由曲面模型的外部形状无法用准确的解析函数表达式来描述，在对这类物体进行生产加工时，需要将这些曲面以几何参数模型的形式进行精确表示[2]。因此，在智能化现代加工工业中，设计人员会对这类物体的原始模型进行三维测量，得到其点云数据，然后对点云数据进行处理，对被测模型表面曲面上具有特征信息几何参数进行提取，并对被测模型曲面结构进行重建，也就是利用逆向工程技术实现对其进行设计并大批量高精度加工制造的目的[3]。

一般情况下，在逆向工程中曲面重构多采用传统的非均匀有理B样条(non-uniform rational B-splines,NURBS)曲面拟合方法[4]，通过对数据点插值生成拟合曲面，再利用最小二乘法修改输入数据项来逼近曲面的形状达到改善曲面精度的目的。该方法适用于任何曲面的拟合，但最小二乘法得到的拟合结果往往在间断和尖点处误差较大，曲面精度改善效果不佳。

为了解决此问题，张翠翠等[5]提出了一种对点云数据进行Delaunay三角剖分的曲面方法，通过三角域向矩形域的转换来完成各矩形区域的Coons曲面重构，进而插值Coons曲面得到光滑拼接的NURBS曲面，该方法将三角面重构与四边域曲面重构将结合，可用改善拟合曲面的光顺性，但在进行Delaunay三角剖分时，易产生局部大曲率部分划分效果差的问题，导致重构曲面拟合误差大，进而影响曲面重建结果；张娟等[6]提出一种基于中心减少的两层隐式函数插值算法，通过对插值得到的粗层曲面和表面点拟合得到的细层曲面求和得到整个重建表面，该方法实现曲面快速重建的同时保持曲面的真实性，但当点云数据较多时，无数次的插值和逼近导致较大的计算量，降低曲面重建效率。

近年来，有关学者尝试将借助小波变换时频分析对点云数据进行压缩和提取的方法应用到曲面重构中，取得了较好的效果[7,8]。本文提出一种基于分数阶傅里叶变换的NURBS曲面拟合方法，相比于传统的NURBS曲面拟合和小波分析方法，将传统的多分辨率时频域分析理论推广至时域中，其对波形信号中包含的复杂特征分量具有更好的解析效果，借助分数阶傅里叶变换对自由曲面结构点云数据的快速、高精度滤波、特征提取，进而对自由曲面进行NURBS拟合和形状优化，以得到自由曲面模型更高精度的重构曲面，减少曲面调整次数，简化曲面拟合过程。

2 本文方法

2.1 自由曲面结构的NURBS拟合

2.1.1 自由曲面结构表面特征提取

利用高精度三维扫描仪对复杂曲面模型进行扫描，获取自由曲面模型表面各点在XYZ三维空间内的位置信息形成点云数据。为了便于应用离散分数阶傅里叶变换[9]对其处理分析，通常将这些无序分布点云数据进行格网化处理。运用数据插值方法对高程数据进行插值处理，得到网格的高程值。将等间距网格作为一幅图像中的像素点，再将网格的高程值作为像素点所处位置的像素值，即获得自由曲面模型沿x轴方向的第i条高程序列Nyi和沿y轴方向的高程序列Nxi，高程序列上像素点的像素值即为各点在XYZ空间内的z轴坐标值。

分数阶傅里叶变换作为傅里叶变换的广义形式，随着变换阶数p从0连续增长到1，展示出信号从时域逐步变化到频域的所有特征[10]。

如图1所示，p阶分数阶傅里叶变换就是时频域旋转角度p(π/2)构成的新的(u,υ)域。利用离散分数阶傅里叶变换对自由曲面特征信息进行提取，可以将自由曲面沿x轴方向上的高程序列Nyi和沿y轴方向上的高程序列看作Nxi是由m组正弦波叠加组成的信号[11]，图1中高程序列上的横坐标方向编号为时域的时间轴，纵坐标的幅值即为高程序列上像素点的像素值。其分数阶傅里叶变换[12]为：

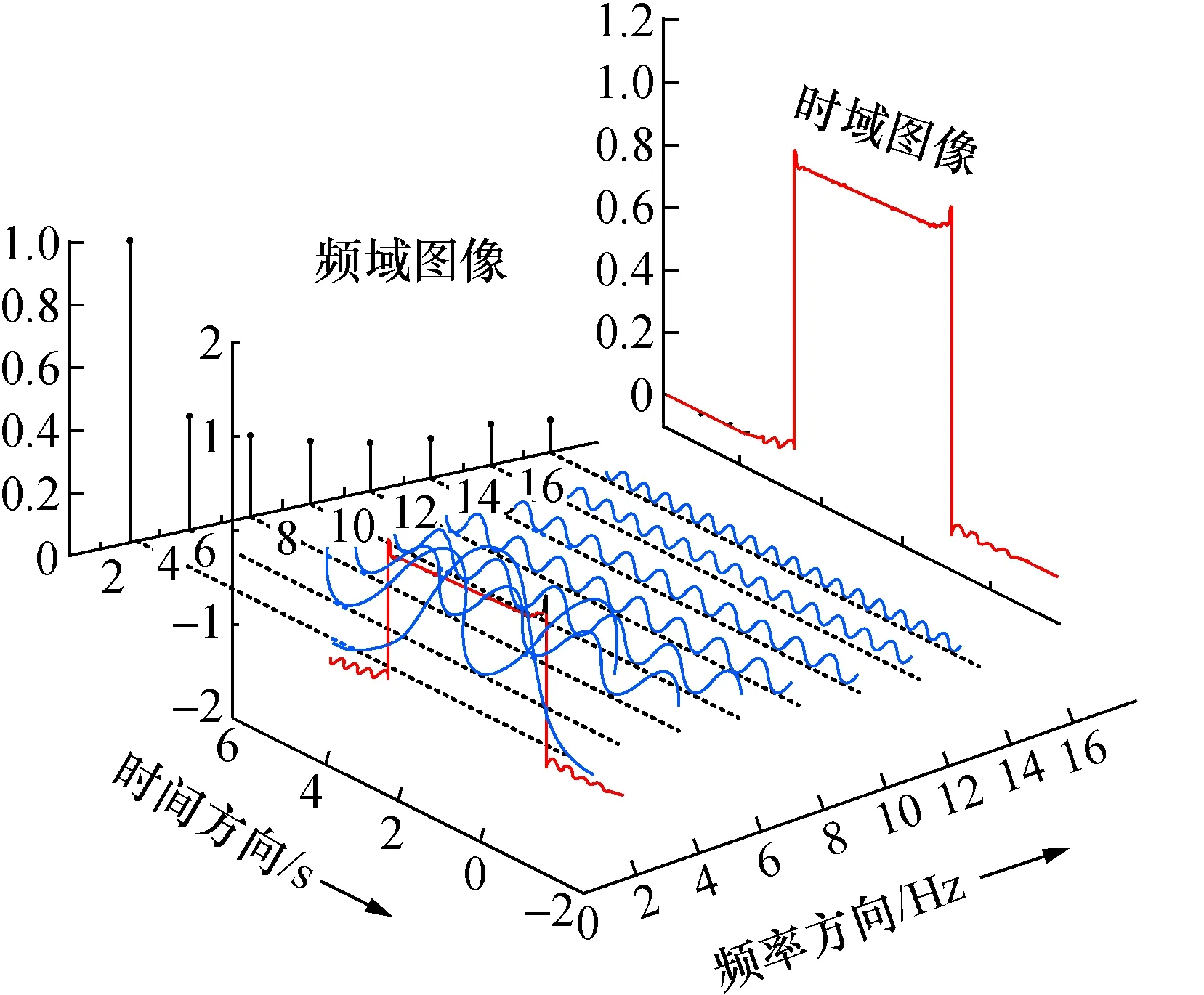
图1 时域和频域图像Fig.1 Image of time-domain and frequency-domain

(1)

(2)

式中：x(h,t)=[h1,h2,…,ht]是作为原始信号的高程序列；Kp1,p2(h,t,u,v)是分数阶傅里叶变换的核函数；α=p1·(π/2)，β=p2·(π/2)表示二维分数阶傅里叶变换的旋转角度。

由于分数阶傅里叶变换是线性变换[13]，根据其性质可知高程序列的特征信息包含于分数阶傅里叶变换序列中。为了更加准确地获取边缘和曲率的特征信息，按照式(3)求解高程序列的特征信息曲线，其中i代表第i条高程序列。

Hi=Hi(u,v)-Hi-1(u,v)

(3)

2.1.2 曲面拟合的数据点提取

由于拟合曲线的形状未知，仅通过得到的特征数据点的坐标数据信息不能确定两相邻特征数据点之间的单调曲线的形状，因此采用外切圆取点法在两相邻特征数据点之间的曲线上均匀选点，将直线看作曲线中的特例。外切圆取点法根据3个共面的点确定一个圆的特性，按照x轴从左到右的顺序选取3个相邻的数据点作外切圆。设定外切圆的一般方程式见式(4)，则圆心坐标为(D/2，E/2)。

(4)

然后，求得特征数据点Qi(xdi，zdi)到圆心的角度θi：

Δzdi=zdi-E/2，Δxdi=xdi-D/2

(5)

(6)

设定在每段曲线上选取n个点，则均匀选取数据点的圆心角度为

(7)

由式(5)得到的均分圆心角度求解均分直线的斜率：

kdi=tan(θi-nφi)

(8)

式中：kdi是第i个圆心角的角平分线斜率。

由于两相邻特征数据点之间的曲线方程未知，求解拟合曲线上的点到圆心的斜率：

(9)

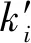
2.2 NURBS拟合曲面形状优化

将自由曲面模型和拟合曲面之间的差值序列作为被观测信号x(t)，利用离散分数阶傅里叶变换对信号进行旋转分离后信号表示[14]为

Xp(u)=Sp(u)+Np(u)

(10)

式中：Sp(u)为信号的分数阶傅里叶变换；Np(u)为噪声的分数阶傅里叶变换。

在u域上进行尖峰遮隔处理：

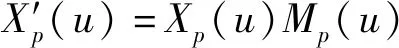
=Sp(u)Mp(u)+Np(u)Mp(u)

(11)

式中：Mp(u)是中心频率为u0的带通滤波器。

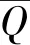
(12)

(13)

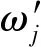
(14)

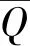
(15)

3 实 例

3.1 旋转自由曲面NURBS拟合

3.1.1 曲面表面特征提取

为验证本文方法的可行性，实验利用进口高精度3D打印机制作出一个旋转自由曲面结构的真实模型，模型加工精度为全曲面范围内±0.15 mm。使用德国生产的ATOS(V7.5)SR2扫描仪对加工获得的自由曲面模型进行扫描，得到真实旋转自由曲面的点云数据，如图2所示。

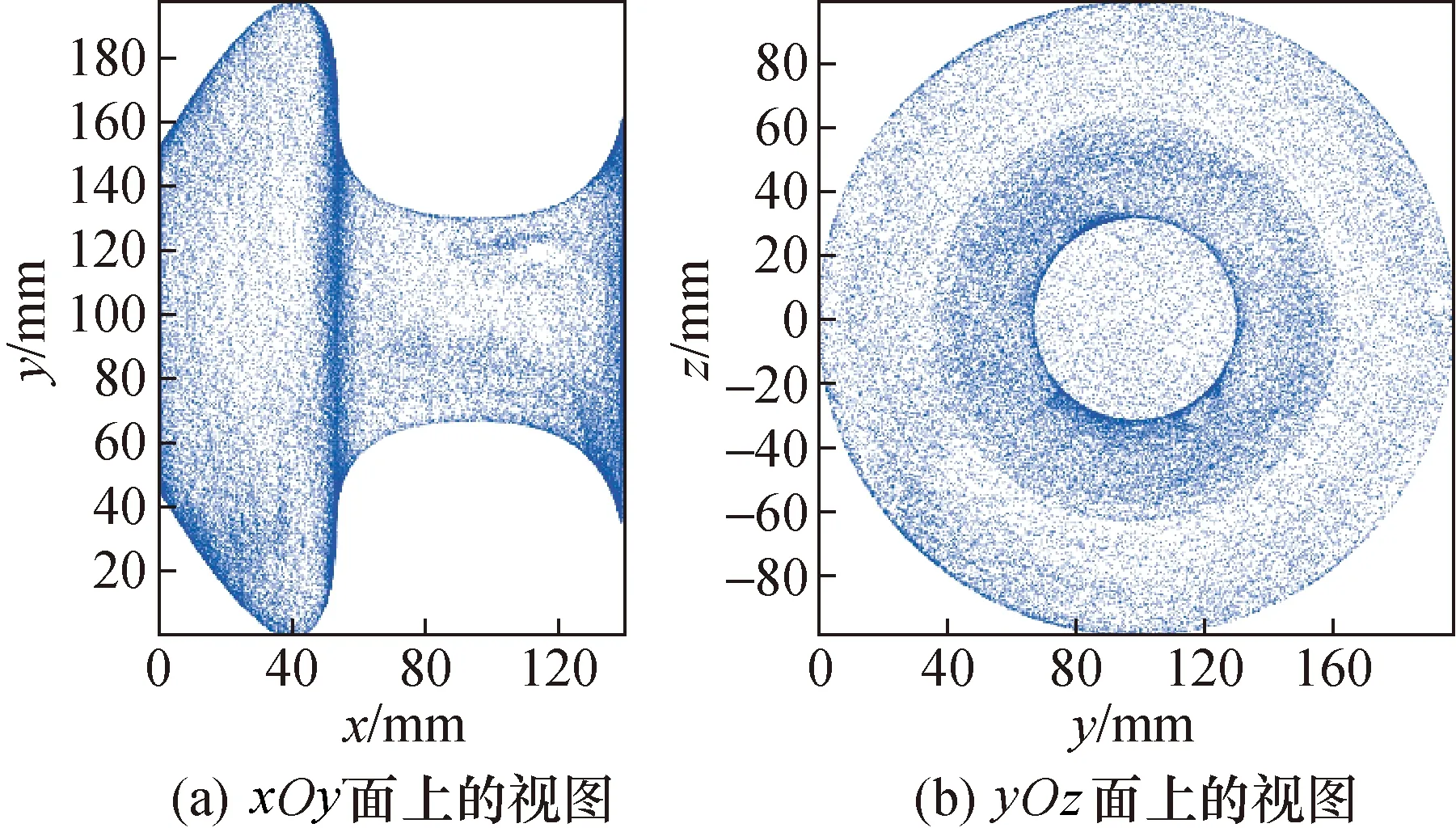
图2 旋转自由曲面点云数据Fig.2 Point cloud data of rotating free-form surface

对自由曲面的点云数据进行格网化处理获得其高程图像，计算各条沿x轴方向和沿y轴方向上被测模型表面结构的高程序列的高程值(即像素点的像素值)之和，计算得出沿x轴方向上被测模型表面结构的高程序列的序列值之和最大的序列为Ny109，沿y轴方向上高程序列的序列值之和最大的序列为Nx52，则被测模型表面最高点对应的像素点在xOy平面内的坐标为(52,109)，其示意图如图3所示，红色像素点对应的是Nx52高程序列，蓝色像素点对应的是Ny109高程序列。

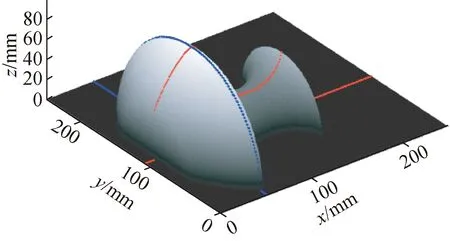
图3 旋转自由曲面的高程图像Fig.3 Elevation image of rotating free-form surface

根据旋转自由曲面最高点垂直对应旋转轴的特性，对得到的高程图像进行二维离散分数阶傅里叶变换，根据式(3)求解得到Nx52和Ny109高程序列对应的特征信息曲线来提取用于重构该旋转自由曲面的旋转轴和拟合曲线上的特征点，如图4所示。当特征曲线出现尖峰时，说明坐标编号对应的高程值发生突变，即该坐标编号对应的像素点位于旋转轴和拟合曲线的边缘位置或拟合曲线曲率较大的位置。图4(a)中，Ny109高程序列的特征曲线上有3个尖峰，对应的坐标编号为11、66和153，故该序列不关于旋转轴对称。图4(b)中，Nx52特征曲线尖峰对应的坐标编号分别为12和207，求解两坐标编号中间值为109，对应于高程图像最高点坐标。计算沿y轴方向上Nxi(i=1,2,3,…,153)高程序列的序列值之和，得到沿y轴方向上自由曲面的高程序列的序列值之和最小的序列为Nx109，则自由曲面的拟合曲线最低点对应的坐标编号为(109,109)。

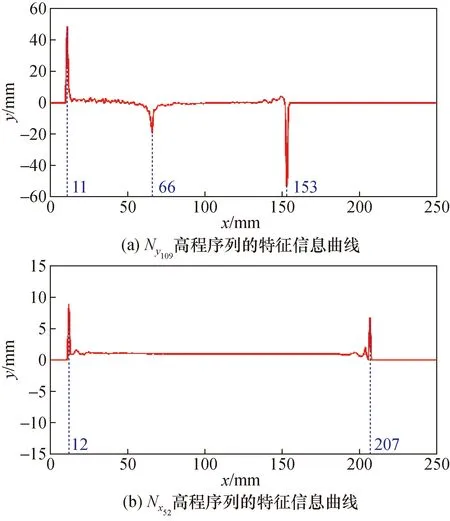
图4 高程序列对应的特征信息曲线Fig.4 Characteristic information curve of elevation sequence

综合上述求解出特征点对应的高程序列坐标编号，高程图像中这些坐标编号对应的像素点的高程值即为高，也是拟合曲线坐标数据中的z值。将拟合曲线左端边界点归于零点，由图4(b)解析可知自由曲面的旋转轴为y=98，选取Ny109高程序列作为用于拟合自由曲面模型NURBS曲面的拟合曲线，则选取的特征点Q1～Q5坐标数据如表1所示。

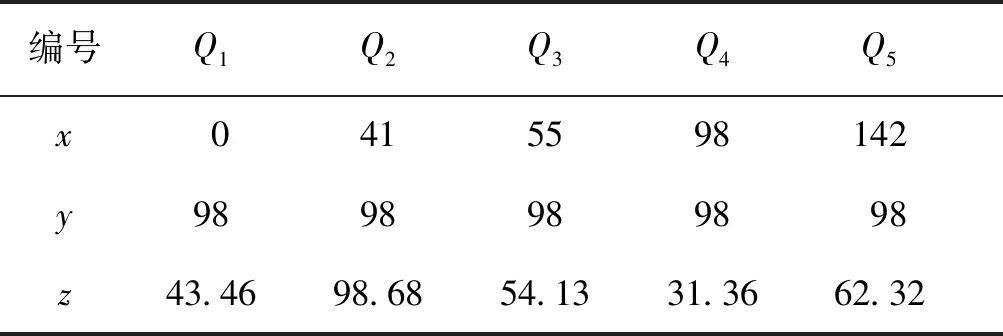
表1 特征点坐标数据Tab.1 Coordinate data of characteristic points mm

3.1.2 曲面表面数据点选取

结合表1中提取的5个特征数据点，利用外切圆取点法在两相邻特征点之间选取用于曲面拟合的数据点，其示意图如图5所示。

图5 自由曲面的数据点选取示意图Fig.5 Diagram of data points selection of free-form surface

按照x轴从左到右的顺序将特征点分为两组，相邻的3个特征点为一组。将两组特征点的坐标数据分别代入式(4)可求得两个外切圆的一般方程式系数为

(15)

从而求得两外切圆的圆心分别为O1(23.625,68.75)和O2(95.88,79.41)。将上述数据代入式(5)和式(6)中求得特征点到圆心的角度θi，

(16)

设定在每段曲线上选取n=1个点，则均匀选取数据点的圆心角度为

(17)

结合式(16)～式(17)中的角度值计算得到角均分线的斜率kdi

(18)

继续求解拟合曲线对应的高程序列上各像素点到圆心的斜率，选取与式(18)得到的斜率相近的像素点作为用于拟合的数据点，数据点位置见图5中三角形标记处，坐标数据见表2所示。

利用表1、表2中的数据点对自由曲面进行重建，得到的初始拟合曲面如图6所示，对其进行误差分析[18,19]，求解得到拟合曲面与点云模型之间的差值绝对值的平均值为1.386 8 mm，均方根误差为0.710 5 mm。

表2 数据点坐标数据Tab.2 Coordinate data of data points mm

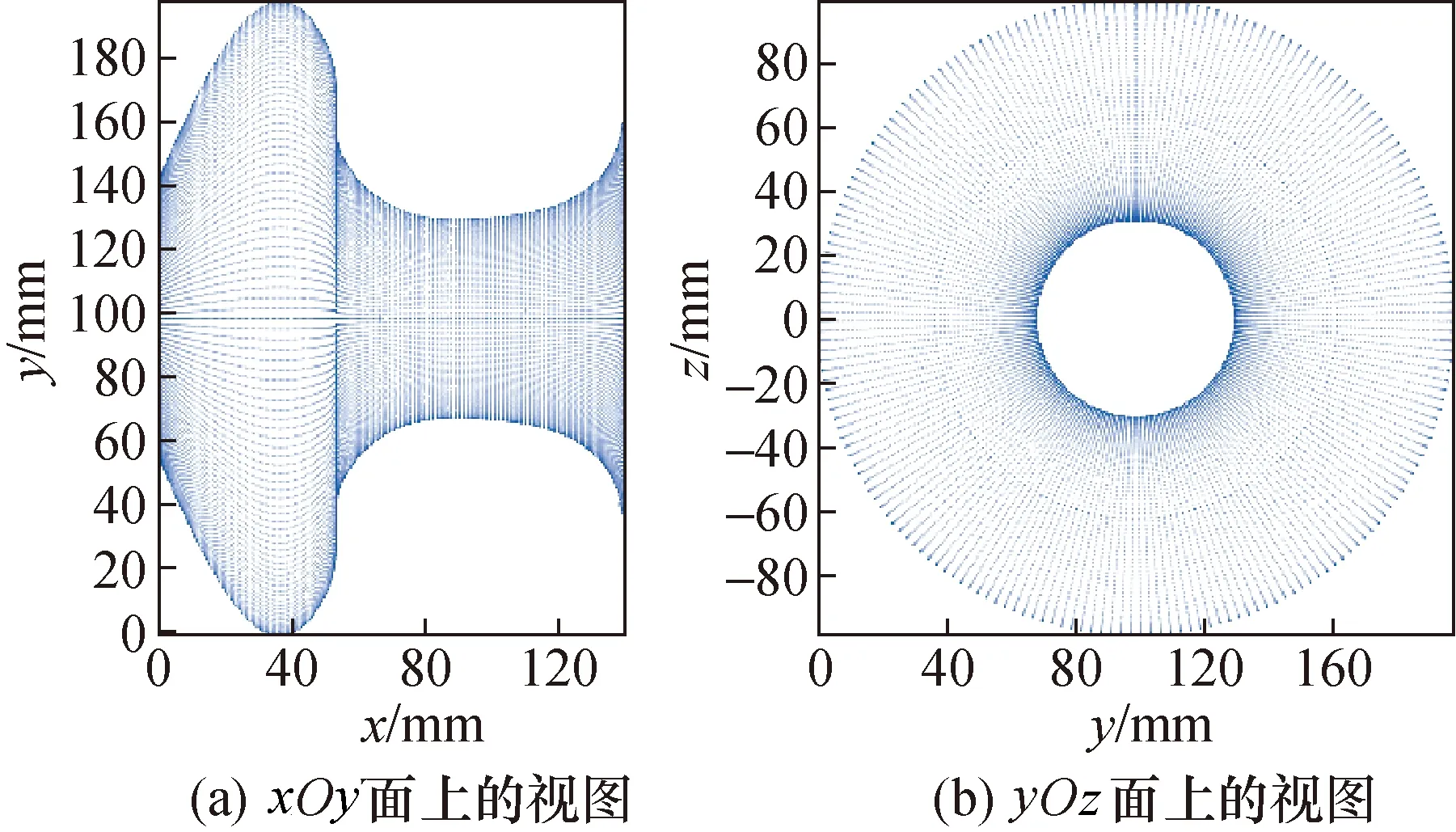
图6 旋转自由曲面的拟合曲面Fig.6 Fitting surface of rotating free-form surface

3.2 拟合曲面形状优化

为了获得更高精度的NURBS拟合曲面，利用第2.2节中的方法对上节中得到的拟合曲面形状进行优化，计算拟合曲面与实际模型曲面的高程值得到两曲面之间的差值序列，对差值序列进行滤波反变换，得到的拟合曲面的误差分布曲线如图7所示。

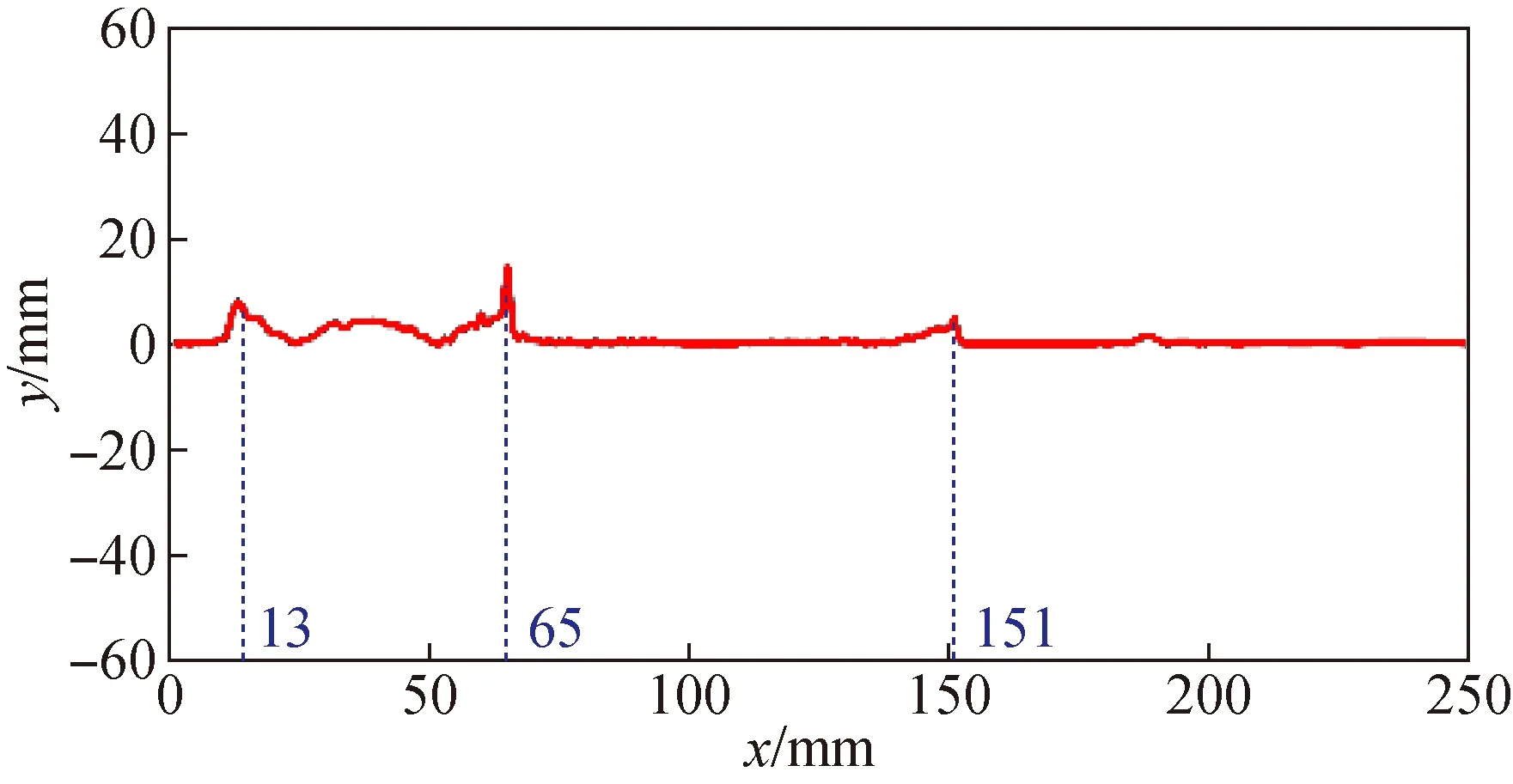
图7 拟合曲面的误差分布Fig.7 Error distribution of fitting surface

表3 数据点与节点 mm

3.3 两种拟合方法对比分析

为了更加直观的了解拟合效果，采用均方根误差对本文方法与文献[4]的传统NURBS拟合方法的拟合结果进行比较。由于本文方法每次曲面形状优化后会加入新的数据点，为保证实验条件一定，使利用传统NURBS方法选取的数据点数量与本文方法每次反插节点后的数据点数量保持一致。利用调整后的拟合曲线对整个旋转自由曲面进行拟合，分析求解获得的拟合曲面与标准曲面之间的误差结果，得到表4中的数据。

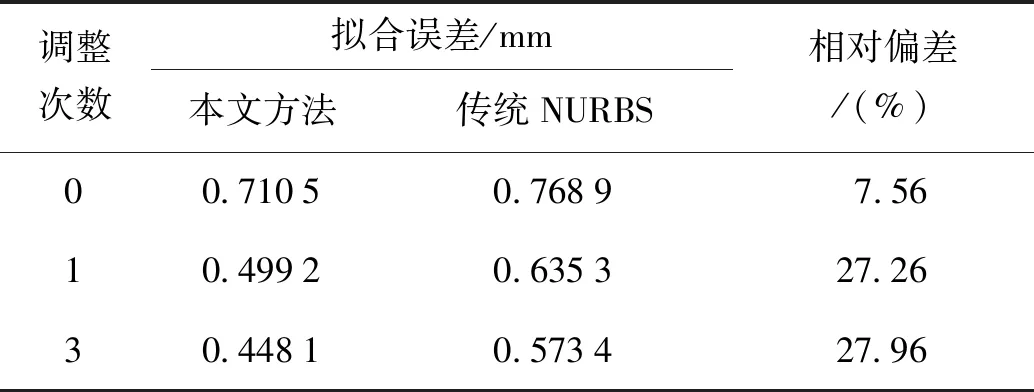
表4 两种方法拟合误差的对比结果Tab.4 Compare results of fitting error of two methods

通过对比表4中两种方法对自由曲面模型在不同调整次数下进行优化的拟合结果可以看出，在相同的调节次数下，本文方法得到的拟合曲面的均方根误差降低了约28%，说明基于分数阶傅里叶变换的NURBS拟合方法能够实现对自由曲面的高精度拟合。且本文方法1次调整后的误差低于传统NURBS拟合方法3次调整后的误差，即对于同一曲面，利用本文方法进行曲面形状优化可以减少调整次数，简化拟合过程。

图8给出了利用两种方法对拟合曲线进行优化后的拟合结果。可以看出图8(b)中调整1次的拟合曲线拟合效果优于图8(a)中初始拟合曲线。本文方法的拟合曲线更贴近于实际点云数据曲线。

图8 两种方法的拟合结果Fig.8 Fitting results of two methods

4 结 论

本文提出了一种基于分数阶傅里叶变换的NURBS曲面拟合方法。利用分数阶傅里叶变换对自由曲面模型的点云数据进行处理，能够快速、高精度地从点云数据中提取出自由曲面模型的表面结构特征。根据提取的特征信息选取合适的拟合参数对自由曲面模型的拟合曲面进行曲面优化，与传统NURBS拟合方法相比，拟合曲面的均方根误差降低了约28%，具有更优的拟合效果，且能减少曲面优化的调整次数，简化NURBS曲面拟合过程。