Generalized Truncated Fr´echet Generated Family Distributions and Their Applications
2021-04-26RamadanZeinEldinChristopheChesneauFarrukhJamalMohammedElgarhyAbdullahAlmarashiandSanaaAlMarzouki
Ramadan A.ZeinEldin,Christophe Chesneau,Farrukh Jamal,Mohammed Elgarhy,Abdullah M.Almarashi and Sanaa Al-Marzouki
1Deanship of Scientific Research,King AbdulAziz University,Jeddah,21589,Saudi Arabia
2Faculty of Graduate Studies for Statistical Research,Cairo University,Al Orman,Giza Governorate,12613,Egypt
3Universit´e de Caen,LMNO,Campus II,Science 3,Caen,14032,France
4Department of Statistics,The Islamia University of Bahawalpur,Punjab,63100,Pakistan
5The Higher Institute of Commercial Sciences,Al Mahalla Al Kubra,Algarbia,31951,Egypt
6Statistics Department,Faculty of Science,King AbdulAziz University,Jeddah,21551,Saudi Arabia
ABSTRACT Understanding a phenomenon from observed data requires contextual and efficient statistical models.Such models are based on probability distributions having sufficiently flexible statistical properties to adapt to a maximum of situations.Modern examples include the distributions of the truncated Fr´echet generated family.In this paper,we go even further by introducing a more general family,based on a truncated version of the generalized Fr´echet distribution.This generalization involves a new shape parameter modulating to the extreme some central and dispersion parameters,as well as the skewness and weight of the tails.We also investigate the main functions of the new family,stress-strength parameter,diverse functional series expansions,incomplete moments,various entropy measures,theoretical and practical parameters estimation,bivariate extensions through the use of copulas,and the estimation of the model parameters.By considering a special member of the family having the Weibull distribution as the parent,we fit two data sets of interest,one about waiting times and the other about precipitation.Solid statistical criteria attest that the proposed model is superior over other extended Weibull models,including the one derived to the former truncated Fr´echet generated family.
KEYWORDS Truncated distribution;general family of distributions;incomplete moments;entropy;copula;data analysis
1 Introduction
Determining the underlying distribution of data is a crucial topic in many applied fields,such as medicine,reliability,finance,economics,engineering and environmental sciences.Among the possible approaches,one can define general families of continuous distributions from wellestablished parental distributions,having enough interesting properties to offer statistical models that adapt to all possible situations.The constructions of such families are based on specific mathematical techniques which may depend on one or several tunable parameters.For an overview on classic families of distributions and the associated techniques,we refer the reader to the surveys of [1-3].
In recent studies,the composition-truncation technique by [4] has been used to develop families of distributions achieving the goals of simplicity and efficiency.Among them,there are the truncated exponential-G family by [5],truncated Fréchet-G family by [6],truncated inverted Kumaraswamy-G family by [7],truncated Weibull-G family by [8],truncated Cauchy power-G family by [9],truncated Burr-G family by [10],type II truncated Fréchet-G family by [11],truncated log-logistic-G family by [12],right truncated T-X family by [13] and truncated Lomax-G family by [14].The functions defining these families have the advantages of being simple,with a reasonable number of parameters,and having original monotonic and non-monotonic forms,which makes them attractive for statistical applications.
Especially,the truncated Fréchet-G family innovates in the following aspects:(i) Its functions are quite manageable,with a corresponding cumulative distribution function (CDF) having a simple exponential expression,(ii) It has a reasonable number of parameters:two plus those of the parental distribution,and (iii) Provides distributions with original monotonic and nonmonotonic shapes,as shown in [6] with the gamma distribution as the parent.The combination of these qualities makes this family unique compared to others,and also attractive for statistical purposes.However,the price of the simplicity is that the nice flexibility of these distributions depends strongly on the choice of the parental distribution.And,to our knowledge,only the special distribution based on the gamma distribution has been explored in detail.
In this paper,we take one more step in this direction,by proposing a generalization of the truncated Fréchet-G family.It is also based on the composition-truncation technique,but uses a generalized version of the truncated Fréchet distribution called generalized Fréchet (GFr)distribution.First,the GFr distribution is defined by the following CDF:

whereα,β,λ>0,(andFGFr(x;α,β,λ)=0 otherwise).This distribution is also known under the names of exponentiated Fréchet distribution and exponentiated Gumbel type-2 distribution pioneered by [15,16].As an alpha property,the GFr distribution is connected with the famous exponentiated exponential (EE) distribution introduced by [17] in the following sense:ifXdenotes a random variable (RV) following the GFr distribution with parametersα,βandλ,thenX−λfollows the EE distribution with parametersαandβ.The GFr distribution contains the former Fréchet distribution,obtained by takingβ=1.Also,it is proved in [15,16] that the parameterβmakes the GFr model really more pliant than the former Fréchet model.This has motivated the study of some of its extensions,as the successful one proposed in [18].Here,we exploit the features of the GFr distribution to define a new general family of distributions.Following the spirit of [4],we first derive the truncated generalized Fréchet distribution over the interval (0,1),specified by the following CDF:

that is

We complete this definition by assuming thatFTGFr(x;α,β,λ)=0 forx≤0 andFTGFr(x;α,β,λ)=1 forx≥1.As far as we know,this truncated distribution is unlisted in the literature,and can be of independent interest.Here,we use it to define the truncated generalized Fréchet generated (TGFr-G) family of (continuous) distributions by considering the CDF obtained as
FTGFr−G(x;ψ)=FTGFr(G(x;η);α,β,1),x∈R,
that is

whereG(x;η)denotes the CDF of a parent (continuous) distribution andψ= (α,β,η).Note that we have putλ=1 in the definition of (2) to avoid the over-parameterization phenomenon;if necessary,one may re-introduce it easily by replacingG(x;η)byG(x;η,λ)=H(x;η)λ,whereH(x;η)is a continuous CDF.One can observe that the TGFr-G and truncated Fréchet-G families coincide by takingβ=1.The main innovation of the TGFr-G family remains in its definition involving the shape parameterβwhich opens new modelling perspectives,in the same spirit as the GFr distribution extends those of the classic Fréchet distribution.In this study,we formalize this claim by pointing out the desirable mathematical properties and applicability of the TGFr-G family.In particular,we investigate the precise role ofβin the features of the main functions,stress-strength parameter,incomplete moments and various entropy measures.The parameters estimation and bivariate extensions are also discussed,as well as a complete estimation work on the parameters.The applicable aspect of the new family is mainly highlighted by a special three-parameter distribution,defined with the Weibull distribution as the parent.It is called the truncated generalized Fréchet Weibull (TGFrW) distribution.For the related model,the maximum likelihood estimates of the parameters are derived and a simulation study is also made to check their accuracy.Then,two data sets are considered to evaluate how good the fit of the proposed model is.Diverse criteria are used in this regard,pointing out that the fit of the TGFrW model is better to those of comparable Weibull type models,with possible more parameters.In particular,the proposed model surpasses the analogous truncated Fréchet model,attesting to the importance of the findings.
The following organization is adopted.The TGFr-G family is defined in Section 2.Diverse properties are discussed in Section 3,including the analytical study of the main functions,stress-strength parameter,series expansions,incomplete moments with derivations,various entropy measures,theoretical and practical parameters estimation and various bivariate extensions of the proposed family through the use of copulas.Section 4 is devoted to the TGFrW distribution,with an emphasis on its applicability in simulated and concrete statistical settings.Section 5 contains some concluding notes.
2 The TGFr-G Family
The basics of the TGFr-G family are proposed in this section,exhibiting its main functions of interest,as well as a short list of special distributions.
2.1 First Approach
First of all,we recall that the CDF given as (3) defines the TGFr-G family.Hereafter,a RVXhaving the CDF given as (3) is denoted byX~TGFr-G(ψ).By takingβ=1,it corresponds to the special case of the truncated Fréchet-G family by [6].
Among the important functions of the TGFr-G family,there are the PDF given as

and the hazard rate function (HRF) obtained as


Table 1:Some special distributions belonging to the TGFr-G family
The analytical properties of these functions are very informative on the data fitting possibilities of the associated models.This aspect will be the subject of further discussions.Also,the quantile function (QF),obtained by inverting the CDF in (3),is given as

whereQ(u;η)denotes the QF of the parental distribution.The fact thatQTGFr−G(u;ψ)has a closed-form expression is a plus for the TGFr-G family.In particular,we can simply determine the median asM=QTGFr−G(1/2;ψ),derive several functions related to this QF and generate random values through the inverse transform sampling method.
In order to illustrate the heterogeneity of the TGFr-G family,Tab.1 lists several of its members based on standard parental distributions,with various supports and numbers of parameters.
In our applications,a focus will be put on the TGFrW distribution defined withθ=1.This choice is motivated by upstream numerical and graphical investigations.
3 General Properties
In this section,we develop some notable properties of the TGFr-G family,and discuss some new motivations.
3.1 Equivalences
Here,some analytical results on the functions of the TGFr-G family are studied.Firstly,we investigate the equivalences ofFTGFr−G(x;ψ),fTGFr−G(x;ψ)andhTGFr−G(x;ψ).Mathematical facts force us to distinguish the cases:G(x;η)→0,G(x;η)→1,α→0,α→+∞,β→0 andβ→+∞.It is assumed thatG(x;η)∈(0,1) for these four last cases,butG(x;η)→0 andG(x;η)→1 are not excluded.
Let us mention thatG(x;η)→0 is equivalent to say thatxtends to the lower limit of the adherence of the set {x∈R;G(x;η)>0},andG(x;η)→1 is equivalent to say thatxtends to the upper limit of the adherence of the set {x∈R;G(x;η)<1}.The obtained equivalences forFTGFr−G(x;ψ)andfTGFr−G(x;ψ)are described in Tab.2.
From Tab.2,the following remarks hold.WhenG(x;η)→0,we see thatαhas a significant impact on the limit offTGFr−G(x;ψ).In particular,the terme−αG(x;η)−1can dominateg(x;η)/G(x;η)2and thusfTGFr−G(x;ψ)→0 with an exponential decay.WhenG(x;η)→1,for the limit offTGFr−G(x;ψ),bothαandβinfluence the proportionality constant,but the limit comportment ofg(x;η)remains determinant.Whenα→0 orα→+∞withG(x;η)<1 and fixg(x;η),we havefTGFr−G(x;ψ)→0.Whenβ→0,the limiting function ofFTGFr−G(x;ψ)is obtained as

and one can remark thatF∗(x;α,η)is a valid CDF.As far as we know,it is unlisted in the literature,offering a new and original “logarithmic-exponential-G family”.This finding also reveals the richness of the proposed TGFr-G family.
Tab.3 completes Tab.2 by investigating the equivalences ofhTGFr−G(x;ψ).

Table 2:Equivalences for the CDF and PDF of the TGFr-G family

Table 3:Equivalences for the HRF of the TGFr-G family
From Tab.3,whenG(x;η)→0,we see that the limit ofhTGFr−G(x;ψ)truly depends onα,which is not the case whenG(x;η)→1,where the limiting function correspond to the HRF of the parental distribution.In the case whereG(x;η)→1 is excluded andα→0,we have
showing the importance of the parameterβin this regard.Note that,when bothG(x;η)→1 andα→0,with a fixg(x;η),we havehTGFr−G(x;ψ)~(β/αβ)g(x;η)→+∞.Also,whenG(x;η)→1 is excluded,with fixg(x;η)andG(x;η),andα→+∞,we havehTGFr−G(x;ψ)→0.The obtained limit whenβ→0 is a complex function with respect tox,and,whenG(x;η)→1 is excluded,with fixg(x;η)andG(x;η),andβ→+∞,we have

implying thathTGFr−G(x;ψ)→+∞.
3.2 Mode(s)Analysis
A mode of the TGFr-G family belongs to the set argmaxx∈RfTGFr−G(x;ψ).Such a mode,sayxm,
• is a solution of the following equation:

whereg(x;η)′denotes the derivative ofg(x;η)with respect tox,
• satisfies the following inequality:

whereg(x;η)′′denotes the two times derivative ofg(x;η)with respect tox.
The number and definition(s) of the mode(s) depend on the parental distribution,αandβ.However,even though all of these quantities are known,the complexity of the above equations constitutes an obstacle to get an analytical expression of the mode(s).Thus,mathematical software seems necessary for any numerical appreciation.
3.3 Stress-Strength Parameter
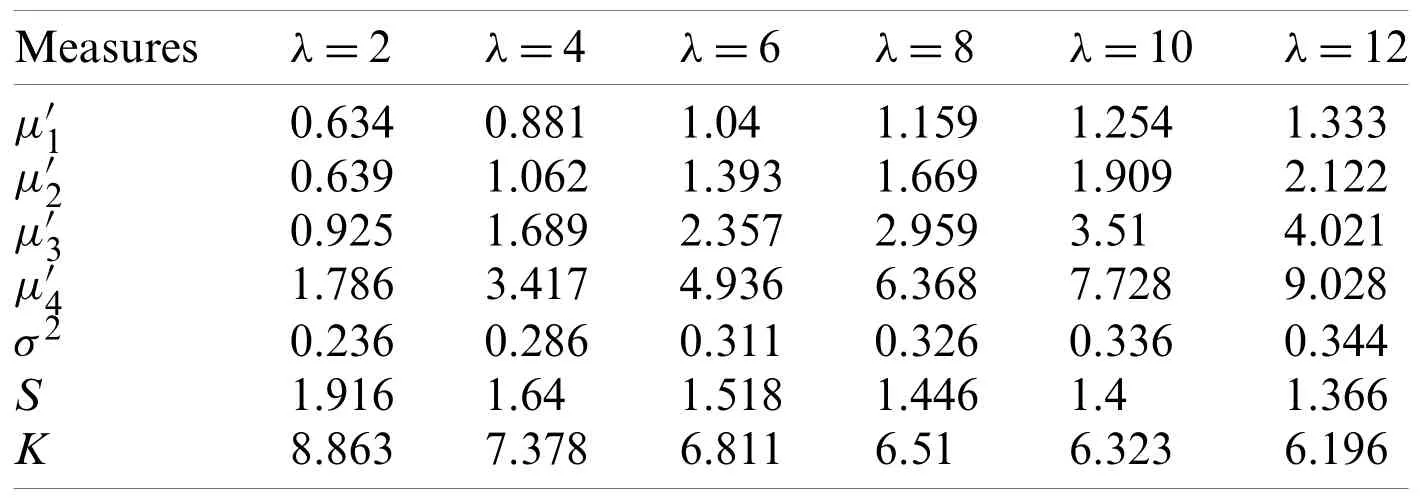
The stress-strength parameter provides one of the most important measurements in reliability analysis.From two independent RVsXandY,the stress-strength parameter is defined byR=P(Y The following result shows that,under a certain scenario on the parameters,a stress-strength parameter associated to the TGFr-G family has a tractable analytical expression. Proposition 3.1.Letψ1=(α,β1,η),ψ2=(α,β2,η),X1~TGFr-G(ψ1),X2~TGFr-G(ψ2),withX1andX2independent,andR=P(X2 Proof.The independence ofX1andX2,and (3),imply that Now,by virtue of (4) and some developments,we get whereψ∗= (α,β1+β2,η).By putting the above equations together and usingwe obtain This ends the proof of Proposition 3.1. From Proposition 3.1,we can note thatRis finally independent of the chosen parental distribution.Also,whenβ1=β2,X1andX2are identically distributed andRtakes the value 1/2 as expected in this simple case.The manageable expression ofRis useful for estimation purposes;with the plug-in approach,α,β1andβ2can be substituted by adequate estimates to derive an estimate forR.Further developments in this regard are however out the scope of this study. The following proposition proves that the “possibly complex”exponentiated PDFfTGFr−G(x;ψ)τcan be simply expressed as a series depending on parental exponentiated functions.Such expansion is useful for diverse algebraic manipulations offTGFr−G(x;ψ)τinvolving differentiation or integration,as discussed in full generality in [21]. Proposition 3.2.Letτ>0.The two following complementary expansions hold forfTGFr−G(x;ψ)τ: A1:In terms ofg(x;η)τand exponentiated survival functions of the parental distribution,i.e.,(x;η)=1−G(x;η),we have A2:In terms ofg(x;η)τand exponentiatedG(x;η),we have Proof.Owing to (4),we get Now,the exponential expansion gives At this stage,two complementary decompositions forG(x;η)−ℓ−2τcan be studied separately. To obtain A1:One can expressG(x;η)−ℓ−2τin terms of exponentiated ¯G(x;η)via the generalized binomial theorem as To obtain A2:One can expressG(x;η)−ℓ−2τin terms of exponentiatedG(x;η)via the generalized and standard binomial theorems as The proof of Proposition 3.2 ends by putting all the above expansions together. Several applications of Proposition 3.2 will be presented later. The incomplete moments ofX~TGFr-G are useful to derive crucial measures and functions of the TGFr-G family,with a high potential of applicability.Mathematically,therthincomplete moment ofX~TGFr-G at anyt∈R can be expressed as that is,thanks to (4), For some special parental distributions,the calculus of this integral by usual integration techniques is not excluded.However,for further analytical manipulations or evaluation,a series expression is sometimes preferable.In this regard,several possibilities are presented below,depending on the level of complexity in the definition ofG(x;η). B1:From (6),by applying the change of variableand the generalized binomial expansion,assuming that the integral and sum signs are interchangeable,we get where If the QF of the parental distribution is not too complex,the integral term can be made explicit. B2:For more universal series developments,Proposition 3.2 applied withτ=1 gives series expansions offTGFr−G(x;ψ)that can be injected into (6).For instance,by considering the expression A1,assuming that the integral and sum signs are interchangeable,we get Alternatively,under the same conditions,the application of A2 gives For a wide panel of parental distributions,the integralsandare available in the literature or easily calculable.Also,for practical aims,one can truncate the infinite sums by any large integer to have suitable approximation functions forμ′r(t).Further detail on the interest of such series expansions in the treatment of various probabilistic measures can be found in [21]. As example of applications,from the incomplete moments ofX~TGFr-G,we can derive therthraw moments ofXdefined byμ′r=E(Xr)=limt→+∞μ′r(t),therthcentral moment ofXspecified by the following relation:the variance ofXgiven asσ2=V(X)=μ2,the general coefficient ofXdefined byCr=μr/σrallowing to define the skewness coefficient corresponding toS=C3and the kurtosis coefficient obtained asK=C4,among others. Also,from the mean incomplete momentμ′1(t),that isμ′r(t)taken withr=1,one can express the mean deviation ofXaboutμ′1asδ1=E(|X−μ′1|)=2μ′1FTGFr−G(μ′1;ψ)−2μ′1(μ′1),the mean deviation aboutMasδ2=E(|X−M|)=μ′1−2μ′1(M),the mean residual life asm(t)=E(X−t|X>t)=[1−μ′1(t)]/[1−FTGFr−G(t;ψ)]−t,the mean waiting time asM(t)=E(t−X|X≤t)=t−μ′1(t)/FTGFr−G(t;ψ),the Bonferroni curve asB(u)=μ′1(QTGFr−G(u;ψ))/(uμ′1),u∈(0,1),and the Lorenz curve asL(u)=uB(u),u∈(0,1). The entropy is a fundamental concept in information theory,with applications in statistical inference,neurobiology,linguistics,cryptography,quantum computer science and bioinformatics.In the literature,there exists several entropy measures to determine the randomness of a distribution.Most of them are discussed in the survey of [22].By considering a generic (continuous)distribution with PDF denoted byf(x),some of them are presented in Tab.4.In this table,it is supposed thatθ>0 andθ/=1. From Tab.4,we see that the main term in the definitions of the entropy measures is the following integral term:f(x)θdx.We now investigate it in the context of the TGFr-G family.So,we set Table 4:Some entropy measures of a distribution with PDF denoted by f(x) withθ>0 andθ/=1.Thanks to (4),it can be expressed as For some special parental distributions,we can inspect the calculus of this integral by standard techniques.A more universal approach consists in expressing it as a tractable series expansion.Hence,once can apply Proposition 3.2 with the choiceτ=θto obtain series expansions offTGFr−G(x;ψ)θand use it into (8).Thus,assuming that the integral and sum signs are interchangeable,from A1,we get Alternatively,under the same conditions,the application of A2 gives For most of the standard parental distributions,the integralsandcan be determined with mathematical efforts.Thus,one can deduce expansions of all the entropy measures presented in Tab.4.In particular,the Tsallis entropy of the TGFr-G family can be expanded as One can deduce a precise approximation of it by truncating the infinite sum by any large integer. The main objective of the TGFr-G family is to provide pliant semi-parametric models for statistical applications.To reach this aim,the estimation of the model parameters is a crucial step,and several methods of estimation are possible.Here,we provide the essential theory on the maximum likelihood (ML) method of estimation in the context of the TGFr-G family.The generalities can be found in [28]. First of all,letX1,...,Xnbenindependent and identically distributed RVs fromX~TGFr-G(ψ)and X=(X1,...,Xn).Then,assuming that they are unique,the ML estimators of the parametersα,βandη,say,and,respectively,are the RVs obtained as Assuming thatL(ψ,X) is differentiable with respect toψ,the ML estimators are the solutions of the following equations:∂ℓ(ψ,X)/∂α=0,∂ℓ(ψ,X)/∂β=0 and∂ℓ(ψ,X)/∂η=0,whereℓ(ψ,X)=ln[L(ψ,X)].In most of the cases,there are no analytical expressions for these estimators,but practical solutions exist and will be discussed later.Then,under some regularity conditions,the ML estimators satisfy remarkable convergence properties,including the asymptotically normal property presented below.Letmbe the number of components inψ(which can be numerous sinceηis itself a vector of components) andψube theuthcomponent ofψ.Then,the asymptotic distribution ofis the multivariate normal distributionNm(ψ,J(ψ)−1),whereJ(ψ)denotes them×mcovariance matrix defined by In a concrete statistical scenario,we deal with data corresponding to observations ofX1,...,Xn.Let us denoted them byx1,...,xn.Then,the ML vector of estimates ofψ,sayis defined by the corresponding observation of ˆψ.Thanks to the argmax definition,it can be obtained numerically by optimization via the use of any Newton-Raphson type algorithm.With the R software,this numerical work can be done via the functions of the package AdequacyModel. For the practice of the asymptotic normality,the covariance matrixJ(ψ)is often difficult to determine analytically and depends on the unknown parameters.A standard approach consists in using the following approximation:where x=(x1,...,xn).Thus,the asymptotic distribution ofcan be considered as the multivariate normal distributionNm(ψ,I−1),whereThis result is useful to construct asymptotic two-sided confidence intervals (CIs) of the parameters.More precisely,for anyu=1,...,mandν∈(0,1),the 100(1−ν)% CI ofψuis obtained as CI=[LB,UB], where LB and UB are the lower and upper bounds of the interval,defined by LB=LBψu(ν)=andrespectively,whereduis theuthcomponent in the diagonal ofI−1andz1−ν/2is the quantile of the normal distributionN(0,1) taken at 1−ν/2.As the main interpretation,there is 100(1−ν)% of chances thatψubelongs to CI,which is of interest by takingνsmall enough.The typical values forνare 0.01,0.05 or 0.1.Finally,by the invariance property of the ML estimates,we can deduce ML estimates of several measures of the TGFr-G family.For instance,we can inspect the estimation of the Tsallis entropy of the TGFr-G family as defined in (9);the ML estimate ofTθ(ψ)is naturally obtained as The ML estimates,CIs and estimate of the Tsallis entropy will be the object of a numerical study later,by the consideration of a special distribution of the TGFr-G family. Bivariate families of distributions are of interest to model distributions behind two dimensional phenomena or measures,observed via bivariate data.This remains an actual demand in regression or clustering analysis,among others.The univariate TGFr-G family can be extended to the bivariate case via several approaches.The most natural one is to use a bivariate parental distribution characterized by a bivariate CDF,sayG(x,y;η),whereηis the vector of parameters.Thus,based on (3),we can define the 2TGFr-G family by the following bivariate CDF: whereψ= (α,β,η).Then,it is clear that,if (X,Y)~2TGFr-G,thenX~TGFr-G andY~TGFr-G.However,the structure of dependence betweenXandYremains unmanageable.A more technical approach but with a clear dependence structure consists in employing special functions called copulas. • By using the Farlie-Gumbel-Morgenstern copula,a bivariate extension of the TGFr-G family,called FGMTGFr-G family,is defined by the bivariate CDF given as whereλ∈[−1,1],(x;ψ1) and(y;ψ2) are defnied as (3) with possibly different parental CDFs,sayG1(x;ψ1) andG2(y;ψ2),respectively.Note that the independence copula corresponds to the caseλ=0. • By using the Clayton copula,a bivariate extension of the TGFr-G family,called CTGFr-G family,is defined by the bivariate CDF specified by whereλ≥−1 andλ/=0,by keeping the previous notations. Other interesting bivariate extensions can be derived from other notorious copulas.A complete list of them,with more theoretical elements,can be found in [29]. The TGFr-G family contains a plethora of potential interesting distributions.Here,we emphasize with the truncated generalized Fréchet Weibull (TGFrW) distribution as presented in Tab.1,discussing its numerous qualities. Let us recall that the TGFrW distribution as described in Tab.1 withθ=1 corresponds the following configuration:η=λ,G(x;λ)=1−e−xλ,x>0,(G(x;λ)=0 otherwise),andg(x;λ)=λxλ−1e−xλ,x>0.Concretely,it is defined by the following CDF: (andFTGFrW(x;α,β,λ)=0 otherwise).The corresponding PDF is given as The HRF is obtained as The pliancy of the curvatures offTGFrW(x;α,β,λ)andhTGFrW(x;α,β,λ)is illustrated in Figs.1 and 2,respectively. In Fig.1,various degrees of skewness (asymmetry) and kurtosis are observed forfTGFrW(x;α,β,λ),showing decreasing and bell shapes,as well various weights on the right tail mainly.In Fig.2,we see thathTGFrW(x;α,β,λ)possesses reversed J,bathtub decreasing and increasing shapes,with possibly several critical points. Thanks to (5),the QF can be expressed as Figure 1:Some curves of the PDF of the TGFrW distribution Figure 2:Some curves of the HRF of the TGFrW distribution Hence,quartiles and random generations numbers from the TGFrW distribution can be easily investigated. The general properties studied for the TGFr-G family in Section 2 can be applied to the TGFrW distribution.A selection of them are presented below.First of all,in order to complete the observations made on Figs.1 and 2,let us investigate the equivalences and limits offTGFrW(x;α,β,λ)andhTGFrW(x;α,β,λ).Whenx→0,we have Also,whenx→+∞,we have In particular,we note thatλplays the major role in these convergence,limx→0fTGFrW(x;α,β,λ)=limx→+∞fTGFrW(x;α,β,λ)=0 in all cases,and,whenx→+∞,hTGFrW(x;α,β,λ)has the same comportment to the HRF of the parental distribution,i.e.,hTGFrW(x;α,β,λ)→0 whenλ<1,hTGFrW(x;α,β,λ)→1 whenλ=1,andhTGFrW(x;α,β,λ)→+∞whenλ>1. Also,by the Riemann integral criteria,the equivalence results forfTGFrW(x;α,β,λ)ensure that the raw moments of all orders ofX~TGFrW exist,for all the values of the parameters.In this setting,let us now discuss therthincomplete moment ofX,rthraw moment ofXwith related measures,and the Tsallis entropy. As usual,therthincomplete moment ofXcan be expressed as its principal integral form.Alternatively,owing to (7) and the equality:whereγ(a,x)=denotes the lower incomplete gamma function,we have We can manipulate this expansion to derive approximations of the measures and functions presented in Subsection 3.5.Also,by applyingt→+∞,we get therthraw moment ofX,i.e., whereΓ(a)=As numerical works,Tabs.5 and 6 collected the numerical values of some measures of the TGFrW distribution derived to the raw moments. Among others,Tabs.5 and 6 show how the values of some moments measures ofX~TGFrW can vary according to the values of the parameters.Here,a great variation of the values on the mean and kurtosis are mainly observed. As described in Subsection 3.6,the Tsallis entropy of the TGFrW distribution is initially defined by an integral expression.A tractable series expansion can be deduced from (9).Indeed,since=λθ−1(m+θ)−(θ−1)(λ−1)/λ−1Γ((θ−1)(λ−1)/λ+1) provided thatλ>max(1−1/θ,0),we have Possible values for the Tsallis entropy are shown in Tab.7. Table 5:Values of some measures of the TGFrW distribution for several values of λ and at α=β=0.5 Table 6:Values of some measures of the TGFrW distribution for several values of λ and at α=0.7 and β=3.0 Table 7:Values of the Tsallis-entropy of the TGFrW distribution for several values of the parameters Tab.7 reveals that the amount of randomness of the TGFrW distribution measured by the Tsallis entropy is versatile.Indeed,it can take negative values,as well as small or large positive values.The rest of the study focuses on the statistical usefulness of the TGFrW model in a statistical framework. The ML estimates of the parameters of the TGFrW model,the corresponding CIs and the estimate of the Tsallis entropy can be obtained via the approach described in Subsection 3.7.Here,we provide a numerical study on these statistical objects through the simple random sampling scheme.This scheme is based on the QF defined by (10).A performance study of the estimates is conducted relatively to the mean square errors (MSEs),(average) LBs and UBs of the corresponding 90% and 95% CIs,as well as the corresponding average lengths (ALs),i.e.,AL=UB−LB.The software Mathematica 9 is used in this regard.The following steps are followed. Step 1:A random sample of values of sizen=100,200,300,1000 and 3000 is generated from the TGFrW distribution. Step 2:We consider the following sets of parameters:set1:(α=0.5,β=2.0,λ=0.5),set2:(α=0.5,β=2.0,λ=0.3),set3:(α=0.3,β=1.6,λ=0.3) and set4:(α=0.5,β=0.8,λ=0.3). Step 3:For each of the above sets and each sample of sizen,the ML estimates are computed. Step 4:We repeat the previous stepsNtimes,dealing with different samples,whereN=5000.Then,the MSEs of the estimates are computed. Step 5:Also,the LBs,UBs and ALs of the 90% and 95% CIs are calculated. Step 6:Numerical outcomes are given in Tabs.8-11. Table 8:Values of ML estimates and IC measures related to the TGFrW model for set1:(α=0.5,β=2.0,λ=0.5) Table 9:Values of ML estimates and IC measures related to the TGFrW model for set2:(α=0.5,β=2.0,λ=0.3) Table 10:Values of ML estimates and IC measures related to the TGFrW model for set3:(α=0.3,β=1.6,λ=0.3) Table 11:Values of ML estimates and IC measures related to the TGFrW model for set4:(α=0.5,β=0.8,λ=0.3) For all the considered sets of parameters,the values in Tabs.8-11,indicate that the ML estimates stabilize to the right values asnincreases.Also,the MSEs and ALs decrease and tend to 0 asnbecomes large as expected. Now,we check the numerical performance of the estimate of the Tsallis entropy of the TGFrW model as described in Subsection 3.7.In this regard,Tabs.12-15 list the values of this estimate under the simulation scenario described above.We adopt the criteria of the relative bias(RB),defined as RB=(Estimate−Exact value)/Exact value. Table 12:Values of the Tsallis entropy estimates related to the TGFrW model for set 1:(α=0.5,β=2.0,λ=0.5) Table 13:Values of the Tsallis entropy estimates related to the TGFrW model for set 2:(α=0.5,β=2.0,λ=0.3) Table 14:Values of the Tsallis entropy estimates related to the TGFrW model for set 3:(α=0.3,β=1.6,λ=0.3) Table 15:Values of the Tsallis entropy estimates related to the TGFrW model for set 4:(α=0.5,β=0.8,λ=0.3) For all the considered sets of parameters,the values in Tabs.8-11,indicate that the estimates of the Tsallis entropy stabilize to the exact values asnincreases.Also,the RBs decrease and tend to 0 asnbecomes large,which is a consistent observation with the expected theoretical convergence. Here,we show that the TGFrW model is ideal to fit practical data of various kinds,with better results in comparison to solid extended Weibull models.More specifically,the two following data sets are considered. The first data set,called datasetI,contains 100 observations on minutes waiting time before a client receives the desired service in a bank.It is:datasetI={0.8,0.8,1.3,1.5,1.8,1.9,1.9,2.1,2.6,2.7,2.9,3.1,3.2,3.3,3.5,3.6,4,4.1,4.2,4.2,4.3,4.3,4.4,4.4,4.6,4.7,4.7,4.8,4.9,4.9,5.0,5.3,5.5,5.7,5.7,6.1,6.2,6.2,6.2,6.3,6.7,6.9,7.1,7.1,7.1,7.1,7.4,7.6,7.7,8,8.2,8.6,8.6,8.6,8.8,8.8,8.9,8.9,9.5,9.6,9.7,9.8,10.7,10.9,11.0,11.0,11.1,11.2,11.2,11.5,11.9,12.4,12.5,2.9,13.0,13.1,13.3,13.6,13.7,13.9,14.1,15.4,15.4,17.3,17.3,18.1,18.2,18.4,18.9,19.0,19.9,20.6,21.3,21.4,21.9,23,27,31.6,33.1,38.5}.The reference for this data is [30]. The second data set,called datasetII,represents 30 successive values of precipitation (in inches),in one month,in Minneapolis.It is:datasetII={0.77,1.74,0.81,1.20,1.95,1.20,0.47,1.43,3.37,2.20,3.00,3.09,1.51,2.10,0.52,1.62,1.31,0.32,0.59,0.81,2.81,1.87,1.18,1.35,4.75,2.48,0.96,1.89,0.90,2.05}.The reference for this data is [31]. The following competitors are taken into account:truncated Fréchet-Weibull (TFrW) model proposed by [6],odd log-logistic Weibull (OLLW) model introduced by [32],beta Weibull (BW)model by [33],exponentiated Weibull (EW) model introduced by [34],and gamma-exponentiated exponential (GE) model studied by [35]. For all the models,the estimation of the parameters are performed via the ML method.We refer to Subsection 3.7 concerning the ML estimates of the TGFrW model.As standard criteria of comparison,the following measures are taken into account:−ˆℓ,AIC,BIC,W,A,KS and p-value (KS),corresponding to the minus estimated log-likelihood function at the data,Akaike information criterion,Bayesian information criterion,Anderson-Darling statistic,Cramervon Mises statistic,Kolmogorov-Smirnov statistic and the p-value of the Kolmogorov-Smirnov test,respectively.The corresponding mathematical formulas are described below. wherenis the number of observations,pis the number of parameters of the considered model,x(1),...,x(n)are the ordered observations,yi=(x(i)),where(x)denotes the estimated CDF of the model involving the ML estimates for the parameters andFn(x)denotes the random empirical CDF.The details on these statistical measures can be found in [36,37]. It is admitted that the smaller the values of AIC,BIC,W,A and KS and the greater the values of p-value (KS),the better the model is to fit to the considered data.The software R is used for all the calculations. For the considered models,the ML estimates with their related standard errors (SEs) are reported in Tabs.16 and 17 for datasetI and datasetII,respectively. Table 16:Values of the ML estimates and SEs for datasetI Table 17:Values of the ML estimates and SEs for datasetII In particular,for datasetI,the parametersα,βandλof the TGFrW model are estimated by=9.6321,=618.6199 and=0.4942,respectively,and for datasetII,they are estimated by=4.7180,=622.2116 and=0.5200,respectively.We remark that the novel parameterβis estimated far from 1,making a strong difference between the estimated TGFrW model and the former estimated TFrW model. Table 18:Values of the considered criteria for datasetI Table 19:Values of the considered criteria for datasetII Figure 3:Various fits of the TGFrW model for datasetI:(a) Estimated PDF,(b) estimated CDF,(c) P-P plot and (d) Q-Q plot From Tabs.18 and 19,it is clear that the TGFrW model is the best of all,with respect to the considered criteria.In particular,it has p-values (KS) closed to 1.As an important remark,the TGFrW model surpasses the former TFrW model,justifying the importance of the generalization. Several kinds of fits of the TGFrW model are shown in Figs.3 and 4 for datasetI and datasetII,respectively.Specifically,the estimated PDFs of the TGFrW distribution are plotted over the corresponding histograms and the estimated CDFs are plotted over the empirical CDFs.The empirical probabilities versus estimated probabilities (P-P) plots and the empirical quantiles versus estimated quantiles (Q-Q) plots are also shown.In all the cases,a near perfect fit is observed,validating the remarkable performance of the TGFrW model. Figure 4:Various fits of the TGFrW model for datasetII:(a) estimated PDF,(b) estimated CDF,(c) P-P plot and (d) Q-Q plot We have motivated the use of the truncated generalized Fréchet distribution to define a new generalized family of continuous distributions,called the truncated generalized Fréchet generated(TGFr-G) family.Diverse mathematical and practical investigations show the full potential of the new family,supported by detailed graphical and numerical evidences.A focus is put on the truncated generalized Fréchet Weibull (TGFrW) distribution,with a complete statistical treatment of the related model.Comparative fitting are performed through the use of two practical data sets,with favorable results to the new model in comparison to other popular extended Weibull models.In particular,under a comparable setting,the new model surpasses the former truncated Fréchet model.As perspectives of future work,other special models of the TGFr-G family may be the subjects of further investigation,specially those with support on R.Also,the bivariate extensions of the TGFr-G family can be explored more,with applications in the fields of regression and clustering,for instance.Also,applications in physics remain an interesting challenge,exploring the possible randomness of various networks [38] and various differential equations [39]. Acknowledgement:We thank the reviewers for their thorough comments and remarks which contributed to improve the quality of the paper.This work was funded by the Deanship of Scientific Research (DSR),King AbdulAziz University,Jeddah,under Grant No.(G:531-305-1441).The authors gratefully acknowledge the DSR technical and financial support.The authors,therefore,acknowledge with thanks to DSR technical and financial support. Funding Statement:This work was funded by the Deanship of Scientific Research (DSR),King AbdulAziz University,Jeddah,under Grant No.G:531-305-1441.The authors gratefully acknowledge the DSR technical and financial support. Conflicts of Interest:Authors must declare all conflict of interests.
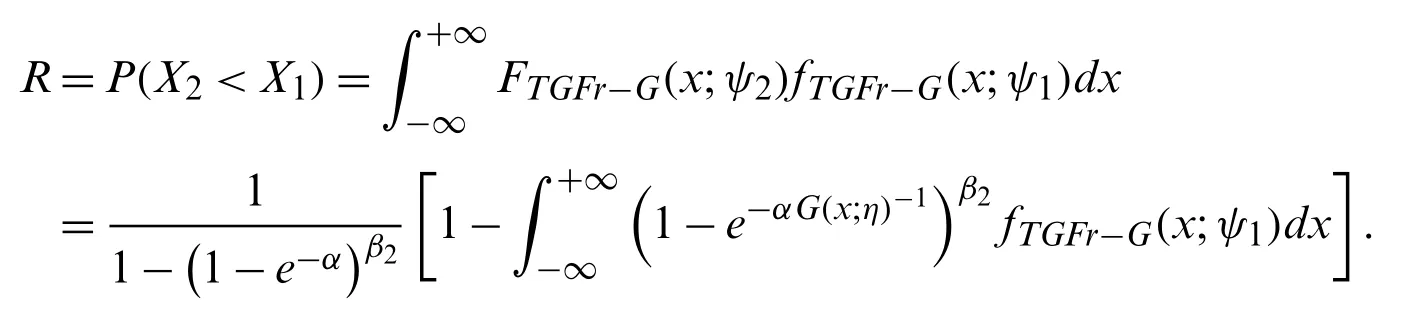


3.4 Representation






3.5 Incomplete Moments with Discussion




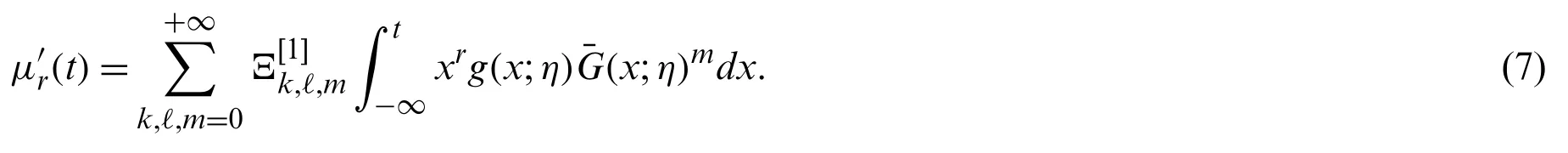

3.6 Entropy





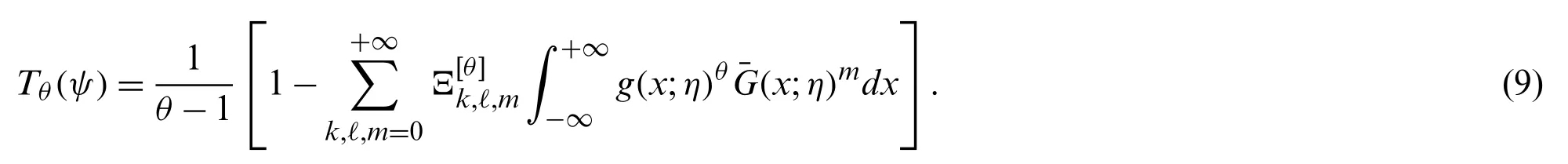
3.7 Parameters Estimation:Theory and Practice


3.8 Bivariate TGFr-G Family


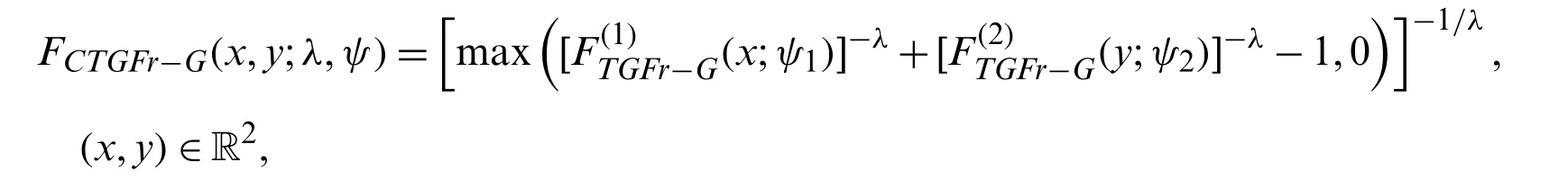
4 The TGFrW Distribution:Theory and Applications
4.1 The TGFrW Distribution

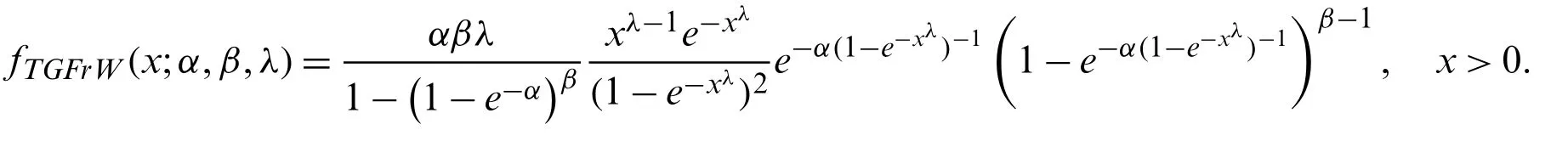




4.2 Some Properties and Numerical Works
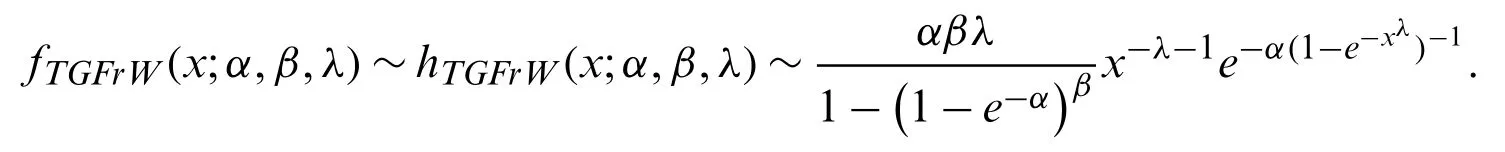






4.3 Estimation:Numerical Study








4.4 Data Analysis
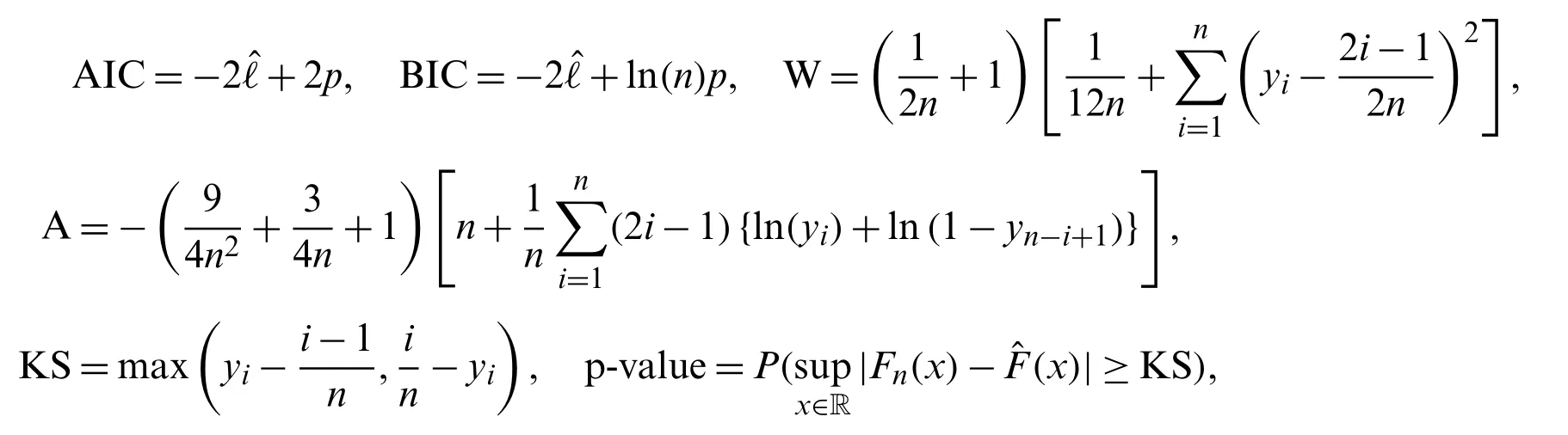






5 Conclusion
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- E-Commerce Supply Chain Process Optimization Based on Whole-Process Sharing of Internet of Things Identification Technology
- Development of TD-BEM Formulation for Dynamic Analysis for Twin-Parallel Circular Tunnels in an Elastic Semi-Infinite Medium
- Shear Induced Seepage and Heat Transfer Evolution in a Single-Fractured Hot-Dry-Rock
- Impacts of Disk Rock Sample Geometric Dimensions on Shear Fracture Behavior in a Punch Shear Test
- An Uncertainty Analysis Method for Artillery Dynamics with Hybrid Stochastic and Interval Parameters
- Stability and Bifurcation of a Prey-Predator System with Additional Food and Two Discrete Delays
