An Improved Higher-Order Time Integration Algorithm for Structural Dynamics
2021-04-26YiJiandYufengXing
Yi Ji and Yufeng Xing
1Institute of Solid Mechanics,Beihang University,Beijing,100083,China
2Shen Yuan Honors College,Beihang University,Beijing,100083,China
ABSTRACT Based on the weighted residual method,a single-step time integration algorithm with higher-order accuracy and unconditional stability has been proposed,which is superior to the second-order accurate algorithms in tracking long-term dynamics.For improving such a higher-order accurate algorithm,this paper proposes a two sub-step higher-order algorithm with unconditional stability and controllable dissipation.In the proposed algorithm,a time step interval[tk,tk+h]where h stands for the size of a time step is divided into two sub-steps[tk,tk+γ h]and[tk+γ h,tk+h].A non-dissipative fourth-order algorithm is used in the first sub-step to ensure low-frequency accuracy and a dissipative third-order algorithm is employed in the second sub-step to filter out the contribution of high-frequency modes.Besides,two approaches are used to design the algorithm parameter γ.The first approach determines γ by maximizing low-frequency accuracy and the other determines γ for quickly damping out highfrequency modes.The present algorithm uses ρ∞to exactly control the degree of numerical dissipation,and it is third-order accurate when 0≤ρ∞<1 and fourth-order accurate when ρ∞=1.Furthermore,the proposed algorithm is self-starting and easy to implement.Some illustrative linear and nonlinear examples are solved to check the performances of the proposed two sub-step higher-order algorithm.
KEYWORDS Time integration algorithm;two-sub-step;higher-order accuracy;controllable dissipation;unconditional stability
1 Introduction
Time integration algorithms are a powerful tool for solving structural dynamics.The accuracy,efficiency,stability,and numerical dissipation have always been important factors when designing a new algorithm or improving an existing algorithm.Based on different design ideas,researchers have developed many types of time integration algorithms,such as theα-algorithms,the composite algorithms,the conserving energy algorithms,and the higher-order algorithms.
To introduce algorithmic dissipation as well as maintain second-order accuracy,theα-algorithms [1-3] like the HHT-αalgorithm,the three-parameter algorithm were developed.By introducing additional parameters in motion equations,theα-algorithms can achieve this goal.Algorithmic dissipation is beneficial to filtering out high-frequency modes and improving stability of time integration algorithms in solving nonlinear systems.However,suchα-algorithms with algorithmic dissipation cause more amplitude and phase errors in the low-frequency region compared to non-dissipative algorithms [4],such as the trapezoidal rule and the central difference algorithm.
To improve low-frequency accuracy of theα-algorithms,multi-sub-step composite algorithms were developed.The composite concepts first appeared in Bank et al.’s work [5],and they developed a two-sub-step algorithm where the trapezoidal rule and the backward difference formula were combined in a time step.Afterwards,this work was extended to the structural dynamics systems by Bathe in 2005 [6].In Bathe’s work,the trapezoidal rule was used in the first-sub-step to maintain low-frequency accuracy as much as possible and the second-sub-step adopted backward difference formula to filter out high-frequency mode contribution.Motivated by these works,some composite algorithms with better numerical properties were proposed in the last two decades,such as the two-sub-step algorithms [7-9],the three-sub-step algorithms [10-15] and the four-sub-step algorithms [13,14].
To solve nonlinear systems,conserving energy algorithms were developed.Different fromα-algorithms and composite algorithms,the construction of conserving energy algorithms is based on the energy principle [16].Most conserving energy algorithms [17-22] can handle the geometric nonlinearity problems and one [23] can deal with the systems including geometric nonlinearity and damping nonlinearity.
To satisfy the pursuit for high accurate solutions,higher-order algorithms [24-32] were developed.The series algorithms,such as the Taylor series algorithm and the Lie series algorithm,are classical higher-order algorithms,which cannot be unconditionally stable when the accuracy order is more than two [25].For keeping higher-order accuracy and improving stability,the multi-stages implicit Runge-Kutta algorithm [26],the weighted-residual method-based algorithms [27,28] and the differential quadrature algorithms [29-31] were proposed.Compared to second-order accurate algorithms,higher-order algorithms can use larger time step size and have advantages in long-term tracking.In 2017,the higher-order algorithms based on the weighted residual method proposed by Kim et al.[28] have thenth-order (n=1,2,3,...) accuracy and unconditional stability with controllable algorithmic dissipation,but the algorithms’stability for nonlinear problems needs to be improved.
As can be seen from above review that (1) there are no multi-sub-step time integration algorithms that have higher-order accuracy,unconditional stability and controllable dissipation;(2) the designs of existing time integration algorithms mainly take accuracy,stability and dissipation into account rather than the properties of dynamic systems.
In this context,this work is to construct a two sub-step higher-order algorithm based on the Kim’s work [28].In the proposed algorithm,a time step [tk,tk+h] is divided into two sub-steps,[tk,tk+γ h] and [tk+γ h,tk+h].Both sub-steps employ the Kim scheme with two collocation points.To obtain better performance,two approaches are provided for determining the parameterγ.The first one is to maximize low-frequency accuracy,in which the value ofγis determined by∂PE(γ)/∂γ=0 where PE denotes percentage period elongation [33].The second is for quickly eliminating high-frequency contribution,and the algorithm with suchγcan perform better in the rigid-flexible coupling and wave propagation systems.
The rest of the paper is organized as follows.Section 2 presents the formulations of the proposed two sub-step algorithm and the determination method of the parameterγ.The numerical properties of the proposed algorithm are discussed in Section 3.Numerical comparisons are provided in Section 4.Finally,the conclusions are drawn in Section 5.
2 The Two Sub-Step Higher-Order Algorithm
This section gives the formulations of the proposed algorithm,in which a time step [tk,tk+h]is divided into two sub-steps as [tk,tk+γ h] and [tk+γ h,tk+h] wherehstands for the time step size.
2.1 The First Sub-Step Formulations
By using the Lagrange interpolation functionsψit(i=0,1,2),the displacementut,velocityvt,and accelerationatin the first sub-step are expressed as

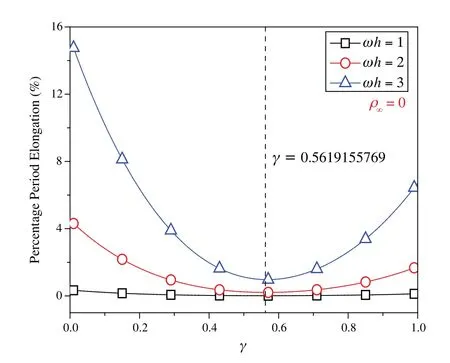
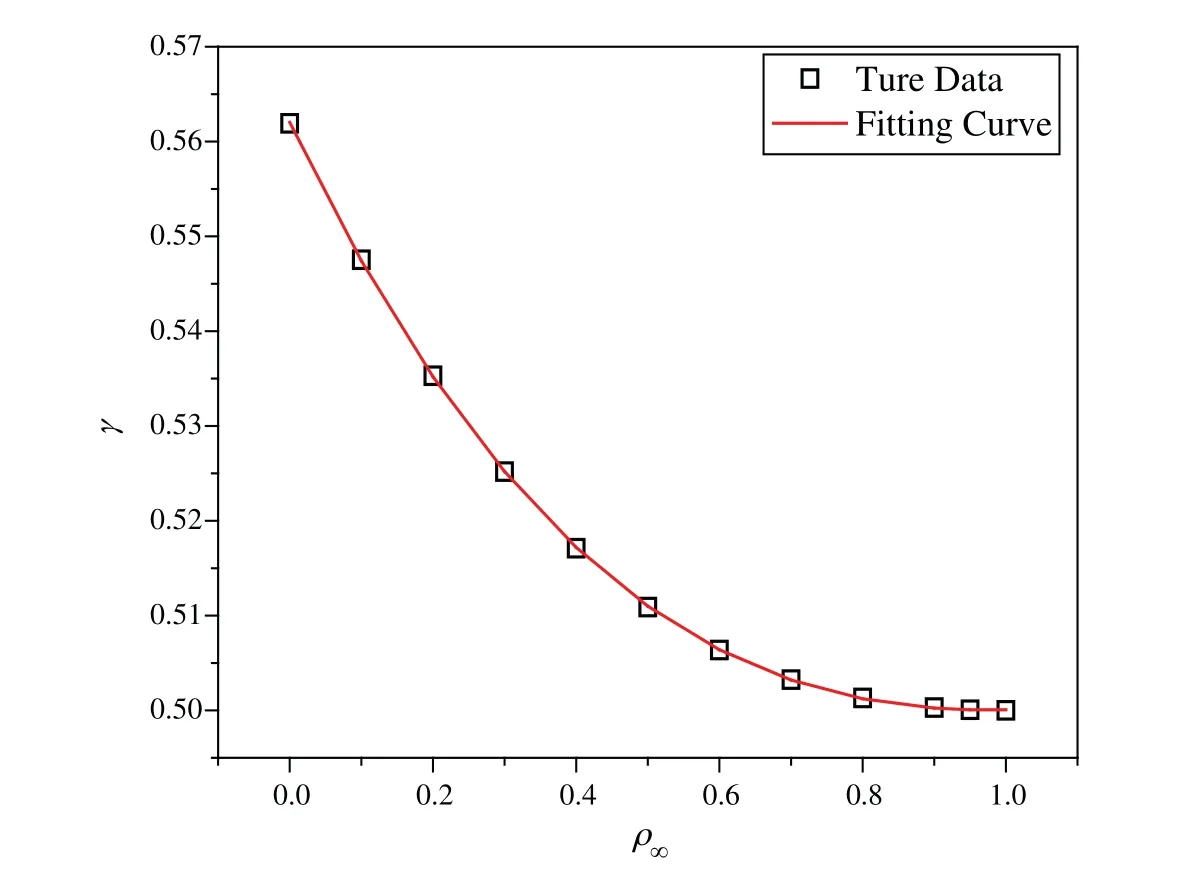
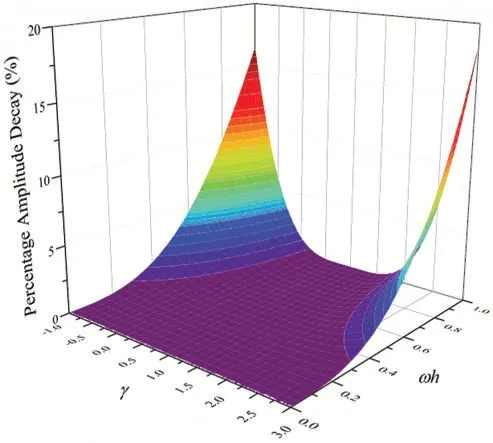
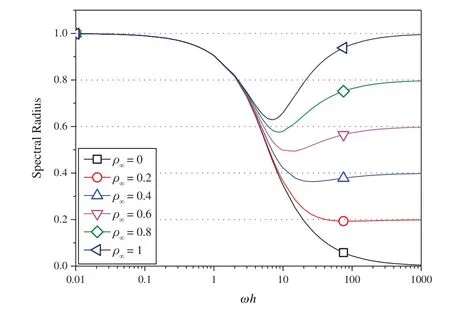
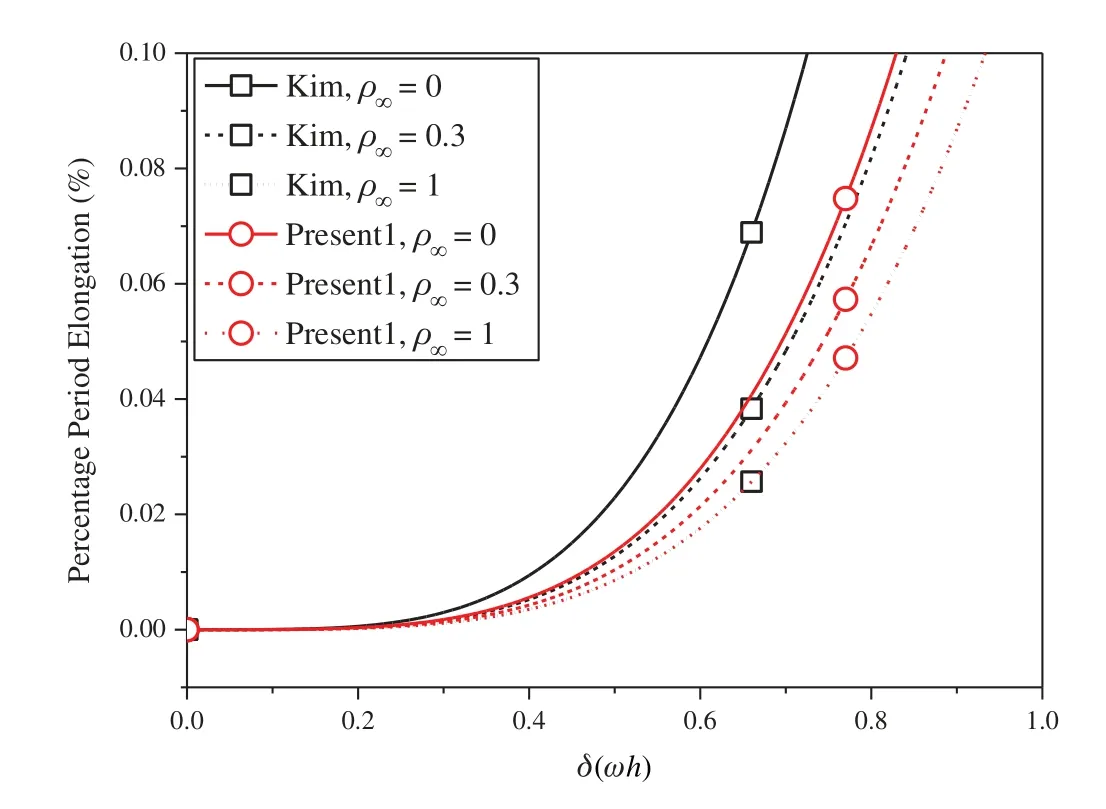
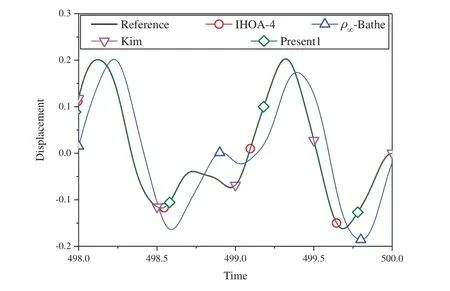
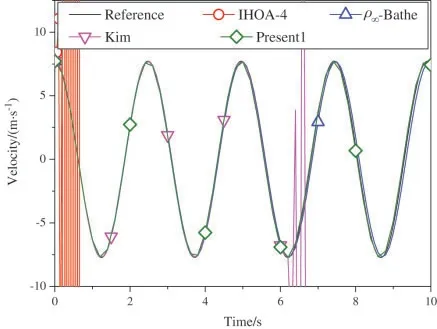
wheretk The displacement,velocity,and acceleration vectors shown in Eqs.(1)-(3) are independent of each other,so two residuals are introduced to describe the velocity-displacement relationship and the acceleration-velocity relationship.The two residuals have the forms as For exact solutions,r1tandr2tare equal to zero.To achieve accurate approximate solutions,here the residualsr1tandr2tare minimized with the following weighted equations as whereτ=t−tk wτis the weighting function.Substituting Eqs.(1)-(3) into Eqs.(7) and (8) leads to the velocity-displacement and the acceleration-velocity relationships in matrix form as whereαij(i,j=1,2),βi(i=1,2),andηi(i=1,2) are all the functions ofθ11andθ12which are where the superscript ‘1’represents the first sub-step,andθ11andθ12can be determined by maximizing the order of accuracy.For this end,consider a single degree-of-freedom system as follows whereξandωdenote the physical damping ratio and natural frequency respectively.In terms of the Eqs.(9) and (10) and for this simple system (12),one can obtain a recursive formulation for first sub-step as whereAis the transfer matrix.The order of accuracy can be designed with the help of local truncation errorσ[33],of which the definition is whereA1=tr(A)andA2=det(A),which are the functions ofθ11andθ12.Ifσ=wherel>0,the method islth-order accurate.Through the Taylor series expansion of displacement att=tk,the explicit expressions ofσcan be obtained as It follows that the first sub-step method is at least second-order accurate and is fourth-order accurate ifθ11=1/2 andFortunately,the spectral radiusρ(A)is equal to 1 whenθ11=1/2 andθ12=1/3.With the relations between (θ11,θ12) and (αij,βi,ηi),one can have For obtaining the unknown vectorsutk+γh,vtk+γh,andatk+γhin the first-sub-step,we consider the following equilibrium equations at the time nodes oftk+γ h/2 andtk+γ h,which have the forms as whereM,CandKare the mass,damping and stiffness matrices;Ris the external load vector.Substituting Eqs.(9) and (10) into Eq.(17) yieldsutk+γhas The above effective stiffness matrixand the effective external load vectorhave the forms as where Then the unknown vectorsutk+γh/2can be obtained as Then,by substitutingutk+γh/2andutk+γhinto Eqs.(9) and (10),one can arrive atvtk+γh,andatk+γh.Andutk+γh,vtk+γh,andatk+γhare the initial conditions of the second sub-step.It is noteworthy that the weighted residual method is a common way in the construction of time integration algorithms.It can be seen from Eqs.(5)-(7) that in the present algorithm,the inherent relations between displacement,velocity,and acceleration are only satisfied in a weak form,but the equilibrium equations are satisfied strictly at discrete points,as shown in Eq.(17). As in the first sub-step,ut,vtandatwithintk+γ h where The velocity-displacement and acceleration-velocity relationships have the matrix forms as where,,(i,j=1,2) are the functions ofθ12andθ22.For the system (12),one can also obtain a recursive formulation like Eq.(13),as whereBis the transfer matrix.Also,according to local truncation error analysis,we can find a relationship ofθ21andθ22as which makes the second sub-step method third-order accurate.In terms of the spectral radius ofB,the following relation can be achieved as Then the parameterρ∞is introduced to control the damping of the present algorithm.By using Eqs.(29) and (30),all free parameters in the second sub-step can be explicitly expressed in terms ofρ∞as With these parameters,the method for the second sub-step is unconditionally stable.To calculate the results attk+h,we take the equilibrium equations attk+(1+γ)h/2 andtk+hinto account as Substituting Eqs.(26) and (27) into Eq.(32) leads to the displacementutk+has The effective stiffness matrix ˆK2and the effective external load vector ˆR2are where and the displacementutk+(1+γ)h/2can be obtained by By insertingutk+(1+γ)h/2andutk+hinto Eqs.(26) and (27),we can achievevtk+h,andatk+h. This sub-section aims to present two approaches for determining the last free parameterγ,the ratio of the first sub-step size and the entire step size. 2.3.1 Approach 1 The first approach is to preserve low-frequency mode contribution as much as possible.To reach this end,the value ofγis determined by minimizing percentage period error.Since the explicit relation amongγ,ρ∞and the phase elongation is complex,the optimalγfor someρ∞are listed in Tab.1.For clearer showing whether or not these values ofγmake the phase error minimum,Figs.1 and 2 show the percentage amplitude decay and the period elongationvs.γforρ∞=0,and Figs.3 and 4 display the results forρ∞=0.5.It can be seen that these values ofγcan really minimize period elongations,noting that at the minimum point the amplitude decay is also close to the minimum.To simply obtain the optimalγfor anyρ∞,a fitting algebraic relationship betweenρ∞and the optimalγis provided as Table 1:The relationships between the optimal γ and ρ∞ Fig.5 shows the fitted and true values ofγ.The proposed algorithm using theγin Eq.(37),denoted by ‘Present 1’in this paper,is recommended for most dynamics problems. Figure 1:Percentage amplitude decay vs.γ (ρ∞=0,ξ=0) Figure 2:Percentage period elongation vs.γ (ρ∞=0,ξ=0) Figure 3:Percentage amplitude decay vs.γ (ρ∞=0.5,ξ=0) Figure 4:Percentage period elongation vs.γ (ρ∞=0.5,ξ=0) Figure 5:The comparisons between the fitted values and the true values 2.3.2 Approach 2 For rigid-flexible coupling and wave propagation problems,time integration algorithms that can quickly damp out high-frequency effects are expected.To achieve such a capability,the parameterγcan be determined by the following second approach. Fig.6 shows the variations of the percentage amplitude decay of the proposed algorithm withγandωhfor the case ofρ∞=0,and the result ofρ∞=0.5 is provided in Fig.7.It can be seen that the percentage amplitude decay curves are symmetric aboutγ=1 for any values ofωh.Fig.8 shows the spectral radiusvs.ωhfor several givenγ,indicating that the larger amount of numerical dissipation can be obtained in the low-frequency range with a larger |γ|. Figure 6:The variations of percentage amplitude decay with γ and ωh (ρ∞=0) As is well known,most time integration algorithms with controllable dissipation possess the biggest amount of dissipation whenρ∞=0.It can be seen from Figs.6-8 that the amount of dissipation can be improved further by adjusting the values ofγfor the proposed algorithm.For ensuring the accuracy of low-frequency response,the value ofγsatisfyingρ=0.7~0.8 is suggested,refer to Fig.8.The proposed algorithm using the value ofγdetermined by this approach is denoted by ‘Present 2’in the numerical comparisons in Section 4. Figure 7:The variations of percentage amplitude decay with γ and ωh (ρ∞=0.5) Figure 8:Spectral radius vs.ωh and γ (ρ∞=0):(a) ωh ∈ [0.1,100];(b) ωh=0.1,0.2,0.4,0.6,1,4,10,100 After determiningγ,the construction of the present algorithm is completed,and its flowchart and step-by-step implementing procedure are presented in Fig.9 and Tab.2 respectively.Using the Newton iteration method,the proposed algorithm is also applicable to the general nonlinear dynamics as whereN(vt,ut) is the nonlinear resilience force. Figure 9:Flowchart of the proposed algorithm for linear systems Table 2:Step-by-step implementing procedure of the proposed algorithm for linear systems Table 2(continued). This section is to discuss the proposed algorithm’s properties,including efficiency,stability,dissipation,accuracy,and convergence rates.In this work,the present algorithm is compared with the single-step fourth-order Kim method [28],the single-step fourth-order IHOA-4 [32],and the two-sub-step second-orderρ∞-Bathe method [7].The accuracy of different types of algorithms should be compared under the same computational cost.In terms of the number of times the equilibrium equation is used in a time step,the time step sizes of these algorithms should satisfy 4h(IHOA−4)=2h(ρ∞−Bathe)=2h(Kim)=h(Present) (indicating that the step size of IHOA-4 is a quarter of the step size of the present method,for example) to ensure that the accuracy comparison is conducted under roughly equal computational costs. In general,a SDOF system like (12) is used to examine the properties of a time integration algorithm for linear systems.The spectral analysis of Present 2 have been presented Section 2.3.2,so this section mainly discusses the numerical properties of the ‘Present 1’.Figs.10-12 show the spectral radiusvs.ωhand Figs.13 and 14 show the percentage amplitude decay and period elongationvs.δ(ωh) whereδ(ωh)= (ωh)/n(nstands for the number of times the equilibrium equation is used in a time element),keeping same computational costs.It can be seen from Figs.10-12 that the present algorithm is unconditionally stable for undamped and damped systems,and its numerical dissipation can be exactly and smoothly controlled byρ∞.Figs.13 and 14 illustrate that (1) ifρ∞=1,Present 1 almost has the same amplitude and phase accuracy as the Kim algorithm;(2) ifρ∞/=1,Present 1 is more accurate than the Kim algorithm.Since the amplitude errors of them are all zero whenρ∞=1,the relevant results are not plotted in Fig.13. Figure 10:Spectral radius vs.ωh for Present 1 (ξ=0) Figure 11:Spectral radius vs.ωh for Present 1 (ξ=0.1) Figure 12:Spectral radius vs.ωh for Present 1 (ξ=0.2) Figure 13:Percentage amplitude decay vs.δ(ωh) (ξ=0) Figure 14:Percentage period elongation vs.δ(ωh) (ξ=0) The convergence rates of the proposed algorithm are checked in this section.Consider a SDOF system as whereω=2,r(t)=sint,and the initial displacement and velocity are zero.The decrease rates of absolute errors as the step size decreases are defined as the convergence rates,and displacement,velocity and acceleration may have different convergence rates.Theρ∞-Bathe algorithm [7] is second-order accurate,so its results are plotted here as a reference.The value of the parameterγhas no effect on algorithmic order,refer to Eq.(15),so only the results of Present 1 are shown here. The undamped case is considered first.Fig.15 shows the absolute errors of displacement,velocity,and acceleration.It can be seen that the proposed algorithm and the Kim algorithm are both fourth-order accurate whenρ∞=1,and they are both third-order accurate otherwise;the present algorithm is more accurate than the Kim algorithm when 0≤ρ∞<1. Figure 15:Convergence rates of the undamped system (ξ=0) For the damped case,ξ=0.1 is used.It can be seen from Fig.16 that the proposed algorithm is still fourth-order accurate whenρ∞=1 and third-order accurate when 0≤ρ∞<1. Figure 16:Percentage period elongation vs.δ(ωh) (ξ=0.1) To verify the performance of the proposed algorithm,some numerical experiments are conducted here.The proposed algorithm is compared with the Kim algorithm [28],the IHOA-4 [32],and theρ∞-Bathe algorithm [7].In all simulations,the time step size of the IHOA-4 is provided and the sizes of other algorithms can be determined by the relations of 4h(IHOA−4)=2h(ρ∞−Bathe)=2h(Kim)=h(Present). In this example,consider a linear bi-material bar subjected to a harmonic displacement excitation at the left end [28],as shown in Fig.17.The motion equation of the bi-material bar is with the initial and boundary conditions of The dimensionless mass density,sectional area and length are assumed asρ=1,A=1 andL=1 respectively,and the elasticity modulus isE(x)=E1for 0≤x≤L/2 andE(x)=E2forL/2 Figure 17:A bi-material bar with a harmonic displacement excitation at the left end 4.1.1 The First Case(E1=10and E2=1) This case is used to test the performance of the higher-order accurate algorithms for long-term tracking.The step sizeh=0.005 ≈Tmin/6 whereTmin≈0.0344138,and the reference solutions are achieved via the mode superposition method.For long-term simulations,numerical dissipation is not expected,soρ∞=1 is employed in all algorithms.Figs.18-20 illustrate the results of the middle point of the bar for the time interval [498,500],where one can see that the second-order accurateρ∞-Bathe algorithm have obvious errors and other fourth-order accurate algorithms’results agree well with the reference solution. Figure 18:The displacement of the middle point for the first case Figure 19:The velocity of the middle point for the first case Figure 20:The acceleration of the middle point for the first case 4.1.2 The Second Case(E1=5000and E2=1) The second case is designed to show the better performance of numerical dissipation of the proposed algorithm over other higher-order algorithms.The time step sizeh=0.005 is used,andρ∞=0 is employed.To better handle the present rigid-flexible coupling problem,the parameterγof the proposed algorithm is determined byApproach 2.It can be seen from Figs.21-23 that:(1) the proposed algorithm can eliminate high-frequency effects without introducing excessive errors;(2) the Kim algorithm has obvious numerical oscillations;(3) the IHOA-4 loses stability due to its conditional stability.To make the figure clearer,the acceleration results of the IHOA-4 are omitted in Fig.22. Figure 21:The displacement of the middle point for the second case Figure 22:The velocity of the middle point for the second case Figure 23:The acceleration of the middle point for the second case Moreover,the CPU time required by different algorithms in this example are presented in Tab.3 where one can observe that the computational costs of different algorithms are almost equal when the step sizes satisfy the relation 4h(IHOA−4)=2h(ρ∞−Bathe)=2h(Kim)=h(Present). Table 3:CPUs of different time integration algorithms in Example 1 Consider a nonlinear pendulum system [17] pinned at the top and free at the bottom,as shown in Fig.24.The material parametersEA=1010N,ρA=6.57 kg/m and the lengthl0=3.0443 m are adopted,and the rotation of the pendulum is started by an initial tangential velocity ofv0=7.72 m/s at the free end.Since the axial stiffness is huge,the motion of the pendulum is like a rigid rotation.A linear truss element is used to model the pendulum,so the system has two DOFs. Figure 24:Truss model of the rigid pendulum The step sizeh=0.05 s,andρ∞=0 is used.The results of theρ∞-Bathe algorithm with an extremely small time step size serve as the reference solutions.Figs.25-27 show the results of the free end in thexdirection within [0,10 s].It can be seen that the IHOA-4 and the Kim algorithm fail.In fact,this simple problem has also defeated some other famous algorithms,such as the trapezoidal rule.Also,we can find that theρ∞-Bathe algorithm exhibits phase lag. Figure 25:Displacement of the free end in the horizontal direction Figure 26:Velocity of the free end in the horizontal direction Figure 27:Acceleration of the free end in the horizontal direction As shown in Fig.28,in this example a two-story shear building is considered,which has two degrees of freedom.The lumped masses of the bottom and the top floors aremb=103kg andmt=104kg,respectively.The nonlinear stiffness for each story is wherek0is the initial stiffness and Δurepresents the story drift.For the bottom story,k0=108N/m,and thek0=105N/m is for the top story.Two stores are subjected to the same the external forcef1=f2=10sin(t).The coefficientsα=100 andα=−0.1 are used for the bottom and top stories respectively.The step sizeh=0.0625 s,andρ∞=0 is used.The reference solution is achieved through theρ∞-Bathe algorithm with a much smaller step size.Figs.29-31 provide the results of the top story.One can see that:(1) The non-dissipative IHOA-4 loses stability;(2)Theρ∞-Bathe algorithm and the Kim algorithm have larger errors than the present method. Figure 28:Two-story shear building Figure 29:Displacement of the top story Figure 30:Velocity of the top story Figure 31:Acceleration of the top story Based on the single-step Kim algorithm,this work proposed a two sub-step higher-order time integration algorithm with unconditional stability and controllable dissipation.A non-dissipative fourth-order accurate scheme is used in the first sub-step,and a third-order accurate scheme with controllable dissipation is used in the second-sub-step. As to the determination of the parameterγ,the ratio between the first-sub-step size and the entire step size,this work provided two approaches for achieving different goals.One approach maximizes low-frequency accuracy and the other can quickly damp out high-frequency mode effects. The numerical properties and simulations showed that the present two sub-step algorithm has accuracy,dissipation,and stability advantages over the Kim algorithm and theρ∞-Bathe algorithm. Funding Statement:This work was supported by the National Natural Science Foundation of China (Grant Numbers 11872090,11672019 and 11472035). Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.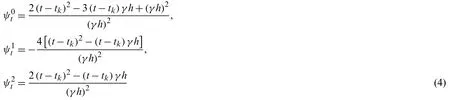







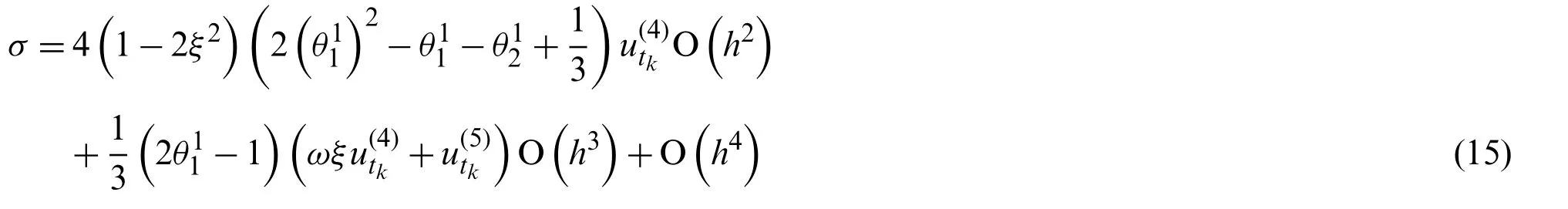

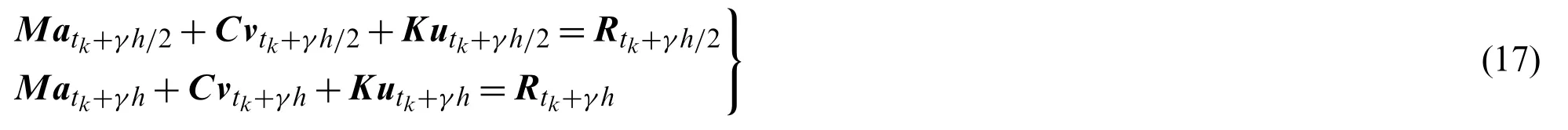




2.2 The Second-Sub-Step Formulations


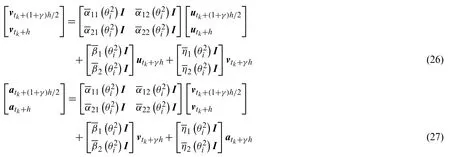



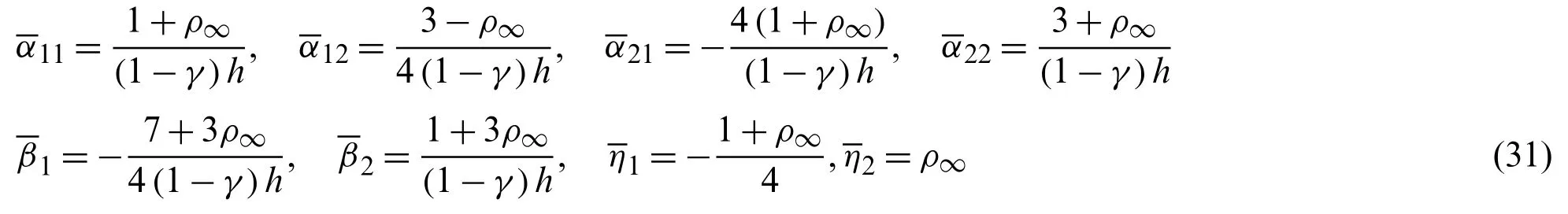



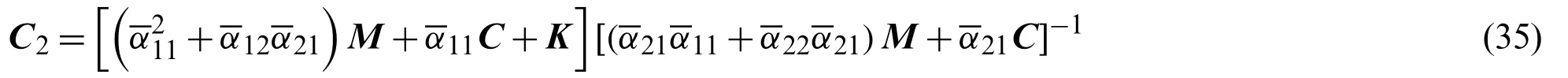

2.3 Determination of the Parameter γ










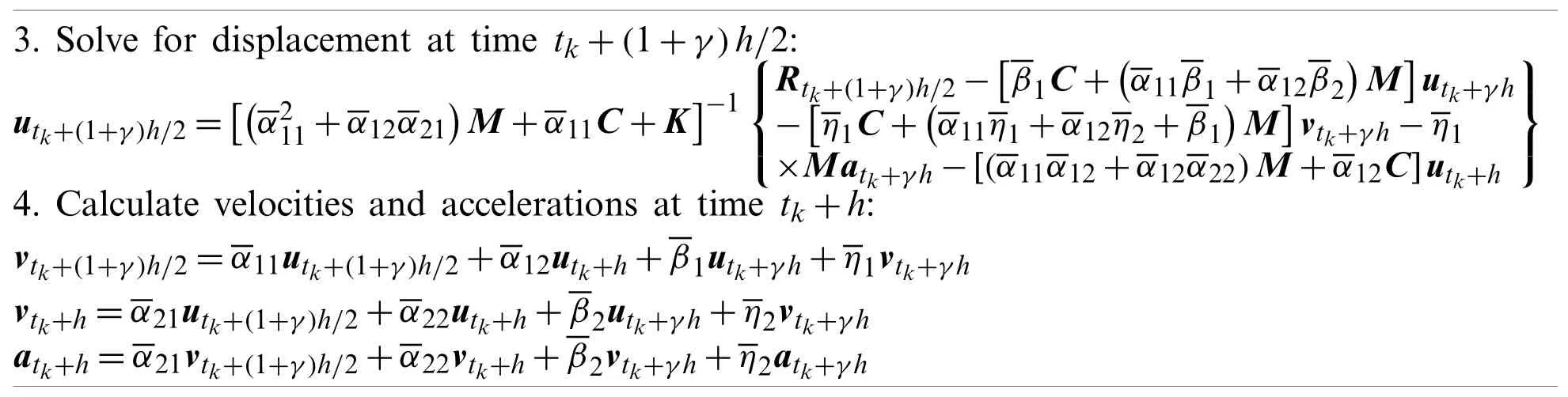
3 Properties Analysis
3.1 Stability,Dissipation and Accuracy



3.2 Convergence Rates


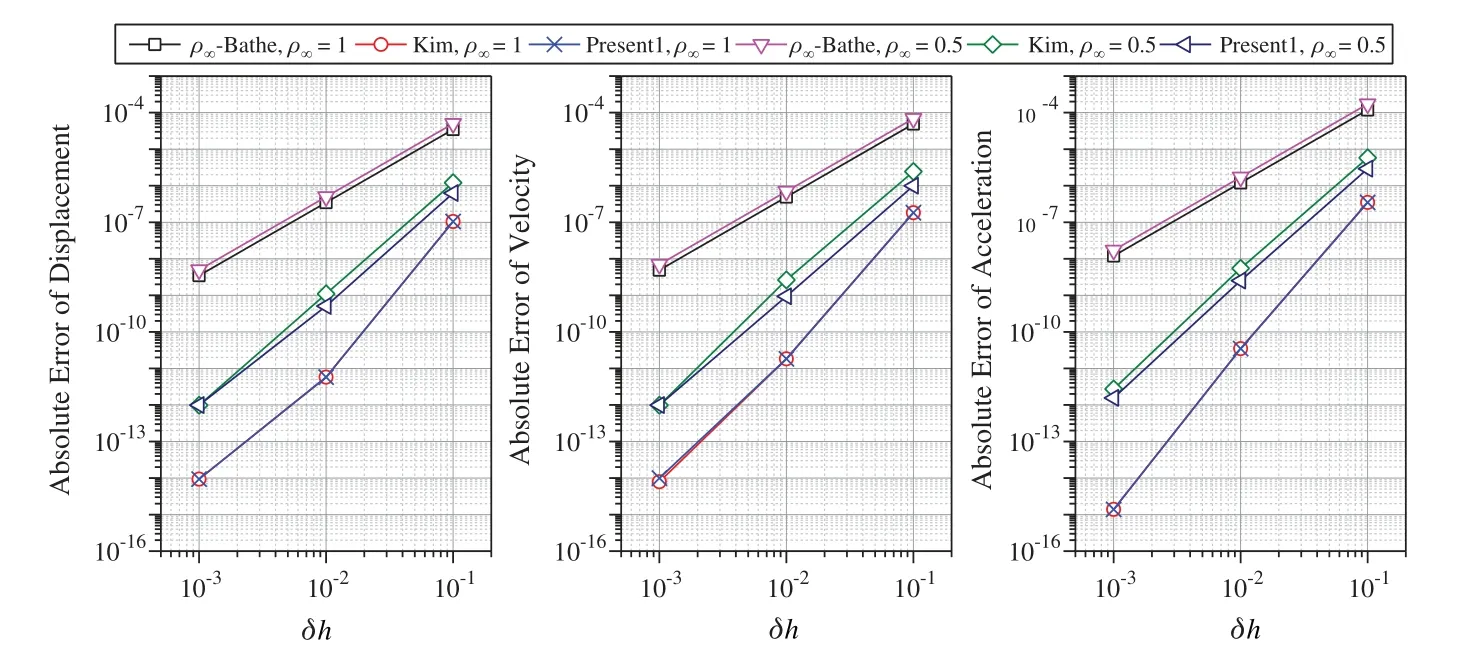
4 Numerical Experiments
4.1 Bi-Material Bar Problem







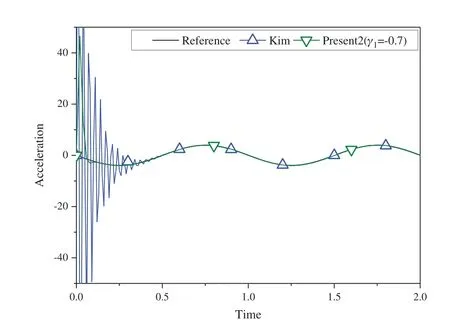

4.2 Rigid Pendulum System



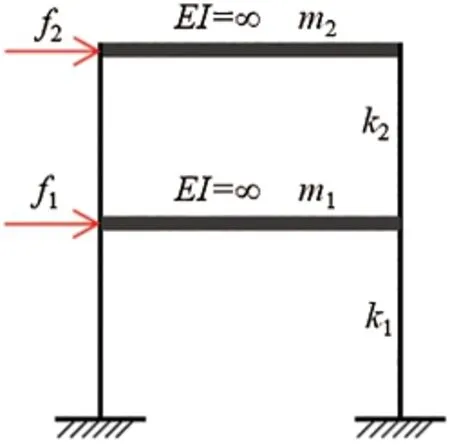
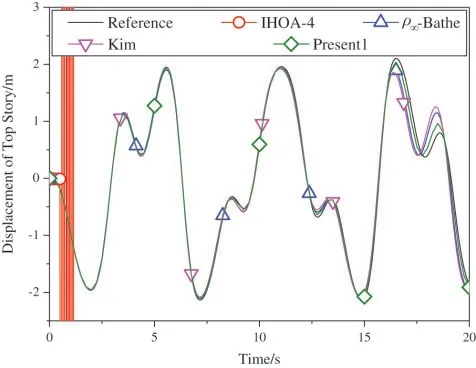
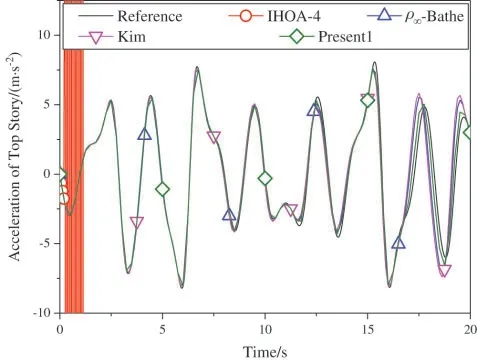
4.3 The Two-Story Shear Building


5 Conclusions
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- E-Commerce Supply Chain Process Optimization Based on Whole-Process Sharing of Internet of Things Identification Technology
- Nonlinear Thermal Buoyancy on Ferromagnetic Liquid Stream Over a Radiated Elastic Surface with Non Fourier Heat Flux
- Shear Induced Seepage and Heat Transfer Evolution in a Single-Fractured Hot-Dry-Rock
- Impacts of Disk Rock Sample Geometric Dimensions on Shear Fracture Behavior in a Punch Shear Test
- An Uncertainty Analysis Method for Artillery Dynamics with Hybrid Stochastic and Interval Parameters
- Stability and Bifurcation of a Prey-Predator System with Additional Food and Two Discrete Delays
