联合V2X通信和最小跳数距离的车辆定位方法*

刘 冲,张月霞

(北京信息科技大学 通信工程学院，北京 100101)

0 引 言

智能交通是城市道路交通系统的重要发展方向，其将机器学习、大数据等多种先进技术融入交通运输系统，在交通运输、交通安全、网络安全、交通拥堵、智能化业务等方面发挥着重要作用[1-2]。车辆高精度定位技术是智能交通的基础，但以GPS[3]为代表的全球导航卫星系统(Global Navigation Satellite System,GNSS)在隧道、山区、立交桥下、高楼密集的城市等区域无法提供连续且准确的位置服务，致其难以满足实时性和安全性较高的车辆应用[4]。随着智能交通系统的不断发展，基于车联网的应用日益丰富。车联网通过V2X通信技术实现车与车(Vehicle to Vehicle,V2V)、车与路侧单元(Vehicle to Road unit,V2R)之间的高效通信，这为进一步提升车辆定位性能提供了可能[5]。车辆短程通信技术(Dedicated Short Range Communication，DSRC)被视为V2X系统的主要实现方法[6]，待定位车辆中的车载单元(On Broad Unit，OBU)可通过DSRC技术接收通信范围内的路侧单元 (Road Side Unit，RSU)或OBU的信息，从而解算自身坐标[7]。

现阶段很多研究致力于利用V2X通信实现车辆高精度定位。文献[8]提出了一种基于机器学习的车辆定位方法，在采集点密度较高情况下可以取得较高定位精度，但其准备阶段会耗费大量时间去构建信号强度库，固不适宜大规模采用。文献[9]提出了一种基于加权置心的优化加权定位(Optimized Weighted Location,OWL)方法，待定位车辆通过距离、信号干扰噪声比、相对方向等信息对传统质心算法进行加权处理，从而提高了传统质心算法的定位精度。该方法具有计算简单的优势，但定位精度偏低。文献[10]提出了一种基于到达角度(Direction of Arrival,DOA)和V2X通信的车辆定位方法，待定位车辆从辅助RSU和辅助车辆的广播信息中解算来波角度，并利用来波角度的正切值构建包含位置的方程组解算车辆坐标。该方法虽然可以取得较高的定位精度，但基于DOA的车辆定位方法需要在每个车辆中安装全向天线，这无疑加大了成本开支。文献[11]对解算车辆坐标的传统三边定位算法进行了修正，把车辆位置估计转换为非线性规划问题，并结合外部罚函数和尺度变化进行求解，最后将残差定权引入定位模型，避免了单一模型带来的偶然误差。该算法一定程度上提高了定位精度，但复杂的迭代过程无疑增加了车辆的负担。

在实际情况中，由于预算、能耗等多方面因素影响,RSU和已知位置的车辆所组成的辅助节点分布稀疏。而上述定位方法中车辆只有在辅助节点的通信范围内才能对接收信息作出处理，这往往会造成由于辅助节点数量不足导致定位无法完成的情况。以二维场景下三边定位算法为例，这要求待定位车辆需同时位于三个辅助节点的通信范围内才可完成定位，这通常难以保证。对此，本文提出了一种联合V2X通信和最小跳数距离(Minimum Hop Distance-V2X，MHD-V2X)的车辆定位方法。各辅助节点与其通信范围外车辆之间的相对距离用最小跳数距离进行估算，并通过校正节点对估算误差进行修正。在解算车辆位置坐标时，综合考虑距离、辅助节点类型对定位误差的影响，利用加权最小二乘法解算位置方程组，改善定位精度。该方法充分利用了网络中辅助节点信息，改善了传统测距受通信距离约束的限制的局限，提高了定位精度。

1 V2X定位原理

在基于V2X[12]的定位中，若干RSU规则部署于道路两侧，其坐标通过更精确的测量方式预先测定得出。网络中的车辆可分为已知坐标车辆和未知坐标车辆。已知坐标车辆坐标可由GPS、V2X及MHD-V2X等定位方法实时提供。已知坐标车辆和RSU共同构成网络中的辅助节点，其通信范围分别为r和R。未知坐标车辆为网络中的未知节点。辅助节点以周期T在其通信范围内进行位置广播，其中包含自身标识和位置信息。未知节点中提出位置请求的节点为待定位节点，待定位节点在发起位置请求后，需接收辅助节点的位置广播信息并从中解算出自身位置坐标。V2X定位示意图如图1所示。

图1 V2X定位示意图

设车辆V0为待定位节点，忽略高度上的变化，理想情况下V0的位置坐标可通过求解方程组(1)获得：

(1)

式中：(x,y)为待定位车辆V0的位置坐标，(xn,yn)为第n个辅助节点的位置坐标，dn为V0到第n个辅助节点的相对距离。在二维场景下当n≥3时，可通过最小二乘法、Taylor级数法、最大似然估计法等对(x,y)的值进行求解。

2 MHD-V2X定位方法

2.1 基于最小跳距的距离估计

在稀疏辅助节点环境下，由于通信距离的限制，待定位节点难以在短时间内接收到足够的辅助节点信息，导致定位无法完成。但如果可以利用节点对广播信息的转发从而对辅助节点到其通信范围外待定位节点间的相对距离进行合理的估计，那么便可对网络中的辅助节点进行充分利用，提升定位性能。

在MHD-V2X定位方法中，规定网络各车辆节点可对接收到的位置广播信息在通信范围r内进行转发，直至达到转发次数上限N。网络中的位置广播LB应包含如下信息：

LB=[hop,{id},Locs,Ps,{d}] 。

(2)

定义源节点为一条广播路径中广播的发起节点，其中跳数hop为广播自源节点至前节点历经的传播次数，设其初值为0，每当节点对位置广播进行转发时修改hop=hop+1；有序集合 {id}中元素为位置广播自源节点至当前节点所历经节点标识的有序排列，各节点在收到位置广播后将自身标识加至其中；Locs为当前广播中源节点的位置坐标；Ps为当前节点发射信号功率，该值随hop值的增加而被不断更新；有序集合{d}中元素表示集合{id}中两相邻节点间的相对距离，其数值可由如下路损模型计算得出:

(3)

式中：Ps、Pr分别为相邻两节点间的发射功率和接收功率，λ为信号波长，d为节点间的相对距离，Gs和Gr是天线增益，β为系统损耗因子。通常情况下设Gs=Gr=β=1为默认值[9]。波长λ可由下式获得：

(4)

式中：C是真空中光速,f为信号传播的频率。

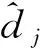
(5)

用最小跳数距离近似等于相对距离，即

(6)

则V0和Aj间存在如下约束：

(7)

式中：(x,y)为待定位车辆V0位置坐标，(xj,yj)为辅助节点Aj位置坐标。

2.2 基于校正节点的误差补偿

在2.1节中利用辅助节点与其通信范围外待定位节点间的最小跳数距离去代替相对距离，但由于最小跳数距离为折线段，与相对距离间存在较大误差，称这种误差为最小跳数误差，V0与Aj间的最小跳数误差ej可表示如下:

(8)

为了对该误差进行补偿，将网络中的辅助节点视为待定位节点，并用2.1节中的方法不断计算自身与跳数限制N内其余辅助节点间的最小跳数距离。由于辅助节点位置坐标已知，故很容易求得辅助节点间的相对距离，从而计算最小跳数误差。辅助节点以周期T进行误差广播，接收到误差广播的节点对hop值进行更新并转播，直至达到跳数上限N。网络中的误差广播EB应包含如下信息：

EB=[hop,ids,{erro},{ide},{routemin}] 。

(9)

式中：hop为当前跳数；ids为该条误差广播所对应的源节点标识；有序集合{erro}和{ide}分别为源节点所获取到与其他辅助节点间的最小跳数误差和对应的节点标识；定义最小跳数路径routemin为关于同一源节点到待定位节点的多路广播中拥有最小跳数值的位置广播所对应的传播路径，{routemin}为源节点ids到{ide}中节点间的最小跳数路径有序集合。V0在获取与Aj间的最小跳数距离后，需从各误差广播所对应的源节点中选择一个到Aj的最小跳数路径与V0到Aj的最小跳数路径相似度最高的源节点作为V0到Aj的校正节点，用其到Aj的最小跳数误差代替V0到Aj的最小跳数误差。在此利用杰卡德(Jaccard)相似系数[13]去衡量两组路径的相似程度：

(10)

规定一条路径中两相邻节点构成集合中的一个元素，式(10)含义为路径集合P和路径集合Q的交集在其并集中所占比例。

设Ai为V0到Aj的校正节点，用Ai到Aj的最小跳数误差eij去代替V0到Aj的最小跳数误差ej，即

ej≈eij。

(11)

将式(11)代入式(8)可得

(12)

因此，式(7)可进一步修改为

(x-xj)2+(y-yj)2=dj2。

(13)

2.3 基于加权最小二乘的位置估计

自发起位置请求时刻起的时间间隔Δt内，若待定位车辆可以获取到自身与3个及以上辅助节点间的相对距离则可联立式(1)所示方程组，并利用最小二乘法对其求解。但最小二乘法认为每个方程式的贡献都是等价的,在复杂的车联网环境中很多因素都会导致距离估计变得不准确，为此引入加权最小二乘算法为每一个方程式分配权重，从而进一步提升定位精度。对此主要考虑以下两方面：

(1)距离对定位精度的影响

测距误差会随着待定位节点与辅助节点之间距离的增大而增大，这通常是由接收信号强度指示(Received Signal Strength Indicator,RSSI)测距模型的累计误差和复杂的空间环境所决定的，因此将该部分权值设为两者相对距离的倒数。但该距离是利用校正RSU对最小跳数误差进行补偿得到的，且在估计待定位车辆到不同辅助节点间相对距离时，校正RSU对应的路径相似度也存在着差异。由于路径相似度与估算误差呈正相关趋势，对此设定该项权值为

(14)

式中：J是校正节点所对应的路径相似度值。

(2)辅助节点类型对定位精度的影响

在基于V2X通信的定位模型中存在RSU和已知坐标的车辆两类辅助节点，通常情况下路侧单元坐标由精确的测量方式预先测定，具有较高精度，而车辆的坐标可由多种定位方式实时获得，但坐标精度相对RSU而言较低。利用不同精度的辅助节点对待定位节点进行定位会对定位结果产生一定的影响，对此定义该项权值为辅助节点获取自身坐标方法的置信度，利用均方误差的倒数对置信度进行衡量，则该项权值可表示为

(15)

式中：RMSE(type)表示辅助节点在获取自身坐标时所用定位方法type对应的均方根误差，该值可在指定环境中由公式(16)提前测得：

(16)

式中：m为测量次数；(xi,yi)为定位方法type在第i次测量中的坐标值；(x,y)为节点坐的精确值，其由更高精度测量手段近似得来。

综上所述，用于加权最小二乘法的最终权重值w可表示为

w=αwa+(1-α)wb，0<α<1 。

(17)

式中：影响因子0<α<1，用来权衡wa和wb的侧重度。因此式(1)可继续改写为

(18)

式中：wn为第n个方程式所占权重。将式(18)整理为AX=b形式，其中：

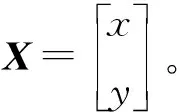
利用最小二乘思想[14]对下式进行最小化处理来计算X的估计值:

F(x)=‖S‖2=‖b-Ax‖ 。

(19)

式中：S为n-1维的误差向量。对F(x)求导并令其为0，可求得未知量X如下：

X=(ATA)-1ATb。

(20)

2.4 MHD-V2X定位流程

MHD-V2X定位方法的流程如图2所示。

图2 MHD-V2X定位方法流程

在网络初始化阶段各辅助节点以周期T进行位置广播及误差广播，网络中的车辆节点可对接收到的广播进行再次转播，直至达到转播上限N。

车辆在提出位置请求后，一方面需从位置广播中解算出辅助节点的位置坐标及自身与辅助节点间的最小跳数距离，另一方面需从误差广播中解算出辅助节点间的最小跳数误差。利用上述信息，可以求得待定位车辆与辅助节点间的相对距离。

若车辆在指定时间内获取到自身与不同辅助节点间的相对距离个数大于等于3，则利用相对距离信息及辅助节点的位置坐标联立式(1)所示方程组，利用2.3节所示方法计算各方程组权重，并结合加权最小二乘法对待定位车辆的坐标进行求解，完成定位；反之，若获取自身与不同辅助节点间相对距离个数小于3，则视为本次定位失败，需重新进行定位。

3 仿真分析

为验证所提法的性能，在双向四车道模型中进行仿真分析，每条车道宽度W=3.5 m，其中RSU交替分布于道路两侧0.5 m处，广播周期T=0.2 s，相邻RSU水平距离1 km；设RSU通信范围R=300 m,车辆通信范围r=30 m，辅助车辆数量占总车辆数量10%，单条车道中车辆密度为ρ(辆/m)，信号传播频率f=5.8 GHz，综合考虑网络开销及定位性能取转发上限N=5，默认通信节点间距离为视距距离。

定位成功率直接影响着定位性能。当待定位车辆发起定位请求后需收到3个辅助节点广播信息时方可完成定位。设Δt=1 s，通过改变RSU间水平距离L及车辆密度ρ，比较本文定位方法与V2X定位方法的定位成功概率，其中Monte Carlo仿真次数为400。仿真结果如图3和图4所示。

图3 V2X定位成功率随L、ρ变化折线

图4 MHD-V2X定位成功率随L、ρ变化折线

由图3和图4可知，两种定位方法的定位成功率与RSU间水平距离L呈正相关，与车辆密度ρ呈负相关。但随着L的增大及ρ的减小，本文所提定位方法定位成功率的下降幅度要远远小于传统V2X定位方法的定位成功下降幅度。综合考虑不同L和ρ的情况，MHD-V2X定位方法与V2X定位方法相比平均定位成功率提高38.6%。其原因在于随着网络中锚节点数量的减小，传统V2X定位方法受通信距离的局限难以在短时间内获得3个辅助节点的广播信息，而本文所提算法通过车辆对广播信息的转发，从而对网络中的锚节点信息进行充分利用，以更大概率完成定位，更具有实用价值。

为进一步验证所提方法的性能，对本文定位方法位精度与其余定位方法进行了仿真比较，单次测量中误差的衡量标准采用式(16)来衡量。设ρ=0.1，L=500，GPS无多径干扰下定位均方根误差5 m，RSU自身位置坐标均方根误差1 m，测距误差是均值为0的高斯白噪声，其方差随通信距离的增加在1～4 m2内线性增长；网络中辅助车辆节点位置坐标来源于理想GPS定位。MHD-VTX定位方法中取影响因子α=0.8，其取值对应平均定位误差如图5所示。

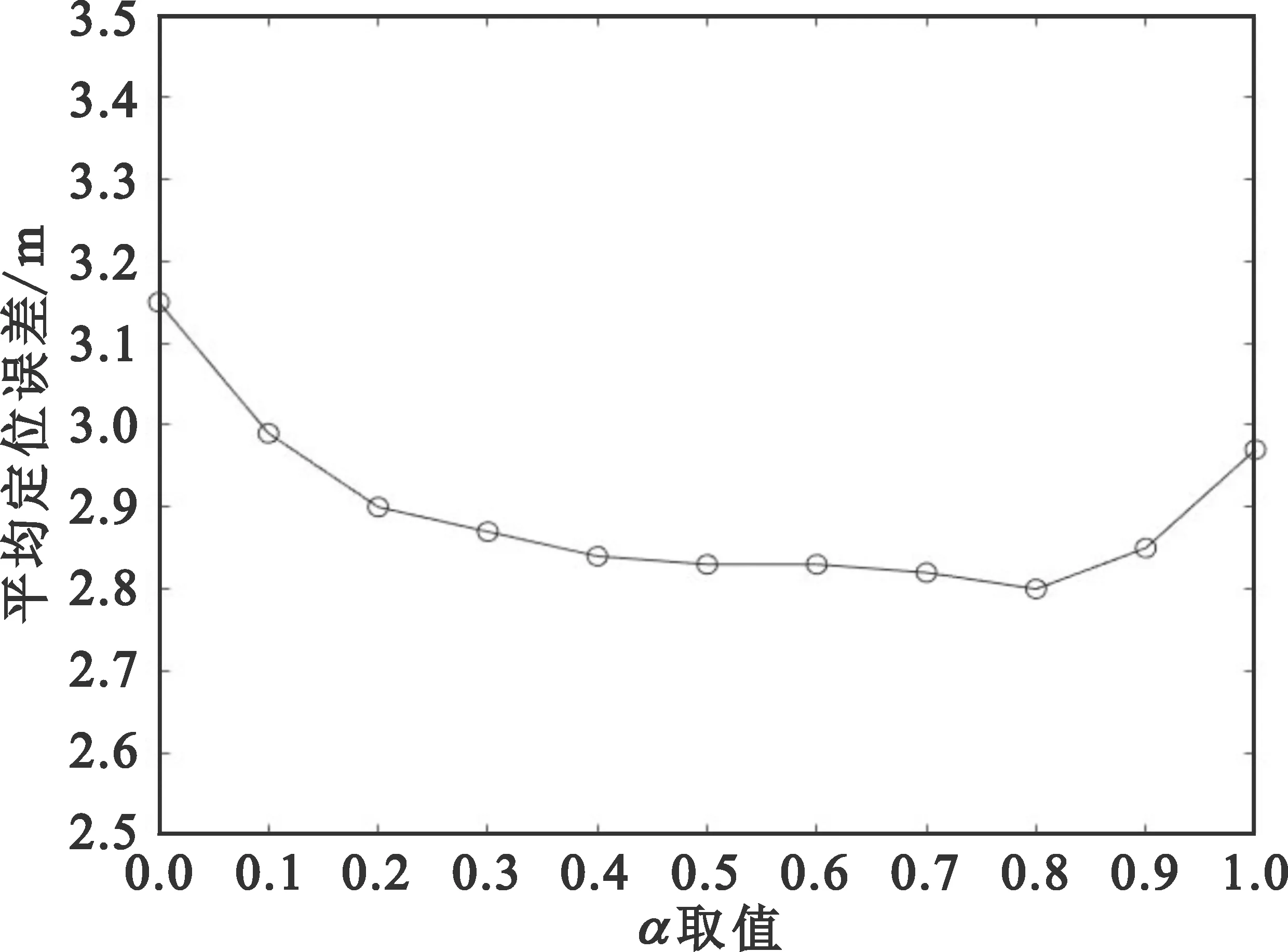
图5 平均定位误差随α变化图

综上所述，对MHD-V2X定位方法、V2X定位方法、GPS定位方法及OWL方法的定位误差进行比较，结果如图6所示。

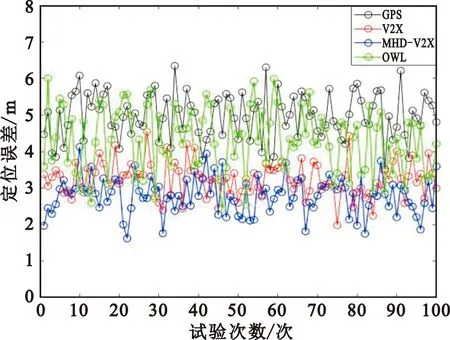
图6 不同定位方法定位误差比较图

由图6可知，在该仿真环境下，单独GPS定位精度在5 m左右，传统V2X定位精度为3.2 m,OWL算法精度为4.3 m,本文所提算法的定位精度可达2.8 m，与GPS、V2X、OWL定位方法相比，本文定位方法定位精度分别提升了50%、12.5%和34.9%。MHD-V2X定位方法具有较高定位精度，原因在于将距离信息及辅助节点类型信息转化为加权二乘法的权值，对误差系数较高的位置方程赋予更高的权重，从而对定位精度进行改善。

在时间复杂度方面，MHD-V2X定位方法和V2X定位方法为平方阶复杂度O(n2)，OWL定位方法为线性阶复杂度O(n)。其主要原因是在解算待定位车辆位置坐标时，加权质心算法比最小二乘算法及加权最小二乘算法具有更低阶的运算量。另外，由于本文所提方法中车辆节点会将辅助节点的信息进行转播，这在一定程度上增加了网络的能耗和开销，但由于所转发内容仅仅为距离、标识、信号强度等基本字节信息，故不会对未来车辆网通信负载造成较大负担。

4 结束语

本文提出利用最小跳数距离和V2X通信相结合的方法实现车辆的高精度定位。在本文方法中，辅助节点的信息可以传达至通信范围外的待定位车辆，从而使待定位车辆可以获取更多的辅助节点信息，增加定位成功率。同时，综合考虑距离、辅助节点类型等因素的影响，利用加权二乘法求解定位方程组，以此来提升定位精度。仿真结果表明，本文所提定位方法在定位成功率及定位精度方面均优于V2X定位方法。但在实际定位场景中，复杂的车路环境、辅助节点坐标误差、恶劣天气等多方面因素都会对定位精度产生一定的影响。因此，在后续工作中还需对各影响因素进行深层次的探究和改进，从而进一步提升定位性能。