应用加权高斯模型的非理想稀疏信道估计*
2021-04-25高童迪秦学珍袁正道王家斌
高童迪,秦学珍,袁正道,2,王家斌
(1.河南开放大学 人工智能工程研究中心,郑州450002;2.郑州大学 信息工程学院,郑州450001;3.中船重工第七一三研究所,郑州450001)
0 引 言
在现代通信系统中利用稀疏性进行信道估计时,非零信道抽头的位置和个数将对估计算法产生巨大的影响[1-2]。现有的稀疏估计算法通常假定非零抽头位置随机分布,抽头取值为零均值的高斯分布。但是在空间传播过程中,信道由直射和散射路径共同构成,非零抽头的位置和幅度具有一定的先验信息[3]。
常用的稀疏估计模型有稀疏贝叶斯学习[1](Sparse Bayesian Learning,SBL)、伯努利-高斯[4](Bernoulli-Gaussian,BG)模型和正交匹配追踪[5](Orthogonal Matching Pursuit,OMP)等,其中SBL模型假设抽头元素为均值为0、方差为伽玛分布高斯变量;BG模型假定抽头元素有零和非零两种取值(伯努利分布),其中非零元素又服从高斯分布;OMP算法将待估计向量分解为相互正交向量的稀疏线性组合,通过迭代构建稀疏逼近。基于上述三类先验模型,国内外多个团队进行了深入的研究。例如利用消息传递算法进行SBL[6]和BG[4]模型的建模和推导,也取得了较高的估计精度。但是上述工作均未考虑信道抽头所具有的分组特性,而是将每个抽头都当作独立分布。预期利用上述分组特性将成为稀疏估计算法的突破点。
最优估计通常要求解系统中所有显性和隐藏变量的全局最大后验概率,但是现代通信系统涉及到的中间变量过多,针对这样的复杂模型,最优估计会导致极高的复杂度,很难得到推广。作为最优估计的近似,因子图-消息传递算法[7]自从提出以来在稀疏估计[6]、迭代接收机设计[8]和图像处理[9]等领域得到了广泛的应用。目前应用最广泛的基本消息更新规则有置信传播[10](Belief Propagation,BP)、平均场[11](Mean Field,MF)等,在此基础上发展出了一系列近似消息传递算法,如广义近似消息传递[12](Generalize Approximate Message Passing,GAMP)和酉近似消息传递[13](Unitary Transform Approximate Message Passing,UT-AMP)等。上述每种规则都有特定的应用场景,如BP规则合适用于离散分布的变量计算,MF规则适合如高斯分布和Gamma分布的消息计算,但是针对更为复杂的参数计算,BP和MF规则也很难得到闭式解。文献[14]中证明了经典的期望最大化(Expectation Maximization,EM)方法也可以看作MF规则的一个特例,能够作为一种消息更新规则嵌入到现有的消息传递算法中,以适用于更复杂的参数估计[15]。
针对非理想稀疏信道,本文提出了一种应用联合UT-AMP和EM的信道估计算法,并建立虚拟环境进行了测试,从数值仿真和复杂度的角度验证了所提算法的有效性。
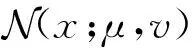
1 系统模型
1.1 OFDM系统模型
针对一个配置有M个子载波的正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统,均匀选择其中N个作为导频进行信道估计,剩余M-N个用于数据传输,导频向量可表示为x=[x1,x2,…,xN]H。定义导频图谱为P,即向量x中元素xn的下标n∈P。频域传输符号经过频域等效信道h=[h1,h2,…,hN]H的传输得到的频域接收数据为y=h·x+n。由于本文仅关注信道估计,则向量h、y等默认仅包含频域索引属于导频图谱P的部分,即h、y∈RN×1。为简化系统模型,本文假定发送的导频符号为xn=1,则观测数据y可以简化表示为
y=h+n。
(1)
式中:n表示精度(方差的倒数)为σ-1的加性高斯白噪声。根据传播理论,OFDM系统的频域等效信道可以表示为多径抽头向量α和部分离散傅里叶变换(Discrete Fourier Transform,DFT)矩阵相乘的形式,即
h=Φα。
(2)
式中:α∈RL×1为抽头向量,L为抽头长度。式(2)中矩阵Φ的构造方法为:从M维标准DFT矩阵FM中选取其索引属于导频图谱P中的N行和前L列,即Φ∈CN×L。进而式(1)可以重写为
y=Φα+n。
(3)
但是由文献[16]等可知,当观测矩阵具有病态特性时,基于消息传递的迭代算法会导致较大的性能损失,甚至产生发散。处理该类问题的方法有向量近似消息传递(Vector Approximate Message Passing,VAMP)、酉变换近似消息传递(UT-AMP)和简单的数值处理方法,如迭代阻尼[16](Damping)的方法。本文采用UT-AMP的思路,首先对部分DFT矩阵Φ进行SVD分解可得Φ=UΛV,其中U、V为酉矩阵,Λ为对角阵,从而式(3)需要重写为
y=UΛVα+n。
上式同时左乘矩阵UT可得
UTy=ΛVα+UTn≜Aα+UTn≜h′+n′≜r。
(4)
式中:A、r和h′分别为新的测量矩阵、观测向量和频域等效信道。鉴于本文后续仅用到变量h′,简洁起见由h代替。由于UT为酉矩阵,则n′仍为高斯白噪声,并且均值方差和n一样,因此本文后续仍用n表示。所以式(4)可重新整理为
r=Aα+n。
(5)
1.2 混合高斯先验模型
在稀疏估计模型中常见的伯努利-高斯先验可以表示为
式中:稀疏向量α中的元素αl只可能有0和非零两种取值,其概率分别为(1-λ)和λ,当取值非零时假定其服从均值为0、方差为1的高斯分布。
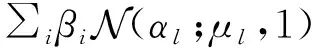
(6)
式中:βi和μl为每个高斯先验的权重和均值。相比BG模型,加权高斯模型更具通用性,能够捕捉更复杂的稀疏先验。
由上述OFDM传输和加权高斯先验模型,可以将本系统中的观测和未知变量的全局后验概率进行因式分解:
p(r,h,α,λ,π,β,μ)=
p(r|h,λ)p(h|α)p(α|π,β,μ)p(λ)=
p(σ)∑np(rn|hn,λ)p(hn|α)×
∑lp(αl|π,β,μ)p(β)p(μ)≜
fλ∑nfrnfhn∑lfαlfβfμ。
(7)
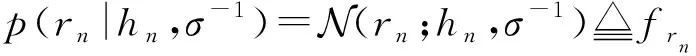
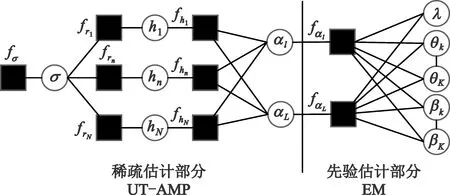
图1 因式分解(7)所对应因子图
2 消息传递框架下EM算法的嵌入
作为一种经典迭代算法,EM已经被广泛应用于信号处理的诸多领域。文献[14]中证明了EM算法可以看作是MF消息更新规则的一种特例。为了方便本文的后续推导,可以将EM算法在消息传递框架下的嵌入方式进行总结。
假设存在如图2所示因子图模型,fx(x,θ)表示变量x和θ之间的函数关系,函数fθ(θ)为变量θ的先验分布。设变量x的置信为b(x),根据MF规则可计算fx(x,θ)到θ的消息为
则变量θ的置信可写为b(θ)∝mfx→θ(θ)×fθ。
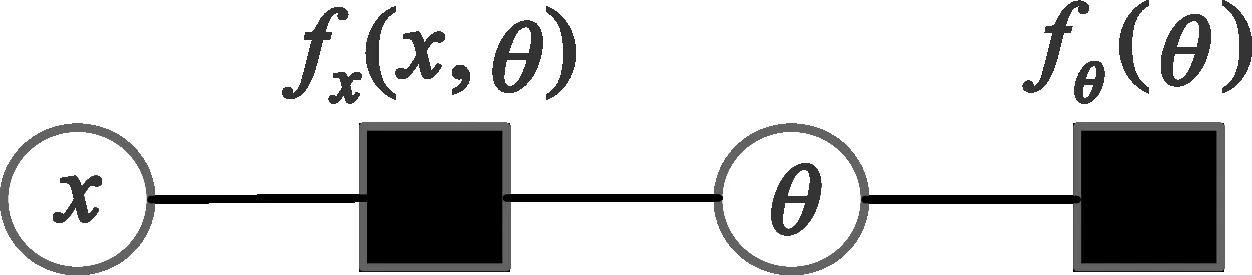
图2 EM算法简单示例因子图
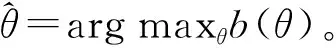
(8)
3 非理想稀疏信道估计算法推导
本节将因子图划分为稀疏向量估计部分(包含函数节点frn、fhn、fλ和与之对应的变量节点)和WG先验估计部分(包含函数节点fαl、fβ和fμ),并按照上述划分进行消息的更新和算法总结。
3.1 基于UT-AMP的稀疏向量估计算法
对于frn、fhn节点之间消息的更新可以参考文献[13]中的现有公式,但是文献[13]中并没有给出在具体先验条件下αl置信的计算,所以本节仅关注变量αl置信的更新。
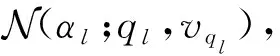
(9)
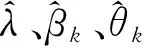
(10)
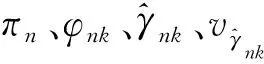
(11)
(12)
φnk≜ξnk/∑k′ξnk′,
(13)
(14)
(15)
式(12)~(13)根据简单的移项等算术运算即可得到,式(14)~(15)的计算需要利用高斯分布相乘公式。在得到置信b(αl)后计算αl的期望和方差分别为
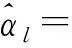

需要说明的是,本节仅推导了稀疏向量估计中置信b(αl)的更新方法,而其他节点之间消息的更新归纳在3.3节伪代码中。
3.2 基于EM的先验参数估计

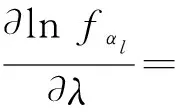
(16)
根据EM求解公式(8)有
上式代入b(αl)和∂lnfαl/∂λ可得
δ(αl≠0))∂(lnfαl)/(∂λ)dαl=
∑l(-(1-πl)/(1-λ)+πl/λ)=0,
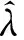
(17)
类似地,可得函数fαl对θk的偏导数
代入EM求解公式,有
(18)
(19)
3.3 本文所提信道估计算法
根据前述消息传递算法推导,设计合理的消息更新策略,本文所提信道估计算法伪代码如下:
2 酉变换[U,Λ,V]=svd(Φ),r=UTy,A=ΛV
FORi=1:NOuter
3 ∀n更新νpn=∑l|Anl|2ναl
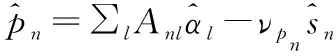
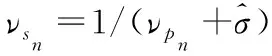

7 ∀l更新νql=(∑n|Anl|2νsn)-1
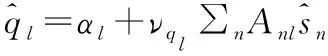
FORi′=1:NEM
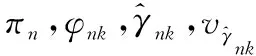
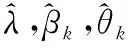
END FOR
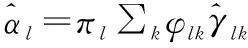
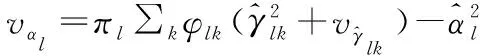
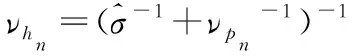
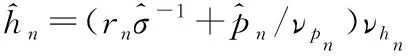
END FOR

4 数值仿真和复杂度分析
本节从数值仿真和复杂度两方面对本文所提算法和文献中方法进行对比。为方便描述,本文对涉及到的算法进行如下定义:文献[6]中所提基于SBL模型和GAMP的估计算法简写为GAMP-SBL;文献[4]中利用GAMP和BG先验的估计算法简记为UT-BG;本文所采用基于UT-AMP和WG模型的方法记为UT-WG。此外,本文还将已知非零元素位置的最小均方误差估计作为接收机性能的最佳下界,简记为Gen-LMMSE。
4.1 复杂度对比

对比算法GAMP-SBL和UT-BG在迭代部分具有复杂度O(NOuterNL),比本文所提UT-WG算法缺少了酉变换和内迭代。需要说明的是,对于方阵SVD分解并没有快速算法,但是非方阵(如“胖”矩阵或者“高”矩阵)则有快速算法,能够在N≫L或L≫N的条件下实现复杂度远小于O(N3)。矩阵A的快速SVD分解在Matlab中写为svd(A,‘eco’),仿真中能够大大加速运算。所以可以说本文所提算法与文献中已有算法相比略有提升,但保持同阶。
4.2 仿真环境建立
本节建立OFDM传输环境对本文所提算法进行数值仿真和对比。假设一个配置有M=512个子载波的单天线高速OFDM系统,均匀选取其中N=70~100个子载波作为导频。设信道抽头长度为L=200,主要非零抽头个数为S=8。由于存在多径散射,假定每个主要抽头携带3个拖尾(Heavy Tailed)非零抽头,其强度与其归属的主要非零抽头呈幂次递减。例如当抽头αl为主要的非零抽头,其强度为αl=d,则存在3个拖尾抽头,具有强度αl+j=d×2-j,j=1~3。每次仿真假定主要抽头位置随机分布,强度服从高斯分布。图3展示了上述信道的一次实现,其上半部分为受拖尾影响的抽头向量,下半部分为主要抽头向量。
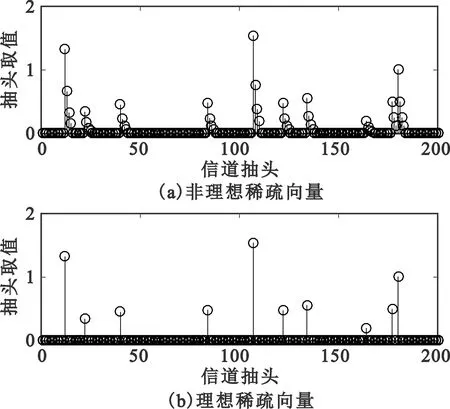
图3 非理想和理想稀疏向量
4.3 数值仿真
本节以信道抽头向量α的归一化均方误差(Normalized Mean Square Error,NMSE)为性能衡量标准对本文所提算法和文献中已有方法进行数值仿真和对比。
图4展示了在信噪比30 dB的情况下,各种算法的估计性能随导频数量的变化曲线。从图中可以看出在导频数量充足时(当N>95),所有估计算法与最优估计(Gen-LMMSE)性能接近,但是随着导频数量的降低,各类算法性能恶化严重,在N≤80时甚至几乎不工作;在导频数量处于80≤N≤95时,本文所提UT-WG算法相比GAMP-SBL和UT-BG算法有明显的性能优势,或者说在相同估计性能条件下,本文所提算法能够减少导频的使用,提升OFDM系统频谱效率。
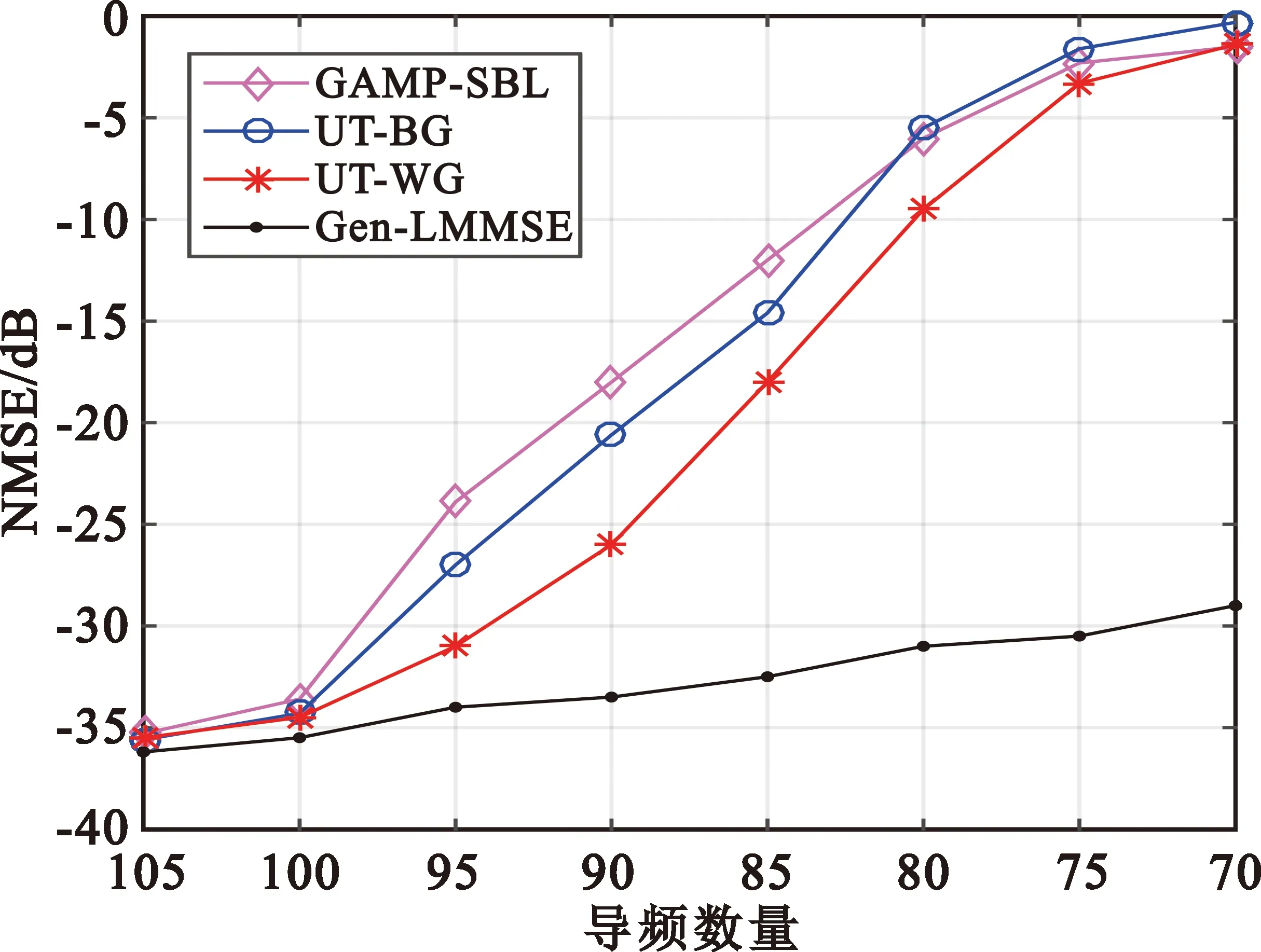
图4 估计性能随导频数量变化曲线(信噪比30 dB)
图5给出了在导频数N=85的条件下各种算法信道估计性能随信噪比的变化曲线。由于本文采用的下界是已知非零抽头位置的LMMSE估计,并且仿真中导频数量N并不充足,所以在图4和图5上各类算法估计性能相比还有一定距离。从图5中仍可以看出,相比文献中已有算法,本文所提UT-WG算法表现出3~4 dB的性能增益。
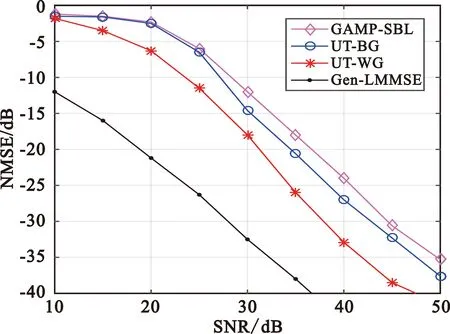
图5 估计性能随信噪比变化曲线
总之,由于采用了更合理的稀疏先验分布,利用UT-AMP算法降低了DFT矩阵的病态特性所导致的发散,本文所提UT-WG算法在保持同阶复杂度的条件下具有更优的估计性能和频谱效率。
5 结 论
本文以因子图-消息传递为建模和信号处理工具,利用加权高斯为稀疏先验模型,通过嵌入EM算法到消息传递框架中,通过消息的推导计算和迭代,得到一种针对非理想稀疏向量的估计算法,将其应用于高速OFDM通信系统信道估计的仿真中,取得了较好的性能增益。
