通信电子战系统的排队论建模及效能分析*

赵禄达，王 斌,b，姜福涛

(国防科技大学 a.电子对抗学院;b.第三学科交叉中心,合肥 230037)

0 引 言

在现代智能化战争中，通信手段日新月异，通信电子战装备也在不断发展，使得作战双方始终处于激烈争夺相互交织的电磁频谱的状态。近年来，通信电子战地位作用越来越凸显，成为战场上至关重要的一环。目前，排队论理论在军事细分领域运用十分广泛。文献[1]最早将这一理论运用到电子对抗中来。在此基础上，文献[2]对通信网络系统进行了建模研究，给出了一种通信网络效能评估方法，对通信电子战建模具有参考意义。文献[3]对雷达电子战领域进行了建模研究，提出了基本建模方法。文献[4]进一步对不同战术背景情况下的雷达对抗系统进行分析，但是没有考虑实际作战目标的威胁程度。文献[5]分析了两个不同威胁等级目标的雷达电子战模型，但没有考虑自身作战系统的工作方式。另外，目前对于电子战系统效能分析研究集中在系统整体仿真和平台搭建上[6-7]，针对具体类型的装备评估也多为雷达电子战系统效能分析，在研究电子战系统效能时也没有将多个雷达电子战系统工作状态考虑在内，且对通信电子战系统的效能评估研究较少。

为此，本文将针对战场实际，充分考虑多个电子战系统在工作方式下的具体情况，对通信电子战系统作战进行分析建模，提出一种基于排队论的通信电子战系统的效能分析思路，有利于深入分析不同战场条件下通信电子战系统的运用方法，为决策者提供建设性的参考意见。

1 通信电子战系统效能模型

1.1 问题的提出

通信电子战作战系统由串行或协同工作的n套通信电子战装备组成，每套电子战装备包含1台通信电子战侦察装备和若干台通信电子战干扰装备(服务台)，多目标干扰能力为m。其作战任务为对敌通信组网(顾客)实施侦察干扰，迟滞敌方通信，对敌指挥链路进行打击。

在实施干扰时，认为干扰区域各个子通信电子战系统共有可叠加，对在干扰区工作的敌方通信目标指定1个干扰机(通道)进行服务。如果敌方通信网络在干扰区域内正常工作时我方没有空闲的通信电子战干扰装备，而在工作结束前产生了空闲干扰站，这样也视为成功干扰1次。

对问题提出如下假设：

(1) 敌通信网络工作时间间隔符合服从于参数λ(个/min)的负指数分布的最简流(poisson流)。

(2) 敌通信组网工作时间间隔近似相等，在干扰区域内的工作时长为有限的。

(3) 每个通信电子战系统多目标干扰能力为m(即可同时干扰m个敌方正在工作的通信组网)，其干扰敌方网络时间服从参数为μ的负指数分布。

(4) 不考虑敌方的电子战反制措施且敌方通信网络抗干扰措施对我方电子战装备稳定工作没有影响。我方通信电子战侦察装备发现敌通信网络正常工作的概率为Pf。敌方通信网络在正常工作时被我方电子战系统截获，系统成功干扰目标的概率为Pk。

(5) 系统的服务规则为先到先服务(First In First Out,FIFO)，指通信电子战系统对最先侦察到的并且在正常工作的通信组网进行干扰。

1.2 通信电子战系统效能模型的构建

1.2.1 通信网络干扰分析模型

定义第i套通信电子战装备发现敌通信网络正常工作的概率为Pfi，敌方通信组网正常工作时未被我方成功干扰的概率为PTi,整个干扰流程如图1所示。

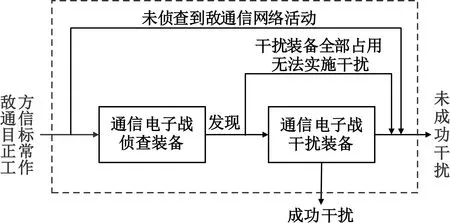
图1 通信电子战装备干扰流程示意图

敌方通信组网被第i套通信电子战装备侦察后，有可能部分组网未被侦察站发现，因而不会被列为干扰目标，最终未成功干扰；有可能被侦察站发现，成为我干扰站的干扰目标，存在以下三种情况：

(1) 我方干扰站由于多目标干扰能力的限制处于非空闲状态，不能为敌通信组网服务，其概率定义为πi。

(2) 由于敌通信组网抗干扰能力较强，我方干扰站对其干扰后仍能正常工作。

(3) 我方干扰站成功干扰敌通信组网正常工作。

由此可得到敌方通信组网未被第i套通信电子战装备成功干扰的概率PTi=未被侦察站发现的概率+被侦察站发现的概率×(干扰站处于非空闲状态的概率πi+我方干扰站对其干扰后仍能正常工作的概率)，即

PTi=(1-Pfi)+Pfi×[πi+(1-πi)·(1-Pk)] ，

(1)

化简得

PTi=1-PfiPk(1-πi) 。

(2)

由于通信电子战系统近似看成消失制的排队系统，则干扰站处于非空闲状态的概率为

(3)

1.2.2 不同工作类型下的效能模型

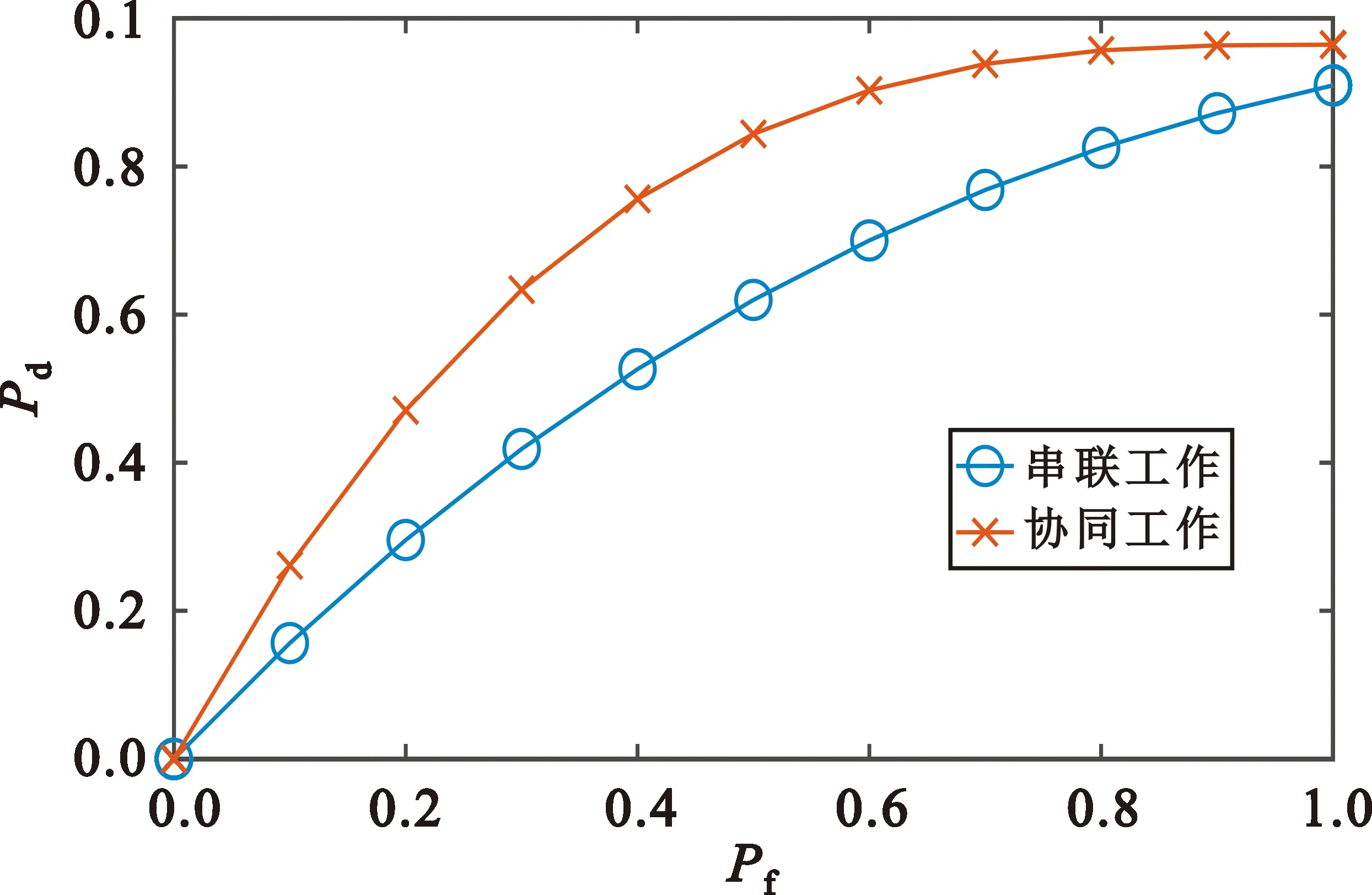
在实际运用过程中，通信电子战系统一般分为串联型运用和协同型运用两种模式。串联型工作模式指多个电子战系统串联配置，在接收到敌通信网络信号后根据每级系统的通信网络干扰能力实施接续识别和干扰。此工作类型对整体系统的工作负载较小，但干扰效率和效果欠佳。协同型工作模式指多个电子战系统并联配置，在接收到敌通信网络信号后根据通信网络性质和数量同时在每级系统进行识别和干扰。此工作类型干扰效率和效果较好，但对整体系统的工作负载较大。需要指出的是，两种类型中关于干扰成功率的计算均基于每个系统都有能力干扰敌人这个假设。这种假设是合理的，因为本文中基于排队论的系统建模建立在每个通信电子战系统均可在战技性能良好的情况下对已经判断通信网络类型的通信网络实施侦察干扰，并且在实际运用过程中，每个系统并不仅仅存在单一干扰方式，系统会根据接收到的通信网络类型灵活判断和选择干扰方式。在战役、战术行动中，指挥员会根据战场实际和任务情况部署装备位置和数量，一般由2～3套装备组成1个子系统，对敌实施侦察干扰。串联型和协同型运用示意图见图2和图3。

图2 串联型通信电子战系统

图3 协同型通信电子战系统

在串联型工作模式中，由于每一套通信电子战装备相互独立，则我方未成功干扰敌方通信组网的概率为

(4)

我方通信电子战系统干扰效能为

(5)

类似地，对于协同型通信电子战系统而言，由于信息共享机制和干扰不受限机制，每一套通信电子战装备相互独立，则其联合侦察概率和成功干扰概率为

(6)

我方未成功干扰敌方通信组网的概率为和我方通信电子战系统干扰效能分别为

(7)

(8)

最后，为便于说明数据有效性和模型优劣，定义通信电子战系统作战效费比。易知，我方通信电子战装备对敌通信网络干扰效果可理解为NPk/n，N代表敌方所有正常工作的通信组网数量，则效费比与其成正比：

η=εNPk/n。

(9)

式中：ε为调节系数。

2 通信目标分级下的系统效能改进模型

在战场实际执行上级指定的通信电子战任务时，一般会按照作战任务前确定的决心建议中对敌方通信网络重要性的高低划分进行干扰任务具体规划，对敌方通信枢纽、指挥专网等重要性分级较高的目标会实施优先干扰。这样，上文中设定的随机服务系统模型就要进行相应改进。先提出以下假设：

(1) 为便于计算和说明，本文仅研究存在2个分级的通信网络干扰问题。

(2) 敌方战场上存在两个分级的按照poisson独立流工作的通信组网，分别服从于参数为λ1、λ2(单位：个/min)，我方通信干扰装备数量为n，仍为点对点式的干扰，干扰敌方2个分级网络时间服从参数为μ的负指数分布。

(3) 第一分级的通信网络等级(优先权)高，如果在干扰第二分级的通信网络时侦察出第一分级的通信网络开机工作，则我方干扰站终止对第二分级的通信网络实施干扰转而对第一分级网络进行干扰；若所有干扰机正在对第一分级网络实施干扰的过程中第二分级的网络开机工作且被我方侦察站侦察得知，此时不会对其实施干扰，敌方此网络未成功被干扰。

(4) 通信电子战系统此刻状态为N(t)=(i,j)，系统有i个第一分级的目标，有j个第二分级的目标，2维马尔科夫过程，此时模型加强为一个M/M/n/n型随机服务模型。

根据文献[8]推导可得到系统的状态稳定方程为

(10)

方程达到稳定的条件为λ1

(11)

再代回式(4)～(9)即可得到此模型下的相关参数结果和结论。

3 算例分析

本文中的仿真分析测试环境数据如表1所示。

表1 测试环境

下文中的仿真数据取自文献[10]，改进模型数据根据实际进行合理假设。

3.1 基本模型分析

假设敌方通信组网开机正常运行时间间隔满足简单流λ=6个/min，每个通信干扰系统的侦察站侦察发现概率为Pf，干扰站成功干扰通信网络的概率为Pk，进行干扰的效率为μ=2个/min，下面定义通信电子战系统效能模型中的工作方式相关数据：

(1)串联型通信电子战系统中，共有n个相互独立的系统进行侦察干扰，每个系统内存在m台通信电子战干扰装备，其中m≥2。

(2)协同型通信电子战系统中，共有n级相互独立的系统进行侦察干扰，每个系统内存在m台通信电子战干扰装备，其中m≥2。

下面对通信电子战系统效能模型中不同工作类型的通信电子战系统进行分析。根据第1节中推导的式(5)、(8)、(9)可知，提高系统效能需要提高系统的侦察发现概率、干扰成功概率或者增加通信电子战系统个数、减小未成功干扰概率，但在多个系统级联情况下，指标变化趋势和决策建议就需要进一步进行详细的讨论。

通过式(3)和式(5)可得出串联型工作模型的系统效能，通过式(8)和式(5)可得出协同型工作模型的系统效能，以下分四种情况对两种工作方式下的模型进行分析，得出系统干扰总效能Pd与侦察站侦察发现概率Pf、系统成功干扰敌方概率Pk、每个系统干扰站数量n、系统数量m之间的关系，并比较两种工作方式的差异。仿真结果如图4所示。

(a)Pk=0.5,n=3,m=4

其中，图4(a)表示系统成功干扰敌方概率Pk为0.5、每一个系统干扰站数量为3、通信电子战系统数量为4时，系统干扰总效能Pd和侦察站侦察发现概率Pf之间的关系；图4(b)表示侦察站侦察发现概率Pf为0.8、每一个系统干扰站数量为3、通信电子战系统数量为4时，系统干扰总效能Pd和成功干扰通信网络概率Pk之间的关系；图4(c)表示成功干扰敌通信网络概率Pk为0.5、侦察站侦察发现概率Pf为0.8、通信电子战系统数量为4时，系统干扰总效能Pd和每一个系统干扰站数量n之间的关系；图4(d)表示成功干扰通信网络概率Pk为0.5、侦察站侦察发现概率Pf为0.8、每一个系统干扰站数量为3时，系统干扰总效能Pd和通信电子战系统数量m之间的关系。

由图4可以得出以下结论：

(1)无论是串联型还是协同型工作方式，提高Pf、Pk、n、m均可提高电子战系统作战效能。两种类型工作方式下的系统效能均随系统侦察概率Pf增大而增大，在系统侦察概率为0.55之前协同工作方式优于串联工作方式，之后则相反。两种类型工作方式下的系统效能均随成功干扰通信网络概率Pk增大而增大，协同工作模式下在概率小于0.7之前效能值保持较高，优于串联型工作方式，之后则串联工作方式更加优越。两种类型工作方式下的系统效能均随干扰站数量n增大而增大，协同工作模式在n=2之后对效能的贡献度低于串联工作模式，在此情况下选用串联工作模式较为适合。两种类型工作方式下的系统效能在m=4之前均随干扰站数量增大而增大，单个系统工作时选择串联工作模式较好，协同工作模式在m=2之后对效能的贡献度高于串联工作模式，在此情况下选用协同工作模式较为适合。

(2) 从图4(c)中可以得出，每个电子战系统干扰站数量的增加会提高系统效能值，但在n≥3之后，协同型工作方式提高得并不明显。为此，进一步分析此条件下的系统效费比，根据式(9)得出图5所示曲线。

图5 电子战系统效费比曲线

可以得出，随着通信电子战系统干扰站数量的增加，效费比呈现出下降趋势，图5中当n≥3之后效费比衰减程度并不明显，在实际运用中不论使用何种工作方式，都应当谨慎考虑干扰站数量，以免造成我方资源的浪费。

(3)从图4(a)和图4(b)可以看出，在其他因素一定时，当Pf、Pk较小时协同型工作方式优于串联型工作方式，当Pf、Pk较大时则相反，这与我们在实际运用中的直接结论是一致的。

3.2 改进模型分析

在改进战术条件下的系统模型中，对比未分级的模型数据，取λ1=6个/min，λ2=4.5个/min，μ=2个/min，通信电子战系统组成方式依然保持串联型和协同型两种情况。其余变量相同的条件下，对改进模型进行数据分析仿真，结果如图6所示。

(a)Pk=0.5,n=3,m=4

在曲线的变化趋势上，图6(a)变化趋势与基本模型基本一致，但协同型工作方式始终优于串联型；图6(b)与图4(b)结果相差较大，在改进后的分级模型中协同工作方式出现了成功干扰概率与系统效能成反比的现象，这是由于在目标分级的情况下，优先级较高的目标会始终占用系统的可用干扰站，而等级较低的目标可能无法被当前系统干扰，造成系统效能降低的现象；图6(c)与图4(c)结果也有区别，这是由于串联模式下的通信电子战系统在服务系统“满载”情况下干扰能力大大下降，而协同模式下的通信电子战系统在服务系统依然可以正常对敌实施干扰，性能会优于串联工作模式。

在实际运用过程中，针对敌通信网络要注意以下几点：一是战前情报是收集，对敌方网络数量、工作方式、抗干扰类型等信息及时进行掌握；二是根据已有情报和电子战系统侦察情报进行敌情判断，梳理出模型需要的相关数据；三是合理选择模型和电子战系统参数，在作战费效比最小的情况下完成作战任务并达到最优的作战效果。

4 结束语

本文通过对通信电子战系统进行模型抽象，基于随机服务系统建立了一般情况下和战术背景下考虑目标优先级的系统模型，给出了系统效能的一种评价方式。对于战术条件下的模型结果给出了演算结果，讨论了数据之间的内在联系，对实际运用模型给出了参考，为电子战指挥员提供了切实可行的决策手段。但也存在不足，比如战场环境变量没有考虑在内、是否环境因素会对模型产生一定影响等，需要进一步对其进行深入分析，结合实际数据进行模型参数补充与修正。