对NBC-128 的安全性分析
2021-04-24杨江帅陈怀凤鲍金凤康潇文
杨江帅 ,陈怀凤 ,鲍金凤 ,康潇文
(1.中国电子信息产业集团有限公司第六研究所,北京 100083;2.北京联合大学旅游学院,北京 110101;3.61428 部队,北京 100097)
0 引言
为推动我国密码算法的设计及实现技术发展,培养密码学人才,中国密码学会于2018 年启动了全国密码算法设计竞赛,共22 个分组密码算法进入第一轮评估,有10 个算法进入第二轮评估[1]。其中ublouk[2]、FESH[3]、TANGRAM[4]和SPRING[5]算法采用SPN 结构,ANT[6]、SMBA[7]和Raindrop[8]算法采用Feistel 结构,NBC[9-10]和FBC[11]算法采用广义Feistel 结构。最终,uBlock 和Ballet 获得一等奖,FESH、ANT 和TANGRAM 获得二等奖,Raindrop、NBC、FBC、SMBA 和SPRING 获得三等奖。
本文将针对NBC 算法进行安全性分析,NBC 算法由徐洪等人设计并提出,支持128/128 bit、128/256 bit、256/256 bit 3 种分组和密钥尺寸。该算法的非线性F 函数部分采用16 bit S 盒,由16 级非线性反馈移位寄存器迭代而成,具有较低的硬件实现成本。差分分析[12]、线性分析[13]、不可能差分分析[14]、零相关线性分析[15-17]和积分分析[18]等是分析分组密码算法安全性的主要方法,算法设计者针对NBC 算法的各个版本给出了初步分析结果。
针对NBC-128 算法的两个版本,设计者的研究表明[9-10]:NBC-128 算法不存在9 轮有效的线性特征和差分特征。对于不可能差分攻击和零相关线性攻击,设计者在第二轮的提交文档[9]中给出了10 轮的区分器及详细的攻击过程,后来在新版本中[10]将两类路线各扩展一轮,并相应地将可攻击轮数扩展了一轮。利用不可能差分分析方法,设计者攻击19 轮NBC-128/256、17 轮NBC-128/128,利用零相关线性分析方法,可以攻击16轮NBC-128/256、15 轮NBC-128/128。对于积分分析方法,设计者给出了12 轮的积分路线,数据复杂度为2127,可以攻击18 轮NBC-128/256、16 轮NBC-128/128。
本文将针对NBC-128/256 和NBC-128/128 两个版本进行独立的安全分析,主要从不可能差分分析、零相关分析和积分分析3 种分析方法出发开展研究,相关的攻击结果比较见表1。主要贡献如下:
(1)给出NBC-128 算法的两类11 轮不可能差分路线,利用其中一类不可能差分路线进行了NBC-128/256和NBC-128/128 算法的不可能差分攻击。本文认为文献[9]中的密钥猜测过程少猜了几个子密钥,达到预期攻击轮数的计算复杂度将超过穷搜密钥复杂度。表1 给出了修正后的数据和计算复杂度估计。
(2)给出NBC-128 算法的两类11 轮零相关线性路线,基于其中一类零相关线性路线构造多维零相关区分器,在卡方统计法多维零相关攻击模型下进行了NBC-128/256 和NBC-128/128 算法的密钥恢复攻击,对于NBC-128/256 算法可以攻击到19 轮,对于NBC-128/128 算法可以攻击到16 轮,比已知的多维零相关攻击分别扩展了3 轮和1 轮。
(3)给出了NBC-128 算法基于分离特性的新型12轮积分路线,并进行了积分攻击,需要的数据复杂度仅为2125,优于原有积分攻击的数据复杂度。
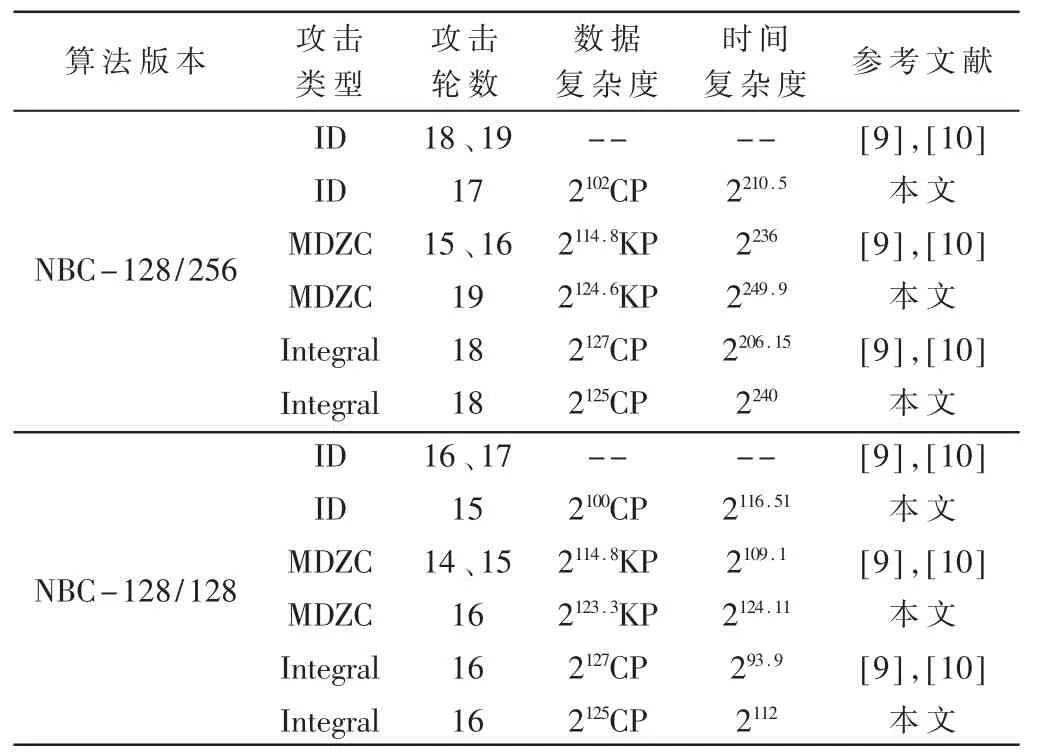
表1 对NBC-128 的攻击结果比较
1 NBC-128 算法描述

图1 NBC-128 的轮函数
NBC-128 算法采用8 分支广义Feistel 结构,迭代32轮。每个分支16 bit,每轮存在4 个F 函数,F 函数的输入为输入分支与轮密钥的异或值,经过1 个16 bit 的S 盒查表,输出与另外一个分支异或,最后经过一个分支位置变换操作。在NBC-128 算法的最后一轮,F 函数的输出与相邻分支异或后,不再进行分支位置变换操作。设第i 轮的输入为,输出为第i 轮的子密钥为其一轮变换的结构如图1 所示。
NBC-128 算法存在256 bit 和128 bit 两个密钥尺寸,本文的主要研究与密钥扩展算法关联不大,此处不再给出NBC-128 算法的密钥扩展算法。
2 对NBC-128 算法的不可能差分分析
2.1 NBC-128 算法的11 轮不可能差分路线
本节给出NBC-128 算法的两类新型11 轮不可能差分路线,其中第一类不可能差分路线在文献[10]中已被提出。
命题1:(NBC-128 的第一类11 轮不可能差分路线)
(0,Δ,0,0,0,0,0,0)/→(0,0,0,Δ,0,Γ,0,0)是NBC-128 算法的一条11 轮不可能差分路线,最后一轮不包括位置置换,其中Δ,Γ≠0,Δ≠Γ,图2 给出了该不可能差分路线的矛盾产生过程,图中* 表示差分非零,?表示差分不确定,空白位置表示差分为0。
命题2:(NBC-128 的第二类11 轮不可能差分路线)

图2 NBC-128 的第一类11 轮不可能差分路线
(0,Δ,0,0,0,0,0,0)/→(0,0,0,Δ,0,Γ,0,0)是NBC-128 算法的一条11 轮不可能差分路线,最后一轮不包括位置置换,其中Δ,Γ≠0,且Δ 与Γ 相互独立,图3 给出了该不可能差分路线的矛盾产生过程,图中* 表示差分非零,?表示差分不确定,空白位置表示差分为0。

图3 NBC-128 的第二类11 轮不可能差分路线
实际上,NBC-128 算法为每一轮具有4个F 函数的广义Feistel 结构,通过移动输入差分、输出差分中非零差分的位置,可以构造一系列类似的11 轮不可能差分路线,从结构以及攻击能力方面考虑与上述路线等价,此处不再给出具体细节。
2.2 对NBC-128/256 算法的不可能差分攻击
在文献[9]、[10]中的不可能差分分析过程中,认为作者漏猜了几个子密钥,因此实际攻击效果达不到预期的那么好。利用第一类11 轮不可能差分路线,本文对NBC-128/256 算法进行修正的不可能差分攻击,图4 给出了攻击过程中的差分及符号,主要攻击过程如下:
(1)构造Structure:Sc={X=(X0,X1,X2,X3,X4,X5,X6,X7)|(X0,X4,X5)}=c,其他位置遍历},则每个Structure 中有280个元素,可以构造约2159组符合(0,*,*,*,0,0,Δ,*)的差分对(Δ 取遍非零可能值)。
(2)通过构造m 个Structure,可以构造2t=2159×m×2-48个明文差分符合(0,*,*,*,0,0,Δ,*),相应的密文差分符合(0,*,0,0,*,*,Γ,*),Γ≠Δ,Γ≠0 的正确数据对。
(3)按照表2 进行密钥猜测及错误对筛除,对于每一个错误密钥,每一个正确对被留下的概率为2-16×8=2-128。对于错误密钥,没有差分对留下的概率为p=(1-2-128)2t≈2-114×(t-128),即剩余约2256×p 个候选正确密钥。

图4 NBC-128/256 的17 轮不可能差分攻击
(4)利用两个明文对进行候选正确密钥的穷搜,完成密钥恢复攻击。
复杂度估计:选取m=222个Structure,共需要2102个选择明文。此时,步骤(3)的总计算复杂度约为2t+80=2159+22-48+80=2213次简单计算,步骤(4)的穷搜复杂度为2256×p≈2209.82次17 轮加密。总时间复杂度约为2210.5次17 轮加密。
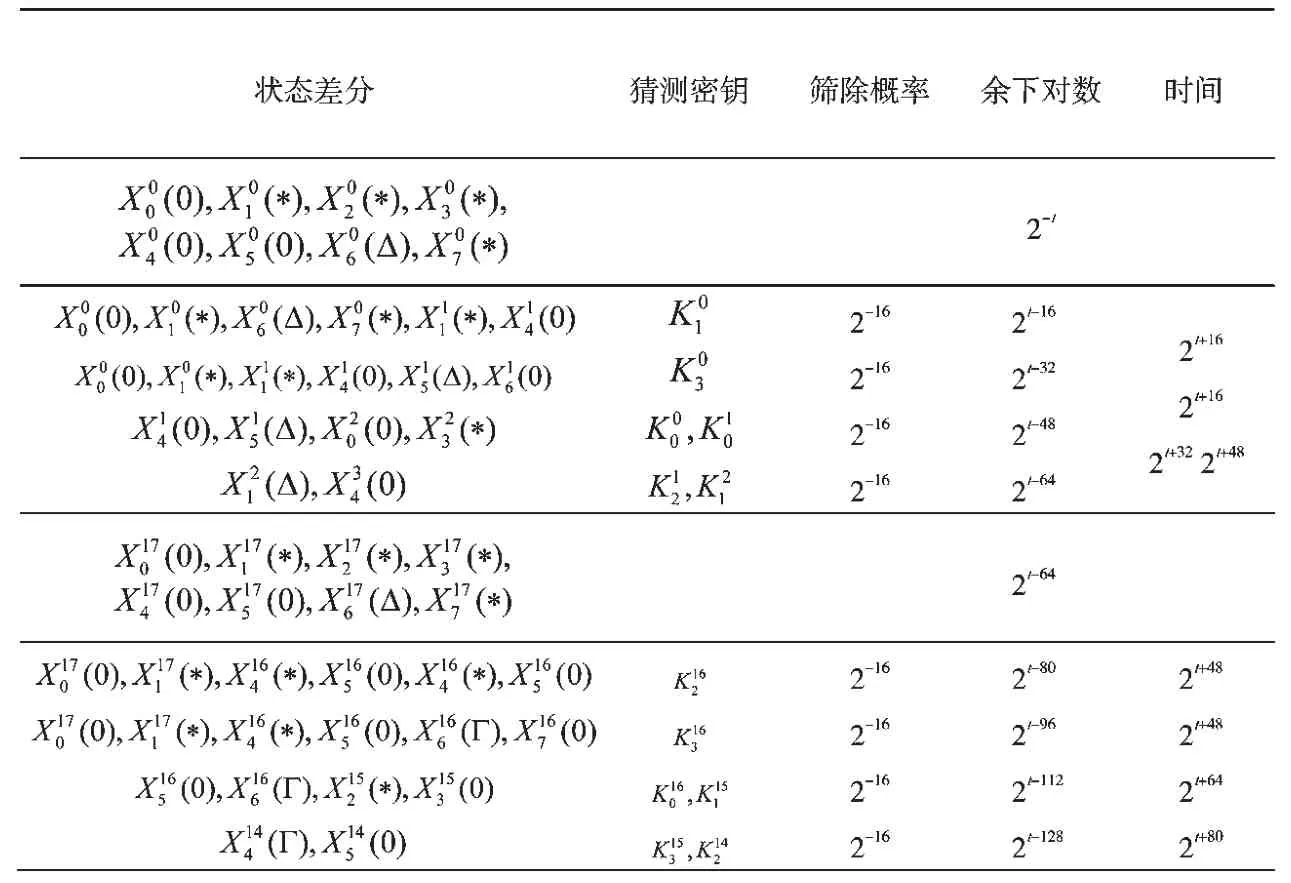
表2 对NBC-128/256 的不可能差分攻击
2.3 对NBC-128/128 算法的不可能差分攻击
对于NBC-128/128 算法,主密钥长度仅有128 bit,只能在区分器前后各添加两轮进行15 轮密钥恢复攻击。
通过选择252个Sc={X=(X0,X1,X2,X3,X4,X5,X6,X7)|(X2,X3,X4,X6,X7)}=c,其他位置遍历}类型的结构体,可以构造252+95-80=267个输入差分符合(*,*,0,0,0,Δ,0,0)、输出差分符合(0,*,0,0,*,0,Γ,0)、Γ ≠Δ 的数据对,用类似于上述的密钥猜测及错误对筛除,对于错误密钥,无差分对剩余的概率为p=(1-2-64)267≈2-11.52。错误对筛除的总计算量约为267+48=2115次简单计算,剩余约2128×2-11.52=2116.48,总时间复杂度约为2116.51次15 轮加密。需要的数据量为252+48=2100个选择明文。
3 对NBC-128 算法零相关线性分析
3.1 NBC-128 算法的11 轮零相关线性路线
本节给出NBC-128 算法的两类新型11 轮零相关线性路线,其中第一类零相关线性路线在文献[10]中已被提出。
命题3:(NBC-128 的第一类11 轮零相关线性路线)
(α,0,0,0,0,0,0,0)→(0,0,0,0,β,0,0,0)是NBC-128 算法的一条11 轮零相关路线,最后一轮不包括位置置换,其中α,β≠0,α≠β,图5 给出了该零相关线性路线的矛盾产生过程,*表示掩码非零,?表示掩码不确定,空白位置表示掩码为0。

图5 NBC-128 的第一类11 轮零相关路线
命题4:(NBC-128 的第二类11 轮零相关线性路线)
(α,0,0,0,0,0,0,0)→(0,0,0,0,α,0,β,0)是NBC-128 算法的一条11 轮零相关线性路线,最后一轮不包括位置置换,其中α,β≠0,且α 与β 相互独立,图6 给出了该零相关线性路线的矛盾产生过程,*表示掩码非零,?表示掩码不确定,空白位置表示掩码为0。
3.2 对NBC-128/256 的多维零相关线性攻击
通过选取特定形式的输入掩码和输出掩码,可以构造t=12 维的多维零相关线性区分器,例如选取α=04||06||*6,β=04||*6||06的零相关路线。在该区分器前后各添加4 轮进行19 轮算法的密钥恢复攻击,相关状态及猜测的密钥情况如图7 所示,具体攻击过程如下:
(1)对于N 个已知明文及其相应的密文数据,猜测128 bit 密钥可以计算得到,根据区分器的输入、输出掩码表示,共需存储t bit 即可,因此可将中间状态存储于296+t个计数器中。该步骤需要的计算复杂度约为N×2128次8 个S 盒的查表。(2)猜测,计算得到,可存储于280+t个计数器中。该步骤需要的计算复杂度约为296+t×2128+16=2240+t次1 个S 盒的查表。

图6 NBC-128 的第二类11 轮零相关路线
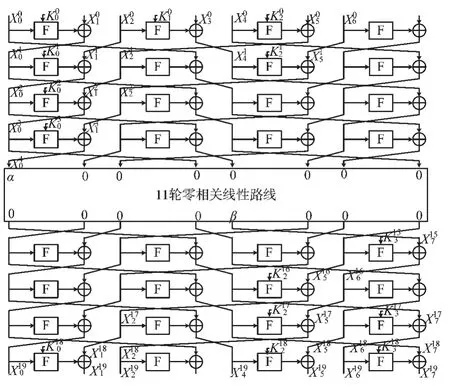
图7 NBC-128/256 的19 轮零相关攻击
(4)最终得到t 维的计数器向量,计算统计数并保留小于阈值τ 的密钥,剩余约2256×α1个候选密钥,这里α1表示将错误密钥判定为正确密钥的概率。通过至多两个明密文数据进行穷搜攻击,恢复各轮密钥。
复杂度估计[19-20]:通过设置两类错误概率α0=2-2.7,α1=2-11,这里α0表示将正确密钥判定为错误密钥的概率,可以计算出需要的不同已知明文数据复杂度为N ≈2124.5537,区分密钥使用的阈值为τ=3803.173。步骤(1)需要的计算复杂度约为T1=N×2128×(8/(4×19))≈2249.3058;步骤(2)和步骤(3)需要的计算复杂度约为T2=2240+t×6×(1/(4×19))≈2248.337;步骤(4)需要的计算复杂度约为T3=2245。综上,总计算复杂度约为2249.9487次19 轮加密。
3.3 对NBC-128/128 的多维零相关线性攻击
利用类似的t=8 维的多维零相关路线,可以在前后分别添加2 和3 轮,针对NBC-128/128 算法进行16 轮的攻击。沿用图7 的表示,进行第3~18轮的攻击,攻击过程如下:
(1)对于N 个不同的已知明文及其密文数据,可压缩为存储个数的计数器。对于,根据区分器的输入、输出掩码表示,共需存储t bit 即可,因此可将中间状态存储于296+t个计数器中。
(4)最终得到t 维的计数器向量,计算统计数并保留小于阈值τ 的密钥,剩余约2128×α1个候选密钥。通过至多两个明密文数据进行穷搜攻击,恢复各轮密钥。
复杂度估计[9-10]:通过设置两类错误概率α0=2-2.7,α1=2-8,可以计算出需要的不同已知明文数据复杂度为N≈2123.3548,区分密钥使用的阈值为τ=15905.54。步骤(1)需要的计算复杂度约为T1=N 次状态压缩;步骤(2)和步骤(3)需要的计算复杂度约为T2=2112+t×6×(1/(4×16))≈2122.585;步骤(4)需要的计算复杂度约为T3=2120。综上,总计算复杂度不超过为2124.1069次16 轮加密。

表3 NBC-128 的积分路线
4 NBC-128 算法的积分攻击
4.1 NBC-128 算法的积分路线
利用Todo 的分离特性[21]搜索方法,实现了广义Feistel结构的搜索算法,并对NBC-128 进行了积分路线搜索。搜索得到的NBC-128 算法最长积分路线为12 轮,需要的数据复杂度为2125,基于分离特性的积分路线如表3所示(文献[9]、[10]中给出的数据量为2127)。
第4 条分离特性路线的积分特性见命题5。
命题5:(NBC-128 的一条积分路线)
(A16,A16,A16,A16,A16,A16,A13,A16)→(U,U,U,U,U,U,U,B)是NBC-128 算法的一条12 轮积分路线,最后一轮包括位置置换,其中An表示n 个比特遍历,16-n 个比特取常数,U 表示异或和状态不确定,B 表示异或和为0,对应着存在积分特性的分支。
4.2 对NBC-128/256、NBC-128/128 算法的积分攻击
对NBC-128 的攻击过程与文献[9]中的描述大部分相同,下面不详细描述具体细节,只说明攻击中的不同点。
(1)本文采用的积分路线需要的数据量为2125,而不是2127。
(2)在使用2125数据量的积分区分器下,只有一个分支存在积分特性,该分支状态异或和为16 bit 全0 时对应的密钥为候选正确密钥,剩余密钥量为总密钥量的2-16。
(3)对于NBC-128/256,利用12 轮积分路线可以攻击18 轮算法,计算一个分支异或和的计算复杂度约为2204.15。因此,使用一条积分路线攻击时,总计算复杂度为2204.15+2256-16≈2240。
(4)对于NBC-128/128,利用12 轮积分路线可以攻击16 轮算法,计算一个分支异或和的计算复杂度约为292.32。因此,使用一条积分路线攻击时,总计算复杂度为292.32+2128-16≈2112。
5 结论
本文针对NBC-128 的两个密钥尺寸版本的算法,给出改进的不可能差分分析、多维零相关线性分析和积分分析结果。其中不可能差分攻击对之前的攻击进行了修正,零相关线性分析在攻击轮数上有所扩展,积分分析则降低了攻击的数据复杂度。针对NBC-128/256 的19 轮多维零相关线性攻击从轮数上来说是已知的最优攻击。
