轻量化STC-钢组合桥面板静力性能研究

李传习，雷智杰，冯峥，何伟伟，谭理

轻量化STC-钢组合桥面板静力性能研究

李传习1, 2，雷智杰1, 2，冯峥1, 2，何伟伟1，谭理2

(1. 长沙理工大学 桥梁工程安全控制教育部重点实验室，湖南 长沙 410004；2. 长沙理工大学 桥梁与建筑绿色建造和维护湖南省重点实验室，湖南 长沙 410004)

为提高密配筋STC−钢组合桥面板的经济性及施工的便捷性，研究了STC层钢筋间距对STC−钢组合桥面板弯拉静力性能的影响，提出轻量化STC−钢组合桥面板。以佛山某大桥为工程背景，设计制作了一片含两段不同配筋率的STC−钢组合桥面板条带模型。通过静力破坏试验，研究了组合桥面结构在负弯矩作用下STC铺装层的受力性能。研究结果表明：钢筋直径为10 mm，间距为80 mm的轻量化STC−钢组合桥面板，STC层的名义弯拉开裂强度达到24.66 MPa，满足实际工程设计荷载作用下的强度要求；组合桥面STC层的名义弯拉强度随着截面配筋率增大而提高，当截面配筋率提高1倍时，弯拉开裂强度可提高47.11%～50.61%；根据荷载−挠度曲线，轻量化STC−钢组合桥面板的受力过程可分为线弹性阶段、裂纹发展阶段、屈服阶段和破坏阶段；不同配筋率的STC层对正交异性钢桥面板刚度补强效果一致，在达到极限承载力之前，组合桥面板中两侧刚度相差不大，在满足实际工程需求的同时适当增大STC层钢筋间距，可方便施工、降低造价成本。

正交异性钢桥面结构；配筋率；超高韧性混凝土；弯拉开裂强度；静力破坏试验

正交异性钢桥面结构与传统混凝土桥面结构相比，具有自重轻、承载能力强、施工速度快、经济性好等优点，被广泛应用于各类中、大跨径桥梁中。大多数钢桥面采用柔性铺装，无法提供足够的刚度。在钢桥服役过程中，随着交通量的增加和车辆荷载反复作用下，正交异性钢桥面结构容易发生钢桥面铺装层破损和复杂应力状态下易疲劳开 裂[1−3]的问题。为解决这两大难题，刘梦麟[4−6]等人提出了正交异性钢板−超薄组合桥面板结构，即在正交异性钢桥面板上，通过剪力钉连接配置密集钢筋的活性粉末混凝土(reactive powder concrete, 简称为RPC)板，形成受力协同的组合桥面板，并成功应用于实际工程。张哲[7]通过钢−配筋超高性能混凝土(ultra high performance concrete, 简称为UHPC)组合桥面结构，开展纵向足尺节段模型试验和横向受弯试验，发现该新型组合桥面系弯拉开裂应力比实际工程设计荷载下的拉应力大得多，UHPC抗弯拉强度随截面配筋率和截面高度增大而提高，可通过提高截面有效高度或截面配筋率，降低组合桥面结构的开裂风险。田启贤[8]等人以军山长江大桥为工程背景，对UHPC−钢正交异性板组合桥面系进行了静承载性能试验研究。试验结果表明：组合桥面系UHPC层能满足设计荷载作用下的抗裂性能要求，并且组合桥面系的静承载能力有较大富余。Yuan[9]等人基于有限元模型，分析了UHPC作为铺装层的正交异性钢桥面板的敏感疲劳部位的应力分布。研究表明：在正交异性钢桥面上铺设UHPC，延长正交异性桥面板易疲劳区域的使用寿命，使用寿命可超过100 a；当UHPC的弹性模量降低50%时，疲劳寿命将显著降低。贺耀北[10]等人提出双边工字钢−UHPC桥面板组合梁，通过有限元数值计算和UHPC桥面板模型弯曲静力试验，分析组合梁的受力性能，揭示了UHPC桥面板的抗弯承载力和抗裂能力两者均满足实际工程要求。

超高韧性混凝土(super toughness concrete，简称为STC)因UHPC配筋后，弯拉开裂强度大幅度提高，具有更优异的韧性[11]。早期RPC应用到钢桥面铺装需要密配筋，或许是因其抗拉强度有限，所配钢筋级别较低(HRB335)[4]。随着国内外学者对UHPC的深入研究，对UHPC配合比不断进行优 化[12−14]，现阶段UHPC抗拉强度基本可维持在7 MPa以上。作者课题组采用3.5%钢纤维掺量的UHPC，抗拉强度可达到10 MPa以上，且铺装层的配筋级别较高(HRB400)，可考虑适当降低STC−钢桥面铺装层的配筋率。鉴于STC应用到正交异性钢桥面铺装层的配筋率和纤掺比还未形成统一规定，作者拟提出了轻量化STC−钢组合桥面，并以佛山某大桥STC−钢正交异性组合桥面结构为工程背景，设计并制作了一半为密配钢筋(钢筋间距40 mm)，一半为疏配钢筋(钢筋间距80 mm)的STC−钢组合桥面板条带模型。通过STC−钢组合桥面板条带模型的四点弯曲破坏试验，研究不同配筋率下组合桥面STC铺装层抗负弯的受力性能，获得条带模型的荷载−挠度曲线、荷载−应变曲线、开裂弯矩和极限弯矩等。通过ABAQUS线弹性分析和平截面假定换算截面法，计算获得STC铺装层的名义开裂强度，为轻量化STC−钢组合桥面板的工程应用提供借鉴。

1 组合桥面板条带模型静载试验

1.1 足尺模型设计

以佛山某大桥STC−钢正交异性组合桥面结构为工程背景，设计制作了一片含2种配筋率的STC−正交异性钢组合桥面板试件，如图1所示。组合试件长3 m，STC铺装层厚度为50 mm，顶部钢板厚16 mm，U肋厚8 mm，横隔板高676 mm、厚12 mm。在横隔板底部的中心处，焊一块宽112 mm的钢板用于试验梁支撑。为研究钢筋网间距对铺装层弯拉静力性能的影响，在STC铺装层中左侧(试件长度一半处)布设Φ10@80 mm×80 mm纵下横上(即纵向钢筋布置在下层，横向钢筋布置在上层)的钢筋网；右侧(试件长度一半处)，布设Φ10@40 mm×40 mm纵下横上的钢筋网，横向钢筋净保护层厚度设置为10 mm，钢筋网布置如图2所示。其中，钢筋和钢桥面板分别采用HRB400和Q345qC级钢材，疏筋段和密筋段试件的长度为1 500 mm，宽度为600 mm，净跨为450 mm，栓钉直径为13 mm、4列。但疏筋段、密筋段的钢筋间距分别为80 mm×80 mm、40 mm×40 mm。

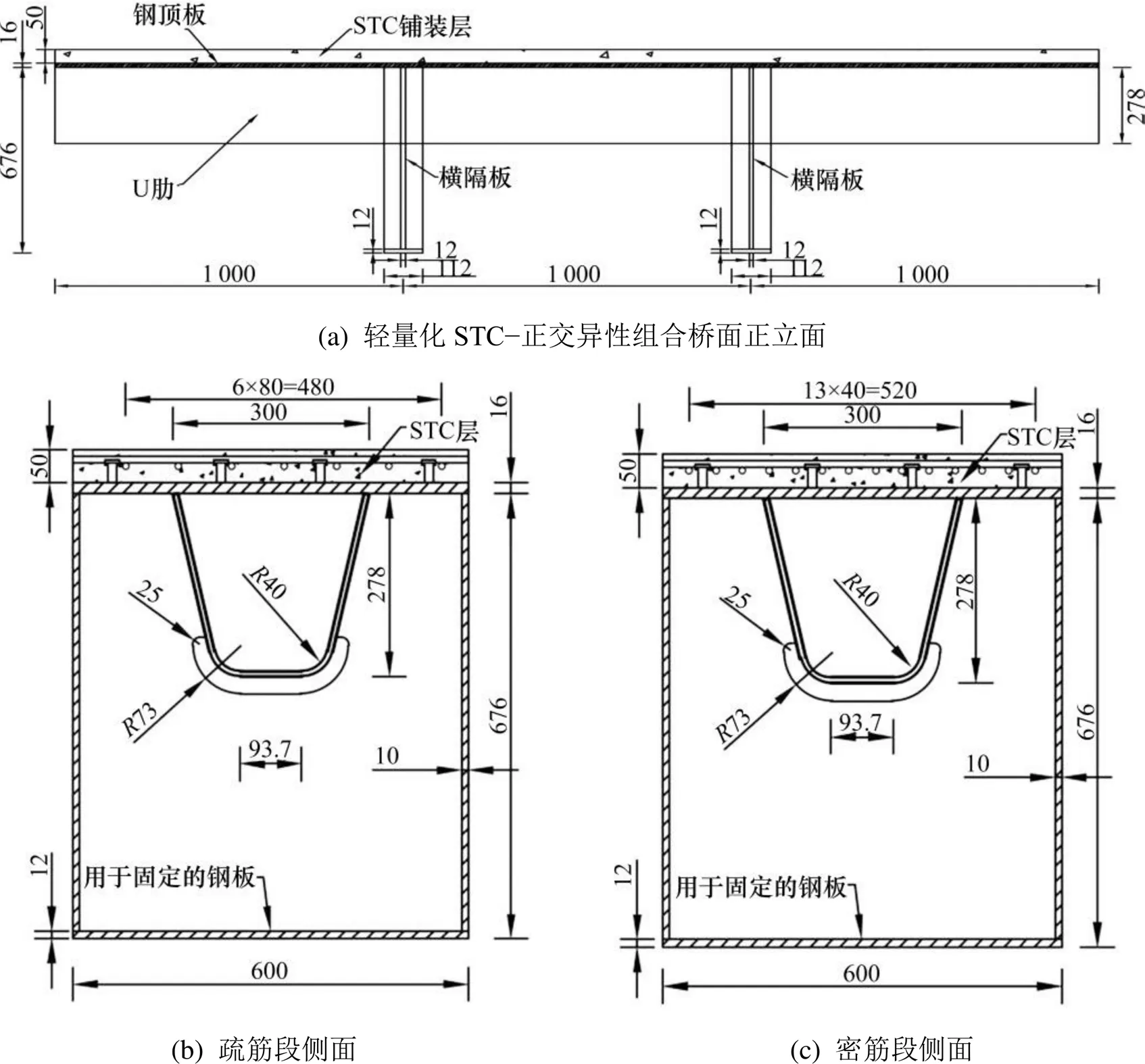
图1 试验模型示意(单位：mm)

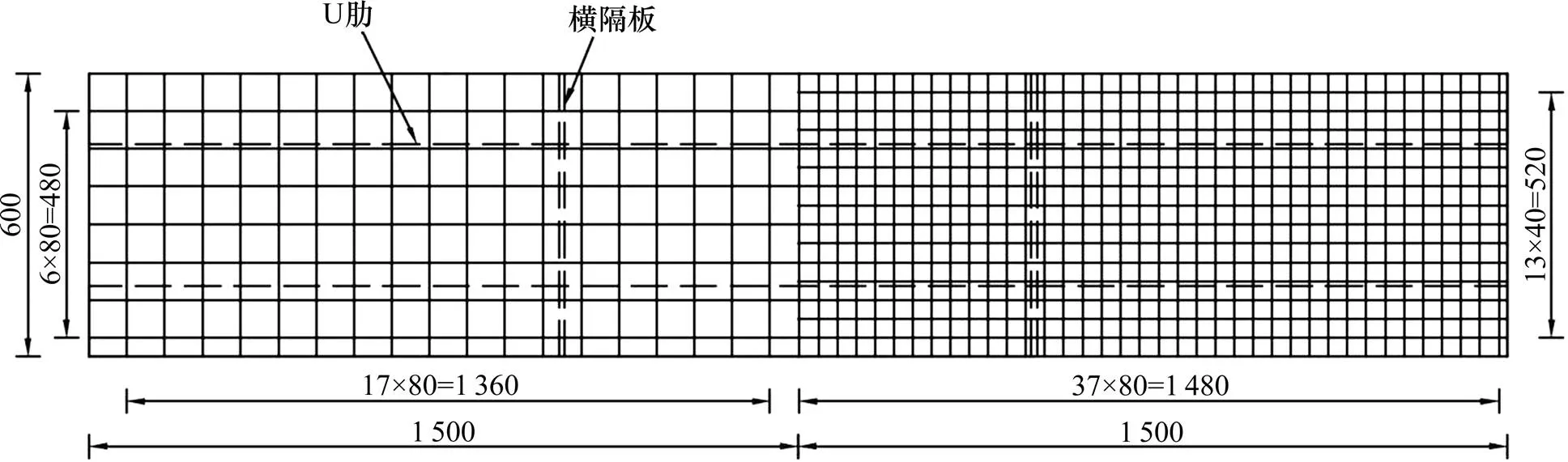
图2 钢筋布置平面图(单位：mm)

1.2 试件制作与UHPC材料特性

UHPC材料采用长沙理工大学自主研发的配合料，其主要成分为水泥、石英砂、硅灰、高效减水剂和镀铜钢纤维等。其中，钢纤维均采用端钩型镀铜钢纤维，体积掺量为3.5%，长度和直径分别为16 mm和0.22 mm。钢桥面周边架设木模板后，浇筑50 mm厚的STC层，并采用同一批搅拌料浇筑材料特性试件(3个立方体抗压试件，3个棱柱体轴压试件，3个棱柱体弹模试件，3个棱柱体抗折试件和6个狗骨头状轴拉试件)。浇筑完成后，对所有试件常温下养护48 h，拆除模板，继续进行90 ℃以上的高温蒸汽养护48 h。

养护完成后，试件的STC层表面没有出现任何收缩裂缝。通过材料特性试验，测得UHPC的立方体抗压强度为162.2 MPa，棱柱体轴心抗压强度为123.6 MPa，轴拉强度为10.2 MPa，抗折强度为42.2 MPa，弹性模量为45.04 GPa。

1.3 STC层测点布置

试验加载过程中，主要测得组合桥面板在承受负弯矩作用下STC层的拉应变，测点布置如图3所示。其中，H1～H3和H4～H6分别测量疏筋段和密筋段横隔板加载点正下方STC层的拉应变，U1～U7、U8～U10和U11～U17处应变片分别测量纯弯区STC疏筋段、跨中和密筋段的拉应变。组合桥面板底部位移计分别对称布置在疏筋段加载点、跨中和密筋段加载点三处，可测得组合桥面结构在密筋截面、跨中截面和疏筋截面的挠度。在支座处分别设置2个位移计，消除支座截面刚体位移和转角对组合桥面板挠度测量的影响。

1.4 试验加载方案

试验采用负弯矩四点弯曲加载，使用液压千斤顶，并通过分配梁传力，试验加载装置如图4所示。

加载分2个阶段进行：第一阶段采用荷载控制，荷载增量为40 kN一级，当组合桥面STC层发生初裂后，将荷载级调为20 kN一级，直至最大荷载；第二阶段改用位移控制，位移增量需根据试验时的具体情况进行调整，直至裂缝发展到一定的宽度。试验开始之前，先对试验梁采用40 kN的力，预压2次，消除松动和接触不良的影响，检查试验仪器是否正常运行。加载过程中，各级荷载作用持载3 min，消除突然加荷载的影响。每级持载结束后，均需测量各测点部位的挠度，纯弯段STC层的纵向拉应变，仔细观察试件变形及STC层裂缝发展情况。裂缝宽度采用智能裂缝宽度观测仪进行观测，荷载由精密压力传感器进行实时监控。

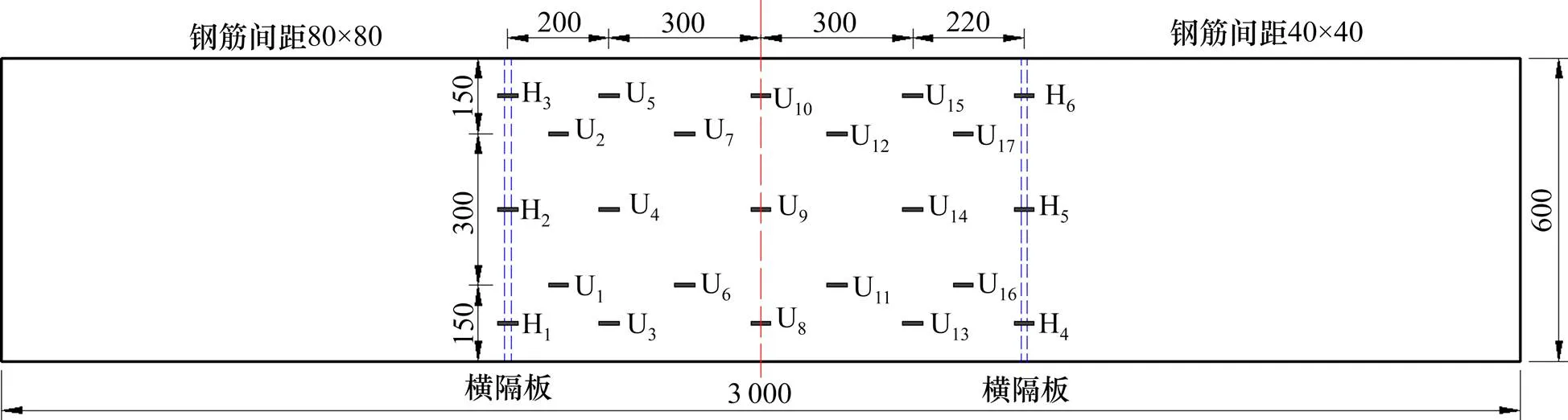
图3 STC层顶面应变片测点布置(单位：mm)

图4 组合桥面加载装置

2 试验结果与分析

2.1 STC层裂纹扩展及破坏过程

当荷载加至560.8 kN时，疏筋段STC层顶面出现第一条可视裂缝(沿横向分布)，最大裂缝宽度为0.06 mm，STC层顶面拉应变为928 με。取上一级荷载542.1 kN作为开裂荷载，即纵向受弯试验疏筋段STC层的弯拉强度，其对应STC层顶面拉应变为885 με。继续加载至695.8 kN时，疏筋段STC层顶面最大裂缝宽度扩展至0.11 mm，裂缝细而密，由疏筋段横隔板正下方向跨中逐步发展。当荷载加载达到830.3 kN时，密筋段STC层表面开始出现第一条可视横向裂纹，其宽度约为0.09 mm，取上一级荷载810.2 kN作为开裂荷载，即纵向受弯试验密筋段STC层的弯拉强度，其对应STC层顶面的拉应变为1 306 με。此时疏筋段STC层顶面的最大裂纹宽度发展至0.14 mm，其裂纹宽度发展过程如图5所示。

当荷载达到940 kN时，密筋段钢U肋底部与侧面发生屈曲现象，如图6所示。此时STC层不断出现钢纤维拔出声音。荷载增大至组合桥面达到极限承载力980 kN时，横隔板处STC层与钢顶板开始脱离，如图7所示。表明：钢−UHPC栓钉连接界面出现滑移破坏，同时STC层裂缝宽度急剧增大。

图5 疏筋段STC层表面裂缝宽度发展(单位：mm)

组合桥面结构STC层在负弯矩作用下，裂纹主要分布在加载点横隔板附近，裂纹分布如图8所示。疏筋段STC层裂纹分布密而细，密筋段STC层裂纹相比疏筋侧的少。最终因密筋段钢U肋屈曲，导致组合桥面板刚度急剧衰减而破坏。

图6 U肋屈曲现象

图7 STC层与钢顶板发生脱离

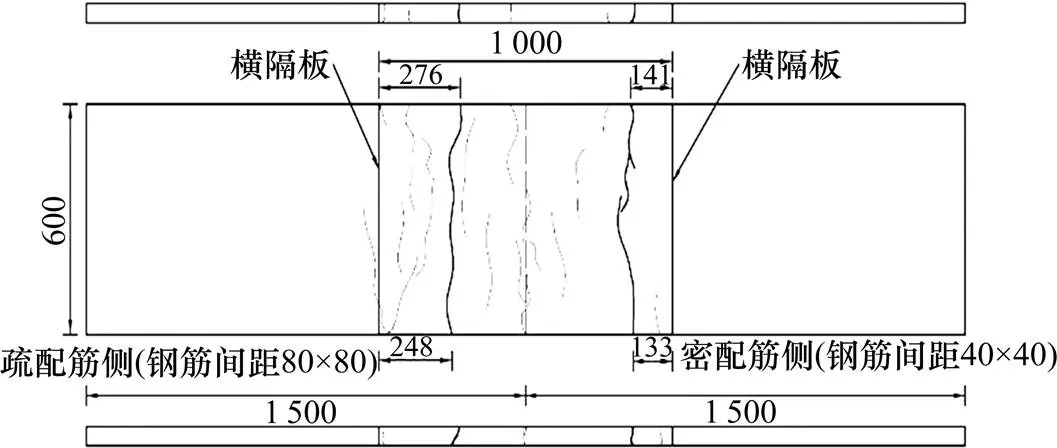
图8 STC铺装层裂纹分布情况(单位：mm)

2.2 荷载−STC层应变曲线

试验荷载−纯弯区(分疏筋段和密筋段)STC层顶面平均拉应变曲线如图9所示。为了消除裂纹贯通应变片所产生的应变测量误差，平均拉应变数据取值已剔除裂纹贯通区域的应变。

从图9中可以看出，当加载至560.8 kN时，荷 载−疏筋段纯弯区STC层的表面拉应变曲线开始变陡，应变增幅逐步增大，开始出现非线性特征。当荷载加载达到790 kN时，荷载−密筋段STC层表面拉应变曲线开始出现非线性特征。当荷载达到830.3 kN时，密筋段STC层顶面拉应变为1 395 με。当荷载增大至980 kN时，结构承载力开始呈下降趋势，组合桥面结构的承载能力达到最大。

测试表明：疏筋段STC层开裂荷载为542.1 kN，对应开裂弯矩为243.95 kN·m；密筋段STC层开裂荷载为810.2 kN，对应开裂弯矩364.59 kN·m；组合桥面板的极限承载力为980 kN，对应极限弯矩为441 kN·m。

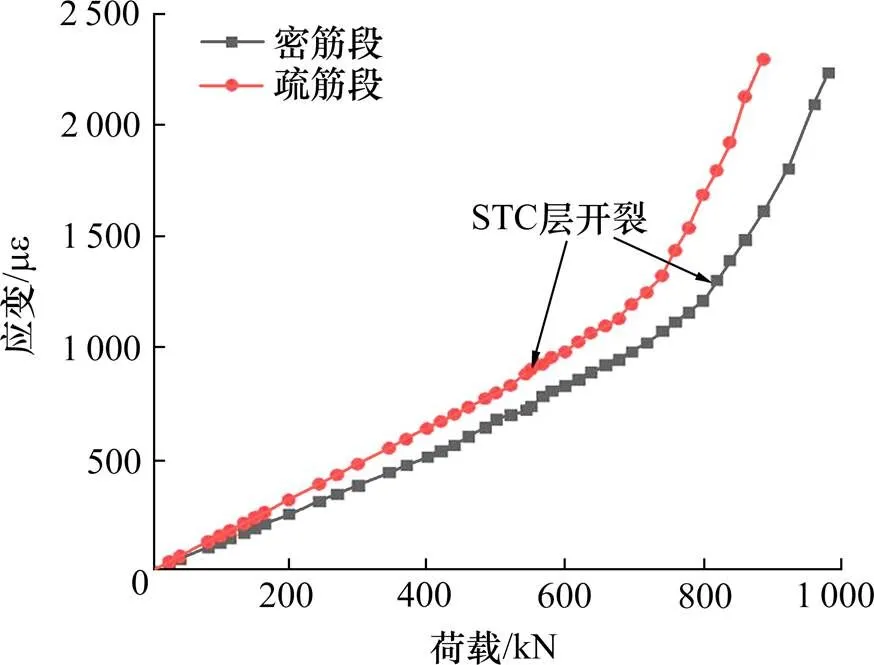
图9 荷载−平均拉应变曲线

2.3 荷载−关键截面挠度曲线

疏筋段跨中截面和密筋段STC层横隔板加载点截面的挠度随荷载变化的曲线如图10所示。实测中，挠度已扣除了支座截面刚体的位移和转角的影响。

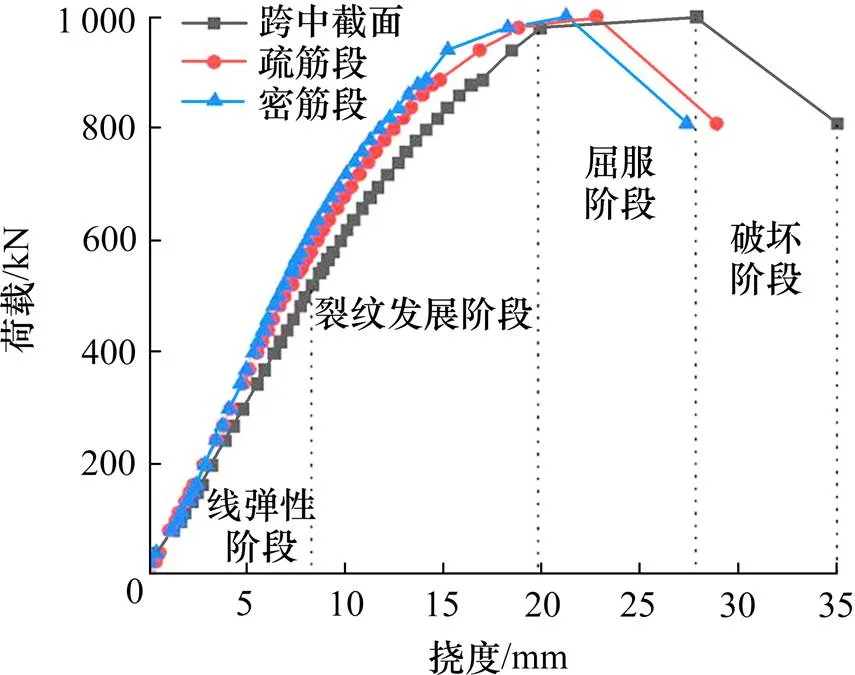
图10 荷载−挠度曲线

从图10中可以看出，STC−钢正交异性组合桥面板跨中截面荷载挠度曲线可以分4个阶段：①线弹性阶段，随着荷载增大，跨中挠度呈线性增加，组合桥面结构整体刚度保持不变，STC层未发生开裂现象；②裂纹发展阶段，跨中挠度随着荷载的增大而加速增长，组合桥面刚度开始减小，疏筋段STC层开始出现裂纹，并继续扩展；③屈服阶段，荷载增长速度减慢，挠度迅速增加，组合桥面刚度大幅降低，密筋段正交异性钢桥面U肋屈服，疏筋段STC层表面裂纹宽度增大；④破坏阶段，增大试验力，结构承载力随着挠度增大开始下降，组合桥面纯弯区横隔板加载点附近STC层与正交异性钢桥面开始脱空，组合桥面不能继续承受荷载。当荷载较小时，曲线近似呈线性，随着荷载增大，曲线逐渐趋于非线性。在达到极限承载力前，两侧不同配筋率的组合桥面板刚度一致。在屈服破坏之后，配密集钢筋一侧的刚度优势才得以表现出来。

2.4 基于线弹性名义开裂强度

采用ABAQUS有限元软件对STC−钢组合桥面板进行线弹性分析，有限元模型如图11所示。通过结合试验，可获得不同配筋率下STC桥面的名义开裂强度。

有限元模型中，STC层材料参数参考材料特性试验结果进行取值，钢材等其它材料参数按文献[15]进行取值。分配梁、正交异性钢桥面板、栓钉、STC层、支座及千斤顶均采用三维实体单元C3D8R进行模拟。钢筋采用可变形T3D2两节点线性三维桁架单元进行模拟。其中，正交异性钢桥面板与分配梁、STC−钢顶板、栓钉−钢顶板、栓钉−STC界面及STC层与支座之间的约束方式为“Tie”固结。STC层与钢筋网选取约束方式为“Embedded”约束。为保证计算精度和运算速度，将STC−钢组合桥面系的网格尺寸调小，分配梁和支座的网格尺寸适当增大，共划分单元422 883个，节点602 727个。

图11 有限元模型

经有限元计算可知，当荷载为542 kN时，疏筋段STC层的名义拉应力值(名义开裂强度)为24.66 MPa；当荷载增大到810 kN时，密筋段STC层的名义拉应力值为37.14 MPa，当截面配筋率增大1倍时，STC层开裂强度提高50.61%。

2.5 基于线弹性和平截面假定的名义开裂强度

STC−钢组合桥面系设计过程中，在负弯矩作用下，必须保持STC层的最大拉应力小于名义开裂强度。为便于实际工程的结构设计，通过组合桥面板的换算截面法，计算STC层的开裂强度，与有限元计算结果进行比较。假设钢材与STC均为理想线弹性材料，组合桥面板截面应变分布满足平截面假定，忽略钢顶板与STC层之间的滑移效应。组合桥面板换算截面如图12所示。

组合桥面板STC层换算宽度为：

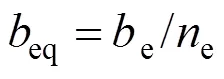
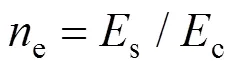
式中：e为组合桥面板的实际宽度；e为钢混凝土的弹性模量之比；s为钢板与钢筋的弹性模量，取206 GPa；c为STC层的弹性模量，取值为45.04 GPa；bs为钢筋截面应变；c为STC层的应变；eq为组合桥面换算成STC层后的有效宽度；c为STC层厚度，取50 mm；p为钢顶板厚度，取16 mm。

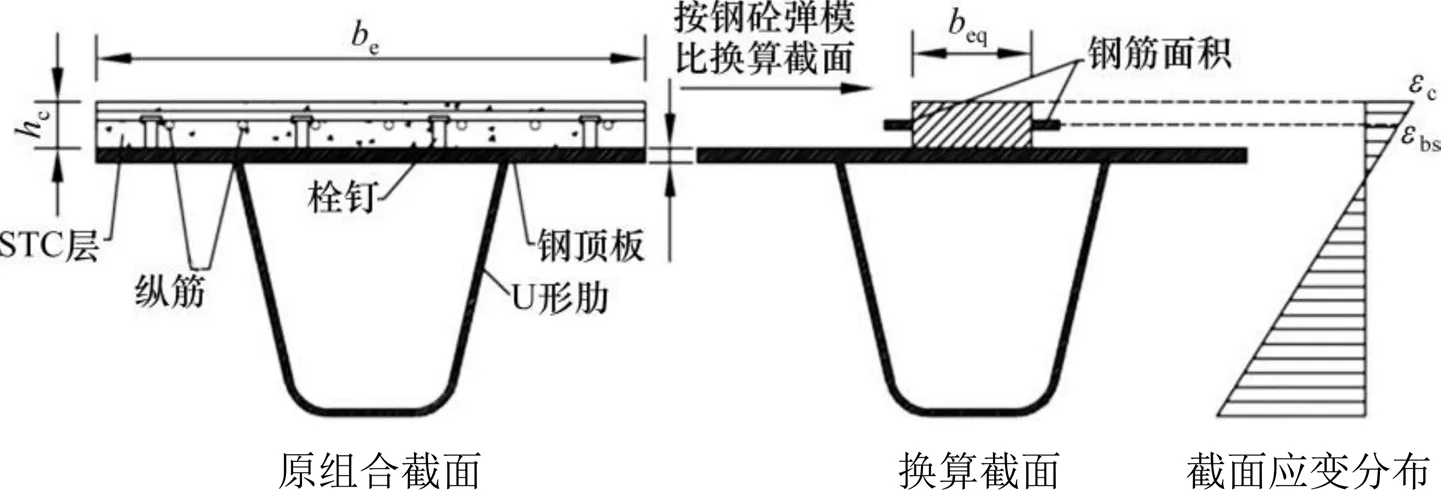
图12 组合桥面板开裂强度按弹模换算计算

经换算截面后，参照材料力学方法计算可得，疏筋段换算截面惯性矩1=1.965×10−4m4，截面形心矩STC层外表面的距离为1=0.090 674 m；密筋段换算截面惯性矩2=1.963×10−4m4，截面形心矩STC层外表面的距离为2=0.089 155 m。进一步可得，开裂荷载作用下疏筋段STC层的名义开裂强度为24.26 MPa(即荷载为543 kN时的STC表面名义拉应力)，密筋段STC层的名义开裂强度为35.69 MPa(即荷载为810 kN的STC表面名义拉应力)，当截面配筋率增大1倍时，STC层开裂强度提高47.11%。

疏筋段STC层的名义弯拉开裂应力远大于背景工程设计方要求的最大拉应力12.2 MPa，其弯拉强度还有较大富余，故适当增大STC层钢筋间距亦可满足实际工程需求。若将STC层钢筋间距从40 mm扩大到80 mm，钢筋用量可减少一半，极大地降低工程造价成本。

3 结论

为探究不同配筋率对STC−钢桥面铺装层的弯拉静力性能的影响，采用一片含2种不同配筋率的STC−钢正交异性组合桥面板足尺模型，开展了静力试验，并对不同配筋率的STC铺装层开裂强度和组合桥面板的极限承载力进行分析，得到结论为：

1) 组合桥面板受弯静力破坏试验过程可分为4个阶段：线弹性阶段、裂纹发展阶段、屈服阶段和破坏阶段。在这4个阶段中，裂纹发展阶段较为漫长。表明：组合桥面板在负弯矩作用下，具有良好的延性，并揭示了轻量化STC铺装层材料优良的抗弯拉性能。

2) 采用2种不同配筋率的STC层对正交异性钢桥面板刚度补强效果一致。在达到极限承载力之前，组合桥面板疏筋段和密筋段的刚度相差不大，直至达到极限承载力，密筋段的STC层对组合桥面刚度补强优势才得以体现。

3) 在STC−钢组合桥面结构中，STC层的弯拉开裂强度随截面配筋率增大而提高。当截面配筋率增大一倍时，STC层开裂强度提高47.11%～50.61%。

4) 采用钢筋直径为10 mm，间距为80 mm的低配筋STC层名义开裂强度为24.66 MPa，有限元结果与平截面假定计算结果相差不大，均大于背景工程设计方要求的拉应力12.2 MPa，满足其受力需求。同时方便施工，降低工程造价成本。

[1] 王春生,冯亚成.正交异性钢桥面板的疲劳研究综述[J].钢结构, 2009, 24(9): 10−13, 32. (WANG Chun-sheng, FENG Ya-cheng. Review off atiguere search for orthotropic steel bridge decks[J]. Steel Construction, 2009, 24(9):10−13,32.(in Chinese))

[2] 刘攀,盛兴跃,李璐,等.钢桥面铺装组合结构的路用性能研究[J].公路工程,2020,45(1):32−36.(LIU Pan, SHENG Xing-yue, LI Lu, et al. Research on pavement performance of steel bridge deck pavement composite structures[J].Highway Engineering,2020,45(1):32−36.(in Chinese))

[3] 李传习,李游,陈卓异,等.钢箱梁横隔板疲劳开裂原因及补强细节研究[J].中国公路学报,2017,30(3):121−131. (LI Chuan-xi, LI You, CHEN Zhuo-yi, et al. Fatigue cracking reason and detail dimension of reinforcement about transverse diaphragm of steel box girder[J].China Journal of Highway and Transport, 2017, 30(3): 121− 131.(in Chinese))

[4] 刘梦麟,邵旭东,张哲,等.正交异性钢板−超薄RPC组合桥面板结构的抗弯疲劳性能试验[J].公路交通科技, 2012, 29(10): 46−53. (LIU Meng-lin, SHAO Xu-dong, ZHANG Zhe, et al. Experiment on flexural fatigue performance of composite deck system composed of orthotropic steel deck and ultra-thin RPC layer[J]. Journal of Highway and Transportation Research and Development, 2012, 29(10): 46−53. (in Chinese))

[5] Shao X D, Qu W T, Cao J H, et al. Static and fatigue properties of the steel-UHPC lightweight composite bridge deck with large U ribs[J]. Journal of Constructional Steel Research, 2018, 148: 491−507.

[6] 李程,张法,喻满.钢-STC轻型组合结构桥面技术在株洲枫溪大桥的应用研究[J].中外公路,2017,37(6):159− 161.(LI Cheng, ZHANG Fa, YU Man. Application research of steel-STC light composite structure deck technology in Zhuzhou Fengxi bridge[J].Journal of China & Foreign Highway,2017,37(6):159−161.(in Chinese))

[7] 张哲.钢−配筋UHPC组合桥面结构弯曲受拉性能研究[D]. 长沙: 湖南大学, 2016. (ZHANG Zhe. Bending behaviors of composite bridge deck system composed of OSD and reinforced UHPC layer[D]. Changsha: Hunan University,2016.(in Chinese))

[8] 田启贤,高立强,周尚猛,等.超高性能混凝土−钢正交异性板组合桥面试验研究[J].桥梁建设,2019,49(S1):13− 19.(TIAN Qi-xian, GAO Li-qiang, ZHOU Shang-meng, et al. Research of composite bridge deck system with UHPC and orthotropic steel plate[J]. Bridge Construction, 2019,49(S1):13−19.(in Chinese))

[9] Yuan Y, Jiang X, Wu C, et al. Fatigue life assessment of orthotropic steel deck with UHPC pavement[C]// Life- Cycle of Engineering Systems. Delft, The Netherlands. Taylor & Francis Group, 6000 Broken Sound Parkway NW, Suite 300,Boca Raton,FL 33487−2742:CRC Press, 2017(2):1−10.

[10] 贺耀北,邵旭东,刘榕,等.斜拉桥双边工字钢−UHPC桥面板组合梁静力性能研究[J].桥梁建设,2019,49(1): 47−52.(HE Yao-bei, SHAO Xu-dong, LIU Rong, et al. Study on static behavior of twin I-steel-UHPC bridge deck composite girder of cable-stayed bridge[J]. Bridge Construction,2019,49(1):47−52.(in Chinese))

[11] 廖子南.钢−UHPC组合结构受弯试验与有限元模拟[D].长沙: 湖南大学, 2017. (LIAO Zi-nan. Flexural test and finite element simulation of steel-UHPC composite structure[D]. Changsha: Hunan University, 2017. (in Chinese))

[12] 李传习,石家宽,聂洁,等.平直型钢纤维掺量与长径比对超高性能混凝土性能的影响[J].硅酸盐通报,2019,38(9): 2947−2954.(LI Chuan-xi, SHI Jia-kuan, NIE Jie, et al. Effect of straight steel fiber volume content and length- diameter ratio on properties of ultra-high performance concrete[J]. Bulletin of the Chinese Ceramic Society, 2019,38(9):2947−2954.(in Chinese))

[13] 李传习,聂洁,冯峥,等.振动搅拌对超高性能混凝土施工及力学性能影响[J].硅酸盐通报,2019,38(8):2586−2594. (LI Chuan-xi, NIE Jie, FENG Zheng, et al. Effect of vibratory mixing on the construction and mechanical properties of ultra-high performance concrete[J]. Bulletin of the Chinese Ceramic Society, 2019, 38(8): 2586− 2594.(in Chinese))

[14] 李传习,聂洁,潘仁胜,等.水胶比对掺粉煤灰超高性能混凝土施工与力学性能影响[J].硅酸盐通报,2019,38(1): 14−21. (LI Chuan-xi, NIE Jie, PAN Ren-sheng, et al. Effect of water-to-binder ratio on the construction and mechanical properties of ultra-high performance concrete mixed with fly ash[J]. Bulletin of the Chinese Ceramic Society,2019,38(1):14−21.(in Chinese))

[15] 肖亚鑫,鲁乃唯,陈方怀.钢−超高性能混凝土组合板连接件的抗剪性能[J].交通科学与工程,2020,36(1):44−49. (XIAO Ya-xin, LU Nai-wei, CHEN Fang-huai. The shear capacity of steel-ultra-high performance concrete composite board connectors[J]. Journal of Transport Science and Engineering,2020,36(1):44−49. (in Chinese))

Research on static performance of lightweight STC-steel composite deck

LI Chuan-xi1, 2, LEI Zhi-jie1, 2, FENG Zheng1, 2, HE Wei-wei1, TAN Li2

(1. Key Laboratory of Bridge Engineering Safety Control by Ministry of Education in China, Changsha University of Science & Technology, Changsha 410114, China; 2. Hunan Key Laboratory of Bridge and Building Green Construction and Maintenance, Changsha University of Science & Technology, Changsha 410114, China)

To improve the economics and construction convenience of the densely-reinforced STC-steel composite bridge deck, the effect of the STC layer steel bar spacing on the bending and tensile static performance of the STC-steel composite bridge deck was studied, and the lightweight STC-Steel composite bridge deck was presented. Taking a bridge in Foshan as the engineering background, a STC-steel composite deck strip model with two different reinforcement ratios was designed and produced. Through static failure test, the STC paving of the composite bridge deck structure under the action of negative bending moment was investigated. The result show that the nominal bending tensile cracking strength of the STC layer of the lightweight STC-steel composite bridge deck with a steel bar diameter of 10 mm and a spacing of 80mm reaches 24.66 MPa, which satisfies the actual engineering design load strength requirements. The nominal bending strength of the STC layer of the combined bridge deck increases with the increase of the section reinforcement ratio. When the section reinforcement ratio is doubled, the bending tensile strength can be increased by 41.11%～50.61%. According to the load-deflection curve, the stress process of lightweight STC-steel composite bridge deck can be divided into linear elastic stage, crack development stage, yield stage and failure stage. STC layers with different reinforcement ratios have the same effect on stiffness reinforcement of orthotropic steel bridge deck. Before the ultimate bearing capacity is reached, the rigidity of the two sides of the combined bridge deck is not much different. While meeting the actual engineering needs, the distance between the steel bars of the STC layer is appropriately increased to facilitate construction and reduce the cost.

orthotropic steel bridge deck structure; reinforcement ratio; super toughness concrete; bending tensile strength; static failure test

U448.36

A

1674 − 599X(2021)01 − 0026 − 08

2020−07−11

国家自然科学基金资助项目(51778069，51808055)；长沙理工大学学术学位研究生科研创新项目(CX2020SS23)

李传习(1963−)，男，长沙理工大学教授，博士生导师。