考虑配电网级联故障的分布式电源选址方法研究

徐晓春，王栋，李佑伟，严晗，赵凤青 ，谭志海

（1.国网江苏省电力有限公司淮安供电分公司，江苏 淮安 223002；2.北京四方继保自动化股份有限公司，北京 100085）

配电网的安全稳定运行关系着经济和社会的发展，而现代配电网的智能化发展趋势和多网互联应用需求带来的安全问题不可忽视。配电网复杂性的不断增强，使得一次微小的局部扰动都可能带来大面积的级联故障[1]。近年来，国内外大规模连锁停电事件时有发生。例如，2019年7月13日傍晚，美国纽约曼哈顿中城和上西区出现大面积停电，导致美国能源公司大约40 000用户被迫断电，超过42 000用户受影响。2019年2月7日下午5点，委内瑞拉全国23个州中的21个州发生了停电，原因是向全国提供80%电力的古里水电站遭到蓄意破坏。2015年3月27日，荷兰一所变电站发生技术故障，进而引起连锁故障，导致荷兰大面积停电，对北荷兰等地区造成严重威胁。电网级联故障已成为未来智能电网安全的重大挑战。

近年来，已有许多学者利用复杂网络理论对电网级联故障现象进行了深入研究[1-3]，主要分为两大类。一类是基于电网拓扑结构分析级联故障产生的宏观机理。早在2004年，Crucitti[4]等人就研究发现电网级联故障的发生程度与网络拓扑结构有着必然联系。文献[5]基于复杂网络结构理论，研究了如何合理关闭一组传输链路以提高电网在级联故障下的鲁棒性。文献[6]运用模拟退火算法优化配电网的拓扑，并找寻级联故障下的最佳网络结构。这类仅仅考虑电网拓扑结构的研究工作，建立的模型虽然较为粗糙，但能够较好地从宏观角度解释相继故障产生的原因。另一类是基于电力潮流特性的级联故障精细建模和优化。该类工作更加关注电网的物理特性，以基尔霍夫定律为基础，结合线路的阻抗或者电抗，对配电网中的各个元件进行详细的潮流和负荷计算。例如，文献[7]根据电网中线路的有功潮流将电网抽象为加权网络，在不同边移除策略下模拟级联故障的发生过程。文献[8]构建隐形故障仿真模型，从断路器和继电保护设备的拒动或误动角度研究级联故障的发生原因。

分布式电源的选址是配电网建设和维护中的一项关键工作，其对配电网甚至整个电网的稳健运行具有重要影响[9-12]。在此之前，学者们在研究配电网电源选址问题时，主要考虑的是电网损耗等因素。例如文献[10]讨论了用于最优分布式发电规划问题的粒子群优化算法的应用模型和方法。文献[11]为改善配电系统中的电压分布，减少实际功率损耗提出了分布式发电存在情况下解决网络重构的方法。文献[12]则借助于模糊专家系统优化电源选址以进一步降低电网损耗。如何合理选择电源位置以抑制级联故障问题仍然是一个悬而未决的重要问题。事实上，配电网中节点具有不同的属性。例如，不同节点的度值或者中心性通常也不同。因此，对于级联故障而言，依据度值或中心性选择电源节点的位置必然会有不同的影响。此外，可以通过智能算法搜索级联故障条件下电源节点的最优位置。

本文结合配电网的网络拓扑结构和电力潮流特性建立了级联故障模型。基于该模型定义了级联故障条件下配电网稳健性的度量指标。提出了基于节点度和节点介数的电源节点选址方法，并通过仿真对比实验验证所提方法的有效性。进一步，使用粒子群智能算法优化发电节点的位置提高电网的鲁棒性，并从节点负荷均衡的角度给出了一种受限粒子群算法，提高了优化算法的计算效率。最后基于Price网络模型[13]，探究网络结构的异质性对电源选址问题的影响。

1 级联故障模型

本文用的电力系统模型是基于Grainger和Stevenson[14]提出的导纳模型。利用图论的方法构造网络二元组模型G=( )V,E，其中V为节点集，E为链路集。节点的总数用N表示，链路的总数用H表示，网络中的发电节点的个数用Ng表示。如文献[15]中所述，电网模型考虑四种节点：1）节点i是作为电压源的发电节点；2）节点j是消耗功率的消费者节点；3）节点k是发送电力的分配节点；4）节点h是变压器节点。电网中的基尔霍夫定律方程写成：

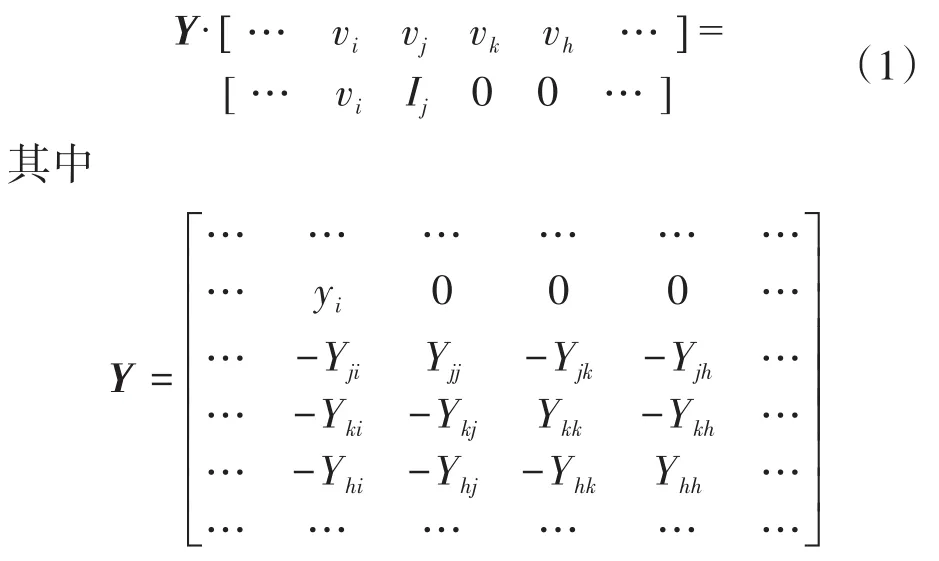
式中：vi,vj,vh,vk为四类节点的电压；Ij为消费节点j对应的电流；Y为链路的节点导纳矩阵，若节点i和节点 j之间有连接，Yij=1，否则 Yij=0，Yii=-∑i≠jYij。

从网络科学的角度研究发电节点的选址问题。为简单起见，在文中只考虑发电节点和消费节点，发电节点i对应的方程为

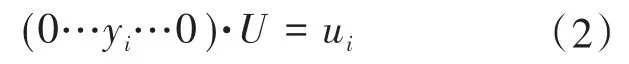
式中：yi=1；U为节点的电压集合；ui为节点i的电压。

消费节点j对应的方程为

通过式（1）可以求出节点的电压，线路上的电流可以用Iij=(ui-uj)·Yij求出。节点的负荷定义为Lp(i)=uiIoi，Ioi为流出节点i的总电流。传输线路的负荷被定义为流过该传输线路的电流，即Iij。节点负荷上界定义为Cp(i)=(1+α)ui(0)·Ioi(0)，线路的最大负荷则定义为Cij=(1+β)Iij(0)。其中参数α和β分别为节点和链路的安全裕度[15]。

级联故障过程的仿真实验步骤如下：

1）根据Y确定初始网络的节点导纳矩阵，根据式（1）可以求出每个节点对应的初始电压和各条链路的电流。

2）根据上文给出的负荷公式求出网络中各组件的初始负荷和最大负荷。

3）随机移除一条边。

4）电网的拓扑结构发生改变，重新求各组件对应的负荷。若组件（节点或者链路）超过其最大允许负荷则判定为失效件。

5）移除失效组件后，网络将分裂成若干个小的子图，如果某子图中不含发电节点，则这个子图中所有的节点都判定为失效节点。

6）重复步骤4）和步骤5），直到所有组件都在最大允许负荷范围内，网络达到稳定。

仿真过程中初始时刻移除的一条边具有一定的随机性，通常需要进行多次级联故障实验，并对观测值取平均。

2 鲁棒性度量指标

电力系统中，停电规模通常用失效节点的数量来度量。我们定义失效节点的比例PUN为

式中：Nunserved(i)为由组件i失效造成网络发生级联故障后总的失效节点数量。

由上文可知，失效节点是由两部分组成的，是故障过程中过载的节点和不含发电节点的子网中所有节点之和。因此，将电网的鲁棒性进一步定义为

该式表明电网的鲁棒性为，由一条边的移除引起的级联故障结束后剩余的正常节点所占比例的平均值。

3 基于度值、介数的发电节点选址

智能电网中，如果发电节点遭受攻击将给整个网络带来巨大的损失。因此，发电节点位置的选择将影响网络的鲁棒性和抗毁性。复杂网络理论中，度量节点的中心性的指标有许多，如节点的度值、紧密度、介数等，其中介数和度值是应用最广泛的两个指标，分别度量了节点在全局和局部拓扑结构中的影响力和重要性。节点的度是指与节点相关联的边的条数。节点的介数是指网络中所有最短路径中经过该节点的最短路径的数目占最短路径总数的比例。介数的计算公式[13]为

4 粒子群算法优化发电节点位置

为了获得最佳的发电节点的集合，建立一个优化问题，使用粒子群优化算法[16]（PSO）找寻最优解。粒子群算法是一种启发式的算法。与传统算法相比，粒子群算法具有强大的全局搜索能力，并且易于实现。算法中，随机初始化一群粒子（随机解），粒子数和每个粒子中包含元素个数分别用S和e表示，迭代过程中求出粒子的个体最优值Pbest和全局最优值gbest。粒子基于两个最优值，根据以下公式不断更新其位置：

较大的惯性系数便于粒子跳出局部最优值，有利于全局搜索；较小的惯性系数则利于对当前搜索区域进行局部精确搜索，便于算法收敛，针对PSO算法容易过早收敛和后期容易在最优值附近产生振荡的问题，采用线性变化的权重系数，让惯性系数从最大值线性减到最小值。

发电节点选址问题可以规约为0∕1背包问题[17]。因此，本文在粒子群算法求解过程中加入了0∕1背包问题的解题思想，粒子包含元素的个数设为电网的节点数，若某元素的值为1，则为发电节点；若其值为0，则为消费节点。每个粒子的约束条件是元素为1的个数等于发电节点的个数，即粒子中所有元素求和等于发电节点的个数。粒子群算法优化步骤为：

Step1：初始化，随机产生一组粒子，第i个粒子表示为Xi=[x1,x2,…,xn]。每个粒子中随机选择Ng个元素赋值为1，其他的赋值为0。

Step2：找出粒子i对应的发电节点集合，计算对应的电网鲁棒性R(G)i，并与个体最优值pbest对应的鲁棒性进行比较，若R(G)i>R(G)pbest，用Xi和R(G)i分别替换pbest(i)和R(G)pbest。同理，将R(G)i和粒子群的全局最优值R(G)gbest进行比较，如果 R(G)i>R(G)gbest，用 Xi和 R(G)i分别替换gbest和R(G)gbest，分别找出各个粒子的个体最优值和粒子群的全局最优值。

Step3：若某粒子对应的鲁棒性等于全局最优值时，对粒子进行重新赋值，以避免陷入局部最优解。

Step4：根据速度迭代式（7）产生新的速度，用式（8）更新各粒子的位置，然后对每个粒子中的元素进行排序，取最大的Ng个元素赋值为1，其余赋值为0。

Step5：检查是否达到最大迭代次数，如果没有达到，转Step2；否则，转Step6。

Step6：输出最优解，画出对应的迭代曲线图，程序结束。

基于负荷均衡的受限粒子群算法介绍如下：上文提出的粒子群优化策略仅考虑提高配电网在相继故障下的鲁棒性，并不关注实际配电网性能方面的需求。实际上，提高配电网鲁棒性可能会影响配电网供电性能。因此，对于配电网而言，在提高鲁棒性的同时保证供电性能更具实际意义。本文进一步考虑用户负荷平衡这一重要性能指标，在粒子群优化策略中加入节点负荷平衡相关的约束条件，使得鲁棒性提高的同时，节点负荷平衡也满足一定的要求。在基于负荷均衡的受限粒子群算法中，首先通过实验的手段测量鲁棒性优化过程中节点负荷方差变化的范围，并求取其期望值，然后在选择个体最优解时判断节点负荷方差是否超过其期望值。如果超过期望值，则设定其不能作为个体最优解。

网络中节点i的负荷用qi表示，节点负荷的期望为

对应的负荷方差为

5 仿真实验与分析

5.1 基于度和介数的电源选址仿真与分析

本文采用Matlab进行仿真实验，分别对IEEE 37-bus Feeder，IEEE 123-bus Feeder，IEEE 342-bus Feeder等配电网络数据[18]进行实验。实验中，为了消除其它因素对网络鲁棒性的影响，我们将发电节点的电压设置为1（标幺值），消费节点的电流设置为1（标幺值），传输线路的导纳设置为11（标幺值）。考虑到经济费用和安全裕度通常非常有限，在下面的仿真实验中设定α=0.5，β=0.2。三个网络中发电节点的个数Ng分别设为4，12和30。实验中采用三种贪婪选址方法：

1）随机选址：每个网络随机选取一组发电节点集合，计算其在相继故障条件下的鲁棒性。

2）度选址：每个网络中选出度值最大的一组节点作为发电节点集合，计算其在相继故障条件下的鲁棒性。

3）介数选址：每个网络中选取介数最大的一组节点作为发电节点集合，计算其在相继故障下的鲁棒性。

每一种选址方法都独立重复100次，并取平均结果，如图1所示。实验结果表明，选择度值大的节点集合和介数大的节点集合作为配电网的发电节点时，网络的鲁棒性比随机选择发电节点对应的鲁棒性更高。介数和度值是刻画网络中心性的重要指标，当发电节点位于更好的中心位置时，消费节点能够更容易访问到发电节点。当级联故障发生时，网络将会分裂成许多子图，含有发电节点的子图可能包含更多消费节点，而不含发电节点的子图消费节点也更少。因此，故障造成的失效节点将会更少，网络的鲁棒性更高。进一步，通过对比分析发现不同网络结构的鲁棒性提升程度不尽相同。值得一提的是，实验中我们发现大多数情况下基于介数的方法优于基于度的方法，仅在一些特殊的参数下后者有可能优于前者。

图1 不同贪婪选址方法下配电网鲁棒性的比较Fig.1 The comparison of robustness of distribution networks for different greedy location selection methods

5.2 粒子群算法仿真实验与分析

这里以IEEE 123-bus Feeder网络[18]为例进行仿真实验。网络鲁棒性随粒子群算法迭代次数的变化如图2所示。首先使用基础粒子群算法优化配电网的电源选址，同时计算每一次迭代对应的电网节点负荷的方差。粒子总数设为S=10，认知系数c1=0.7，社会学习系数c2=0.7，惯性系数w0=0.96。实验结果如图2中的虚线所示。

图2 网络鲁棒性随粒子群算法迭代次数的变化Fig.2 The change of network robustness with the increasing of itera⁃tion times in the particle swarm optimization algorithm

可以看出，网络鲁棒性随着粒子群算法迭代次数的增加而不断升高，并最终趋于平稳。通过与图1的结果进行对比得出，基于粒子群的优化方法比基于度和介数的贪婪选址方法得到的网络鲁棒性更高。但是，粒子群算法的计算代价较高，并且随着迭代次数不断增加。因此，其扩展性比贪婪选址方法要差。此外，值得一提的是，粒子群算法的初始解不同可能得到不同的优化结果。理论上，粒子数越大，迭代次数越多，优化结果更好。

进一步采用受限粒子群算法优化配电网的电源选址。实验参数与基础粒子群算法相同。结果如图2中实线所示。可以看出，受限粒子群算法对应的曲线变化趋势与基础粒子群算法类似，但是前者比后者收敛更快。换言之，受限粒子群算法比基础粒子群算法的优化效率更高，能够更高效地改善配电网的鲁棒性，并且能够保证节点负荷的平衡性。需要指出的是两种粒子群算法的时间复杂度相同。

6 配电网拓扑结构对鲁棒性的影响

对于电源选址问题，不同的配电网优化的效果不同。因此，一个有趣并且重要的问题是配电网拓扑结构对选址方法实际效果的影响。由于配电网拓扑结构具有无标度特征，本文利用无标度网络模型模拟配电网拓扑。

无标度网络常用模型为BA模型和Price模型。本文采用Price模型，因为Price模型的优点是可以调节幂律分布指数，从而可以调节网络的异质性。

利用复杂网络理论中的Price无标度网络模型生成电网拓扑结构，具体生成步骤如下[13]：

1）给定一个具有m0个节点的初始强连通网络。把每一条边所指向的节点的编号添加到数组Array中。

①生成一个完全随机数r，r∈[ ]0,1。

②如果r≥p，那么就完全随机地在数组Array中选择一个元素。

③如果r

④执行步骤①～③m次后（避免重复选取节点），把m个节点的编号添加到数组Array中，并把新加入节点和选定的节点两两相连。

该模型生成的无标度网络平均度为2m，幂律指数为2+a∕m。基于该模型，生成节点数N=118的配电网拓扑结构，并设定发电节点个数Ng=14。首先，固定网络平均度为4，而改变幂律指数。电源选址方法采用基于度和介数的方法。实验结果如图3所示，每个数据点均为100次独立实验后求平均的结果。

从图3中可以看出，配电网鲁棒性增长百分比随着幂律指数的增加呈现先增加后减小的趋势。存在最佳的幂律指数（在3.2附近）使得选址方法的效果最好。幂律指数增加，意味着网络异质性减弱。当幂律指数较小时，网络节点度分布极不均匀，并且度值或者介数较大的节点集中在网络的局部区域。将这些节点作为发电节点会导致发电节点分布过于集中，容易同时受到网络攻击，而一旦受到攻击，这些节点会与其它节点断开，使得很多攻击后的子图没有发电节点，导致总的失效节点过多。所以，随着幂律指数的增加，网络异质性减弱，度大的节点变得相对分散，网络鲁棒性增长百分比逐渐增大。当幂律指数大于3.2时，网络结构变得过于均匀，使得节点的度或者介数区分度变小，从而基于度和介数的选址方法的效果随着幂律指数的增加而变小。以上两种因素的折中导致了存在最佳的幂律指数，使得网络鲁棒性增长百分比最大。该结果也从侧面说明配电网拓扑结构对其鲁棒性具有重要影响。此外，可以看出基于度和介数的两种选址方法对应的曲线几乎重合。通过进一步实验发现，Price模型生成的网络结构中介数较大的节点对应的度值也较大。因此，这两种选址方法得到的电源位置几乎相同。在此情形下，基于度的选址方法比基于介数的选址方法更优，因为前者的计算代价远小于后者。

图3 配电网鲁棒性增长百分比随幂律指数的变化Fig.3 Robustness growth percentage vs.power-law parameter of distribution networks

7 结论

配电网中发电节点位置选择一直是一个热点问题。本文首次从配电网的鲁棒性角度入手，借助于复杂网络理论研究电源的有效选址方法，以提升配电网对级联故障的鲁棒性。提出了基于度值和介数选择发电节点位置的方法，并通过仿真实验验证了方法的有效性。为了得到最优的发电节点的位置集合，运用粒子群算法并结合0∕1背包问题的思想进行优化求解，通过实验证明了算法的有效性。进一步考虑节点的负荷平衡，给出了一种受限粒子群算法。该算法提升了粒子群的优化效率，并且能够保证一定的负荷平衡性能。最后，借助于无标度网络模型研究了配电网拓扑结构对选址方法效果的影响，发现选址方法的效果随着网络异质性的减弱，呈现先增加后减小的趋势，即存在最佳的网络结构使得选址方法的效果最优。