基于改进SIMP法的连续体结构拓扑优化方法研究*

2021-04-23李启宏李海艳

机电工程 2021年4期

李启宏,李海艳

(广东工业大学机电工程学院，广东广州 510006)

0 引言

变密度法[1]是连续体结构拓扑优化[2]的常用方法，是在工程领域中应用最广泛、商用最为成功的拓扑优化方法。变密度法采用材料单元的密度作为设计变量，其设计变量的数量很少，容易通过编程实现，计算效率也高。

SIGMUND O等[3]对基于变密度法的建模方法进行了卓有成效的研究，对不同材料中间密度惩罚方法进行了分析与对比，最终提出了固体各向同性惩罚微结构模型，即SIMP模型(solid isotropic microstructures with penali-zation , SIMP)[4];MARTINEZ J M[5]对SIMP法的理论收敛性进行了研究;STOLPE M等[6]提出了材料属性的有理近似模型(rational approximation of material properties , RAMP)，其使用有理式对材料中间密度进行了惩罚;陈祥等[7]采用RAMP法建立了基于变密度理论的优化模型。目前，SIMP法已经在不同的结构优化问题中得到了成功的应用，其引入一种假想的相对密度在0～1之间可变的材料，在一定的材料用量的条件下寻找具有最大刚度(结构的柔顺性最小)的结构材料最佳分布形式。

根据文献[8，9]的大量实验研究可发现，在使用SIMP法解决连续体结构拓扑优化问题时，其优化结构的刚度性能与力学响应分析的计算精度成正比关系。在网格规模较小时，SIMP法的力学响应分析的计算精度欠佳，导致基于SIMP法的连续体结构拓扑优化得到的优化结构的刚度偏小。增大网格规模可提高其力学响应分析的计算精度，虽然优化结构的刚度得到了提高，但受限于网格依赖性等数值不稳定问题[10]，其优化结构的细小分支增多，导致结构的可制造性很差。

针对SIMP法的这些问题，笔者对SIMP法的数学模型进行改进，在力学响应分析理论上引入新型力学数值求解方法：单元微分法(EDM)[11,12]以全体单元中心点应力应变积之和最小作为优化目标函数，再结合比例拓扑优化法(PTO)[13]对改进的数学模型进行数值优化求解；通过悬臂梁案例验证改进的SIMP法，解决连续体结构拓扑优化存在的问题。

1 SIMP法数学模型的改进

1.1 力学响应分析方法

FEM是SIMP法力学响应分析的理论基础，具有求解简便、数值计算方法成熟等优势。同时FEM也具有一定的局限性，在网格规模较小时，其计算精度不高。本小节研究的EDM是GAO Xiao-wei等针对热力耦合问题提出的一种新型力学数值求解方法，其采用离散有限单元的分析形式，且对节点受力平衡的二阶偏微分方程[14]的求解具有更高的力学分析计算精度。本研究将EDM作为SIMP法数学模型的力学响应分析方法，以提高计算精度，接下来推导其力学响应分析公式。

在节点方程配置上，传统的配置方法(traditional collocation method ,TCM)[15]通常是在所有节点中配置平衡方程，并在边界节点处添加边界条件。而EDM在微分单元的内部节点中配置微分平衡方程，在交界节点和边界节点中配置牵引平衡方程。

对于微分单元的内部节点，其微分平衡控制方程如下：

(1)

式中：bi—体力；Ω—设计域；D—单元弹性矩阵；N—微分单元的形函数矩阵；u—单元节点位移；ξ—单元内部的等参坐标，对于平面二维问题有ξ=(ξ，η)。

对于由多个单元共有的交界节点，其包含该节点的所有表面，满足牵引平衡条件：

(2)

交界节点的牵引平衡方程如下式：

(3)

对于位于结构外部的边界节点，牵引力作用于该节点，也满足牵引平衡条件。

边界节点牵引力平衡方程为：

(4)

将结构设计离散为有限单元，对整体节点进行编号，将单元的节点配置方程按节点编号叠加到相应的位置，形成全局节点配置方程组；最终方程组中的未知数在全局节点序列中进行编号，并将边界条件的指定位移和牵引力代入节点配置方程中。

最终的全局节点配置方程组形式如下：

Au=b

(5)

式中：u—整体节点的位移；b—整体节点的牵引力；A—由每个节点方程的系数构成的系数矩阵。

将式(5)作为SIMP法数学模型的力学响应分析式。

1.2 目标函数优化

SIMP法是以柔顺性最小为优化目标进行拓扑优化，其柔顺性越小，优化结构的刚度越大。提高SIMP法的力学响应分析计算精度可得到柔顺性更小的优化结构，而理论上更小的柔顺性常常与结构的合理性相矛盾。当网格规模很大时，虽然SIMP法的力学分析计算精度很高，但同时优化结构会出现很多不同的局部最优结构，表现为优化结构出现很多细小的分支。而过多的细小分支不符合实际的生产理念，其可制造性很差。

SIMP法数学模型是连续体结构拓扑优化最为常用的密度插值模型[16]，以柔顺性最小为优化目标，即追求优化结构的综合形变最小。受该思想原理的启发，以追求优化结构的最佳综合应力应变表现为出发点，再结合EDM含内部节点的特点，笔者提出以全体单元中心点应力应变积之和最小作为SIMP法数学模型的优化目标。

将单元中心点应力应变积与单元的插值密度x和材料弹性模量E相关联，则优化目标函数构造如下：

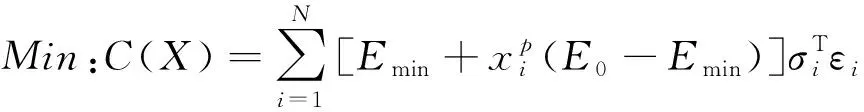
(6)

式中：xi—单元密度设计变量；N—单元数量；p—惩罚因子；σi—单元中心点的应变；εi—单元中心点的应变；Bi—单元应变矩阵；E0—实体材料弹性模量；Emin—空洞材料弹性模量。

在追求综合形变最小时，柔顺性目标函数因忽略实际生产理念，过多的细小分支导致优化结构的可制造性很差。笔者提出的目标函数更加注重优化结构每个单元的应力和应变的状态，为结合新型数值求解方法以减少细小分支数量的研究打下基础。

2 改进的SIMP法

2.1 数学模型的构建

由于前面笔者已分别用式(5，6)取代SIMP法数学模型中，原有的FEM力学响应分析理论和最小柔顺性目标函数，至此，已完成对SIMP法数学模型的改进，并提出一种改进的SIMP法(ISIMP法)，其数学模型构建如下：

(7)

式中：x—单元密度矩阵；xmin—单元密度最小值，取0.001；C(X)—优化目标函数；V—优化后的结构体积；V0—结构的初始体积；f—体积约束参数。

2.2 数值优化求解方法

PTO法是由Biyikli于2015年提出的一种新型拓扑优化数值求解算法。在应力约束问题和最小柔顺性问题中，根据每个单元所占总体应力和总体柔顺性的应力比和柔顺性比，PTO法将材料分配给相应单元。而全体单元中心点应力应变积之和目标函数涉及到最能反应受力结构力学状态的单元应力与应变，所以笔者结合PTO法对ISIMP法数学模型进行数值优化求解，在每次迭代优化中，将材料根据每个单元中心点应力应变积占全体单元应力应变积之和的比例大小，分配给相应单元。其基本步骤如下：

(1)在计算单元中心点，应力应变积占总体单元应力应变积之和的比例为：

(8)

式中：Ci—第个单元的应力应变积；Cpro—单元贡献比例；n—单元总数。

(2)在内循环中，将剩余体积按单元的应力应变积占总体单元应力应变积和的比例大小分配给每个单元，其分配公式为：

(9)

(3)当剩余体积少于0.001时，退出内循环，完成一次PTO法迭代更新。此处定义历史平衡系数α，本文取α=0.5，用于平衡当前更新得出的密度与上一次更新得出的密度，其更新方案可表示为：

(10)

2.3 应用与算法设计

为解决SIMP法在求解连续体结构拓扑优化问题时存在的缺陷，笔者将ISIMP法应用在连续体结构的拓扑优化上。基于ISIMP法的连续体结构拓扑优化方法的主要步骤为：

(1)将设计域离散为有限单元网格,并对网格节点进行编号；定义约束条件及载荷等边界条件；

(2)按照不同的节点类型配置节点方程，根据节点编号组装全局节点的EDM方程组；

(3)求解EDM方程组得到节点位移矢量，计算全体单元中心应力应变积之和目标函数；

(4)并结合PTO法对ISIMP数学模型进行数值优化求解，以更新单元密度；

(5)若连续两次迭代的单元密度最大变化小于0.01，或迭代次数达到100次，则终止迭代优化，并输出单元密度分布结果；否则重复步骤(3，4)。

基于ISIMP法的连续体结构拓扑优化流程图如图1所示。

图1 基于ISIMP法的连续体结构拓扑优化流程图

3 悬臂梁实验

悬臂梁(实验无量纲)长宽比为3∶1，梁左侧固定约束，梁的上边界施加大小为1 000的均匀分布载荷(将均匀分布载荷等效为集中力作用到节点上)。

悬臂梁拓扑优化实验的基本参数设置为：结构弹性模量E0=210，材料的泊松比μ=0.3，惩罚因子p=3，过滤半径r=1.5，材料的体积约束为0.4。

悬臂梁模型图如图2所示。

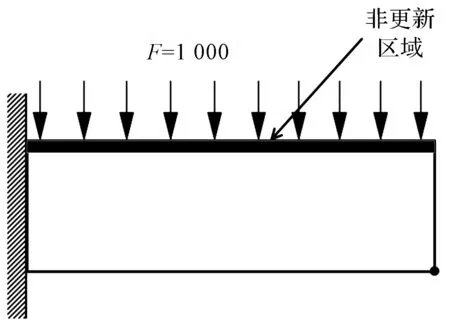
图2 悬臂梁模型图

3.1 实验基本设定

为保证悬臂梁始终受均布载荷，实验中将悬臂梁上边厚度为宽度乘0.2的区域设置为密度不更新区域，即使该区域单元密度保持为1。为保持数值求解方法的一致性，笔者基于SIMP法的连续体结构拓扑优化同样结合PTO法进行数值优化求解。为了对基于SIMP法与ISIMP法的悬臂梁优化结构的性能进行对比，该实验以优化结构的柔顺性作为对比指标。优化结构的柔顺性越小，其刚度则越大。

对基于ISIMP法的连续体结构拓扑优化的单元密度分布结果，笔者同样使用FEM进行力学分析，计算优化结构的节点位移，从而计算优化结构的柔顺性大小。

3.2 悬臂梁拓扑优化

首先，在不同网格规模下，笔者分别使用SIMP法与ISIMP法的力学响应分析理论基础，对悬臂梁进行力学响应分析，通过对比悬臂梁右下角节点的Y方向位移uy(该实验以3 000×1 000的超大规模网格进行FEM力学响应分析的结果作为假定理论值，uy=-215.298 0)，来比较SIMP法的FEM与ISIMP法的EDM在力学响应分析上的计算精度。

悬臂梁右下角节点的Y方向位移及误差如表1所示。

表1 悬臂梁右下角节点的Y方向位移

由表1可知，EDM的力学响应分析的计算误差随网格规模的增大而减小，具有良好的收敛性。与FEM相比，EDM在同一网格规模的力学响应分析中具有更高的计算精度；在网格规模较小的力学响应分析中，精度提升更为明显。

接着，在不同网格规模下，笔者分别进行了基于SIMP法与ISIMP法的悬臂梁拓扑优化实验。

基于ISIMP法，在不同网格规模下的悬臂梁拓扑优化的优化结构柔顺性的变化曲线图，如图3所示。

由图3可知，在迭代优化过程中，基于ISIMP法的悬臂梁拓扑优化的柔顺性逐步减小，具有良好的收敛性，由此可以验证ISIMP法在连续体结构拓扑优化上的可行性。

两种方法的悬臂梁优化结构的柔顺性，以及基于ISIMP法的优化结构柔顺性，相对于基于SIMP法的优化结构柔顺性的降低率，如表2所示。

表2 悬臂梁优化结构的柔顺性

结合表(1，2)数据可知：SIMP法的FEM与ISIMP法的EDM的力学响应分析的计算精度，都随着网格规模的增大而提高，悬臂梁优化结构的柔顺性都随之减小，即刚度随之增大；在同一网格规模下，EDM的力学响应分析的计算精度比FEM更高；基于ISIMP法的悬臂梁拓扑优化得到了柔顺性更小的优化结构，即悬臂梁优化结构的刚度性能得到了提升。

最后，在小规模网格和大规模网格下，笔者对悬臂梁的实验结果进行分析。

悬臂梁的拓扑优化实验结果图如图4所示。

图4 悬臂梁拓扑优化实验结果图

由表1可知，在小规模网格实验中，相比FEM，EDM的力学响应分析的计算精度优势更大。

由图4(a)可知：在网格规模为60×20实验中，两种方法的优化结构大致相同，但基于ISIMP法的优化结构柔顺性相对于SIMP法的减小了5.41%，刚度明显提升；

图4(c～d)记录了网格规模为300×100的悬臂梁拓扑优化的迭代次数为20次、40次和60次时，单元中心点应力应变积与单元插值密度的分布。由此可知，基于ISIMP法的悬臂梁拓扑优化在前40次迭代中，逐步形成稳定的传力路径区域，且在传力路径区域上的单元中心点应力应变积明显高于其他区域；再结合PTO法在数值优化求解中，将材料根据单元中心点应力应变积占全体单元应力应变积之和的比例大小，分配给相应单元的密度插值方法，那么可知在传力路径区域上，绝大多数单元将在后续的迭代优化中继续保持实体材料密度。

对比图4(b)中的网格规模为300×100的悬臂梁最终优化结构可知，基于ISIMP法的悬臂梁优化结构有效地减少了细小分支的数量，提高了优化结构的可制造性。