超深层碳酸盐岩地层水启动压力梯度研究

杨，李继强，尹冰毅，赵冠群，张俊法

(1.复杂油气田勘探开发重庆市重点实验室，重庆 401331； 2.重庆科技学院 石油与天然气工程学院，重庆 401331； 3.中国石化 石油勘探开发研究院，北京 100083)

引 言

地层水启动压力梯度会增大地层水渗流阻力[1-2]，改变储层中水相的渗流规律，进而影响水驱气藏的水侵规律和注水开发油藏的含水上升规律[3-5]。准确确定地层水启动压力梯度是准确描述储层中水相渗流规律，进而做好水驱气藏的控水治水工作和油藏的注水开发工作，从而改善水驱气藏和注水开发油藏开发效果的重要前提。

目前，国内外学者针对地层水启动压力梯度开展了一些研究，建立了一些地层水启动压力梯度与储层渗透率关系的模型[6-10]。相关研究[11-12]表明，流体性质是影响低渗多孔介质中流体启动压力梯度的重要因素，而现有模型均为启动压力梯度与渗透率的单因素模型，并未考虑流体性质对启动压力梯度的影响，致使模型预测结果差异较大，不能有效指导以地层水启动压力梯度为基础的其他相关研究[13-14]。

本文在现有地层水启动压力梯度预测模型的基础上，选取四川盆地飞仙关组超深层碳酸盐岩标准岩心，开展不同黏度条件下的地层水启动压力梯度实验测试，根据测试结果，研究地层水启动压力梯度随地层水黏度的变化规律，建立综合考虑岩石物性和流体性质的地层水启动压力梯度预测模型，以期为确定地层水启动压力梯度提供有效的方法。

1 现有预测模型评价

表1列出了现有地层水启动压力梯度预测模型[6-10]。采用现有模型计算不同渗透率岩石的地层水启动压力梯度，从计算结果(图1)来看，不同模型的计算结果差异较大。

相关研究[15-16]表明，流体在细小孔道中流动具有一定的非牛顿特征，流体的黏度越高，其非牛顿特征就越明显，宏观表现为启动压力梯度越大。从表1来看，现有地层水启动压力梯度预测模型均是与渗透率的单因素关系模型，未考虑地层水黏度对启动压力梯度的影响，致使其计算结果差异大，且基于特定地层水黏度的实验数据建立的启动压力梯度预测模型仅适用于特定气藏，适应性较差。

表1 现有地层水启动压力梯度预测模型Tab.1 Existing models for prediction of formation water threshold pressure gradient

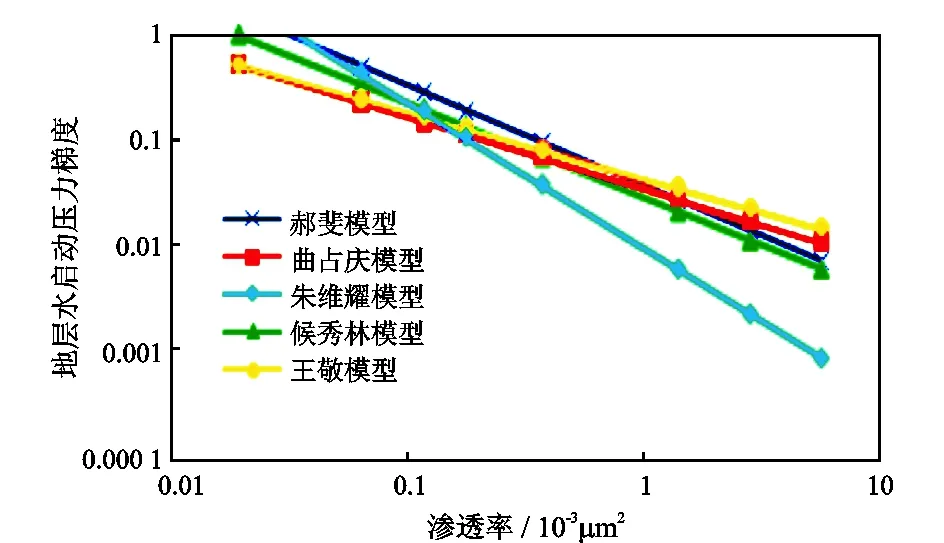
图1 现有地层水启动压力梯度预测模型计算结果Fig.1 Calculating results of existing formation water threshold pressure gradient prediction models

考虑启动压力梯度的流体渗流运动方程为

(1)

式中：v为渗流速度，μm/s；k为绝对渗透率，10-3μm2；μ为流体黏度，mPa·s；gradp为驱动压力梯度，MPa·m-1；λ为启动压力梯度，MPa·m-1。

根据流体渗流启动压力梯度的物理意义有

v=c·gradp-d。

(2)

式中：c为拟合参数，与储层物性和流体物性相关，10-3μm2/MPa·s；d为拟合参数，与储层物性和流体物性相关，μm/s。

对比式(1)和式(2)可得

λ=dμk-1。

(3)

从式(3)来看，地层水启动压力梯度与地层水黏度、岩石渗透率和拟合参数d相关，而拟合参数d与岩石渗透率与地层水黏度相关，说明地层水启动压力梯度是地层水黏度和岩石渗透率的函数。现有预测模型均未考虑地层水黏度变化对启动压力梯度的影响。

2 地层水启动压力梯度测试实验

2.1 实验原理及步骤

采用压差-流量法测定岩样不同地层水流量对应的稳定压差。根据实验测试结果，通过回归分析确定岩样的地层水启动压力梯度。

实验流程如图2所示。实验步骤为：①将实验岩心洗净、烘干后抽真空饱和地层水；②将饱和地层水的岩心放入夹持器，设置净围压为3.0 MPa，然后启动回压泵，设置出口端回压值为1.0 MPa，开启岩心夹持器加热装置，设置实验温度(不同实验温度对应不同地层水黏度)；③测定岩样不同地层水流量对应的稳定压差。

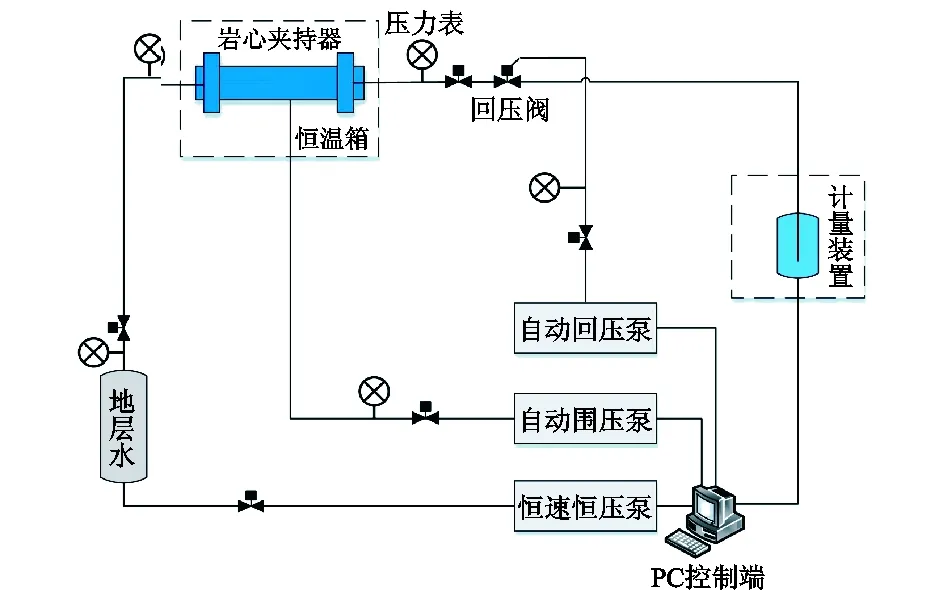
图2 地层水启动压力梯度测试实验流程Fig.2 Flow chart of formation water threshold pressure gradient testing experiment

2.2 实验条件及样品

实验采用高精度恒速恒压泵、高精度数显压力表和高精度回压阀。高精度恒速恒压泵压力精度为0.02%，流量精度0.001 mL/min，高精度数显压力表和高精度回压阀压力精度均为0.02%。实验选取四川盆地飞仙关组超深层碳酸盐岩标准岩心8块(表2)，孔隙度2.53%～9.05%，渗透率(0.018 8～5.730 4)×10-3μm2。实验用水根据地层水矿化度8.5×104mg/L配制。

2.3 实验结果及分析

根据实验测试数据回归分析得到8块岩心的地层水启动压力梯度，绘制其与岩心渗透率的关系曲线(图3)。从图3来看，地层水启动压力梯度随渗透率的降低而增大，两者在双对数坐标系下呈较好的线性关系，这表明地层水启动压力梯度和渗透率呈较好的幂函数关系。当渗透率相对较高时，随着渗透率的降低，地层水启动压力梯度会缓慢增大；当渗透率相对较低时，随着渗透率的降低，地层水启动压力梯度会急剧增大。同时，地层水启动压力梯度也会随地层水黏度的增大而增大，地层水黏度越大，启动压力梯度随渗透率的降低而增大得越快。

表2 实验岩心基础数据Tab.2 Basic data of experimental cores

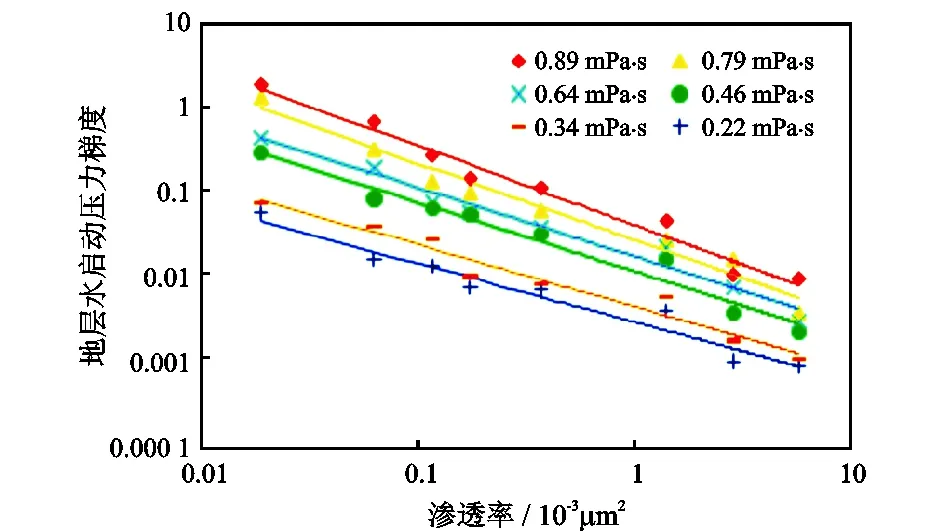
图3 不同温度下地层水启动压力梯度与渗透率关系曲线Fig.3 Relationship between formation water threshold pressure gradient and reservoir permeability at different temperatures

3 预测模型的建立

从地层水启动压力梯度实验测试结果来看(图3)，地层水启动压力梯度和渗透率呈幂函数关系，采用幂函数回归分析，建立不同温度条件下的地层水启动压力梯度与渗透率关系方程(表3)。

表3 不同温度下地层水启动压力梯度与渗透率关系方程Tab.3 Relation equations between formation water threshold pressure gradient and reservoir permeability at different temperaures

根据乘幂系数、幂指数和对应的地层水黏度数据，绘制乘幂系数、幂指数与地层水黏度的关系曲线(图4—图5)。

从图4来看，乘幂系数随地层水黏度的增大而增大，其与地层水黏度呈较好的幂函数关系，采用幂函数回归分析建立乘幂系数与地层水黏度关系方程为

a=0.046 0μw1.874 3。

(4)

式中：μw为地层水黏度，mPa·s。

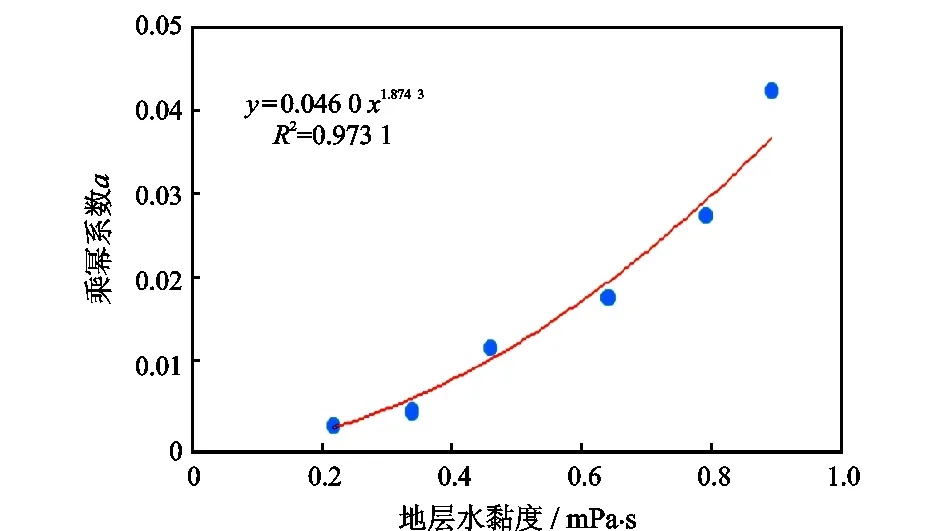
图4 乘幂系数与地层水黏度关系曲线Fig.4 Relationship between power function factor and formation water viscosity

从图5来看，幂指数随地层水黏度的增大而减小，其与地层水黏度呈较好的线性关系，采用线性方程建立幂指数与地层水黏度关系方程为

-b=-(0.350 3μw+0.608 1)。

(5)

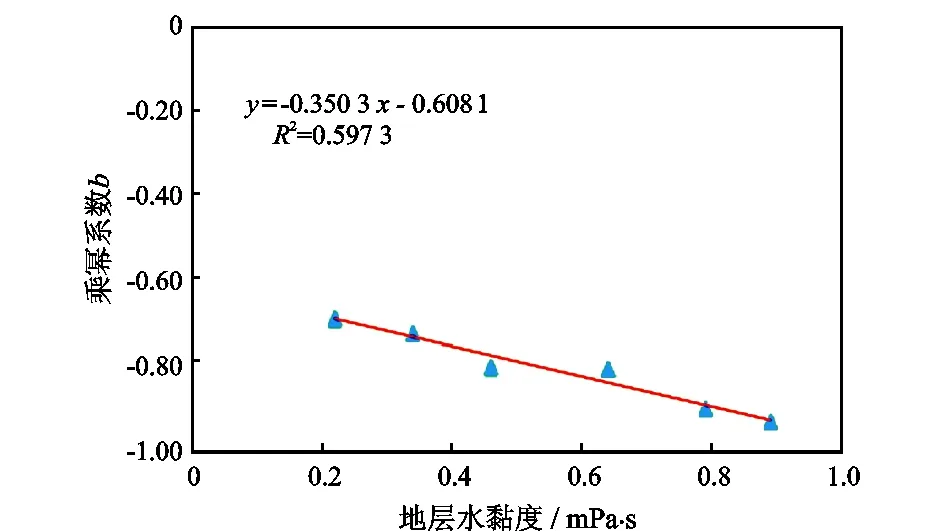
图5 幂指数与地层水黏度关系曲线Fig.5 Relationship between power function exponent and formation water viscosity

综合式(4)和式(5)，建立地层水启动压力梯度预测模型为

λ=0.046 0μw1.874 3k-(0.350 3μw+0.608 1)。

(6)

根据特定储层的渗透率和地层水黏度数据，采用式(6)可计算得到地层水启动压力梯度。式(6)综合考虑了岩石渗透率和地层水黏度两个主控因素对地层水启动压力梯度的影响，预测模型具有较强的适应性。

4 实例应用

普光气田主体气藏为带有边、底水的超深层碳酸盐岩气藏，气藏水体较为活跃，水侵较为严重[14]。气藏压力梯度为1.98～2.21 MPa/100m，属于低温系统，实测地层温度为118～132 ℃，计算对应温度的地层水黏度为0.21～0.24 MPa·s。气藏储层按物性分为Ⅰ、Ⅱ、Ⅲ三类(表4)，三类储层间互发育，从开发井钻遇气层厚度占比来看(图6)，Ⅰ类储层占比为9.6%，Ⅱ、Ⅲ类储层占比分别为32.9%、57.5%，物性较差的Ⅱ、Ⅲ类储层占比较大。随着开发的进行，气藏目前已经进入递减期(图7)，Ⅱ、Ⅲ类储层产量占比逐渐增大[17]。

表4 普光气田储层分类Tab.4 Classification of reservoir in Puguang Gas Field

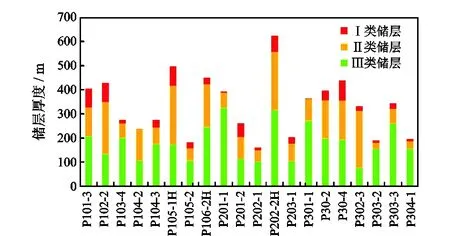
图6 普光气田主体气藏开发井钻遇储层厚度柱状图Fig.6 Reservoir thickness histogram of gas wells in Puguang Gasfield

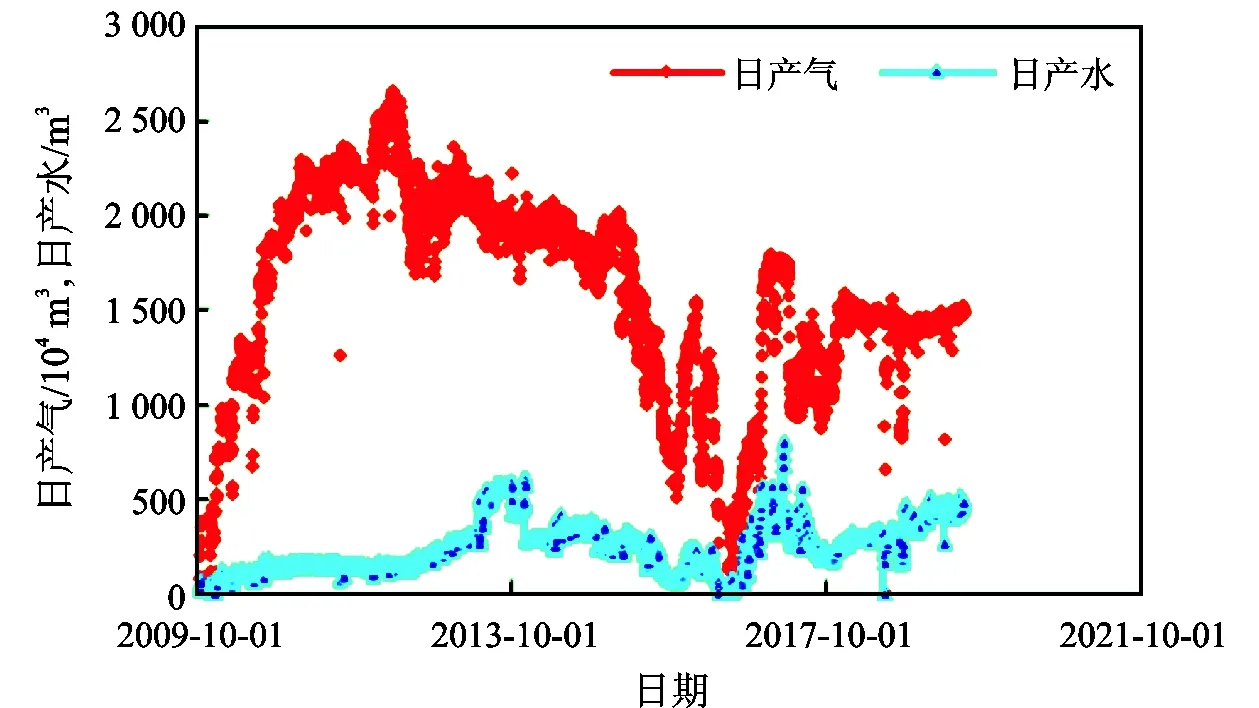
图7 普光气田主体气藏生产曲线Fig.7 Production curves of main gas reservoir in Puguang Gasfield

根据普光气田主体气藏气井测井解释成果和地层水黏度计算结果，采用新建的地层水启动压力梯度预测模型，计算普光气田主体气藏Ⅰ、Ⅱ、Ⅲ类储层在不同地层水黏度下的启动压力梯度(图8)。从图8来看，Ⅰ类储层地层水启动压力梯度较小；Ⅱ类储层地层水启动压力梯度较Ⅰ类储层明显增大，最大可达0.015 MPa/m；Ⅲ类储层地层水启动压力梯度急剧增大，最大可达0.24 MPa/m。

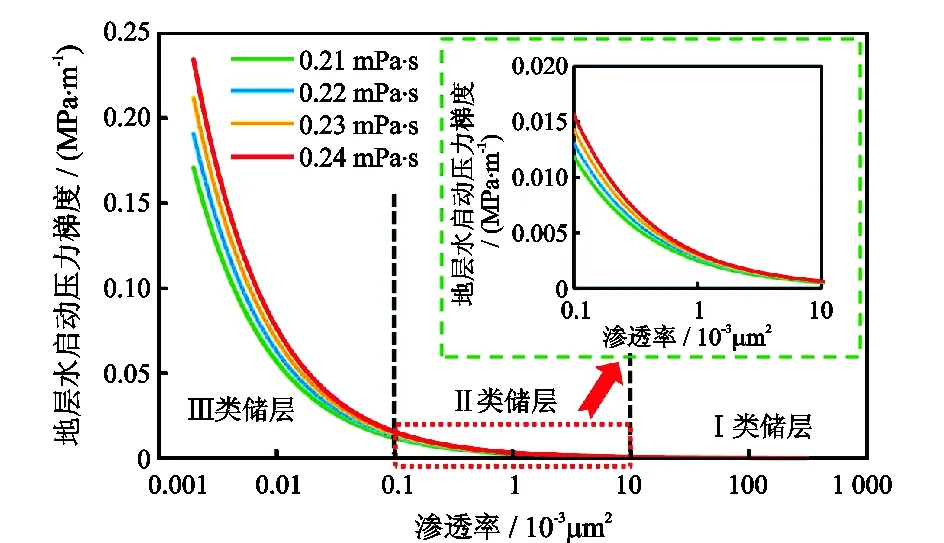
图8 普光气田主体气藏储层地层水启动压力梯度Fig.8 Formation water threshold pressure gradient of main gas reservoir in Puguang Gasfield

普光气田Ⅱ、Ⅲ类储层的地层水启动压力梯度较大，启动压力梯度会影响储层中水相的渗流规律，进而对气藏的水侵规律造成较大影响。开发后期开展气藏水侵渗流规律研究，制定气藏控水、治水措施时均需考虑地层水的启动压力梯度。

5 结 论

(1)地层水启动压力梯度是岩石渗透率和地层水黏度的函数，现有地层水启动压力梯度预测模型均未考虑地层水黏度对启动压力梯度的影响，致使其适应性较差。

(2)地层水启动压力梯度随渗透率的降低而增大，在渗透率相对较低时，随着渗透率的降低，地层水启动压力梯度急剧增大。地层水启动压力梯度随地层水黏度的增大而增大，地层水黏度越大，启动压力梯度随渗透率的降低而增大得越快。

(3)新建模型不仅考虑了岩石性质对地层水启动压力梯度的影响，也考虑了流体性质对地层水启动压力梯度的影响，具有较强的适应性。

(4)普光气田Ⅱ、Ⅲ类储层的地层水启动压力梯度较大，Ⅱ类储层最大可达0.015 MPa/m，Ⅲ类储层最大可达0.24 MPa/m。地层水启动压力梯度会影响储层中水相的渗流规律和气藏的水侵规律，在后期相关研究中均需加以考虑。