基于有限差分法的跌坎冲刷一维数值模拟
2021-04-23王新宏郎永彪倪宇航
张 雪,王新宏,董 梁,郎永彪,倪宇航
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室,陕西 西安 710048;2.青海省水利水电勘测设计研究院,青海 西宁 810001)
1 研究背景
跌坎冲刷现象广泛存在于水库溯源冲刷[1]、堤坝溃决[2-3]以及河道过度采砂[4]导致的河床冲刷等物理过程中。为了解跌坎冲刷过程及其机理,国内外学者对不同尺度跌坎进行试验研究[5],其中Bennett等[6]进行的跌坎高度为5~50 mm的小尺度跌坎冲刷水槽试验以及Robinson[7]进行的0.96~1.55 m的大尺度跌坎冲刷水槽试验比较有代表性。关于溯源冲刷问题,我国学者早在20世纪60年代就已开始研究[8-9],近年来也有很多学者针对实际水流中出现的跌坎冲刷现象进行了研究[4,10-11]。由于跌坎冲刷过程中伴随着复杂的跨临界流以及剧烈的河床变形过程,给数值求解带来了极大的困难。目前针对跨临界流模拟主要有两种方法——激波捕捉法和激波拟合法[12-13]。前者可以自动捕捉间断,但要求格式具有高性能且满足三守恒(守恒因变量、守恒型微分方程、守恒型格式),否则间断解精度不高或不正确[14];后者在间断点引入RH条件及单侧格式,可准确判断间断位置及传播速度,适合于形状陡峭的数值间断,算法复杂[15]。目前求解浅水方程的格式有Godunov 格式[16-17]、交替方向隐式格式(ADI)[18]、通量差分裂格式[19-21]和Preissmann格式等,其中Preissmann格式结构最简单且计算精度高、对步长没有限制,因而应用最为广泛[22]。但基于Preissmann格式离散的圣维南方程组在不修正的情况下无法适用于跨临界流等间断流态[23-24]。为解决上述问题,茅泽育等[25]针对Preissmann格式处理混合流时的不适进行了定性分析,认为边界条件数目与方程总数不同导致此格式无法模拟跨临界流等混合流动。吴晓玲等[26]将Preissmann格式与特征方向分解方法融合,提出了复杂流态自适应模型,并通过理想算例及实际算例验证了所建模型可模拟急、缓流交替现象。Sart等[27]根据特征方向进行局部分解的方法,对跨临界流区域进行流态划分,但如果边界河段流态复杂则无法使用该方法。
本文试图建立适用于跌坎冲刷的一维非恒定推移质输移数学模型,模拟动床情况下的跨临界流问题。对水流方程的求解,考虑到跌坎冲刷现象中存在跨临界流的问题,依据Fr大小,将河道划分为不同流态的河段,基于Preissmann格式分别离散求解。对河床变形方程的求解,采用向后差分格式离散求解,并利用水槽试验数据对模型的可靠性进行验证。本研究对于水库溯源冲刷、堤坝溃决等物理过程中出现的跌坎冲刷过程的预测具有重要的参考意义。
2 数学模型构建
跌坎冲刷通常发生在河床高程沿程忽然下降的河段,出现跌坎冲刷的河段可以概化为由3段不同底坡的河段组成,中间为陡坡河段,其上游和下游均为缓坡河段,如图1(a)所示。通常情况下,上游缓坡河段水流流态为缓流,中间陡坡河段水流为急流,下游河段水流由急流转变成缓流,有水跃现象发生。由于陡坡段水流流速突然增大,河床冲刷变形剧烈。在水流冲刷作用下上游变坡点(中间陡坡段与上游缓坡段床面交点)的位置不断向上游移动,临界水深位置和冲刷逐步向上游发展,下游河床产生淤积,最终达到冲淤平衡,如图1(b)。本文假定导致跌坎冲刷、河床冲淤变形的主要原因是推移质运动,不考虑悬移质运动造成的河床冲刷。在此前提下构建合适的推移质输移数学模型,对跌坎冲刷过程进行模拟,给出不同时刻水面线以及河床高程变化。

图1 河道跌坎水流流态及冲刷示意图
2.1 控制方程
本文建立一维非恒定推移质输移数学模型,采用的水流控制方程为水流连续方程和水流运动方程(统称为圣维南方程组),泥沙控制方程为河床变形方程,输沙率方程采用Meyer-Peter Müller(MPM)推移质输沙率公式,基本控制方程如下。
水流连续方程:
(1)
水流运动方程:
(2)
河床变形方程:
(3)
输沙率公式:
(4)
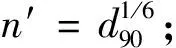
2.2 数值方法
2.2.1 圣维南方程组离散 采用Preissmann四点隐式差分格式对水流控制方程式(1)、(2)进行离散,并对离散后的非线性代数方程组进行进一步线性化处理后可以得到线性代数方程组(5)、(6)。
(5)
(6)
式中:Δzj、Δzj+1分别为第n+1时间层j、j+1断面的水位增量;ΔQj、ΔQj+1分别为第n+1时间层j、j+1断面的流量增量;A′1、B′1、…、F′2为线性代数方程组的系数,其值只与第n时间层结点值有关,通过代入第n时间层各断面流量及水位即可计算,各系数表达式见表1。

表1 线性代数方程组(5)、(6)中各系数表达式
方程组(5)、(6)是针对1个河段的两个计算断面j、j+1上写出的方程,假设将河段划分为j个断面(j-1个河段),每个断面含有两个未知数,各断面编号分别为0,1,2,…,j,每个河段可列两个方程,总共2j-2个方程,补充上、下游两个边界条件使方程组封闭,即可联立求解得出各断面不同时刻的流量和水位。
2.2.2 河床变形方程离散 采用向后差分格式对河床变形方程进行离散,离散后的方程式(3)可化为方程式(7)、(8):
(7)
(8)

河床高程Y0为已知,将水流连续方程求解得出的流量及水位代入方程式(7),采用迭代法进行计算。
2.3 跨临界流处理方法
2.3.1 数值振荡原因分析 由于在跌坎附近水流变为急流,计算区域出现急、缓流交替,水流模拟进行到6.68 s时数值发散,出现数值振荡现象,如图2所示。
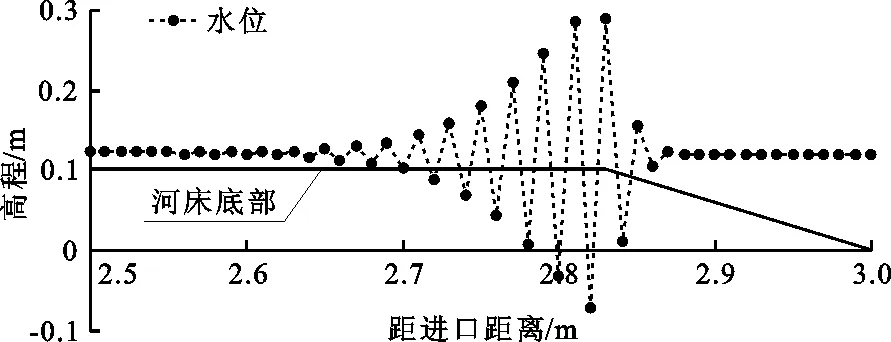
图2 跌坎水流模拟数值振荡细节图(模拟至6.68 s时)
采用水槽试验数据进行模拟计算验证[28],计算条件如下:计算长度为6 m,时间步长为0.005 s,空间步长为0.01 m,总共601个断面,分别为1#、2#、…、601#断面;跌坎坡脚位于3 m处,跌坎高度为0.1 m,坡度为30°;河床糙率为0.017,加权系数θ取0.65;初始水位为0.13 m,入口流量为5 m3/h,出口控制水深为0.05 m。模拟结果显示,260#断面之前水位维持在0.12 m左右,未发生明显波动。263#断面水位开始出现波动,263#~270#断面水位上下波动范围在0.02 m以内,270#~282#断面水位波动很大,水位误差超过0.35 m。282#~286#断面波动范围逐渐缩小,水位降到0.119 m左右。跌坎处280#、282#断面水位出现负值,程序中断无法计算。出现数值振荡的原因在于进行水流模拟时边界条件设置错误,由于跌坎处水流出现急流,而给定的边界条件只适用于缓流,急流时应给定两个上游边界条件。
根据茅泽育等[15]对Preissmann格式处理间断水流的不适定性分析,当水流流态处于单一缓流时,给定一个上边界条件和一个下边界条件(通常给定为上游流量过程线和下游水位过程线),方程数与未知数相等,可得唯一解;水流为完全急流时,只在上游给定两个边界条件(通常给定为流量过程线和水位过程线),与缓流时一样可封闭求解;当跌坎变坡点处水流由缓流过渡为急流时,入流点(缓流)给定上边界条件,方程数(2j-1)小于未知数数目2j;当水流由急流过渡到缓流时,入流点(急流)给定上边界条件,出流点(缓流)给定一个下边界条件,方程数(2j+1)大于未知数数目2j;上述两种跨临界流均不可得到唯一解,因此需要对所建立的水流模型进行修正。
2.3.2 圣维南方程组离散求解方法修正 根据上述讨论,Preissmann格式只能直接应用于每一个缓流或者急流区域,对于跨临界流区域需要增加附加方程才能求解。首先计算出第n时间层各断面的弗劳德数Fr,依据Fr沿流程变化情况,可将河段按水流流态划分为缓流河段、急流河段、水跃河段、水跌河段4种情况,确保各流段为单一流态的连续水流,针对每种情况确定不同的方程形式,从而建立求解问题的方程组。
(1)连续缓流河段或连续急流河段计算方程。如果Frj<1(j=0,1,2,…,j),即各断面弗劳德数均为缓流,各断面均可列出(9)、(10)两个方程组,给定上游边界条件为流量过程线Q=Q(t),下游边界条件为水位过程线z=z(t),采用经典的追赶迭代法即可求解各断面水位及流量。
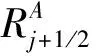
=0
(9)

=0
(10)
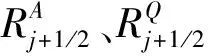
如果Frj≥1(j=0,1,2,…,j),即各断面弗劳德数均为急流,则需要给定两个上游边界条件,即流量过程线Q=Q(t)和水位过程线z=z(t),通过迭代法进行求解。
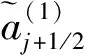
(11)
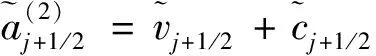
(12)
其中:
(13)
(14)
a(1)=v-c
(15)
a(2)=v+c
(16)
式中:a(1)为微波向上游传播的速度,m/s;a(2)为微波向下游传播的速度,m/s;j+1/2为河段;j、j+1为断面;v为断面平均流速,v=Q/A,m/s;c为微波的相对速度,m/s。

(17)
α(Δzj+2bj+2-ΔQj+2/2cj+2)+(1-α)(Δzj+1bj+1-ΔQj+1/2cj+1)=0
(18)
(19)
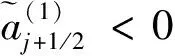
(3)水跌河段计算方程。如果Frj<1、Frj+1≥1,则有临界点(Fr=1)存在,出现水跌现象,但水流仍处于连续状态,在此河段上仍然可以使用水流连续方程及水流运动方程。此河段上游边界为缓流,下游边界为急流,上游给定流量过程线,由于方程数为(2j-1)小于未知数数目2j,需要补充一个方程作为下游边界条件即可求解。临界点处a(1)=0,a(2)=2c,补充方程为:
α(Δzj+1bj+1-ΔQj+1/2cj+1)+
(1-α)(Δzjbj-ΔQj/2cj)=0
(20)
(21)
通过流态将整个河段划分,不同区域采用不同的方程求解,避免了Preissmann格式不能适用于跨临界流的缺点。
2.4 边界条件及求解方法
在跨临界流问题中将河道划分为不同流态的河段,依据不同流态提出相适应的边界条件。河段为缓流时给定上游流量过程线和下游水位控制线,急流时给定两个上游边界条件,即水位和流量。水流为水跃和水跌时需加入附加方程进行求解。
求解方法采用非耦合解法,首先考虑水动力因素求解水流控制方程,其次将水流方程中计算得到的水位、流量带入泥沙方程进行迭代求解,此方法大大减少了计算难度。
3 模型试验验证
3.1 基本资料
本文对跌坎冲刷问题的模拟采用水槽试验数据进行验证[28]。矩形断面水槽长度为6 m,水面宽度为1 m,跌坎末端位于水槽中点,跌坎坡度为30°,跌坎高度为0.1 m,泥沙颗粒中值粒径采用0.6 mm(采用均匀沙),河床糙率取0.017;时间步长取0.005 s,空间步长取0.01 m(即断面总数为601),河床底部糙率取0.017,加权系数θ取0.65;入口流量为5 m3/h,上游水深为0.027 m,跌坎下游水深控制变化过程见表2,其中t为时间,Z为水深。河床底部高程由公式(22)给定,x为距进口里程方向的距离。

表2 模型试验跌坎下游水深控制变化过程
(22)
3.2 结果分析
3.2.1 水流流态分析 根据上述水槽基本资料及各参数对本文所建模型进行了验证计算,120 s时各断面Fr分布情况见图3。

图3 水槽试验120 s时各断面Fr分布模拟计算结果
由图3可以看出,在260#断面(距离进口2.6 m处)之前,各断面Fr均小于0.3,上游断面水流处于均缓流状态,260#~280#断面Fr迅速增长接近于1,出现这一剧增的原因在于跌坎的出现。281#断面Fr为0.978,282#断面Fr为1.823。281#~282#断面中间经历缓流到急流的过渡,出现跨临界流,该位置正处于跌坎上游边坡点附近。283#~292#断面Fr均为大于1且不断增大到4.856,293#断面Fr开始剧烈下降,294#断面Fr急剧降到0.5左右,水流流态变为缓流,该位置处于跌坎下游坡脚处,水流从急流转变为缓流出现水跃现象。之后水流一直处于缓流流态,最终Fr维持在0.05基本不变。整个冲刷过程中水流流态从缓流到急流再到缓流,期间出现了水跃、水跌等水力现象,表明经过修正后的模型可以很好地模拟复杂流态的转变。
3.2.2 水面线及河床底部高程分析 图4为t=0、t=5 s、t=10 s、t=50 s以及t=120 s时的跌坎冲刷模拟计算结果,其中包括水面线计算值与实测值、河床底部高程计算值与实测值。初始时刻水面线及河床底部高程见t=0时刻(图4(a)),水面高程保持在0.13 m,河床底部高程由公式(22)给定。跌坎冲刷进行到5 s时(图4(b)),水面线稍有下降,可以看到水面线在上游变坡点处(284#断面)出现明显降落,水位开始出现波动,底部河床还未见明显冲刷。冲刷进行到10 s时(图4(c)),上游变坡点处水位沿河床边界大幅下降,河床底部也开始出现冲刷,下游水位降到0.08 m左右。冲刷到50 s时(图4(d)),坡脚处水位已降到0.03 m左右,水位沿程下降,河床大幅冲刷,且冲刷范围不断向上游发展,下游河床发生淤积,跌坎坡度变缓。模拟进行到120 s时(图4(e)),上游水位降到0.11 m左右,下游水位降到0.01 m,上游冲刷及下游淤积速度明显减慢,基本达到冲刷平衡。本文在水动力模型中考虑河床冲淤变形,修正后的模型在模拟动床跨临界流也可以适应复杂流态的转变,所建模型对于跌坎冲刷的模拟符合其实际物理现象。
图5为不同时刻跌坎前后局部水面线高程及河床底部高程。由图5(a)可看出,跌坎附近水面线随着冲刷时间逐渐下降,跌坎上、下游水位高差不断增大,且有明显的间断点。t=80 s时水面线在下游坡脚处(3.0~3.5 m断面)低于t=120 s时的水面高程,其原因是此时下游坡脚处发生冲刷,此处河床产生淤积所致。由图5(b)可看出,冲刷初期河床底部高程变化剧烈,随着时间的延长冲淤速度逐渐变慢;在冲刷作用下跌坎坡度逐渐变缓,冲刷向上游发展,下游河床发生淤积,最终达到基本稳定,表明了跌坎冲刷的发展过程及特点。

图5 不同时刻跌坎前后局部水面线高程及河床底部高程
3.2.3 计算精度分析 将t=120 s时跌坎前后局部水深及河床冲淤厚度的计算值与实测值进行对比,见表3。由表3可见,试验水槽内水深最深处只有1.5 cm,各断面水深计算值的绝对误差为0.06~0.12 cm,相对误差为-6.7%~40%。河床冲淤厚度绝对误差最大为-0.90 cm,相对误差最大为24.3%。由于水深很小,试验本身测量难度大,实测数据也有一定的误差,导致计算值与实测值的误差偏大,但是模拟趋势符合实际情况,从图4中不同时刻跌坎冲刷模拟结果可以看到,所建模型对于水槽试验中跌坎冲刷过程的模拟比较准确。
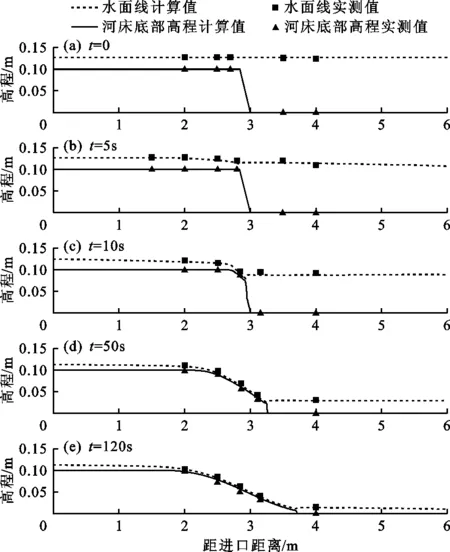
图4 不同时刻跌坎冲刷模拟计算与试验实测结果
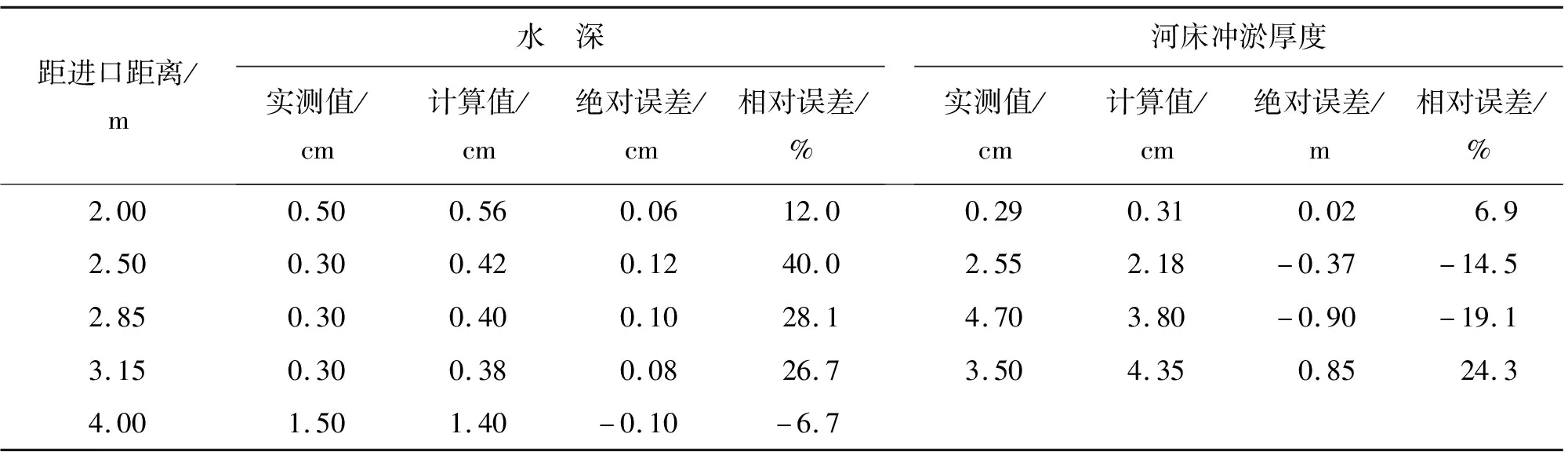
表3 跌坎前后局部水深及河床冲淤厚度计算值与试验实测值对比(t=120 s)
4 结 论
跨临界流现象经常出现在溃坝水流及水库溯源冲刷等实际工程问题中,其研究价值也得到了国内外学者的关注。本文采用改进的Preissmann格式建立了一维水沙动力学模型,模拟了跌坎冲刷处水沙运动情况,得到以下结论:
(1)建立了跨临界流跌坎冲刷一维非恒定推移质输移数学模型。该模型可以计算跌坎冲刷河段跨临界流水面线、河床纵剖面等随时间的变化过程。
(2)采用经典Preissmann格式模拟跨临界流会出现数值振荡现象,修正后的模型通过弗劳德数Fr识别间断点位置,据此将水流划分为急流、缓流、水跃以及水跌4种流态,针对4种流态河段采用不同的离散方程求解,通过河段边界水流流态提出合适的边界条件,迭代进行求解。通过水槽试验数据验证,所建模型可以很好地模拟复杂流态的转变,证明了经典Preissmann格式通过修正模拟跨临界流的可行性。
(3)利用跌坎冲刷水槽试验数据,对所建模型进行了验证计算。计算结果表明,该模型可以反映跌坎冲刷过程中跨临界流的各种复杂水流现象,以及陡坡河段由于泥沙冲淤造成的底坡逐渐变缓、长度逐渐增加等河床变形现象。对比水槽试验实测值与模型计算值可知,各断面计算水位和河床高程与实测值较为符合,说明所建模型具有一定的计算精度。
