基于多层规划的武汉城市圈水量-水质耦合配置研究

颜鹏东，陈义忠，张佳锋，李 皓，何 理

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.河北工业大学 经济与管理学院，天津 300401；3.中国科学院国家空间科学中心，北京 100190；4.中南大学 机电工程学院，湖南 长沙 410083)

1 研究背景

武汉城市圈作为我国中部经济发展的引擎，需要大量的水资源来支持工业生产活动和生态环境建设[1]。随着人口和经济的持续增长、城市化以及伴随而来的环境变化引发了供需不匹配、用水冲突、水污染等诸多问题，水资源已成为制约该城市圈经济可持续发展的瓶颈[2]。在气候变化和人类活动的影响下，极端气候事件发生的可能性增大，也加剧了城市圈水资源供需的不平衡[3]。《中华人民共和国国民经济和社会发展第十三个五年规划纲要》中明确指出要提高资源开发利用效率，降低水资源消耗，这必将对城市的可持续发展和水资源的合理配置提出更高的要求。城市圈水资源优化配置是一个涉及多利益主体的复杂过程，是区域经济发展与生产要素在空间上的优化组合。如何在兼顾经济竞争力和环境可持续性的前提下开发高效和综合的优化方法，以提高城市圈水资源利用效率已成为目前该领域研究的重点[4]。

区域水资源优化配置的实质是从分配效率和利用效率两个方面提高水资源的配置效率，其目的是促进区域环境、社会和经济的全面协调发展[5]。目前国内外学者已取得了一定成果[6-8]。例如，Kumar等[9]建立了综合经济和环境模型，为我国流域综合管理提供了科学的决策信息，结果表明，不同利益相关者的参与是促进水资源综合管理成功的关键之一。Roach等[10]在复杂气候变化和人口增长模式下，为水资源系统的中长期管理提出了具有弹性的指标，提出评估水资源管理系统弹性指标应同时使用多个指标。这些研究主要集中在统计确定性方法上，以解决污染物排放、多个利益相关者的冲突和需求的相关管理问题。针对水资源管理系统的复杂性，也开发了多种不确定性优化方法，如随机规划[11]、模糊规划[12]和区间规划[13]。Li等[14]提出了考虑生态需水的多阶段模糊随机规划水资源管理方法，结果有助于以交互方式确定目标的满意度和约束的可行性，使决策者能够产生一系列的替代方案。张成龙等[15]引入模糊变量、概率分布和区间数来表示农业灌溉系统的多重不确定性，建立了黑河中游区间两阶段模糊可信性约束规划模型，模型的结果可为黑河中游地区农业水资源优化管理和作物种植结构优化提供不同可信性置信水平下的水资源优化管理方案。

然而以往的水资源优化配置研究大多将复杂的水资源管理系统简化为经济或环境控制型的单目标规划问题[16]。虽然水资源管理系统的多目标规划在一定程度上能够综合体现系统的环境和经济效益，但往往忽略了不同利益相关者之间的等级结构。事实上，水资源管理系统会受到水资源可用性、社会经济活动和不同利益主体间互馈关系等诸多因素的影响，而传统的水资源优化方法难以反映不同利益主体间复杂的制衡过程[17]。双层规划方法能够客观反映不同利益主体间的互馈响应关系。例如，Wang等[18]建立了基于双层规划的用水结构优化模型并应用于我国西北地区，其结果可以根据决策者的风险态度从模型中找到配水决策方案，以支持社会和谐和经济发展。张鑫等[19]建立了榆林市水资源承载力双层规划模型，其模型考虑了决策者和执行者之间的利益关系，结果表明，榆林市整体用水结构处于高收入国家水平，但局部地区农业用水比重偏大。尽管双层规划在处理简单的主-从问题时具有显著作用，但是与水资源规划有关的目标并不仅限于两个层面[20]。例如一些决策者(如环境部门)的目标是实现最低的污染物排放，一些决策者(如经济部门)希望将更多的水量用于实现经济发展，一些决策者(如水管理部门)希望将水利用所获收益分配尽可能均等化。因此，需要提出一种适当的方法来确定能够实现多层次决策者提出的综合目标的水资源规划战略。然而，无论是双层还是多目标方法，都不能有效地处理这样一个多层次决策问题。近年来，多层规划因其处理复杂的主-从关系的能力而备受关注[21]。它不仅能有效解决传统双层规划模型受目标函数数量限制的问题，而且能客观反映多层次决策者之间的决策交互。然而由于多层规划的几何性质相较于单层规划更加复杂，属于NP-hard问题，所以也增加了其求解难度[22]。

受经济社会发展过程复杂性的影响，区域水资源系统呈现多层次性和多重交互性。由于决策视角、水资源数量和水环境质量的细微扰动均会直接或者间接作用于武汉城市圈水资源系统管理，因此科学反映系统决策者的层次结构、量化水量水质状态对系统经济效益和环境效益的影响、提供交互博弈视角下的城市圈水资源管理方案有助于为武汉城市圈可持续发展提供科学水政策。针对以上科学问题，本文提出了基于多层规划的武汉城市圈水资源水环境系统优化管理模型。该模型在区域水量供需状态科学预测和水资源承载响应特征识别基础上，集成了水资源配置系统的社会-经济-环境目标，并结合交互式算法和模糊满意度算法，利用Lingo编程软件对多层规划模型进行求解。通过不确定性分析以及与传统模型计算结果的对比，验证了该多层规划模型结果的鲁棒性与优越性。

2 研究区域概况与数据来源

2.1 研究区域概况

图1展示了武汉城市圈的土地利用及水系分布。武汉城市圈地处湖北省东部，总面积5.78×104km2，主要包括武汉、黄石、鄂州、黄冈、孝感、仙桃、天门、潜江等城市。其占湖北省GDP和人口总量的60%，是湖北经济发展的重点区域，也是中部崛起的重要战略支点。武汉城市圈属亚热带季风气候，雨量充沛，区域水系发达，河流湖泊众多，淡水资源总量为333.06×108m3。但其水资源时空分布不均匀。年降水量主要集中在每年4-9月，由东南至西北逐渐减少。此外，武汉城市圈是湖北省人口最密集、经济最发达的地区。虽然水资源总量丰富，但由于人口众多，人均水资源优势并不明显。随着工业化、城市化的发展以及工业和居民用水量的增加，会导致水资源短缺[23]。更为严重的是，大部分河流和湖泊由于大量废水的排放而受到污染[24]，且由于武汉城市圈是多个城市的集合，其内部不同利益主体的相互制约关系使水资源配置更加复杂。因此，迫切需要通过多个决策者建立合理的水资源配置方案，以协调供需矛盾，改善水环境质量。

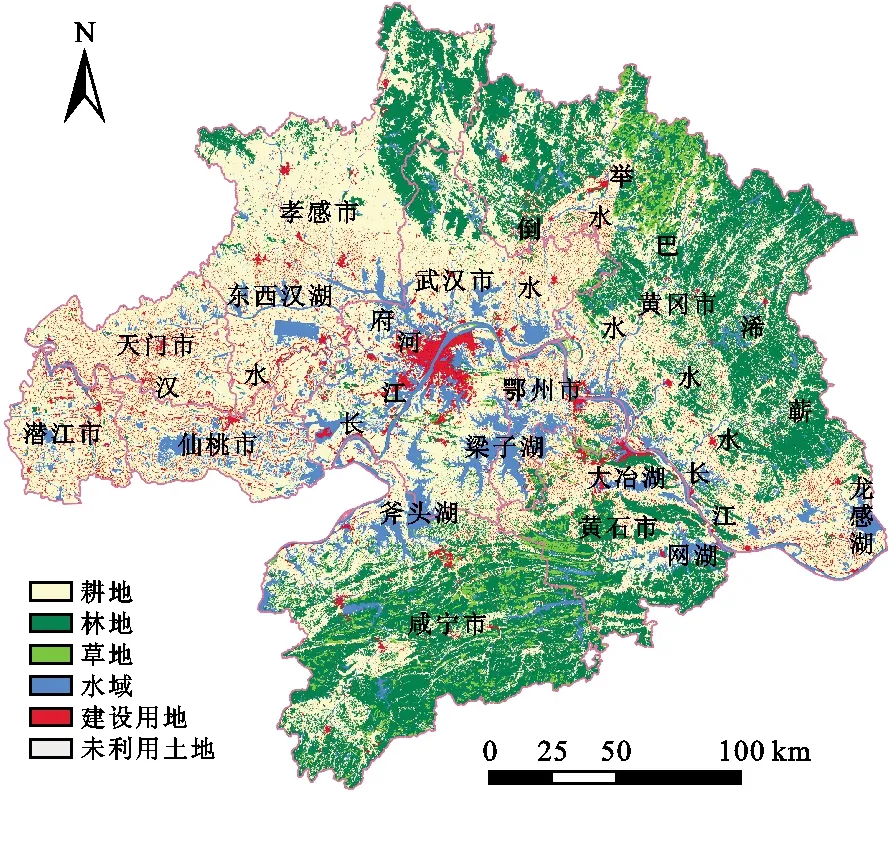
图1 武汉城市圈土地利用及水系分布

2.2 需水预测与水足迹代理方程率定

本研究预测了受用水效率、节水水平等多重因素影响的生产和生活用水定额。这些预测是通过考虑当地经济和社会发展、水资源需求控制、产业结构调整、节水措施实施、用水变化和供水效率等方面的差异来确定的[25]，数据主要来源于历年湖北省水资源公报与湖北省统计年鉴。其中各产业需水量预测方法参考文献[26]、[27]，图2为两个规划期2020和2025年各产业需水量预测结果。考虑到武汉城市圈未来的社会经济水平和生态环境需求具有高度的不确定性。因此，后续所开发的多层规划模型将在需水预测的基础上，考虑水资源管理系统的复杂决策过程，以期实现武汉城市圈水资源的绿色开发，从而促进社会、经济和环境的协同发展。

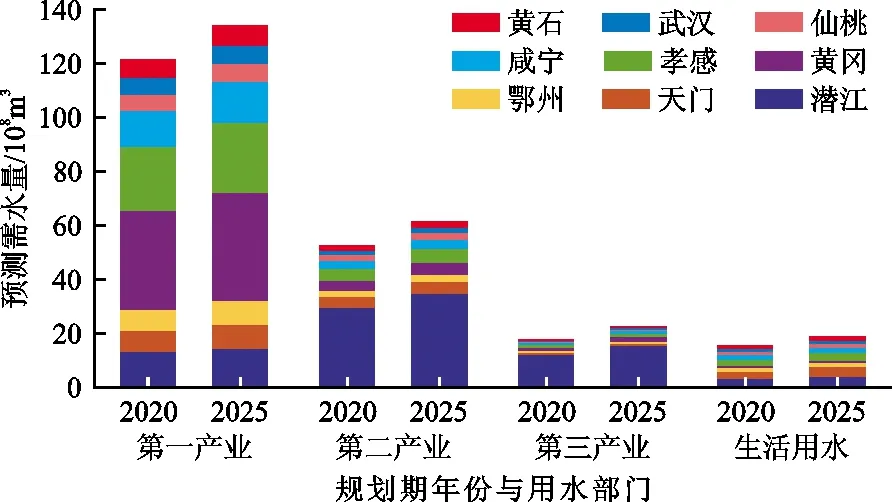
图2 2020和2025年武汉城市圈各产业部门需水量预测结果

考虑到水足迹直接指示产品生产全过程中水的消耗，将水足迹与水承载力纳入模型框架。水足迹是指人类生活生产和自然环境所需的水资源面积。水足迹计算方法借鉴文献[28]、[29]。将武汉城市圈9个城市2000-2015年水足迹与水承载力进行统计计算，建立水足迹的代理方程，图3为水足迹代理方程拟合图，其中，代理方程以生产用水量占总用水量的比例作为自变量，人均水足迹作为因变量。经二次函数最小二乘拟合的拟合度R2=0.537。在下文中，水足迹将作为一个重要的约束条件。

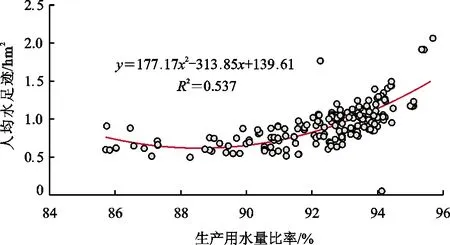
图3 2000-2015年武汉城市圈水足迹代理方程拟合图

3 武汉城市圈水量-水质耦合配置多层规划模型(NLP-BES)

3.1 水资源配置决策系统

在水资源配置决策过程中，不能将环境、经济、社会等因素聚合成单一的目标函数或归置于同一决策层面，而应该将其综合、分层次地整合入模型框架中。为解决这类问题，本研究建立了一个多层次决策模型。考虑到水资源利用过程中的环境影响(尤其是COD和氨氮排放)已成为水资源有效利用的制约因素，本研究将水资源配置及利用过程中有关的COD与氨氮排放控制目标作为模型的上层目标；将水资源配置所产生的经济效益优化目标置于模型的中层；同时，考虑到水资源配置收益的均等化分配是保持社会稳定、促进城市圈协同发展的重点，所以引入水资源配置收益的均等化目标作为模型的下层目标。然而，在水资源配置决策过程中，上述3个目标函数所产生的水资源配置方案偏好往往是相互冲突的，为了应对不同决策者之间的利益矛盾，在水资源配置多层次决策过程中，上层决策者需要充当领导者，并且必须考虑到中层模型和下层模型的决策，然后调整和优化自己的配置方案，而处于相对服从地位的决策者需要在上级决策者的方案提出后，根据自身发展需要做出最优决策方案。具体水资源配置系统见图4。

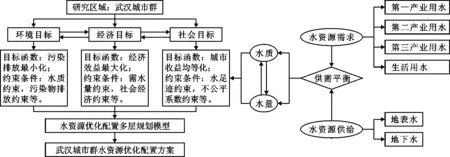
图4 武汉城市圈水资源配置系统示意图

3.2 环境目标函数及约束条件

选取排放废水中的重要污染因子COD与氨氮的含量为主要指标，以污染物允许最大排放量约束、废水设计处理能力和二元变量约束、水质约束为上层约束条件。

目标函数中生态环境子目标表达式为：

wsj,i,k·DS·CDSg,k+wtj,i,k·DT·CDTg,k+wlj,i,k·DL·

CDLg,k)·(1-ηi,g) (∀i,j,g,k)

(1)

式中：j为水源，j=1代表地表水，j=2代表地下水；i为行政区，i=1～9分别代表武汉、黄石、鄂州、黄冈、孝感、咸宁、仙桃、潜江、天门；g为污染物种类，g=1代表COD，g=2代表氨氮；k为规划期，k=1代表2020年,k=2代表2025年；ESN为COD与氨氮排放总量，104t；wp、ws、wt和wl分别为第一产业、第二产业、第三产业和生活用水量，m3；DP、DS、DT和DL分别为不同用水部门的污水排放系数；CDP、CDS、CDT和CDL分别为不同用水部门排放废水中的污染物浓度，mg/L；η为污染物的去除率，取85%。

约束条件为：

(1)污染物排放及处理约束，即污染物和废水排放量不应超过环境限制。

wtj,i,k·DT·CDTg,k+wlj,i,k·DL·CDLg,k)·(1-ηi,g)

≤MDDi,g,k(∀i,j,g,k)

(2)

式中：MDD为各个地区的污染物排放量上限，104t。

(2)处理能力和二元变量约束。污染物和废水排放量必须小于或等于最大设计处理能力，同时可以考虑一些扩建方案。

(3)

式中：STC为不同地区的污水处理能力，m3/d；T为规划期时长，d；es为污水处理厂的扩容量，m3/d；m为污水处理厂的扩容方案；z为二元变量，其值为0(不进行扩容)或1(进行扩容)。

(3)水质约束。水污染的经济损失是指水环境质量下降导致的水服务功能的破坏，进而造成的经济损失。这种损失通常包括两个方面：①由于水质不达标，或水质暂时达标但有恶化趋势，为了避免由此造成的污染危害，水管理者和用水者支付了防御费用；②水污染给用水者造成的直接经济损失[30]。

Qmini≤Qi≤Qmaxi(∀i)

(4)

(5)

(6)

(7)

式中：Qmin和Qmax分别为地区河湖平均水质变化的最小值和最大值；Q为地区河湖平均水质，为整数型变量；ωp、ωs和ωt分别为第一产业、第二产业和第三产业污染造成的经济损失率；J为水污染对各个计算分项的最大经济影响损失率(J1代表第一产业；J2代表第二产业；J3代表第三产业)，其反映了水污染达到最严重情况下，对社会经济各个计算分项可能带来的最大经济损失率[30]，在本研究中J1、J2和J3分别确定为0.45、0.04和0.11。

3.3 经济目标函数及约束条件

中层目标函数为武汉城市群供水所带来的净经济效益最大化，其约束条件包括粮食产量约束、用水部门需水量约束、可供水量约束、区域人口数量和社会经济约束。

目标函数中经济效益子目标表达式为：

(8)

式中：BEN为系统合理水资源分配带来的经济效益，元；BP、BS、BT和BL分别为第一产业、第二产业、第三产业和生活用水效益系数，元/m3；CP、CS、CT和CL分别为第一产业、第二产业、第三产业和生活用水成本系数，元/m3；um、un、uo和up分别为第一产业、第二产业、第三产业和生活用水公平系数(即优先得到供水的次序)；UEC为单位扩容成本，元/m3；USC为不同时期的单位污水处理成本，元/m3，其与各地区水质(Qi)级别有关，水质级别越高，相应的单位处理成本就越高；GP、GS和GT分别为第一产业、第二产业和第三产业总产值，元。

约束条件为：

(1)用水部门需水量约束。在这个约束条件中，考虑了下限值和上限值，以解决水需求的不确定性。

(9)

式中：WPMIN、WSMIN、WTMIN和WLMIN分别为第一产业、第二产业、第三产业和生活用水的最小用水量，m3；WPMAX、WSMAX、WTMAX和WLMAX分别为第一产业、第二产业、第三产业和生活用水的最大用水量，m3。

(2)供水量约束，即各水源向各用水部门的总供水量不得超过可用水量。

wpj,i,k+wsj,i,k+wtj,i,k+wlj,i,k≤Wj,i,k(∀j,i,k)(10)

式中：W为不同水源的水量约束，m3。

(3)粮食产量约束，即粮食生产用水应大于最低产量要求。

(11)

式中：UFW为单位粮食生产量的耗水量，m3/t；FM为地区最低粮食产量，t。

(4)社会经济约束，即经济和人口需要被限制在一个合理的范围内。

(12)

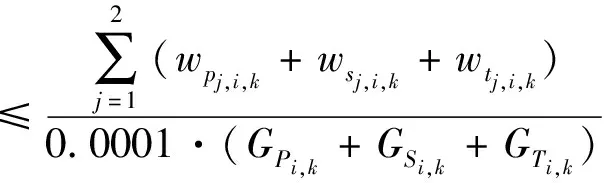
≤GDWUi,k(∀i,k)

(13)

GPLi,k≤GPi,k≤GPUi,k(∀i,k)

(14)

GSLi,k≤GSi,k≤GSUi,k(∀i,k)

(15)

GTLi,k≤GTi,k≤GTUi,k(∀i,k)

(16)

POLi,k≤POi,k≤POUi,k(∀i,k)

(17)

式中：POWL和POWU分别为地区最小和最大的人均生活用水量，m3；PO为地区人口数量；GDWL和GDWU分别为最低和最高的万元GDP用水量，m3/(104元)；GPL、GSL、GTL(104元)和POL分别为各经济和人口指标的下限；GPU、GSU、GTU(104元)和POU分别为各经济和人口指标的上限。

3.4 社会稳定目标函数及约束条件

下层目标函数为不同城市间单位水资源配置所获得的经济效益均等化，其约束条件为人均水足迹约束与收益不公平性上限约束。

目标函数中社会稳定子目标表达式为：

(18)

其中：

(19)

(20)

式中：EA为不同地区不同时期的单位水资源使用收益，元。

约束条件为：

(1)人均水足迹约束。

f(wpj,i,k,wsj,i,k,wtj,i,k,wlj,i,k)≤PWFi,k

(21)

(22)

f(wpj,i,k,wsj,i,k,wtj,i,k,wlj,i,k)=177.17(SEi,k)2-

313.85SEi,k+139.61 (∀i,k)

(23)

式中：f为水足迹和用水量的代理方程；SE为不同地区不同时期的生产用水与用水总量的比值；PWF为不同地区不同时期的最大人均水足迹，hm2，其值取为3 hm2。

(2)收益不公平性上限约束，即城市间单位水资源配置所得的经济效益不能超过一定限值。

(24)

规划期2020和2025年各用水部门用水污染物浓度见表1，各用水部门用水效益系数与用水成本系数见表2[31]。

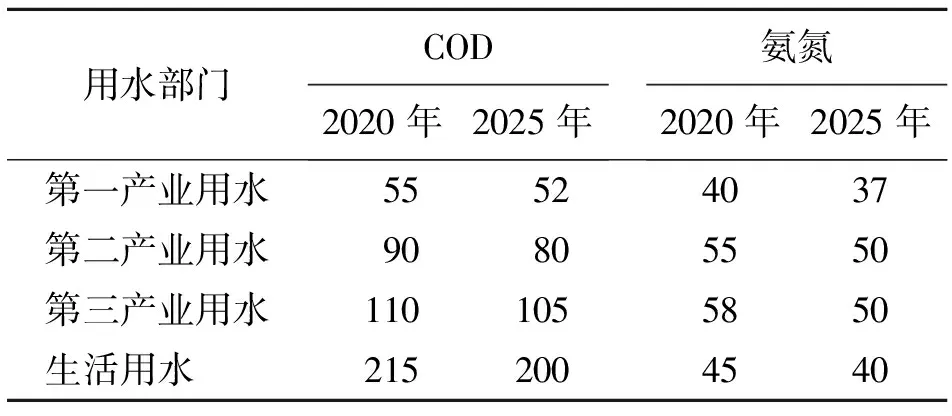
表1 规划期2020和2025年各用水部门用水污染物浓度 mg/L

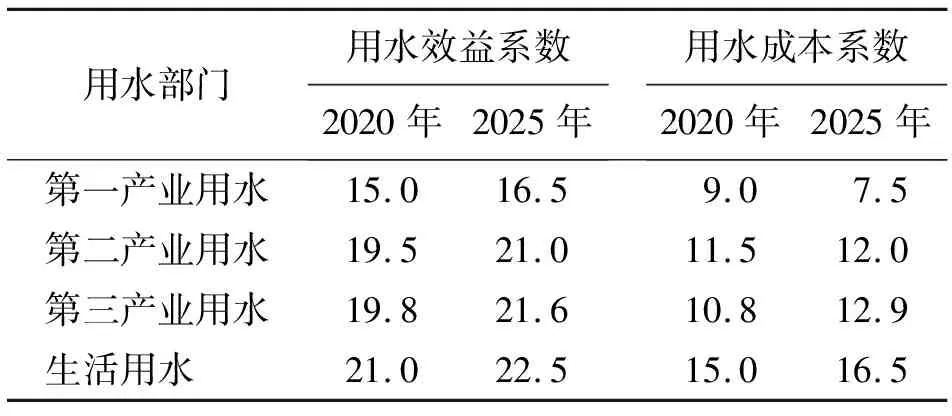
表2 规划期2020和2025年各用水部门用水效益系数与用水成本系数 元/m3

3.5 模型求解

多层规划模型的解法存在计算过程复杂、计算量大等问题。本文结合相互作用多阶段算法和Lingo18.0运算软件，针对武汉城市圈水资源配置模型建立基于模糊满意度的多阶段算法进行求解.具体求解步骤在此处不再赘述，详见文献[32]、[33]。

4 结果与分析

4.1 人均水足迹与水承载力分析

规划期2020和2025年武汉城市圈各城市人均水足迹见图5；2000-2015年武汉城市圈各城市人均水承载力见图6。分析图5可知，两个规划期内武汉城市圈的人均水足迹均值分别为0.95和1.01 hm2。其中武汉市和黄冈市水足迹均值较高，在两个规划期内均值分别达到了1.05和2.29 hm2，这是由于这两座城市在两个规划期内消耗了大量的生产及生活用水；天门市和鄂州市的水足迹相对较低，在两个规划期内的均值分别为0.62和0.64 hm2。分析图6可知，咸宁市2000-2015年平均人均水承载力在各城市中最高，其值为4.95 hm2，这是由于其控制水域面积较大，且经济活动水平较低。相比之下，武汉市、孝感市、天门市由于经济发展规模大、人口急剧增长，水承载力相对较小。考虑到水资源承载力与水足迹之比这一水资源承载指数，武汉城市圈水资源生态绩效总体上较佳，大部分城市水资源承载指数均大于1，尤其是咸宁市和黄石市，其人均水承载力指数分别达到了6.03和2.13，然而武汉市和孝感市等地也存在一定的水承载力不足。

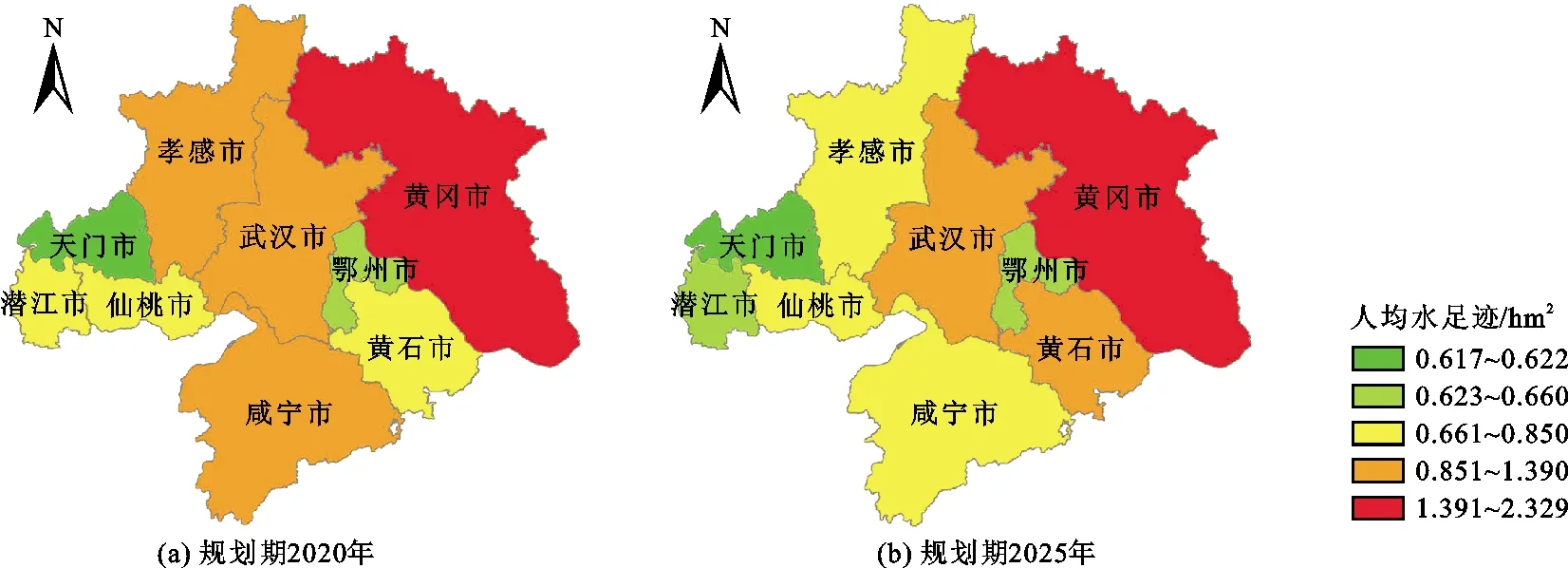
图5 规划期2020和2025年武汉城市圈各城市人均水足迹

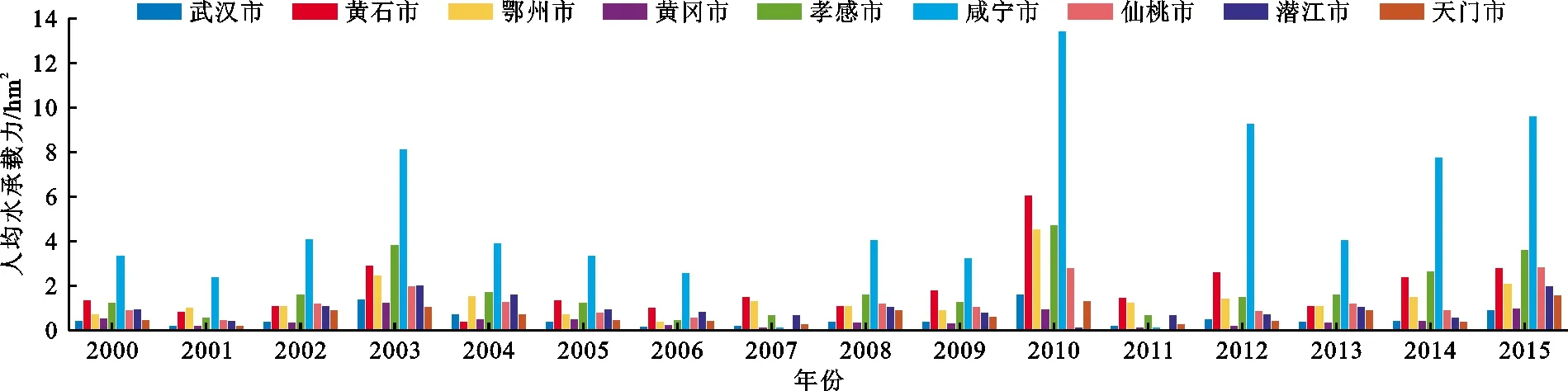
图6 2000-2015年武汉城市圈各城市人均水承载力

4.2 NLP-BES模型水资源配置分析

图7展示了规划期2020和2025年武汉城市圈的最佳水资源配置方案。在两个规划期内，区域配水总量分别达到209.83×108和229.48×108m3。分析图7中产业配水结果可知，该区域第一产业、第二产业、第三产业和生活用水在两个规划期的供水总量分别为261.57×108、107.70×108、37.30×108和32.74×108m3。分别占到总配水量的59.5%、24.5%、8.5%和7.5%；大部分生产用水用于第一产业，特别是黄冈市和孝感市，该两个城市第一产业供水量占武汉城市圈第一产业总供水量的50.45%；武汉市除第一产业之外，产业供水量均远大于其他城市，特别是第二产业与第三产业，其供水分别占城市圈第二产业与第三产业总供水量的54.6%与64.8%。就供水率而言，绝大部分城市的供水率达到了85%以上，孝感市供水率达到100%，潜江市和咸宁市供水率最低，分别为81.71%和82.56%(2025年)。从不同部门来看，缺水产业集中在第三产业与居民生活用水，其供水率分别为86.36%与85.71%。第一产业供水率最高，在两个规划期内达到了96.82%。

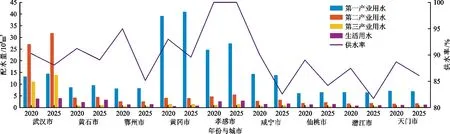
图7 规划期2020和2025年武汉城市圈水资源配置结果

4.3 NLP-BES经济效益和环境效益分析

规划期内武汉城市圈不同城市各产业的经济收益和污染物排放量如图8所示。由图8可知，两个规划期内系统总收益分别达到149.71×108和213.97×108元，相应的污染物排放总量分别为19.15×104和9.63×104t。武汉市的经济收益主要来源于第二产业与第三产业，而其余城市的经济收益中第一产业占比最高(图8(a))。从污染物排放来看，在第一个规划期(2020年)内，第二产业与居民生活的污染物排放总量达13.38×104t，占据了总污染物排放量的69.89%；在第二个规划期(2025年)内，居民生活污染物排放量减少至1.47×104t，占总污染物排放量的15.2%，第二产业污染物排放仍然为主要污染来源，占总污染物排放量的44.81%。从城市分布来看，武汉市在两个规划期内的污染物排放量分别达到7.86×104和4.25×104t，约占总污染物排放量的41.05%和44.10%，除第一产业外，武汉市各产业污染物排放量均显著超过其余8个城市的污染物排放量(图8(b))。

图8 规划期2020和2025年武汉城市圈不同城市各产业的经济收益和污染物排放量

4.4 各产业需水量敏感性分析

模型中涉及的各参数对决策结果有着重要影响，因此，有必要开展敏感性分析以确定参数的变化对模型结果的影响程度。本文重点研究各产业水资源需求的变化对系统收益及污染物排放量的影响，以规划期2020年为基准，分别对各城市不同产业需水量进行敏感性分析，分析结果如图9所示。由图9可见，较低的需水量将会产生较少的污染物排放量，同时也降低了系统收益。通过对各产业的需水量进行单一敏感性分析，结果表明第一产业需水量变化对经济效益最为敏感，平均每增加1%的用水量，可增加0.82×108元的收益(图9(a))。生活需水量与第二产业需水量变化对污染物排放控制最为敏感，平均每减少1%的用水量可分别减少682.54和671.92 t的污染物排放量(图9(b))。当同时对各个产业实施强节水与弱节水政策时，在[0.85,1.15]倍比区间内平均每增加1%的用水量可增加1.34×108元的经济效益，同时会增加0.19×104t的污染物排放量。

图9 武汉城市圈各产业需水量敏感性分析(规划期2020年)

4.5 不同水资源规划模型的优化结果对比与分析

分别以上层、中层和下层目标为目标函数，建立了3个传统的单目标优化模型，即以系统经济效益最大为主要目标的水资源规划模型(LP-MB)、以污染物排放量最小为主要目标的水资源规划模型(LP-ME)和以系统收益公平性为主要目标的水资源规划模型(LP-MS)。将规划期2020和2025年3个传统的单目标模型与3层规划模型(NLP-BES)的优化结果进行对比，结果如表3所示，由表3可看出，LP-MB模型仅从经济效益角度出发，其结果会得到最高的经济收益与污染物排放量，以及最大的不公平系数；LP-ME模型仅从环境效益出发，所以其优化结果的污染物排放量为最低，其经济收益也是3个单目标模型中最低的；LP-MS模型仅从各个城市所获经济效益的公平性出发，其所得优化结果的不公平系数为最低，污染物排放量及收益位于3个单目标规划模型的中间位置；NLP-BES模型综合考虑了环境因素、经济因素与社会稳定因素要求，其优化结果可以为各级决策者提供更加合理的水资源配置方案。总体而言，LP-MB的优化方案适用于力求区域经济高速发展的情景；LP-ME的优化方案体现了保护水源和改善水质的要求；LP-MS的优化方案适用于保持区域内公平发展的情景。而当同时兼顾经济效益、污染物排放与社会稳定因素时，NLP-BES的优化结果是一种切实的方案。

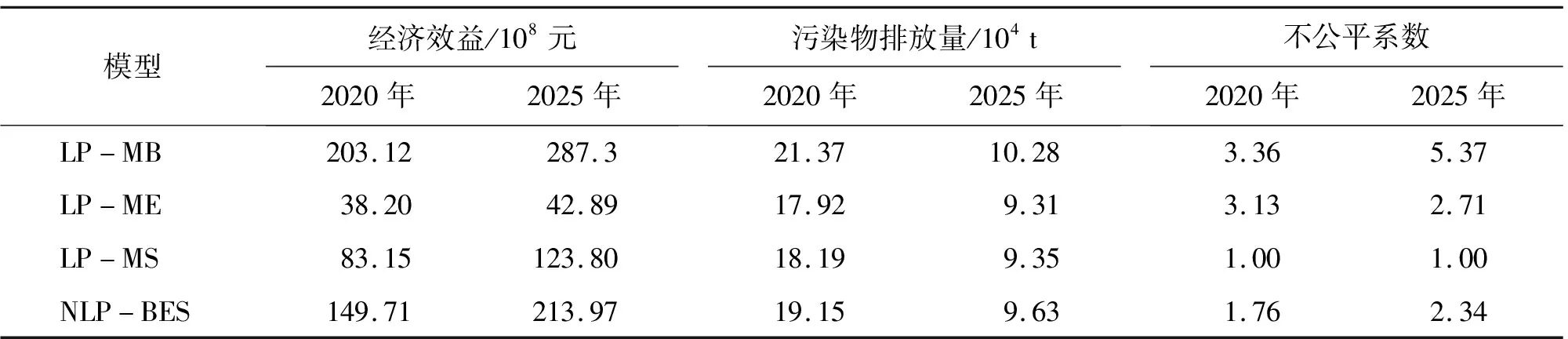
表3 规划期2020和2025年4种水资源规划模型优化结果对比

5 结 论

(1)NLP-BES模型能够反映复杂系统的多目标、多层次和多决策者的特征和交互影响，本文将其应用于武汉城市圈的水资源管理系统。该模型不仅解决了单目标模型的指向性过强的问题，也提高了双层模型在处理复杂领导-跟随关系的能力。

(2)结合交互式算法和模糊满意度算法，利用Lingo运算软件对NLP-BES模型进行求解，可以得到经济效益、污染物排放、不公平系数和系统满意度λ的优化结果。结果表明，武汉城市圈水资源生态状况总体良好，特别是咸宁市和黄石市，但武汉市、孝感市等城市也存在一定的水足迹赤字。2020和2025年两个规划期内系统总收益达363.68 ×108元，COD及氨氮排放量为28.78×104t。λ为权衡收益均等化、经济总效益和污染物排放量的重要因子，其值在两个规划期内分别为0.676与0.693。

(3)通过不同的水资源需求量敏感性分析，表明不同水资源需求约束对武汉城市圈水资源管理系统的经济效益与污染排放具有重要的影响。

(4)与各个单目标规划模型的优化结果对比分析表明，由于本文所采用的多层规划模型综合考虑了环境目标、经济目标与社会目标，从而有效规避了单目标规划模型偏向性过强等不足，其优化配置方案更加可行。