TD生成的三角模
2021-04-23孙文璟
孙文璟,李 琪,李 钢
齐鲁工业大学(山东省科学院) 数学与统计学院,济南 250353
三角模、三角余模作为典型的聚合算子,在多个领域取得了广泛应用[1-4]。例如,王国俊[1]利用三角模和三角余模构造推理空间的蕴涵算子;徐小湛等[2]利用阿基米德三角模的加法生成子和乘法生成子刻画模糊偏好理论中模糊关系的若干性质;王洪凯[3]基于三角模构造评判模型。因此我们构造充分多的三角模、三角余模十分必要,一些学者已经研究了不同的构造方法[5-8]。例如,李成允等[6]利用二元函数构造三角模;杜院录[7]借助一元单调减函数及其逆构造三角模。特别地,文献[9]至文献[11]利用一元函数及其伪逆构造不同的三角模。本文沿着文献[9]的思路,继续研究利用一元函数及其伪逆构造三角模。
主要工作及结构安排:第一部分给出本文研究过程中需要的一些基本知识;第二部分利用TD、一元函数及其伪逆构造三角模的相关结论,并给出相应对偶结论;第三部分对本文工作做出总结。
1 预备知识
文章中的一些基本概念和相关的部分结论:
定义1[12]:二元函数T:[0,1]2→[0,1],如果对∀x,y,z∈[0,1]满足以下四个条件:
T(x,y)=T(y,x)
(T1)
T(x,T(y,z))=T(T(x,y),z)
(T2)
T(x,y)≤T(x,z)y≤z
(T3)
T(x,1)=x
(T4)
则称T为三角模,其中,1称为T的单位元。
定义2[9]:一元非递减函数φ:[0,1]→[0,1],函数φ(-1):[0,1]→[0,1]:
φ(-1)(x)=sup{z∈[0,1];φ(z) (1) 称为φ的伪逆,约定supφ=0。 φ(-1)具有以下性质: 1)φ(-1)°φ(x)≤x,x∈[0,1]; 2)当φ严格递增时,φ(-1)°φ(x)=x,x∈[0,1]。 文献[9]中利用一元非递减函数及伪逆构造了特殊的三角模。 命题1[9]:一元非递减函数φ:[0,1]→[0,1],在开单位区间]0,1[上连续,T为三角模。则Tφ: (2) 是三角模。 由于极端积 是最小的三角模,表达式简单且在模糊逻辑中有重要应用[13-14],文献[9]中有如下结论: 命题2:设一元非递减函数φ:[0,1]→[0,1],二元函数(TD)φ:[0,1]2→[0,1]定义为 (3) 则(TD)φ=TD当且仅当φ(-1)(1)=1或φ(-1)(1)=0。 根据命题2,对于φ(-1)(1)∈]0,1[的情况,(TD)φ是否为三角模是一个值得深入研究的问题。 本节专注研究φ(-1)(1)∈]0,1[的情况下,(TD)φ是否为三角模。分两种情况讨论:1)φ(c)<1;2)φ(c)=1,其中c=inf{x|φ(x)=1}。另外,本节最后给出TD的对偶结论。 首先,我们给出几个例子。 例1:1)一元函数φ1:[0,1]→[0,1]定义为 2)一元函数φ2:[0,1]→[0,1]定义为 3)一元函数φ3:[0,1]→[0,1]定义为 注1:根据以上例子可知文献[9]中的定理1:设一元非递减函数φ:[0,1]→[0,1],则(TD)φ是三角模,且(TD)φ(x,y)= (4) 存在错误。例如以上例子中的(TD)φ均不是三角模且表达式与(4)不吻合。 根据例1得出以下结论: 命题3:设一元非递减函数φ:[0,1]→[0,1]满足φ(c)<1,其中c=inf{x|φ(x)=1}。则(TD)φ是三角模,当且仅当 (TD)φ(x,y)= (5) 其中,b=inf{x|φ(x)=φ(c)}。 证明:(必要性)设(TD)φ是三角模,证明(TD)φ具有表达式(5)。 我们可知函数φ满足下列性质: 1)不存在区间]x0,x1[⊂]0,c[使得函数φ严格递增; 2)函数φ至多存在两个区间]m1,n1[,]m2,n2[⊂[0,c]使得φ(x)=c1,∀x∈]m1,n1[,φ(y)=c2,∀y∈]m2,n2[,c1≠c2; 3)函数φ(x)在x=b处左连续。 且函数φ具有如下表达式 (6) 其中,M,N∈[0,1],M≤N。 下面给出相应证明。 假设函数φ在]x0,x1[⊂]0,c[上严格递增,取x2∈]x0,x1[,x3∈]c,1],有 (TD)φ(x3,(TD)φ(x2,x3))=x2; (TD)φ(x2,(TD)φ(x3,x3))=0。 所以(TD)φ不具有结合性,不是三角模。 假设函数φ存在三个区间]m1,n1[, ]m2,n2[,]m3,n3[⊂[0,c]使得φ(x)=c1,∀x∈]m1,n1[,φ(y)=c2,∀y∈]m2,n2[,φ(z)=c3,∀z∈]m3,n3[,c1 假设函数φ在b点不是左连续的,取x2∈[0,b[,x3∈]c,1],有 (TD)φ(x3,(TD)φ(x2,x3))=b≠0=(TD)φ(x2,(TD)φ(x3,x3)),所以(TD)φ不具有结合性,不是三角模。 由此可知,φ满足上述性质且具有表达式(6)。 经过计算可知 (7) 且(TD)φ具有表达式(5)。 (充分性)容易看出(TD)φ满足交换性、单调性且具有单位元1。下证(TD)φ具有结合性,即对∀x,y,z∈[0,1]下面等式成立 (TD)φ((TD)φ(x,y),z)=(TD)φ(x,(TD)φ(y,z))。 不失一般性,设x≤y≤z。 1)x∈]b,c],y∈]c,1[,z=1 (TD)φ((TD)φ(x,y),z)=b=(TD)φ(x,(TD)φ(y,z)); 2)x,y,z∈]c,1[ (TD)φ((TD)φ(x,y),z)=b=(TD)φ(x,(TD)φ(y,z)); 3)x,y∈]c,1[,z=1 (TD)φ((TD)φ(x,y),z)=c=(TD)φ(x,(TD)φ(y,z)); 4)y=1 (TD)φ((TD)φ(x,y),z)=1=(TD)φ(x,(TD)φ(y,z)); 5)x,y,z的其它取值,有 (TD)φ((TD)φ(x,y),z)=0=(TD)φ(x,(TD)φ(y,z))。 所以,(TD)φ具有结合性,是三角模。 例2:1)一元函数φ4:[0,1]→[0,1]定义为 则根据式(1)(3)得 (TD)φ4(x,y)= 2)(例3中的φ6)一元函数φ5:[0,1]→[0,1]定义为[8] 根据命题3结论知(TD)φ应具有如下正确形式: (TD)φ5(x,y)= 围绕φ(c)=1的情况,文献[8]给出了如下结论: (TD)φ(x,y)= (8) 例3:一元函数φ6:[0,1]→[0,1]定义为 (TD)φ6(x,y)= 例3中φ6不满足命题4的条件,仍是三角模。下面给出命题4的推广结论。 (TD)φ(x,y)= (9) 证明:首先证明(TD)φ具有表达式(9)。 1)(x,y)∈[0,c[2 φ(x)<1,φ(y)<1,TD(φ(x),φ(y))=0,由此可得(TD)φ(x,y)=0; 2)(x,y)∈[c,1[2 φ(x)=φ(y)=1,TD(φ(x),φ(y))=1,由此可得(TD)φ(x,y)=φ(-1)(1)=c; 3)(x,y)∈[c,1[×[ai,bi[ φ(x)=1,φ(y)=ci,TD(φ(x),φ(y))=ci,由此可得(TD)φ(x,y)=φ(-1)(ci)=ai; 4)(x,y)∈[ai,bi[×[c,1[ 根据(TD)φ的交换性和上述3)可知,(TD)φ(x,y)=ai; φ(x)=1,TD(φ(x),φ(y))=φ(y),由此可得(TD)φ(x,y)=φ(-1)(φ(y))=y=TD(x,y); 根据(TD)φ的交换性和上述5)可知,(TD)φ(x,y)=x=TD(x,y)。 所以,结论成立。 下面证明(TD)φ是三角模。容易看出(TD)φ满足交换性、单调性且具有单位元1。下证(TD)φ具有结合性,即对∀x,y,z∈[0,1]下面等式成立 (TD)φ((TD)φ(x,y),z)=(TD)φ(x,(TD)φ(y,z))。 不失一般性,设x≤y≤z。 1)x∈[ai,bi[,y,z∈[c,1[ (TD)φ((TD)φ(x,y),z)=ai=(TD)φ(x,(TD)φ(y,z)) (TD)φ((TD)φ(x,y),z)=x=(TD)φ(x,(TD)φ(y,z)); 3)x,y,z∈[c,1[ (TD)φ((TD)φ(x,y),z)=c=(TD)φ(x,(TD)φ(y,z); 4)z=1 (TD)φ((TD)φ(x,y),z)=(TD)φ(x,(TD)φ(y,z)); 5)x,y,z的其它取值,有 (TD)φ((TD)φ(x,y),z)=0=(TD)φ(x,(TD)φ(y,z))。 所以,(TD)φ具有结合性,是三角模。 例4:设一元函数φ7:[0,1]→[0,1]定义为 则根据公式(1)(3)得 (TD)φ7(x,y)= 我们发现,φ7不满足命题5的条件,但(TD)φ7仍具有表达式(9)。因此,命题5中的条件是充分但非必要的。 我们可知 与TD是对偶的,根据3.1和3.2节所得结论,我们可以得出以下对偶结论: 命题6:设一元非递减函数φ:[0,1]→[0,1],二元函数(SD)φ:[0,1]2→[0,1]定义为 (SD)φ(x,y)= (10) 则(SD)φ=SD当且仅当φ[-1](0)=1或φ[-1](0)=0,其中,φ[-1](x)=inf{z∈[0,1];φ(z)>x},约定infφ=1。 命题7:设一元非递减函数φ:[0,1]→[0,1]满足φ(c)>0,其中b=sup{x|φ(x)=0}。则(SD)φ是三角余模,当且仅当(SD)φ具有如下表达式 (SD)φ(x,y)= (11) 其中,c=sup{x|φ(x)=φ(b)}。 (SD)φ(x,y)= (12) 本文讨论了由TD三角模出发构建新三角模的方法,通过单位区间[0,1]上的一元非递减函数φ进行变换,对(TD)φ进行了完整的刻画,同时给出TD的对偶三角余模SD的对偶结论。2 主要结论
2.1 情形1:φ(c)<1
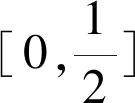

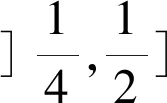
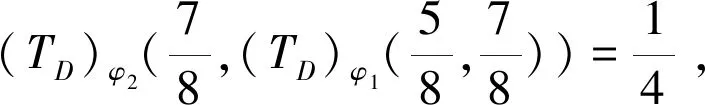
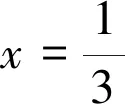

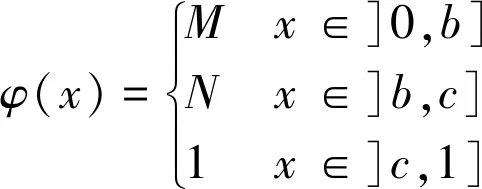
2.2 情形2:φ(c)=1
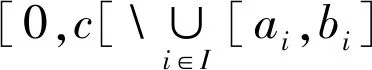


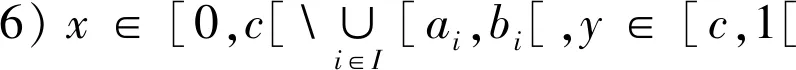
2.3 对偶结论

3 总 结
