岩溶沉陷区埋地管道预警与极限位移响应分析

李 霖， 兰才富， 李 虎

(1.国家管网集团公司西南管道南宁输油气分公司， 南宁 530022； 2.西南石油大学 石油与天然气工程学院，成都 610500； 3.四川省地质工程勘察院集团有限公司， 成都 610072)

在长输油气管道快速建设过程中会穿越众多地质灾害区域，其中也不可避免地穿越岩溶沉陷区[1]。据统计中国可溶岩分布面积约达到国土面积的1/3以上，是世界上岩溶最发育的国家之一，其中四川、云南、广西等地分布最为广泛[2]。喀斯特岩溶是易溶岩，主要隐藏在地下，由于其地下水发育，水溶性溶解岩石在水的作用下发生溶蚀现象，造成一定区域的空洞，在相应的环境作用或外部荷载作用下造成上部岩土体发生沉降或坍塌，从而对埋地长输油气管道造成严重破坏，危机附近居民和环境[3-4]。

国外对喀斯特岩溶地区的研究始于19世纪末[5]，主要以对喀斯特地貌的评价为主。Magdalene等[6]和Gao等[7]运用G1S技术对地质条件、覆土厚度、地表水系等一系列因素进行了量化分析并以此建立了相应的评价模型。Zisman[8]运用SPT参数且将地质特征作为岩溶塌陷区危险评价因子，对佛罗里达州岩溶区进行了评价。Katarina等[9]运用加权回归法、K-Function法等统计算法在空间上分析了人为因素和自然因素对岩溶塌陷区的影响。国内学者针对塌陷区长输油气管道的研究主要为解析法和数值分析法。高惠瑛、冯启民[10-11]在研究塌陷区使管道几何大变形的基础上将轴力与弯矩作用考虑到管道塑性状态下，建立了塌陷区管道失效判据。张鹏等[12]在分析管道不同角度穿越沉陷区时得到了管道最大应力的时变性规律以及管道最大应力位置。游东潘[13]运用ABAQUS有限元软件对岩溶塌陷区管道的力学行为做了分析，提出了穿越岩溶地区管道建设的相关建议。王惠[14]运用数值模拟分析方法对沉陷盆地的输油管道力学行为进行分析得出了相应因素的敏感性顺序。以上研究均未直接指出油气管道在不同岩溶沉降长度下管道的最大位移和相应状态下的应力分布状态，也未指出岩溶地区塌陷后最大悬空长度和在一定沉陷长度下管道的预警位移。且对于长输油气管道穿越岩溶地带时，由于不同的输送内压可能会使得不同长度沉降下管道的最大位移不同。在一定沉降长度下，管道是否达到管道允许的最大位移将是初步判断管道安全性的重要参数，且按90%屈服应力所对应的预警位移可作为管道安全运营的预警参数，保证管道安全。因此，研究岩溶地区不同内压下管道最大位移和预警位移以及管道最大悬空长度对管道安全运行具有重要作用。

针对以上问题，以西南某穿越岩溶地区埋地输气管道为例，运用ABAQUS有限元软件建立管-土三维模型，分析岩溶地区在不同输送内压时不同沉陷长度下管道的最大位移和管道预警位移，得到其最危险位置，且考虑悬空状态下管道最大悬空长度，以期为穿越岩溶地区管道的安全评价和及时治理提供参考。

1 穿越岩溶地区埋地管道变形特征

岩溶地区由于地下水的影响形成土洞，土洞上部土体沉陷使管道发生弯曲，甚至发生破坏，此时管道受到自身重力之外还受到上部土体重力影响。根据现有文献对岩溶塌陷区管道力学行为的影响，将管道看作是受均布荷载的Winkler地基梁模型[15-16]，在此模型基础上计算得到管道位移为

y=

(1)

式中：参数λ与弯矩M的表达式为

(2)

(3)

式中：y为管道挠度,m;W为管道最大沉降值,m;M为管道沉降边缘点弯矩,N·m;l为最大沉降点到边缘点的距离,m;EI为管道的弯曲刚度;x为管道上一点到沉降边缘点的距离,m;k为弹性地基系数。

通过管道挠度方程和边界点弯矩可以得到受弯曲影响下管道上任意一点应力值，即

(4)

根据式(1)～式(4)可在一定精度上计算管道的力学响应。

2 岩溶沉陷区数值分析模型

2.1 有限元模型

本模型以西南某穿越岩溶地区输气管道为例，该线所用输送管道为X80管材，经勘探管道平均埋深2 m，外径1 016 mm，壁厚15.3 mm，设计运输内压为10 MPa，管材屈服应力为555 MPa。采用ABAQUS有限元软件进行模拟分析，土体采用摩尔-库仑模型，材料参数如表1所示，查阅文献[17]得到管道应力应变数据作为本次模拟的管道力学参数，如图1所示。计算模拟长度为10～100 m时管道不同内压下的最大位移状态和在管道发生悬空时不同内压下的极限悬空长度，将90%的屈服应力作为管道的预警应力[18]，分析预警应力时不同沉陷长度下管道的预警位移。

表1 材料参数

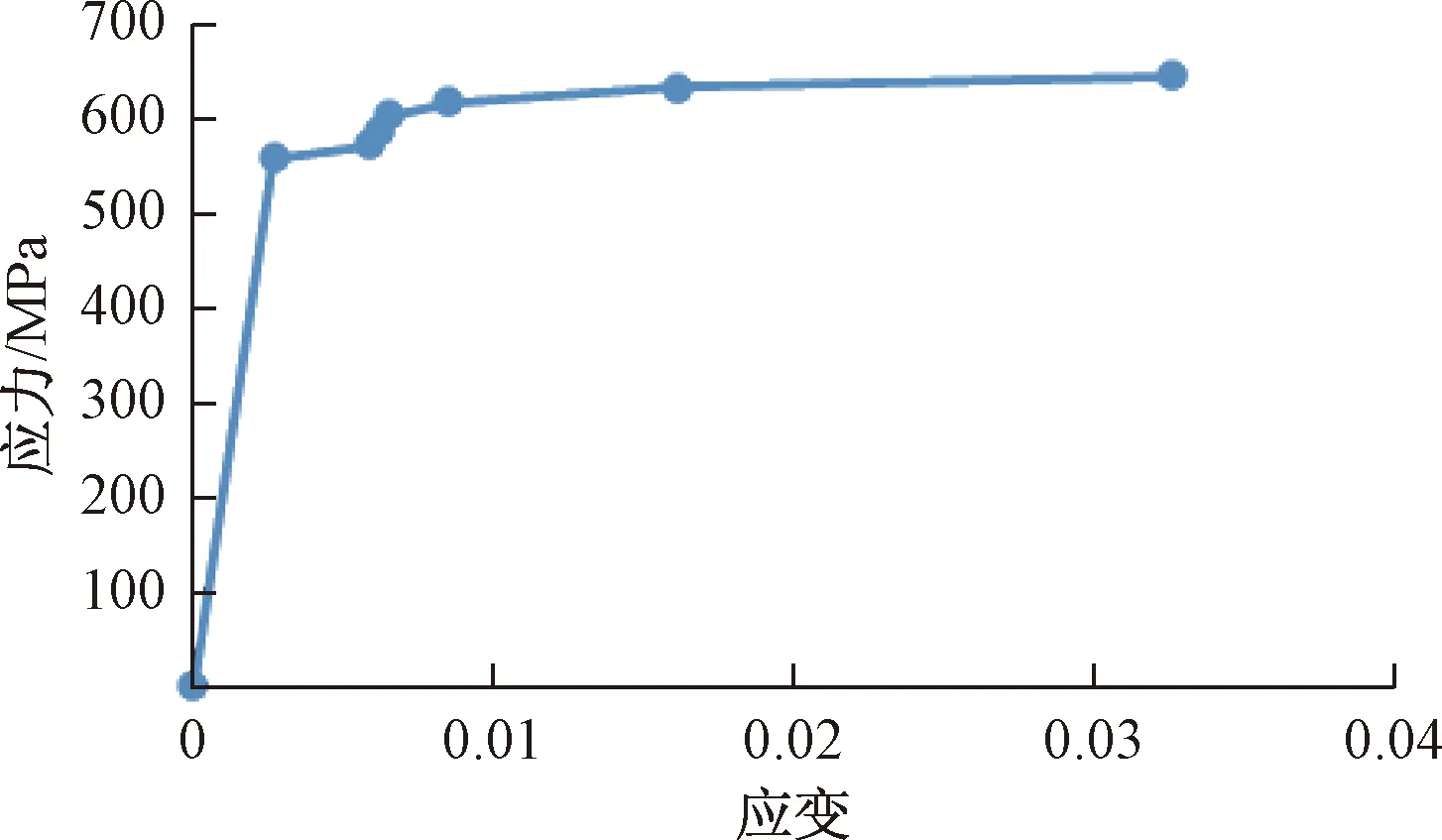
图1 x80管材应力-应变曲线

图2 岩溶沉陷模型

查阅相关资料，由于管道受影响的非沉陷区域长度是沉降区域长度的0.49倍[19]，且模拟沉陷区长度为10～100 m，故选取模型长度为200 m，土体横截面简化为5 m×5 m。将模型走向和横向部分分别施加对称约束，将模型底部未沉陷区域设置为固定约束，如图2所示。管-土之间采用罚函数约束其接触行为，管-土间摩擦系数取0.5。由于在外界荷载作用下短距离的沉陷区域仍然可能使得管道发生破坏，且岩溶沉降为漏斗式，故在沉降区域土体上施加二次抛物线位移函数以模拟在自然沉降或受外界荷载作用下管道达到极限位移，其函数为

(5)

式中：y为沉陷区各点位移值,m;x为沉陷区内一点到沉陷边缘的距离,m;c为沉陷下沉值,m;l为沉陷区长度,m。

2.2 模型验证

本次建模所采取的边界约束条件与文献[19]相似，故仅对模型的网格敏感性进行分析，以期能使模拟结果更加精确。以沉陷区域长度10 m为例，将非沉陷区网格尺寸取为2 m，沉陷区网格尺寸取2、1.5、1、0.5 m作为敏感性分析尺寸，划分网格总体数量分别为16 796、18 116、20 656、28 376个，分别施加最大位移为0.2 m的位移二次函数，结果如图3所示。

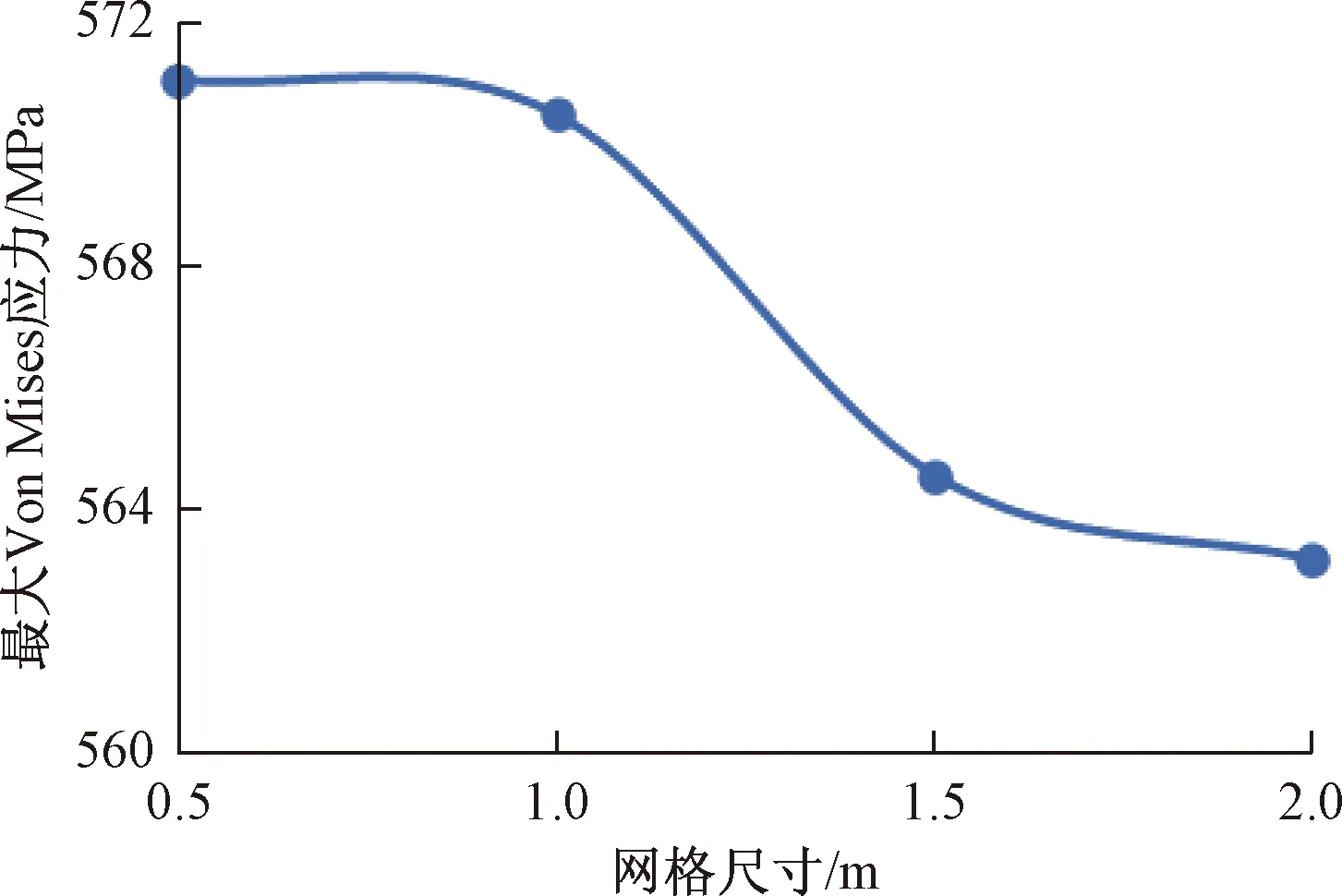
图3 模型网格验证

由图3可知，网格尺寸为0.5、1、1.5、2 m时管道最大应力分别为571.04、570.46、564.34、563.18 MPa，可知当网格尺寸小于1 m时，其管道最大应力相差极小，相对误差值在5%之内，认为结果可行可信，故取网格尺寸为1 m。

3 沉陷区管道响应分析

根据所建立的模型，由于需要计算到管道达到屈服的最大位移，故在沉陷区施加从0.2到1.2 m，增量为0.05 m的位移，分别计算无压、5 MPa、10 MPa时管道在不同沉降长度下达到管道屈服应力和预警应力时的力学响应分析，并得到管道屈服和预警时的最大位移和预警位移。

3.1 无压时管道响应分析

为分析管道在无压时受沉陷作用的力学行为变化，得到管道最大位移和预警位移以及最危险位置，由有限元计算得到沉降长度为10 m的土体位移云图如图4所示，管道位移云图如图5所示，各长度下管道达到屈服时应力如图6所示，管道最大位移如图7所示。其达到屈服时最大位移、管道预警位移及危险位置见表2。

图4 无压时沉降10 m土体位移云图

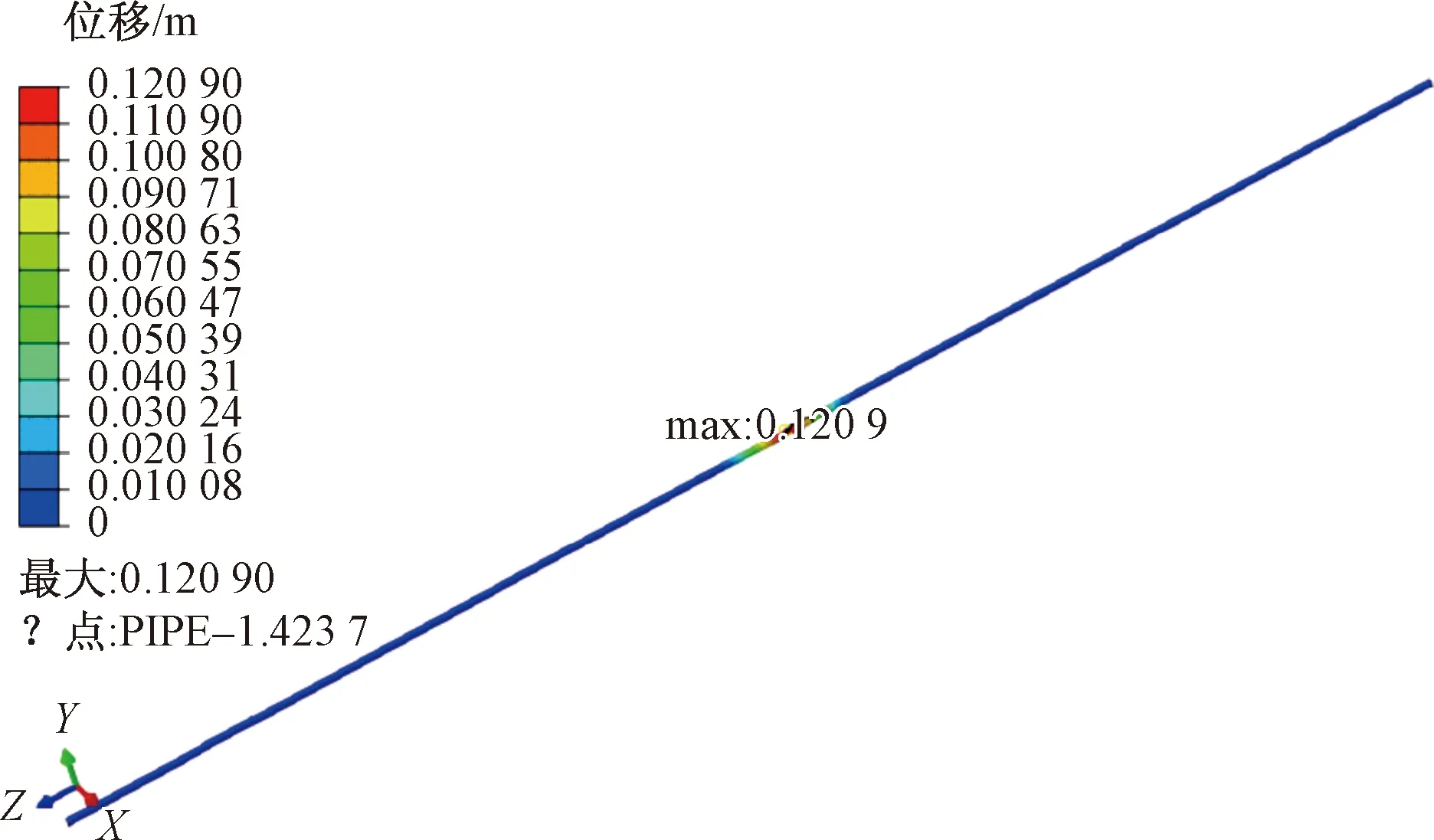
图5 无压时沉降10 m管道位移云图

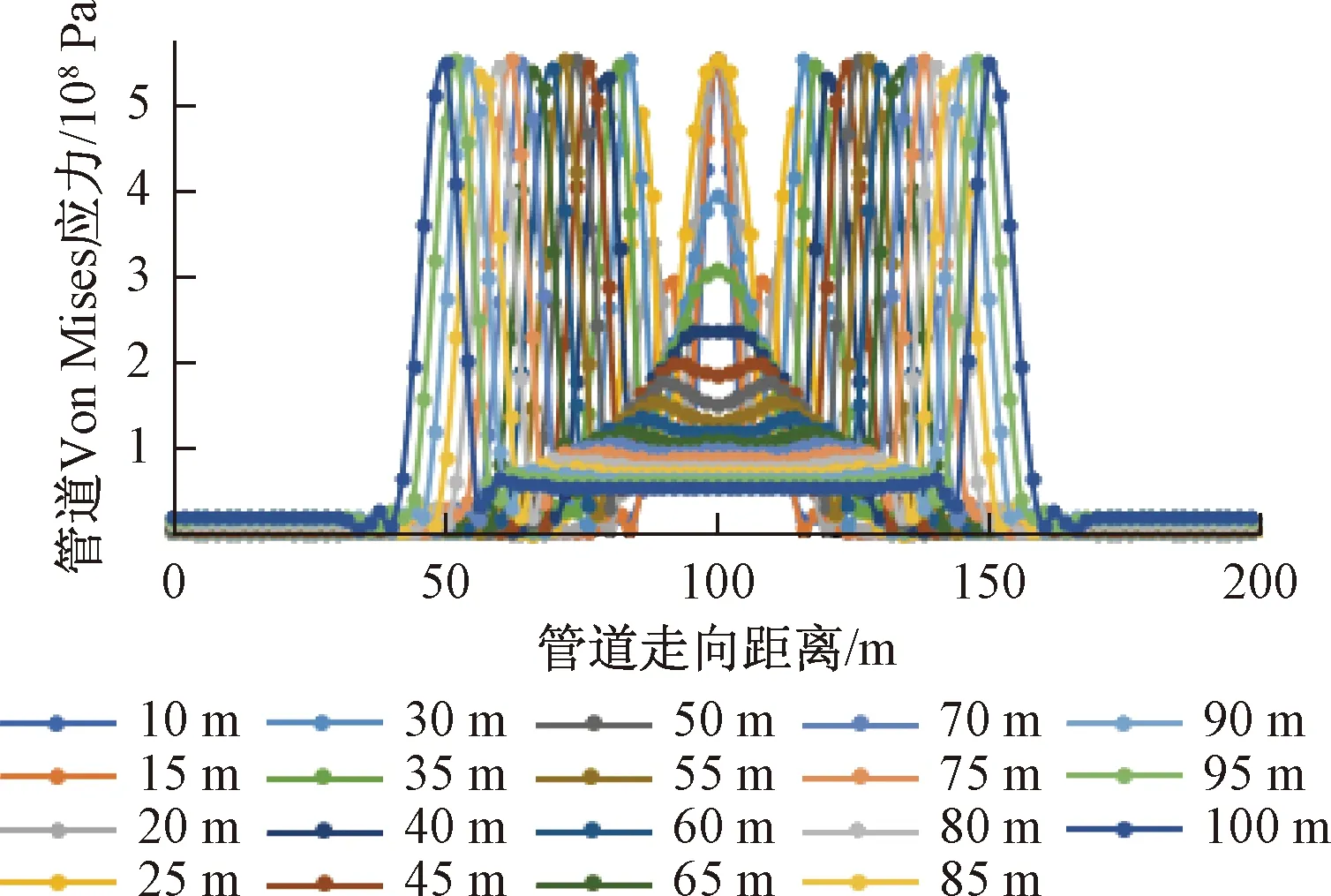
图6 无压时不同沉陷长度下管道应力曲线

图7 无压时不同沉陷长度下管道位移曲线

由图6可知，当沉降长度小于等于25 m时，管道在跨中位置达到屈服，此时两端最大应力为393.75 MPa，这是由于在短距离沉降时管道应力主要来自于受到沉降的弯曲作用，而在两端位置管道应力则随着沉降长度的增长而不断增加，两端受到的剪力作用不断加强。当沉降长度大于等于30 m时，管道则在两端位置率先达到屈服强度，沉陷长度30 m时跨中最大应力为395.86 MPa，管道主要收到两端土体位移的剪切作用，跨中位置管道应力则随着沉陷长度的增长而不断减小。

由图7可知，当管道达到屈服时，其最小极限位移为沉降长度10 m时达到112.05 mm，最大极限位移为沉降长度100 m时达到1 035.25 mm，且随着沉降长度的增加管道能承受的最大位移也在不断增加，且基本成线性增长。

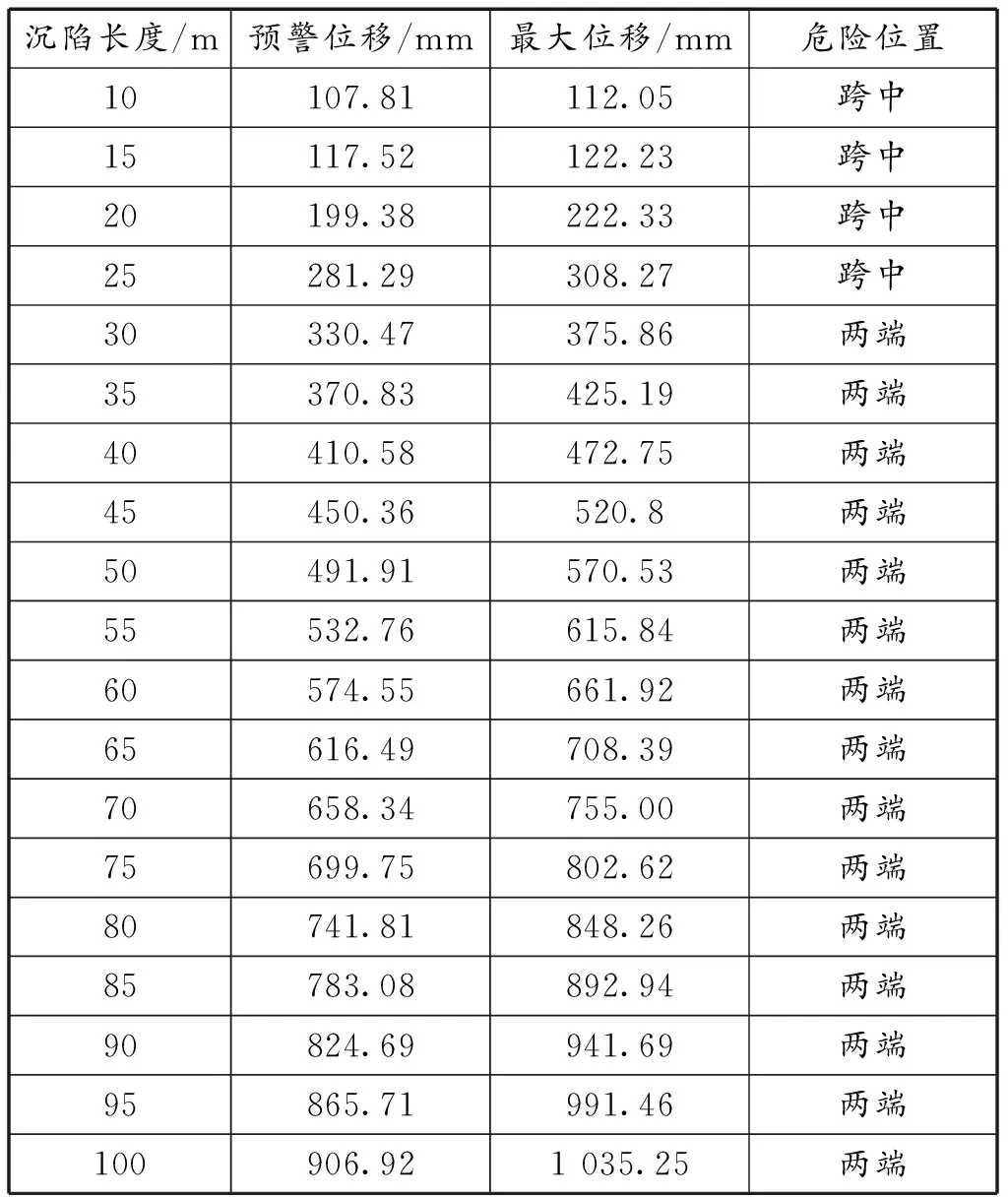
表2 无压时沉降管道危险位移

由表2可知，根据预警位移与最大位移对比，沉陷长度为10 m时两者相差较小，预警位移为107.81 mm，达到预警级别，差值仅有4.24 mm，随着长度的增加差值也逐渐增加，长度达到100 m时达到以预警级别的预警位移为906.92 mm，差值达到128.33 mm。

3.2 5 MPa内压下管道响应分析

在5 MPa的运输内压下管道的力学行为变化以及预警位移结果如下，不同长度下管道达到屈服时应力如图8所示，管道屈服时达到最大位移如图9所示。其达到屈服时最大位移、管道预警位移及危险位置见表3。

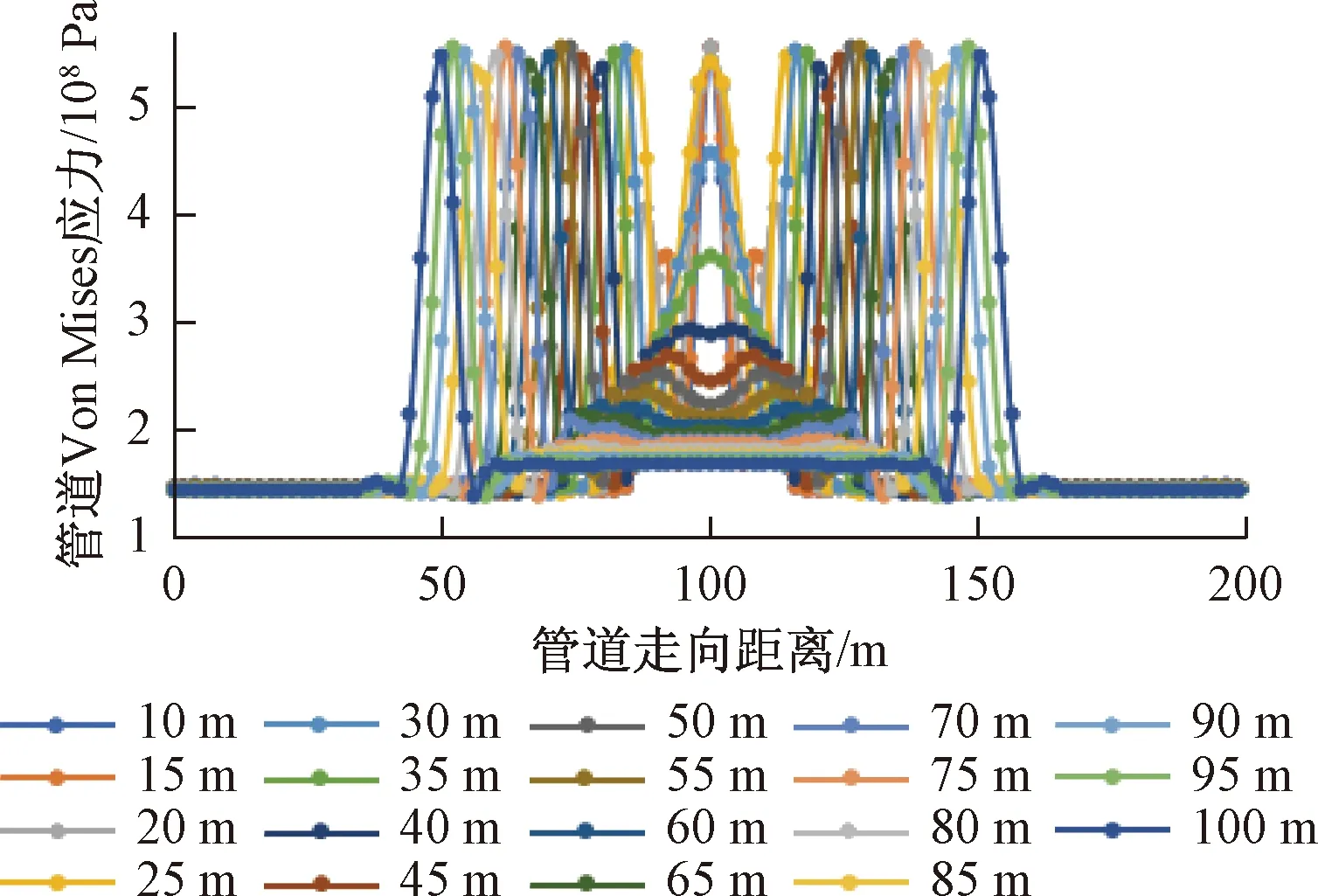
图8 5 MPa时不同沉陷长度下管道应力曲线

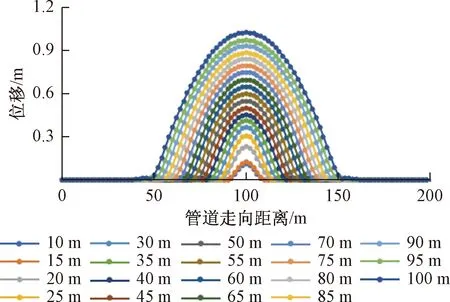
图9 5 MPa时不同沉陷长度下管道位移曲线

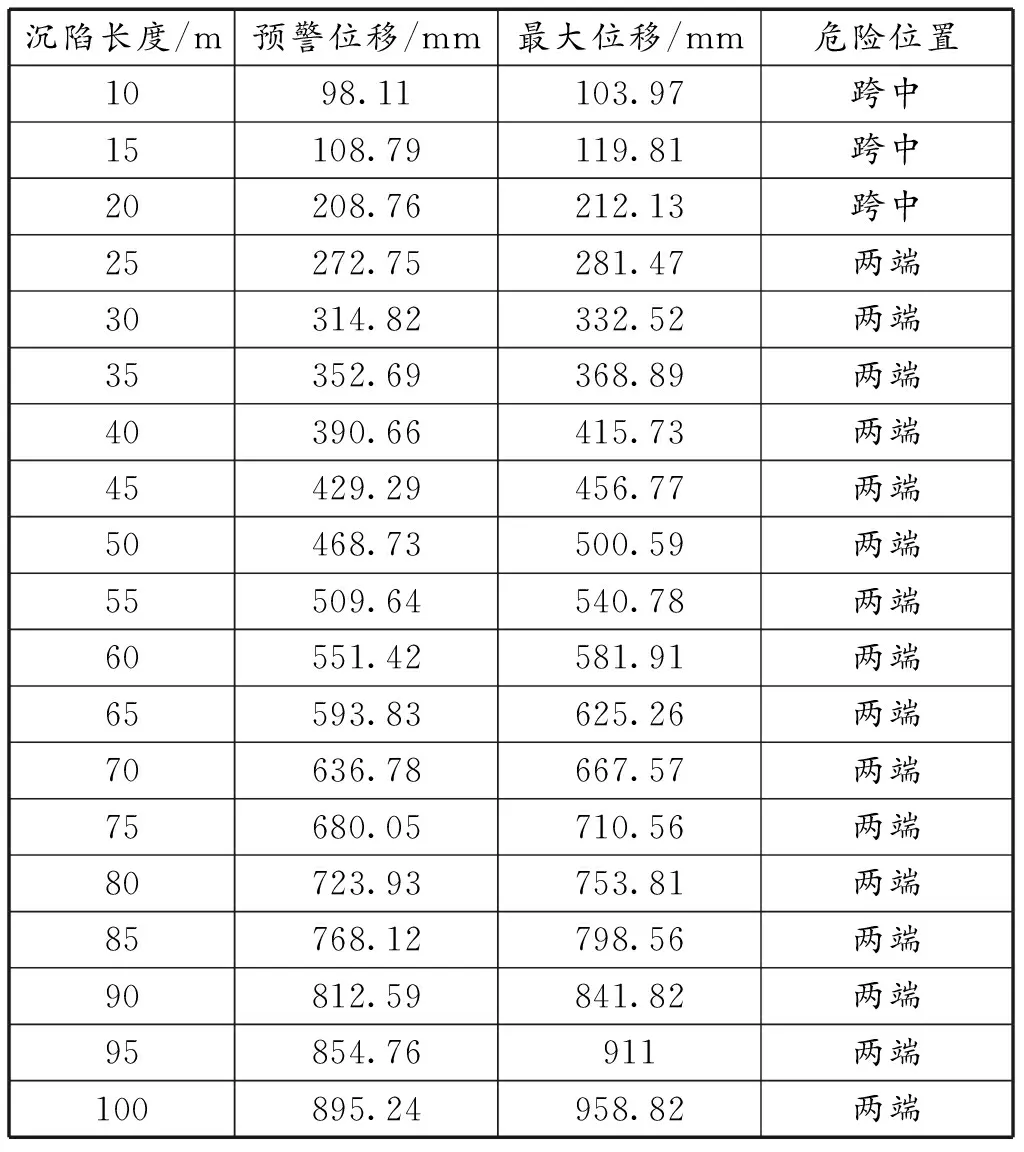
表3 5 MPa时沉陷管道危险位移

由图8可知，在5 MPa内压下管道沉陷长度小于等于20 m时，管道在沉陷段跨中率先达到555 MPa屈服强度，此时沉陷20 m时管道两端应力为405.42 MPa，管道沿线应力成山字形分布。当沉陷长度大于等于25 m时，管道则在两端位置达到屈服强度，沉陷25 m时管道跨中最大应力为458.54 MPa，且随着沉陷长度的增加其跨中位置最大应力逐渐减小。

由图9可知，管道沿线位移趋势与无压时管道位移趋势相同，其最小极限位移为沉陷长度10 m时达到103.97 mm，最大极限位移为沉陷长度100 m时达到958.82 mm。

由表3可知，管道沉陷长度在20 m以下时危险位置位移跨中，沉陷长度超过25 m则危险位置在两端，比无压时危险位置最早出现在两端的长度短，且预警位移与屈服位移均比无压时小，预警位移与最大位移之差随着沉陷长度的增大逐渐增大，最小为沉陷10 m时，预警位移为98.11 mm，相差5.86 mm。当沉陷长度为100 m时最大位移比无压时少76.5mm，减少了7.39%。

3.3 10 MPa内压下管道响应分析

在设计内压下管道的力学行为变化以及管道预警位移变化如下，不同长度下管道达到屈服时应力如图10所示，管道达到屈服时的位移如图11所示。其达到屈服时最大位移和预警位移及危险位置见表4。

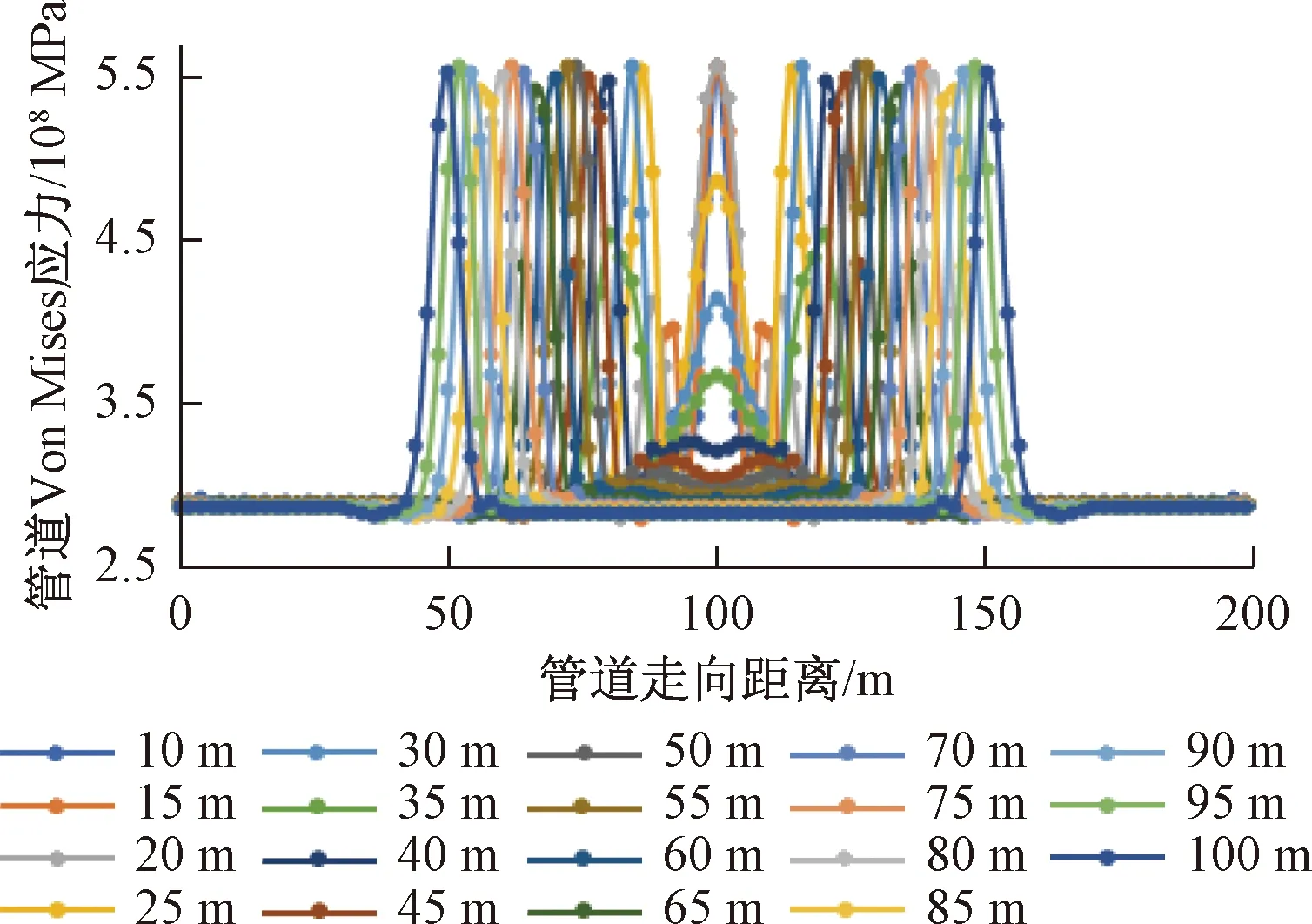
图10 10 MPa时不同沉陷长度下管道应力曲线

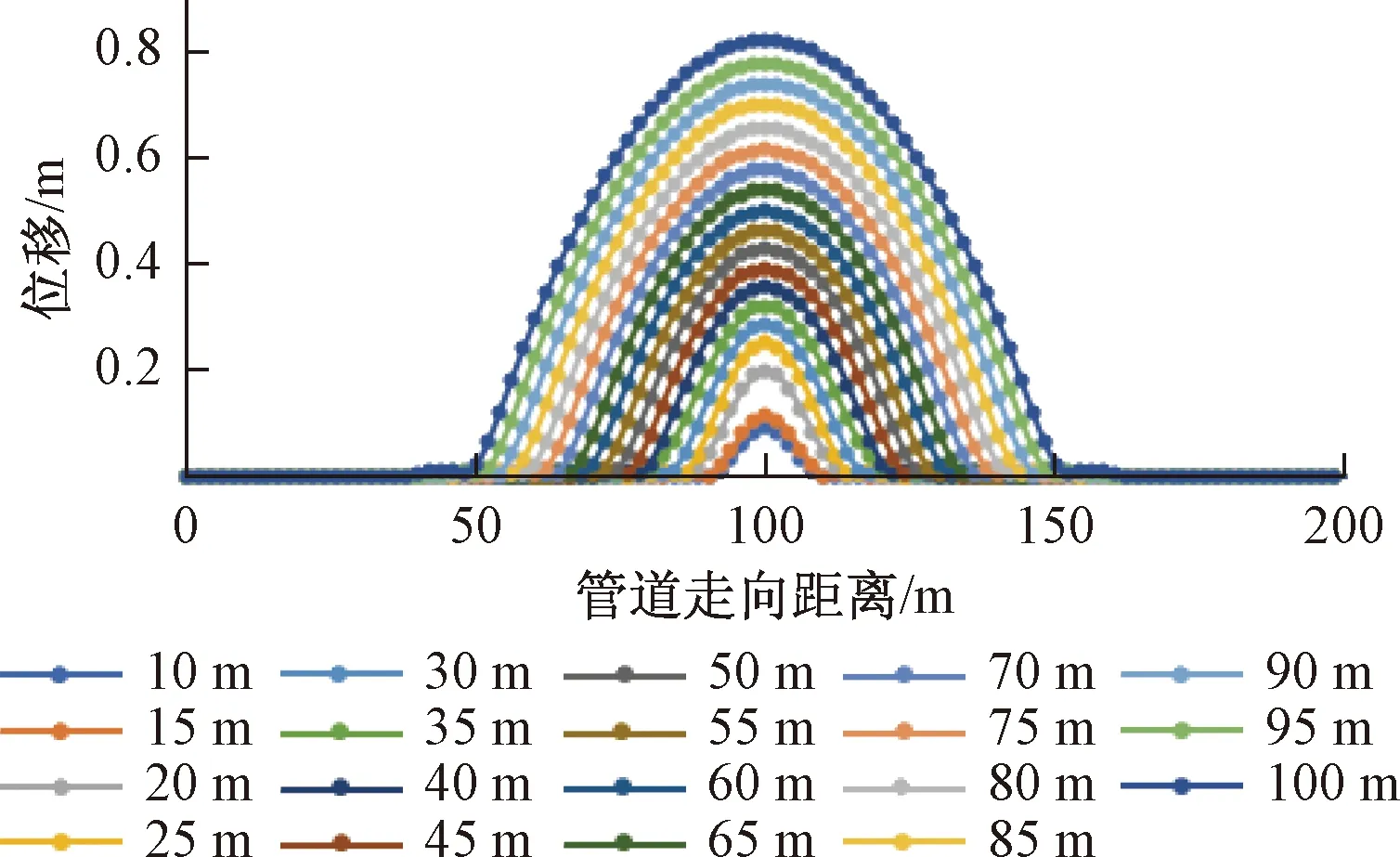
图11 10 MPa时不同沉陷长度下管道位移曲线

由图10可知，在10 MPa设计内压下沉陷长度小于等于15 m时，管道在沉陷段跨中位置率先达到屈服，此时管道跨端位置应力为394.95 MPa，管道沿线应力成山字形分布。当沉陷长度大于等于20 m时，管道则在两端位置达到屈服强度，此时沉陷25m时管道跨中位置应力为485.21 MPa，其应力变化趋势与无压和5 MPa工况相同。

由图11可知，管道沿线位移趋势与无压时管道位移趋势相同，其最小极限位移为沉陷长度10 m时达到95.99 mm，最大极限位移为沉陷长度100 m时达到826.78 mm。

表4 10 MPa时沉陷管道危险位移

由表4可知，管道沉陷100 m时预警位移为684.42 mm，与最大位移相差，危险位置在两端，沉陷长度小于15 m时危险位置位于跨中，超过20 m则危险位置位于两端处。对比表2、3、4可知，管道内压越大管道沉陷危险位移越小，且管道内压越大，危险位置出现在两端时的沉陷长度越短。故在发生溶岩沉陷时及时停输断气不仅可以防止泄露也可以加大管道的危险位移，在一定程度上防止管道发生二次危害，且根据90%屈服应力所得到的管道预警位移可在一定程度上为管道安全预警做出判断，提高管道安全性。

4 悬空时管道响应分析

管道在穿越岩溶地带时，若岩溶空洞发生突然性的塌陷，则使得管道会发生突发性悬空，管道在不同内压下最大的悬空长度则是对管道安全性进行初步判断的重要参数。因此，将分别计算不同内压下管道能达到的最大悬空长度，根据相关文献[20-21]建立相关的有限元模型，分析在悬空长度从50 m到600 m时管道的力学响应变化，不同悬空长度下管道最大应力-应变变化曲线如图12所示，最大位移变化曲线如图13所示。

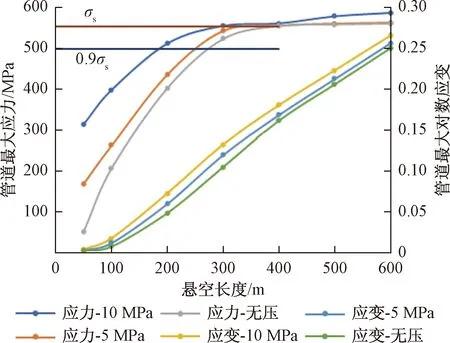
图12 管道最大应力-应变曲线

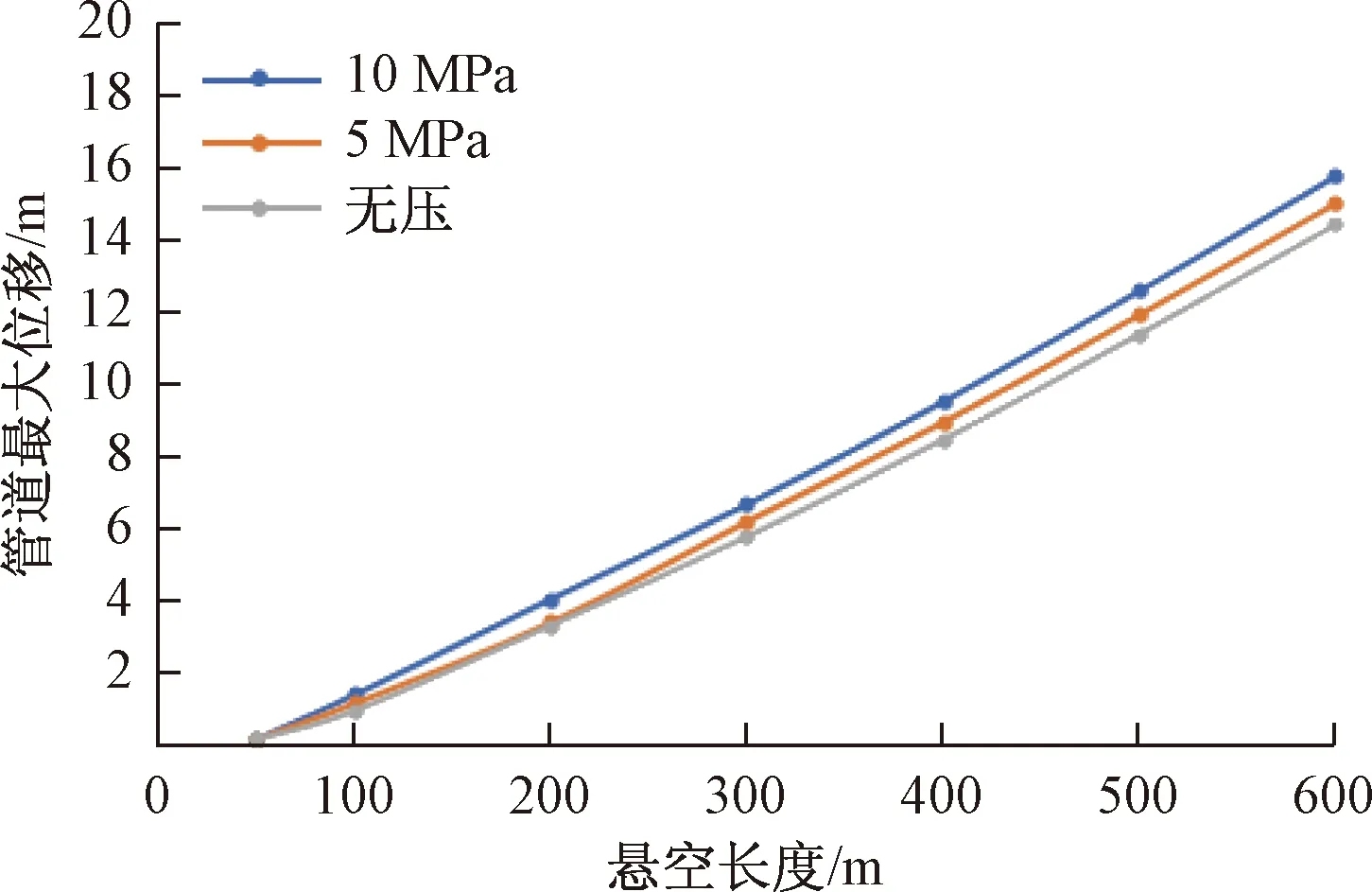
图13 管道最大位移曲线

由图12可知，管道在内压为10、5 MPa和无压状态下达到屈服时的最大悬空长度分别约为280、340、380 m，而按照0.9倍屈服极限的预警位移则最大悬空长度分别约为190、250、270 m，可知管道最大应力随着悬空长度的增加先迅速增加，达到屈服应力后开始区域平稳，而管道应变则随着悬空长度的增加而增加，且基本成线性增长趋势。由图13可知，管道在不同内压下最大位移随着悬空长度的增加差值逐渐增大，且随着悬空长度的增加管道最大位移成线性增长。

5 结论

通过有限元数值分析，分析了在不同内压下管道不同沉陷长度时的最大位移和预警位移以及不同内压下管道的最大悬空距离，得出以下结论：

1)当沉陷长度较小，管道跨中达到屈服时，随着沉陷长度的增加管道两端最大应力逐渐增加，当管道两端达到屈服时，管道跨中位置最大应力随着沉陷长度的增加而不断减小，且管道应力呈“山”字形分布。

2)管道内压越大，危险位置出现在两端时的沉陷长度越短，不同沉陷长度下管道最大位移和预警位移越小。

3)管道发生悬空时，内压越大其管道临界悬空长度越短，在设计内压下管道最大悬空长度约为280 m。