基于合并短线段的直线检测方法

冯 凯，王 琦，于水源

（1.中国传媒大学计算机与网络空间安全学院；2.智能融媒体教育部重点实验室，北京 100024）

0 引言

直线检测一直是计算机视觉领域的研究热点之一。在图像中，直线段属于底层的图像特征，基于直线段的长度、方向和端点检测都能提取出重要而基本的图像信息。在许多计算机视觉任务中都能看到直线检测的影子，如道路检测［1］、消失点检测［2-3］、即时定位与地图构建［4-5］及三维重建［6］等。曲线在人们的日常生活中也随处可见，通过曲线检测能够获取图像中物体的轮廓信息，因此曲线检测与直线检测一样具有较高的研究价值。

目前直线检测已取得了许多研究成果，主要包括边缘连接法和梯度法。霍夫变换算法属于边缘连接法，以其优良的检测能力得到了广泛应用［7］。近年来也有针对霍夫变换的改进算法，包括霍夫一维变换［8］、随机霍夫变换［9］、概率霍夫变换法［10-11］和网格霍夫变换［12］等。但是霍夫变换依然存在针对复杂图像检测性能不佳、容易误检和漏检直线等问题。CannyLines 方法［13］也是边缘连接法中的经典方法，其能够根据图像自适应调整参数，且易于检测低梯度区域，却过滤了一些真实的短线段。梯度法的主流算法包括以下几种：LSD 方法［14］能够有效区别相邻线段，但容易产生过分割的情况；Linelet 方法［15］易于检测细小的纹理信息，但存在运行速度慢、易出现孤立的短线段等缺点。

在曲线段检测方面，目前工业界最常用的还是霍夫变换算法，霍夫变换可根据给定的解析式检测特定曲线（如圆或椭圆），而之后提出的广义霍夫变换［16］可以不需要解析式检测任意给定的曲线。

目前很大一部分线段检测方法都依赖于边缘检测，包括霍夫变换法、EDLines 方法和CannyLines 方法等。Canny算子是目前边缘检测的主流算法之一，其基本思想是找到像素灰度值变化明显的地方作为边缘点。孤立的边缘点可聚集成直线段，再采用某种拟合方法检测直线段即可提取出直线。由此可见，在基于边缘的直线检测方法中，边缘检测算法的优劣将直接影响直线检测效果。

综上，直线检测领域还没有一种通用的高性能方法，只能根据不同情况选择不同方法。优秀的直线检测方法应尽可能避免直线断裂，有较高精度且满足速度要求［17］。为此，本文提出一种基于合并短线段的直线检测方法。实验结果表明，该方法在检测精度和速度方面均表现较好，且该方法既能够检测边缘图中的直线段，也能够检测曲线段。

1 直线检测算法

通常来说，在一张图片中找到所有线段需要较大的计算量，尤其在图片分辨率很高的情况下更是如此。如果将图片切割成多个小矩形框，每个小矩形框中的线段不难检测，再将各矩形框中的短线段合并成直线。当短线段的长度足够短时，即可用来近似曲线段，这种采用逐次近似思想拟合曲线的方式通常被称为“直线简化”。对于直线段检测，该方法最后会输出直线段的两个端点坐标；对于曲线段检测，该方法会输出曲线段上的多个点坐标。

本文方法基本步骤如下：①将图像边缘图切分成若干区域；②通过若干个匹配矩阵检测短线段；③将所有短线段合并成直线或曲线；④探测并补全断裂的线段。

1.1 将图像边缘图切分成若干区域

为了提高算法运行效率与检测精度，对于偏向水平的线段和偏向竖直的线段分开进行检测处理。

（1）针对偏向水平的线段，将边缘图（见图1（a））从左到右切分成若干区域（见图1（b）），也即从左到右设置若干个检测框进行检测。每个检测框的宽度可设置不同数值，该宽度越小，检测到的线段越精细，也能够显示更多细节，图1 中的宽度为8 个像素。

（2）针对偏向竖直的线段，在边缘图中从上到下设置若干个检测框（见图1（c））。

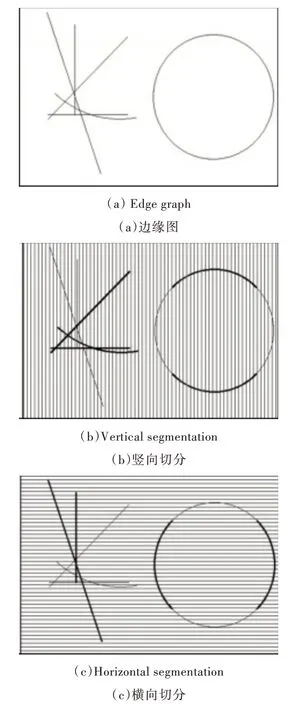
Fig.1 Image segmentation图1 切分图像

这种针对水平和竖直两个方向分别进行处理的思想在Sobel 算子［18］中也能够看到。Sobel 算子包含两组矩阵模板，分别用来检测水平方向和竖直方向的边缘。

1.2 通过若干匹配矩阵检测短线段

通过若干矩阵检测短线段可分为以下几个步骤：

（1）针对寻找检测框中的短线段，本文以其中一个检测框（见图2（a））为例进行说明。首先记录原图中直线与检测框边界的交点，左右两个交点确定一条直线，图2（a）检测框的左边界检测到4 个交点，右边界检测到4 个交点，即可确定16 条短线段（见图2（b））。

（2）如果左右两点纵坐标的差大于检测框宽度，则是一条倾向于竖直的直线，剔除该短线段。在这一步能够排除大部分短线段，上一步的16 条短线段经过这一步只剩下5 条可能的短线段（见图2（c）），减少了很多后续计算量。

（3）目前需要判断上一步的5 条短线段在原始图像中是否存在。具体方法如下：预先构造一个字典Map，字典中包含15 个短线段匹配矩阵，即图3 中的15 幅短线段匹配二值图。已知倾向水平短线段的左右端点坐标，即可在原图像中框选需要检测的短线段区域，得到矩阵M1（图2 中框选部分）。将短线段左右端点的纵坐标之差作为键，从字典Map中取得一个短线段匹配矩阵M2（图3 中框选部分）。将矩阵M1与矩阵M2点乘，得到结果矩阵M3。计算矩阵M3的各元素和Sum。如果Sum大于一个阈值，则可认为假设的短线段在原图中存在。剔除Sum小于该阈值的短线段后得到3 条短线段（见图2（d）），即该检测框检测到了3 条水平短线段。

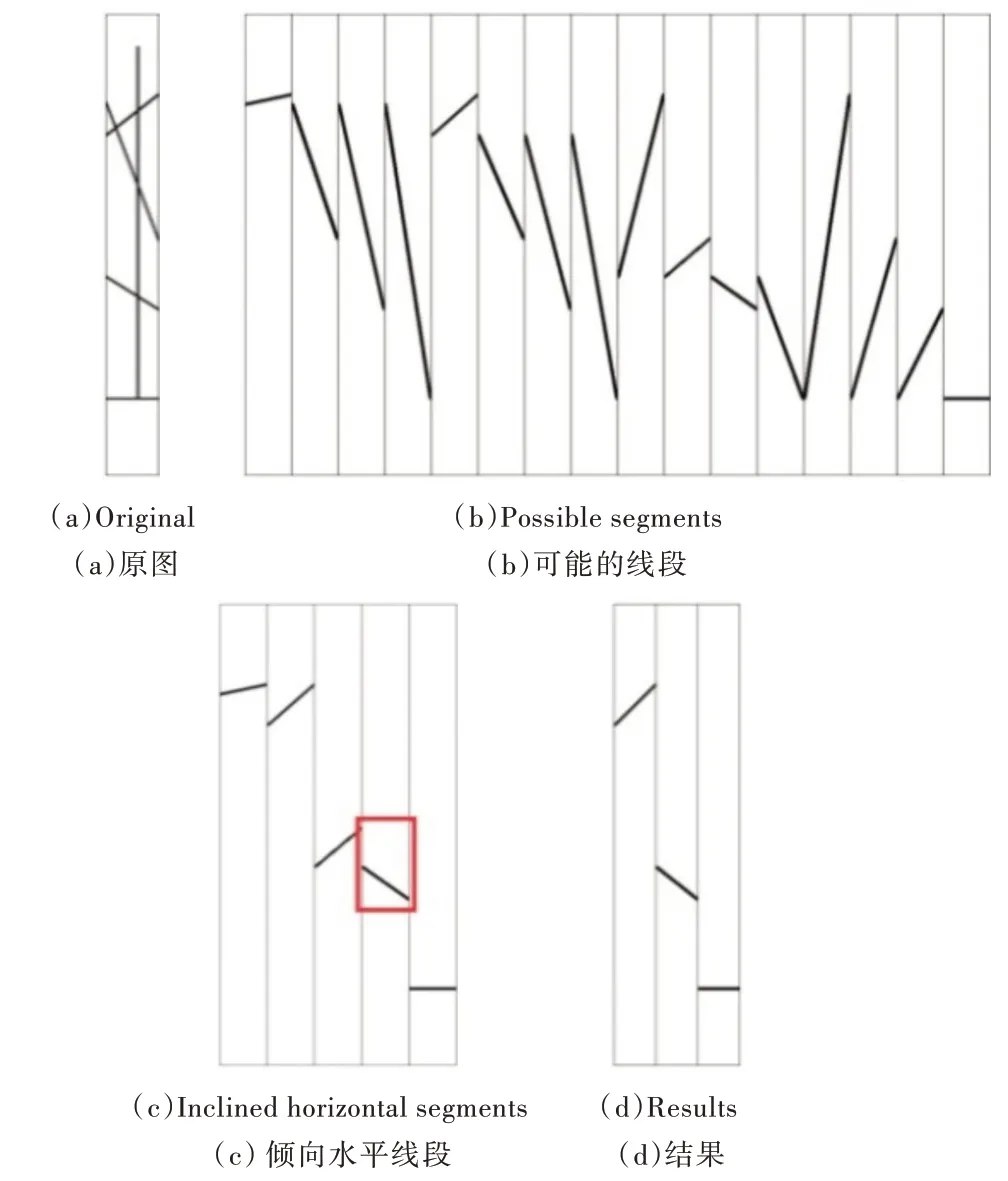
Fig.2 Short line detection图2 探测短线段

Fig.3 Binary graph matching short line segments图3 匹配短线段二值图

1.3 合并检测框中的短线段得到直线

之前检测到的短线段是零散的，每一条直线的各个短线段分散在不同检测框中，需要将其合并起来得到一条直线。例如图4（b）中的直线由4 条短线段组成，它们分别被4 个检测框探测到，即图4（a），下面是合并思路：从左向右遍历未标记的短线段，以当前短线段L1第二个交点的纵坐标为索引值，在下一个检测框的短线段集合中寻找下一条短线段L2。当短线段L1与短线段L2的角度差小于1 时，两条短线段可合并为一条直线。当两条短线段角度差大于1且小于30 时，两条短线段可合并为一条曲线。

1.4 探测并补全断裂的线段

由于本方法将偏向水平和偏向竖直的线段分开进行检测，在进行曲线检测时，那些倾角在45°和135°附近的线段会断裂，例如图1（b）、（c）中的圆被划分为4 段曲线。因此，需要在线段端点附近寻找断裂的线段，具体思想如下：图5（a）中的L0为原曲线，图5（b）为短线段合并后的线段，其中L1与L2之间是断裂的，R5为L1所在方格，R2为L2所在方格，需要在R5的八邻域方格内寻找与L1相连的线段L2，判断图5（c）中的虚线是否为断裂线段的方法为1.2 节中步骤（3）中的方法。图5（d）表示通过逐次近似的方法拟合图5（a）中曲线后的效果。

Fig.4 Merging short segments图4 合并短线段

Fig.5 Line segment for detecting fracture图5 断裂线段探测

2 实验

2.1 实验设计

考虑到本文算法既能检测边缘图中的直线，又能检测曲线，针对这两种情况应设计不同实验进行分析。

为了验证本算法检测边缘图中直线的效果，本文采用案例检验和客观评测系统两种评测方法进行测试。首先选取两幅图像进行案例检验，分别是Lenna 图和五角大楼。为了验证该算法检测边缘图中直线的效果，本文还将其与霍夫变换算法和LSD 算法进行比较。

案例检验属于定性分析，对于复杂图像，很难仅通过视觉感知对检测结果进行比较［19］，而客观评测系统将使用York 城市数据库［20］评测本文算法，属于定量评测方法。York 城市数据库是一个包含102 张原始图像的数据库，而且每张图像都人工标注了图像中直线段的相关信息（包括直线段端点坐标）。之后Cho 等［15］花费大量时间对该数据库进行了详细的标注工作，能够较为客观地评价直线检测算法效果。评价一条直线是否被正确检测的标准如下：对于人工标注的直线段加粗一个像素进行处理（加粗一个像素表示可容忍的检测误差为一个像素），然后判断检测的直线段是否在该该加粗的直线段内，判断方法为1.2 节步骤（3）中的方法。由此可得到正确检测的直线，继而计算出误检和漏检的直线段。

对于曲线检测，本文采用案例检验方法进行评测，选取两幅图像处理领域的经典标准图片进行检验，分别为水果和帆船。

2.2 实验分析

2.2.1 直线检测（使用案例检验测试）

图6 为Lenna 图与五角大楼图（彩图扫OSID 码可见），为了更清晰地观察到结果，在原图中截取了一部分作为局部放大图，分别在图中的第2 列和第4 列。其中图6（a）为原图，图6（b）为预处理后的边缘图，图6（c）为采用本文算法检测的结果，图6（d）为采用霍夫变换算法检测的结果，图6（e）为采用LSD 算法检测的结果。表1、表2 为不同结果的对比。

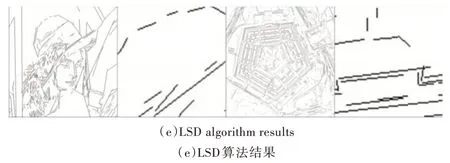
Fig.6 Effect Comparison of different methods图6 不同方法效果对比

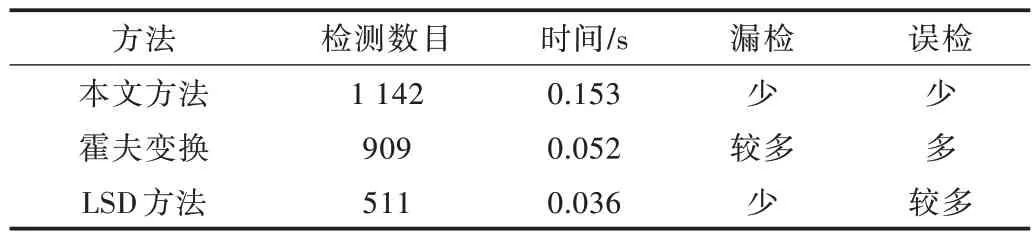
Table 1 Comparison of different results of detecting the lines in the left figure of Fig.6（a）表1 图6（a）左图中的直线检测结果对比

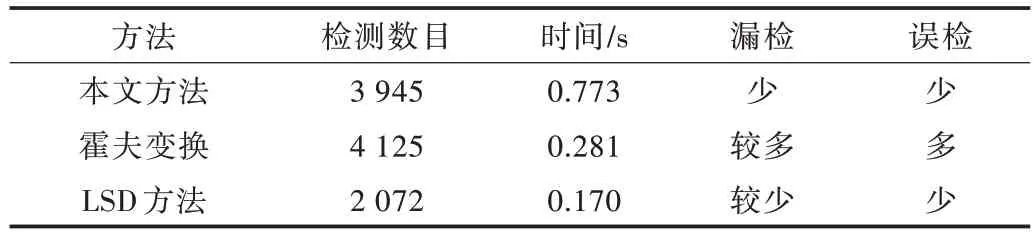
Table 2 Comparison of different results of detecting the straight line in the right figure of figure 6（a）表2 图6（a）右图中的直线检测结果对比

比较本文方法与其他方法的检测结果，从图6 中可观察到，霍夫变换在图像边缘密集（比如纹理）情况下的直线检测效果并不好，常常是错误而杂乱的，具体表现在Lenna的头发和眼睛上。霍夫变换还存在很多漏检的直线，比如Lenna 的帽子边缘没有被检测到，从图6 中五角大楼的局部放大图也可看出霍夫变换算法误检了许多短线段。LSD 算法的检测效果不太稳定，在Lenna 图中，可明显看到在帽顶处漏检了一些直线段，由此造成图像主体边缘的不连续，同时对于五角大楼局部放大图中的停车场也漏检了许多短线段。由表1、表2 可知，相比霍夫变换算法和LSD 算法，本文方法误检和漏检的情况较少。

2.2.2 直线检测（使用客观评测系统测试）

图7（a）为York 城市数据库中的一张原图像，图7（b）为边缘图像，图7（c）为人工标注的直线段图像。从图7（d）中可以看到，霍夫变换方法得到的直线段在图像中某些区域堆积在了一起，尤其是短线段。从图7（e）中可以看到，LSD 方法存在明显的误检直线，例如图上方1/6 处有一条斜线被误检成了水平线。图7（f）为本文方法检测结果，相比霍夫变换方法，本文方法不会在线段密集部分误检率较高，也不会像LSD 方法那样出现明显错误。

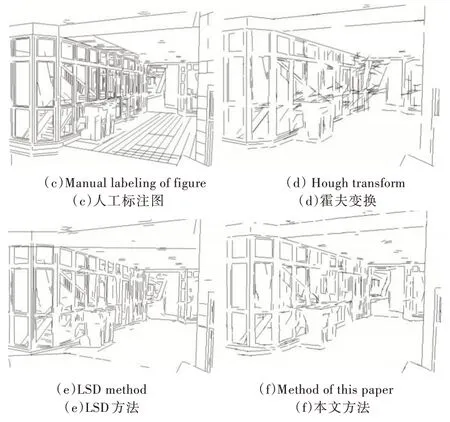
Fig.7 Detection effects of different methods图7 不同方法检测效果

在Youk 城市数据库中，平均每张图片有680 条标注线段，102 张图片的直线段总长度约为3 475 980 个像素。令TP为真阳性（正确检测直线长度和），FP为假阳性（误检直线长度和），FN为假阴性（漏检直线长度和），本文将根据以下4 个指标对不同方法进行评估：

（1）精度。即正确检测直线占检测到所有直线的比率，计算方法如下：

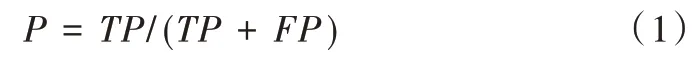
（2）召回率。即正确检测直线占人工标注直线的比率，计算方法如下：

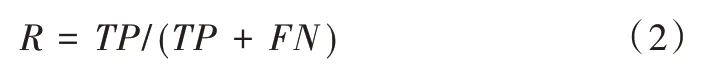
（3）IoU。即正确检测直线与人工标注直线的交集比上它们的并集，计算方法如下：

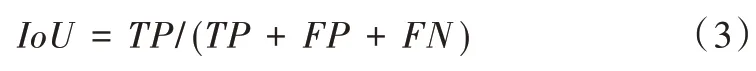
（4）F值。即精度和召回率的调和平均数，本文设F 值中的β 值为1，计算方法如下：

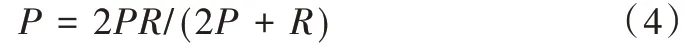
根据表3 能从整体角度分析不同方法的检测效果，可以看出本文方法的检测精度高于霍夫变换方法和LSD 方法，而召回率、IoU和F值更是远高于其他两种方法，说明本文方法的检测效果优于传统主流方法。

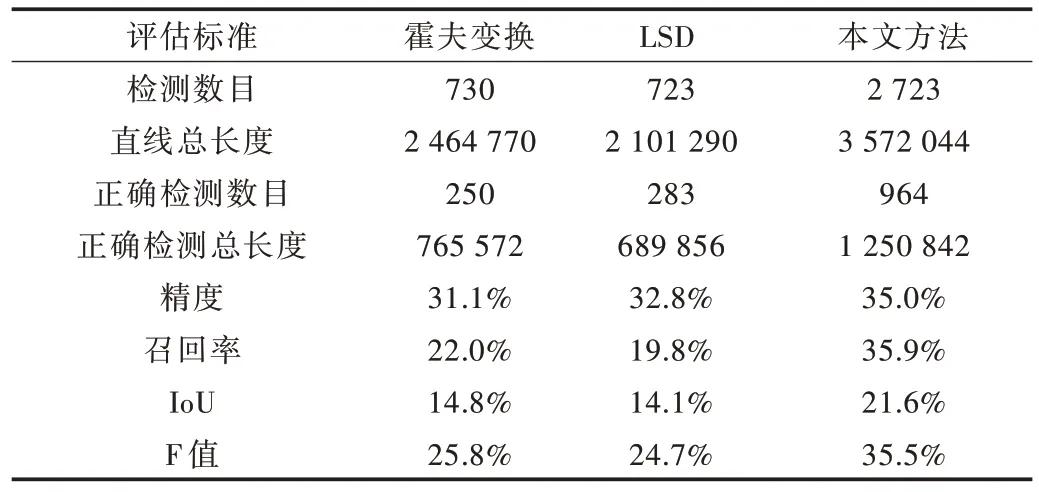
Table 3 Evaluation results of line segment detected by different methods表3 不同方法检测直线段评估结果

2.2.3 曲线检测

图8 为水果和帆船（彩图扫OSID 码可见），其中第2 列与第4 列为局部放大图。图8（a）为原图，图8（b）为边缘图，图8（c）为采用本文算法检测的结果。

从图8、表4 中可以看出，本文方法检测曲线的效果也较好，采用本文方法可以检测任意形状的曲线，而传统方法需要通过曲线解析式检测曲线，本文方法突破了这一局限。

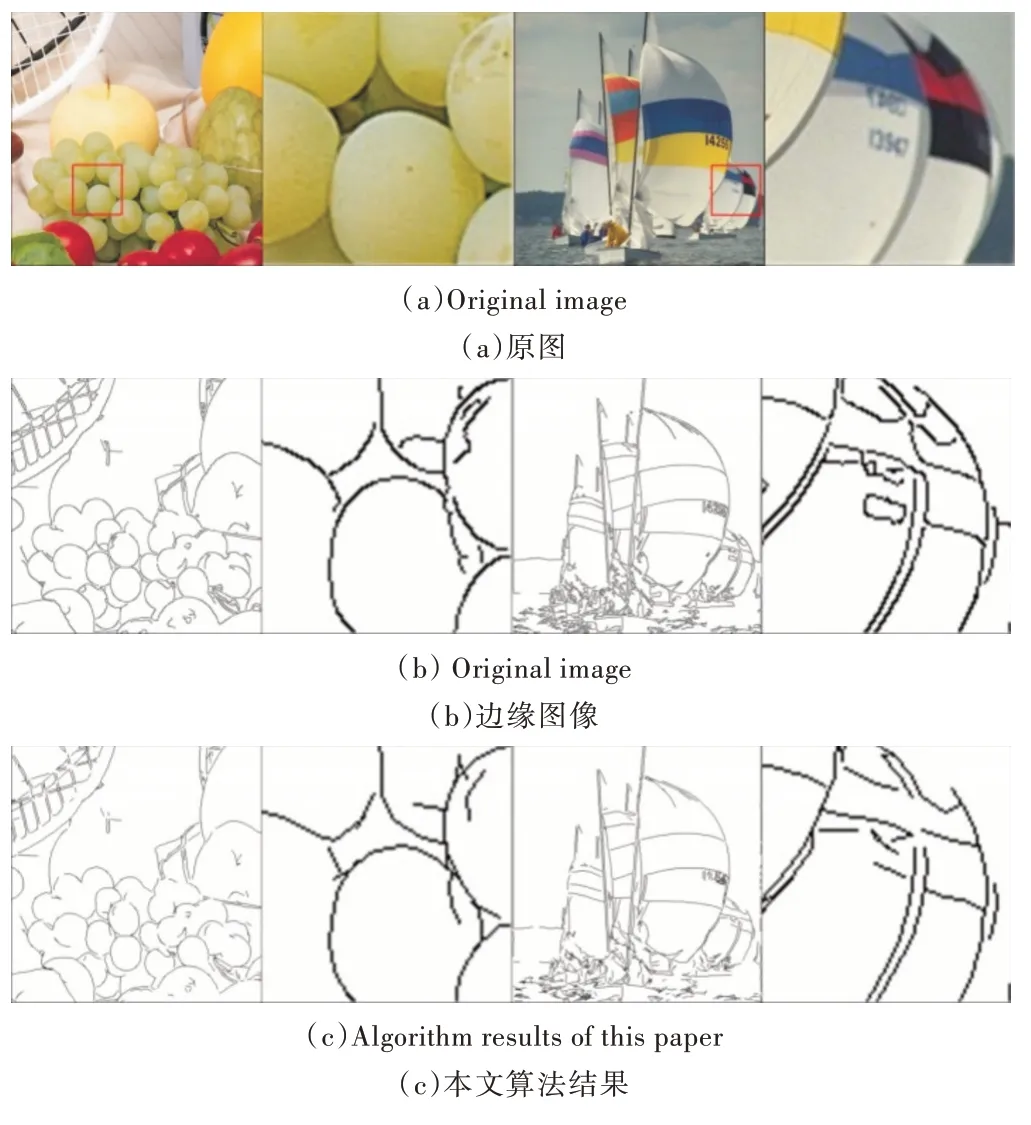
Fig.8 Curve detection effect of this method图8 本文方法检测曲线效果

Table 4 Comparison of different curve results表4 曲线检测结果对比

3 结语

本文提出一种新的直线检测方法，该方法采用分段检测思想。将本文方法与其他直线检测算法进行对比，并在包含York 城市数据库的客观评测系统中进行测试，结果表明，直线漏检和误检的情况都较少，在边缘较复杂的图片检测中依然表现稳定，鲁棒性较好。经过案例检验测试，发现该算法在曲线检测上也有良好效果。另外，本文检测的曲线属于一般性曲线，在现有基础上，可考虑改进检测曲线的方式，如在算法中引入特殊曲线（圆和椭圆等）的曲线解析式，进而使得该算法更加贴近实际应用。