改进Apriori 算法在学生能力影响因子分析中的应用

刘 磊，康瑞华

（湖北工业大学计算机学院，湖北武汉 430072）

0 引言

随着信息技术的发展与智能时代的到来，社会教育系统的变革逐渐频繁，学生综合素质能力培养显得尤为重要。本文通过对2 000 多名来自不同地域、不同学校与不同专业的大一、大二学生的问卷调查，应用Apriori 算法分析其学习生涯中曾进行的能力培养对当前大学时期综合素质的影响，从而给予当前学生成长过程中多元化教育选择以方向性指导［1］。

1 相关研究

大数据是继云计算、物联网之后，计算机行业又一次颠覆性的技术革命。大数据挖掘与应用可创造出很高的经济价值，将是未来计算机领域最大的市场机遇之一［2］。大数据的应用在生活中也屡见不鲜，例如大数据在电视台数据处理中的应用［3］、大数据在金融投资中的应用［4］、关联分析在教育领域的应用等［5-17］。

在大数据应用过程中，其常常引发人们对算法本身的思考。我国近年来在大数据分析领域的研究进展很快，在研究起始阶段，刘君强等［18］收集整理近年来关于关联规则的详细研究，针对大数据分析领域的新进展进行综述与分析，并根据基础大数据分析算法Apriori 的特点，提出Apriori 算法优化的初步方向与思想。之后，王伟勤等［19］提出改进Apriori 算法的具体内容，即采用基于数组，且避免Apriori 的匹配模式，通过只扫描一次，同时减少算法内存占用空间的方式提高算法效率，并对该方法进行验证，但其仍存在两个关键问题：扫描次数与剪枝效率。本文在此基础上对扫描方式和数据结构存储两个关键问题进行优化与改进，通过分析学生能力影响因子，探究Apriori 算法的改进思路与方法。

2 Apriori 算法

Apriori 算法常用的频繁项集评估标准有3 个：支持度、置信度和提升度。其中，支持度是关联数据在数据集中出现的概率，支持度高的数据不一定构成频繁项集，但是构成频繁项集的数据支持度肯定不低。置信度则体现一个数据出现后，另一个数据出现的概率，即数据的条件概率。如大学生幼年培训奥数对应钢琴的置信度为60%，支持度为5%，说明总共有5%的学生在幼年培训了奥数和钢琴，培训了奥数的学生中有60%的人培训了钢琴。提升度则表示两个数据之间的管理关系，也即在培训奥数的情况下同时培训钢琴的概率与培训钢琴总体发生概率之比。若提升度大于1，则钢琴⇐奥数是有效的强关联规则；若提升度小于等于1，则钢琴⇐奥数是无效的强关联规则［8，14-16］。

Apriori 算法采用逐层搜素策略，同时依据其性质压缩搜索空间。其基本思想在于，首先扫描一次事务数据集，找出频繁一项集集合L1，然后基于L1产生所有可能的频繁二项集即候选集C2，筛选出候选项集C2中所有满足最小置信度的项集，组成频繁项集L2。用上述步骤重复处理新得到的频繁项集Lx，直至再也找不出频繁项集时退出［17-19］。

在Apriori 算法中，候选项集的生成可分成连接和剪枝两部分。为提高剪枝效率，运用了以下两个重要定律：

定律1 如果k维数据项Xk是频繁项集，则其k-1 维子集都是频繁项集。

定律2 如果k-1 维数据项Xk-1不是频繁项集，则其k维超集都不是频繁项集。

2.1 Apriori 算法改进思想

Apriori 算法得到了广泛运用，主要由于其算法结构简单易懂、便于理解，没有复杂的公式推导［2］。通过运用两个重要定律，使得算法候选集的规模大幅减小，相应算法运算速度大幅提高，但其仍存在两个影响内存及效率的问题：①事务数据库扫描次数过多。每次寻找频繁项集都需要扫描一次事务数据库，最终寻找到长度为k的频繁项集共需扫描k次，所以当数据库或k很大时，算法耗时将呈几何式增长；②在执行候选集的剪枝操作时，对数据库的扫描次数过多。而且当候选集与自身连接时也要对数据库进行多次扫描，导致算法在广度优先方面的适应性很差［10-13］。

本文将从两方面对现有Apriori 算法进行改进：

（1）针对事务数据库扫描次数过多的问题，本文主要借鉴了文献［4］的思想，采用与传统Apriori 算法不同的数据结构，将水平的事务数据库（见表1）转变为垂直的数据结构（见表2）。

Table 1 Transaction database表1 事务数据库

Table 2 Project database表2 项目数据库

通过这种转换将事务数据库垂直化，只需扫描一次数据库即可完成数据分析，并且更容易得到支持k维数据项的事务数。

（2）针对冗余数据项过多、剪枝次数过多以及连接产生数据项空间较大的问题，本文利用算法的两个定律推断出第3 个定律：

定律3 对于k维数据项x={i1,i2,i3…,ik}，如果存在一个元素j⊆x，使表示在k-1维频繁项集中包含j的数量)，则x不是频繁项集。

证明：若x是k维频繁项集，则由定律1 可得，其共有=k个k-1 维子集为频繁项集，其中包含j的共有=k-1 个。由于上述子集均为频繁项集，故得到≥k-1，与假设矛盾，所以x不是k维频繁项集。

从这一定律可以得出：如果在Lk-1中有一元素j，且有＜k-1，则所有包含元素j的k-1 维频繁项集不参与连接。

2.2 改进后的Apriori 算法描述

相关定义如下：

3 数据分析

本文通过分析当前中小学教育政策、大学生培养计划、企业需求以及大学新生心理，设计了关于大学生能力培养方式与当前时期适应力、自信心的调查问卷，并通过问卷星发放到包括985、211、普通高校在内的10 所高校，回收问卷共计2 812 份。之后使用Apriori 算法进行数据分析，Apriori 算法是一种挖掘布尔关联规则频繁项集（Bourg association rules frequent itemsets）的经典算法，用来寻找数据值中频繁出现的数据集合。本文通过寻找当前大学生曾经参与过的多元化培训对其综合素质与自信心影响最大的特征数据结果集，根据该结果集为当前教育过程中的多元化能力个性培训提供指导性方案。

根据大学生当前的综合素质情况对2 812 份调查问卷进行分类，并设计特征因子与权值，运用本文改进的Apriori算法进行分析。

3.1 垂直数据库建立

将收集的数据按照表2 的数据结构录入项目数据库，调查结果中的每一项包含多个选项，如果每个选项都由一个数据进行记录，则需要庞大的数据空间进行记录（若有4个选项则需4 位，但采用下述方法只需2 位）。在实际数据分析过程中，为每个选项进行编码，如针对“结业成果是否有用”这一项，可进行如下二进制编码：00：有很大作用；01：有作用但不大；10：基本没什么作用。该方法相比位存储有效减少了数据存储空间。为更直观地理解算法过程，下述分析示例不按以上方法进行编码处理，而是直接用数据名称表示，如表3 所示。

Table 3 Diversity capability database表3 多元化能力数据库

3.2 改进Apriori 算法数据分析

设置最小支持度0.3 后，由扫描数据库得到频繁一项集，如表4 所示。

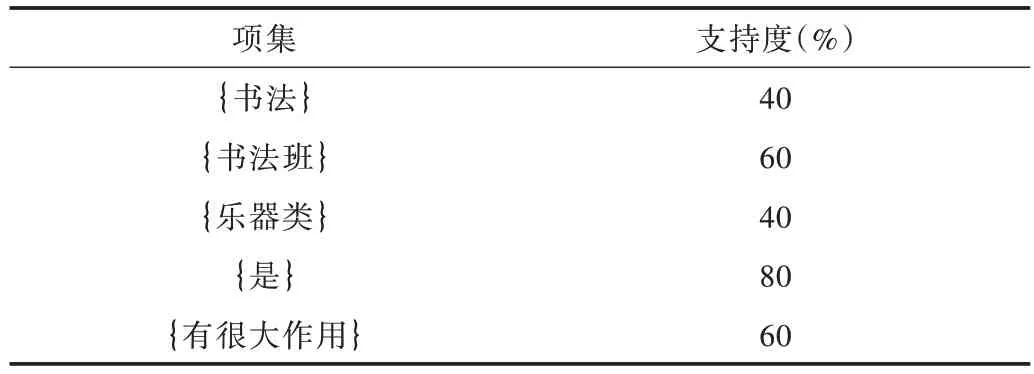
Table 4 Frequent itemsets L1表4 频繁一项集L1

由于当L1不存在需要剪枝的元素即可进行连接，通过连接筛选得到L2，如表5 所示。

此时进行剪枝，其元素列表为｛书法，书法班，乐器类，是，有很大作用｝，所有元素均符合约束，所以无剪枝项，连接并筛选得到L3，如表6 所示。

Table 5 Frequent binomial sets L2表5 频繁二项集L2

Table 6 Frequent trinomial sets L3表6 频繁三项集L3

再次进行剪枝操作，由于｛书法｝的数量少于3 即可进行剪枝，此时元素列表为｛书法班，乐器类，是，有很大作用｝，连接筛选得到L4：｛书法班，乐器类，是，有很大作用｝。

通过改进Apriori 算法，并设置min_sup为0.40，对收集到的数据进行关联规则分析得出以下频繁项集，如表7 所示。

Table 7 All frequent itemsets表7 所有频繁项集

由表7 可知，｛主动参加，成果有很大作用｝与｛乐器类，主动参加｝属于频繁项集，表示学生主动参加并觉得成果有很大作用的概率相对较大，其具有高置信度，说明学生在主动参加特长班之后，有很大概率认为成果有很大作用。对于第二个频繁项集，亦可用相同思想进行分析。

4 实验结果

根据本文的改进Apriori 算法思想，将上述数据整理分析过程与传统的Apriori 算法分析过程从数据量与运行时间两方面进行对比。具体说明如下：

（1）测试环境：本次测试采用Python 语言编程，操作系统为Windows 10，处理器为Intel 酷睿i7-6500 双核处理器，内存大小为8GB。

（2）测试结果：通过对2 800 多份问卷进行分析，提取特征数据，并针对不同数据量进行测试与对比，得到结果如图1 所示。

通过图1 可以看出，本文提出的改进Apriori 算法相比传统Apriori 算法可以有效缩短运行时间，加快数据处理速度。而且随着数据量的增加，算法效果有一定程度提升。

Fig.1 Comparison of running time of each data volume test图1 各数据量测试运行时间对比

5 结语

本文提出的改进Apriori 算法主要思想来自于两个方面：①改变数据库结构为项目数据库结构，传统的事务数据库结构会造成多次扫描数据库，带来很大的时空开销［time and memory-consuming］，而采用项目数据库结构只需扫描一次即可完成整个算法的运行；②根据算法特性设计剪枝操作，相比传统算法的剪枝操作，在一定程度上能够提升算法性能。改进Apriori 算法在不同数据量情况下对传统算法的提升效果不同，当数据量为8 000 时，改进Apriori 算法的运行时间相比传统算法缩短了7.15%，算法效果得到了相当大程度的提升。但不足之处在于当数据量很大时，依旧需要大量时空开销，其开销主要存在于剪枝操作中。若能找到更好的剪枝操作方法，则能对算法作进一步改进。