基于Mean Shift 的公交下车站点判定方法

温晓丽，何子登，余红玲，邹大毕

（广州羊城通有限公司，广东广州 510080）

0 引言

近年来，随着广州市城镇化发展进程加快，城市公交线网面临越来越大的压力，研究如何提升交通运行效率、优化公交线网布局、升级交通出行服务等成为业界关注的焦点。目前，广州市公交车普遍安装了进出站监测系统与车载GPS 导航定位设备，按时序记录公交车进出站信息及GPS 行车轨迹数据。所有连续运行的公交车辆和众多的乘客刷卡交易形成了城市公共交通运行及乘客出行大数据，但公交收费多采用“一票制”，只有上车刷卡数据，没有下车刷卡数据。为进一步研究乘客出行时间、空间及公交系统客流量特征，首先需要确定乘客公交下车站点及下车时间，以公交IC 卡为主的数据分析方法仍是当前公交客流OD 研究的主流做法。国外学者的研究大多基于出行链思想，利用AFC、车辆自动定位系统、地铁公交联合数据等，分析推导公交客流与出行时间变化特征等，并验证城市交通出行过程的连续性［1-8］。国内学者研究主要集中于IC 卡下车站点的推导，如胡郁葱等［9］通过IC 卡数据挖掘技术获取公交OD 矩阵；陈峥嵘［10］将智能公交数据处理方法应用于公交客流OD 研究；胡继华等［11］提出结合出行链的IC 卡公交客流研究方法。

本文以广州市一卡通交易数据为实例进行分析研究，根据出行链思想，对乘客的连续交易行为进行分析。以卡交易数据、公交进出站数据和线路站点数据为基础，针对完整的公交出行链，提出一种可判定公交下车站点的最近邻算法；针对出行链不完整的情况，根据乘客长期出行的时空规律性，通过分析用户中长期历史交易情况，提出采用Mean Shift 算法计算乘客的居住地（O）和工作地（D），再利用OD 预测不完整出行链里交易记录的下车站点［12-14］。通过这两种方法，可补充85% 的公交交易数据，并抽取部分用户的下车站点数据进行验证。结果表明，该方法准确率较高，因此具有一定的研究价值。

1 数据简介

本文数据来源于广州羊城通卡在公交、地铁场景下的交易数据，公交公司提供的每天进出站数据以及线路站点数据。在“一票制”收费模式下，公交交易数据中包含逻辑卡号、车辆车牌号、班次、线路编码、上车站点编码、上车站点及其经纬度、上车时间等信息，但不包含下车站点和下车时间信息。地铁交易数据中包含逻辑卡号、地铁进出站站点、进出站时间以及进出站站点经纬度等信息。

公交车的进出站监测系统记录了所在公交车辆的进出站数据，公交交易数据与公交进出站数据之间存在着对应关系。每辆车都有一个智能调度编号，根据该编号对进出站数据预先划分好班次，如表1 所示。

Table 1 Bus frequency information表1 公交车辆班次信息

Table 2 Bus line stop information表2 公交线路站点信息

在下车站点判定过程中，本文提出采用地铁数据和公交数据联合分析的方法，采用基于出行链的乘客下车站点概率模型进行下车站点判定。

2 最近邻推算下车站点算法

基于广州市公交交易和地铁交易的融合数据，按照每个用户刷卡进站或上车时间对所有交易排序，分析每天有N（N＞1）次乘车记录的乘客出行特点。本文将广州市常驻人口每天的出行划分为居住地和工作地，居住地和工作地范围内聚集公交站点或地铁站点。大多数上班族用户每天上午从居住地选取一个站点出发，下午从工作地选取一个站点乘车回家。假定这些乘客的出行链是闭合的，则用户出行方式可归纳为以下两类情况，如图1 所示。

第一类为对称出行，这类乘客的出行路径可归纳为H-＞W-＞W-＞H，中间没有换乘或仅有一两次换乘，这类乘客最典型的代表就是通勤族或学生；第二类为非对称出行，这些乘客的出行路径归纳为H-＞T1-＞T2-＞T3-＞H（Ti指临时地），中间可能经过一次或N 次临时换乘站点，其出行不具有时空规律性。

假设乘客在一次乘车记录中，上车站点为Si，Si∈LA，所属线路是LA｛S1，S2，S3，…｝，则此次下车站点Sj满足如下条件：Sj∈Li，j＞i。

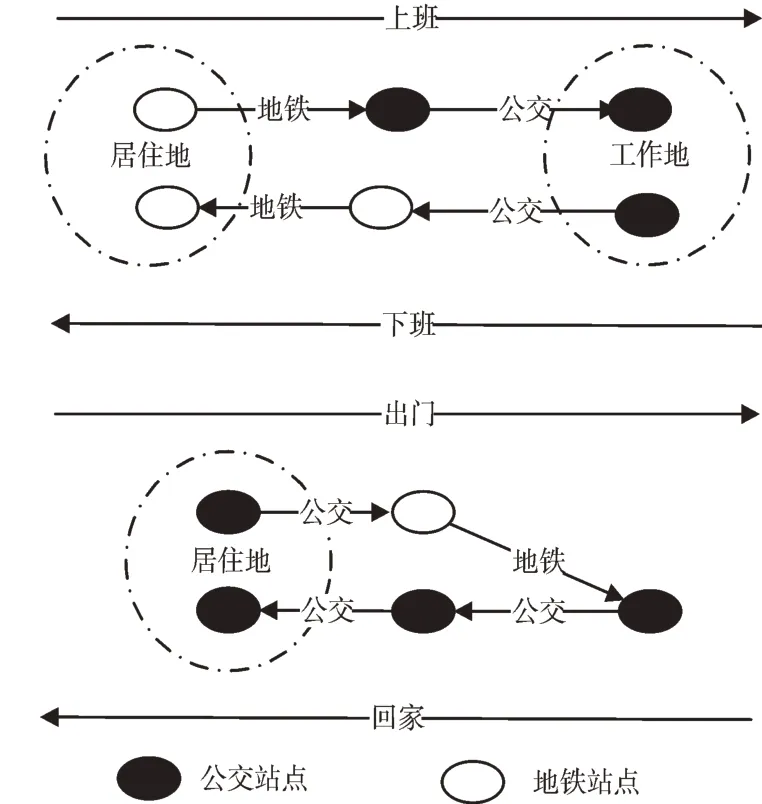
Fig.1 User travel mode图1 用户出行方式

最近邻下车站点判定可描述为：

（1）按天输入某个用户按进站时间排序的交易信息列表：lno：｛on_station_time1，on_station_time2…，on_station_timei，… on_station_timelast｝。

（2）如果只有一条记录，先不作处理。如果有多于两条记录，按顺序读取第i 条和i+1 条，如果i 是最后一条记录，则读取第i 条和0 条。从0 开始遍历信息列表，分别读取相邻两次刷卡站点为Si和S（i+1）%last。相邻两次交易的下车站点判定如图2 所示。

受道教风水学说的影响，古代朝鲜创作了众多堪舆主题的小说，在这些小说中，堪舆成为小说叙事的主线，贯穿故事始终。 如《定名穴牛卧林间》中，讲述了湖西士人为得名穴，诚意侍奉地师朴尚义，无奈朴尚义恃术骄纵，千般推辞，湖西士人一怒之下剥掉朴的衣服，将其紧缚于松树上。 恰巧遇到尹氏搭救，朴尚义才幸免于死。 朴感念尹氏的再生之恩，遂帮助尹氏相地，但终未告知吉穴所在。 后来尹氏遍请地师占正穴，仍然求之不得。 一日，竟在牛卧之地得到正穴。 移葬亲山后，家族逐渐显赫起来。

Fig.2 Off site determination of two adjacent transactions图2 相邻两次交易的下车站点判定

（3）判断遍历到的相邻两条记录是否属于B-＞B，B-＞R这类换乘方式，如果属于这两种情况，计算Si站点所在线路下游站点LA｛Sj｝，j＞i。计算下游每个站点Sj与S（i+1）%last的欧式距离D（Sj，S（i+1）%last），如果D（Sk，Sj）＜d（d为指定的一个距离阈值），则放入备选集合R｛S1，S2，S3…｝。如果相邻两条交易记录为R-＞R，R-＞B，则不作处理。

（4）计算结果集的所有D（Sj，S（i+1）%last）距离，选取其中的最小距离min（D（Sj，S（i+1）%last））站点作为第i 条公交交易记录的下车站点。如果R 为空，说明下游每个站点Sj与S（i+1）%last的距离都不小于d，认为出行链断裂，先不作处理。对于第i（1＜i＜last）条公交交易记录，属于中途断裂的，无法确定其下车站点。在R 集中，如果最小站点距离为0，则属于同站换乘。

3 Mean Shift 算法

3.1 Mean Shift 算法计算OD

每个乘客的居住地或工作地附近会有很多不同的公交站点或地铁站点，乘客会选择不同的站点乘车上下班。分析乘客的长期交易记录，采用求密集点中心的方法得出居住地或工作地的中心点。每一个密集点中心有一个点x，周围有很多个点xi，采用Mean Shift 算法计算点x 移动到每个点xi所需的偏移量之和，求平均数后得到包含大小和方向的平均偏移量（该偏移量方向是周围点分布密集的方向）［14-17］。然后，点x 往平均偏移量方向移动，再以此为新起点不断迭代，直到满足一定条件后结束。

给定d 维空间Rd的n 个样本点，i=1，…，n，在空间中任选一点x，则Mean Shift 向量基本形式定义为：

Sk是一个半径为h 的圆形区域，满足以下关系的y 点集合：

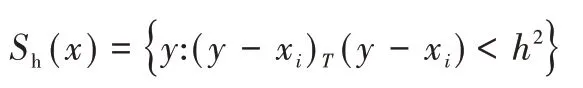
k 表示在n 个样本点xi中，有k 个点落入Sh区域。在二维坐标中任选一个点，然后以该点为圆心、h 为半径作圆。落在该圆内的所有点和圆心都会产生一个向量，向量以圆心为起点，以落在圆内的点为终点，然后将这些向量相加求平均得到Mean Shift 向量。如图3 所示，灰色箭头为Mh（Mean Shift 向量），以Mean Shift 向量终点为圆心，再作一个二维的圆。重复以上步骤，可再得到一个Mean Shift 向量，如此重复，Mean Shift 向量收敛至概率密度最大的地方。

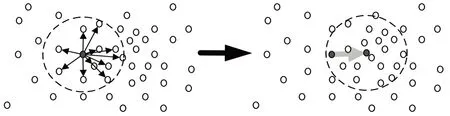
Fig.3 The process of finding the center of dense points图3 求密集点的中心点过程

结合广州市常驻人口在工作地和居住地的实际出行场景，根据乘客通勤出行的时空规律性，分析地面和轨道交通中长期的海量交易数据。假定用户工作日上午最早的一次交易记录或非工作日第一次交易记录的上车站点坐标＜home_lon，home_lat＞属于居住地范围，工作日下午最晚一次交易记录的上车站点坐标＜work_lon，work_lat＞属于工作地范围。

少数情况下可能先以非公交方式中途换乘其它地点，再搭乘公交回居住地。这些非工作地或居住地的坐标较为离散，可采用Mean Shift 算法求密集点的中心点。分析多天的居住地坐标｛＜home_lon1，home_lat1＞，＜home_lon2，home_lat2＞，＜home_lon3，home_lat3＞…｝，得到用户居住地的中心点O，并用类似方法得到用户工作地的中心点D。

3.2 断裂出行链的OD 补充算法

（1）出行链尾部断裂的下车站点算法。lno：｛on_station_time1，on_station_time2…，on_station_timei，…on_station_timelast｝，on_station_timei＜13：00：00。针对实际场景中乘客出行记录都在上午的情形，通过最近邻站点算法进行计算，判断当天最后一次交易记录和首次交易记录的结果集R 是否为空，如果不为空，这些乘客在上午完成一次H-＞T-＞H（T 指临时地）；如果为空，说明乘客出行链断裂，不是回家。对于这些出行链尾部断裂的乘客，假定是前往工作地，如图4 所示。针对当天上午最后一次公交交易记录，计算下游站点与工作地中心点D 的距离D（Sj，D），设定另外一个阈值d2，从小于d2的结果集R 中选取距离最小的站点作为最后一次公交下车站点［18-21］。

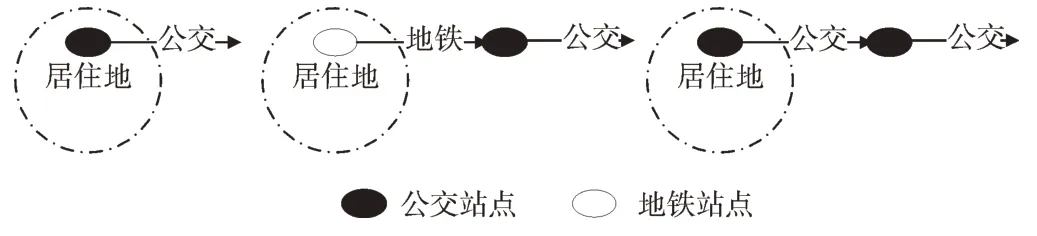
Fig.4 The end of travel chain is broken图4 出行链尾部断裂

（2）出行链头部断裂的下车站点算法。lno：｛on_station_time1，on_station_time2…，on_station_timei，…on_station_timelast｝，on_station_timei＞13：00：00。针对实际场景中乘客出行记录都在下午的情形，假定这些乘客无论是否上班，最终都要回居住地。对于出行链头部断裂的乘客，计算与居住地中心点O 的距离小于d2的结果集R，从R 中选取距离最小的站点作为最后一次公交的下车站点，如图5所示。

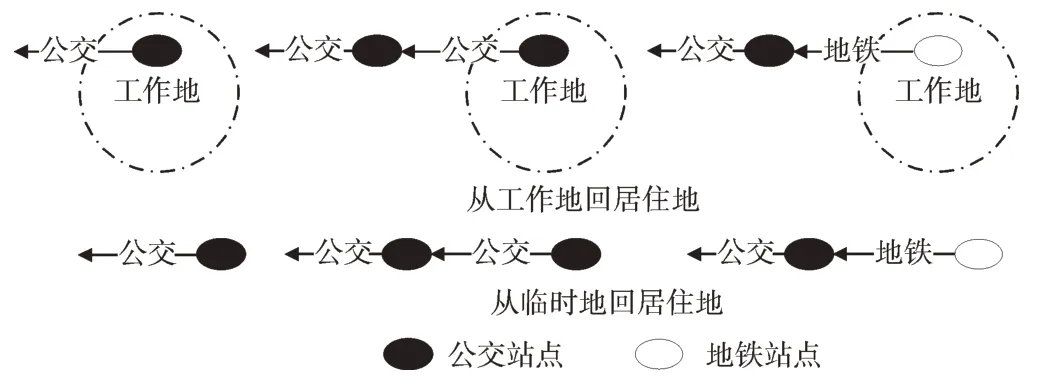
Fig.5 The head of travel chain is broken图5 出行链头部断裂

（3）不可预测的断裂出行链。经过上述两步处理后，对于R 集合为空的情况，这类乘客的出行链被划分为不可预测的断裂出行链。这类乘客中途可能因为其它原因选择非公交的其它出行方式，或者下班后去其它地方，或者上午不去上班，无法作出预测，如图6 所示。

Fig.6 Situations unable to predict the drop-off point图6 无法预测下车站点的情形

3.3 下车时间补充

进出站信息表里记录了每辆公交在每个班次进入每个站点的时间enter_time。通过上述两阶段能确定下车站点名称off_station_name 和下车站点编号off_station_no，根据乘客当天所乘公交车的车牌号、所属班次信息，联合当天进出站信息中对应车辆的车牌号、班次信息，并根据下车站点编号对应的下车站点信息，以enter_time 时间补充作为此交易记录下车站点的下车时间。

4 实验结果与分析

以广州市2019 年12 月12 日的公交和地铁交易数据为例进行研究，剔除站点坐标有误差的交易记录，提取样本总交易记录1 413 202 条。根据站点服务便利水平，设置连乘距离阈值d=1km。第一阶段补充下车站点数据为769 370，占总数据量的55%，如表3 所示。

Table 3 Supplementary drop-off station of the first stage表3 第一阶段补充下车站点

实验进一步采用Mean Shift 算法计算乘客居住地与工作地的中心坐标，分析近2 个月的公交地铁交易数据，得出用户的OD 坐标信息（居住地中心和工作地中心），如表4、表5 所示。

第二阶段设置阈值d2=1.5km，利用用户的OD 坐标信息，补充下车站点后得到的下车站点数据量为1 201 217，占总数据量的85%。

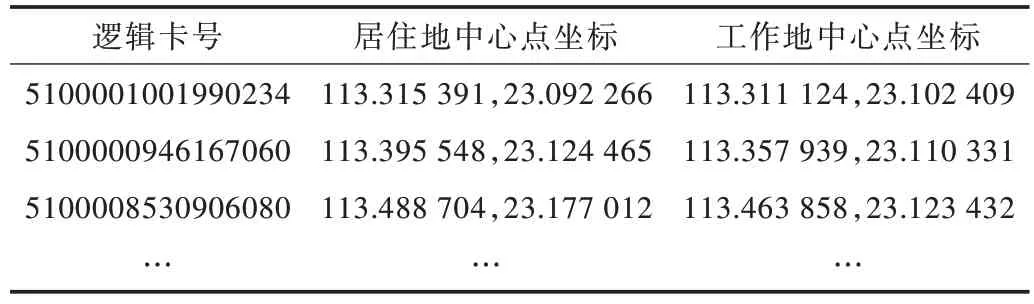
Table 4 User OD coordinate information 1表4 用户OD 坐标信息1

Table 5 User OD coordinate information 2表5 用户OD 坐标信息2

5 结语

本文利用出行链的方式，分析了广州市的公交交易数据和地铁交易数据，对于连续出行的乘客，对本次乘车站点所在线路的下游站点与下次乘车上车站点的距离进行比较，取阈值内距离最小的站点作为下车站点。采用聚类算法进行工作地与居住地计算，使用工作地中心和居住地中心对公交交易数据作进一步补充，实验证明该方法较为有效，准确率高。另外，通过对基于Mean Shift 的公交下车站点判定方法的研究，有助于公交线路优化和公交车辆调度，进一步改善城市公交运营服务，提升居民的公共交通出行效率。