基于聚类分析的汽车行驶工况构建研究

邵云飞，许 冲，胡惠晴

（1.上海理工大学机械工程学院；2.上海理工大学管理学院，上海 200093）

0 引言

汽车行驶工况（Driving Cycle）通常用速度和时间序列表示，可以代表某一区域的行驶行为［1］。汽车行驶工况是量化汽车排放的重要指标，其主要目的是通过模拟真实的驾驶模式来评估汽车的污染排放和油耗。近几十年来，汽车行驶工况一直被用来完成新车的排放认证程序。中国一直采用欧洲排放认证标准测试循环，《世界轻型车测试程序》（World Light Vehicle Test Procedure，WLTP）将取代《新欧洲驾驶循环》（New European Driving Cycle，NEDC）成为新型轻型车排放认证标准测试循环（图1、图2 分别展示了NEDC 行驶工况和WLTC 行驶工况）。然而，随着中国汽车数量的快速增长，近年来中欧之间的驾驶状况差异越来越大。驾驶周期能否充分反映汽车的真实驾驶情况，并提供更准确的估计，越来越受到关注。而且，我国幅员辽阔，各城市道路建设、人口密度及交通状况各异，导致各城市的汽车行驶工况特征具有明显差异。因此，基于城市自身的汽车行驶数据进行城市汽车行驶工况构建研究也越发迫切，希望所构建的汽车行驶工况与该市汽车的行驶情况尽量吻合，理想情况是完全代表该市汽车行驶情况（也可以理解为对实际行驶情况的浓缩）。目前，北京、西安、沈阳等都已经构建了各自城市的汽车行驶工况［2-4］。

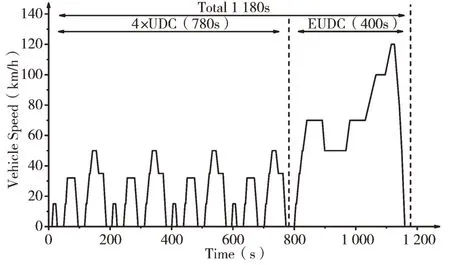
Fig.1 Driving cycle of NEDC图1 NEDC 行驶工况

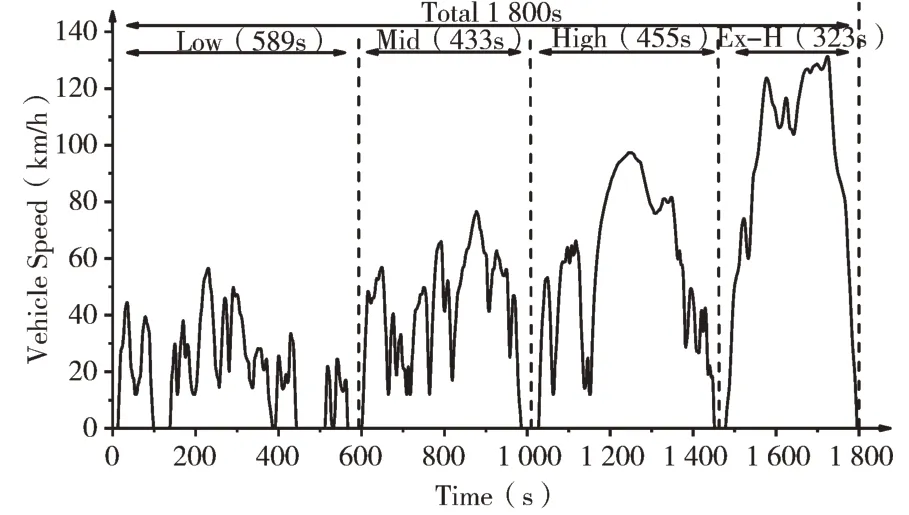
Fig.2 Driving cycle of WLTC图2 WLTC 行驶工况

汽车行驶工况构建本质上属于模式识别在实际工程中的一种应用［5］。目前对于汽车能量管理控制策略的工况识别方法中，主流方法有神经网络［6-7］、聚类分析［8-9］。文献［10］采用神经网络模型进行工况识别，但其特征提取不够全面，模型训练样本较少，且泛化能力较差；文献［11］采用聚类分析法构建了道路汽车行驶工况。文献［12］利用聚类分析方法识别工况，然后基于马尔可夫原理对不同工况进行拼接，构建出代表性工况；文献［13］基于聚类分析法构建出行驶工况，并基于相关系数法对构建的行驶工况进行评价；文献［14］采用聚类分析法构建汽车行驶工况，但未能给出合理的评价体系。

在上述研究背景下，本文根据某城市轻型汽车实际道路行驶采集的数据（采样频率1Hz），基于主成分分析和Kmeans 聚类方法构建汽车行驶工况曲线。首先，基于运动学片段原理对采集到的数据进行划分；然后，选取运行时间、运行速度、平均加速度、怠速时间比、速度的标准偏差等可以描述和评价这些片段的特征参数并进行相应计算，利用主成分分析法对于选取的运动学片段的特征参数进行降维处理，减少计算量；然后将降维以后得到的4 个主成分作为研究变量，利用K-means 聚类对所有运动学片段进行分类，得到3 类代表不同汽车行驶特征的片段，最后提出了基于总体特征参数偏差最小的片段选取方法，对备选工况片段进行筛选，构建出汽车行驶工况图。以原始数据和所构建的行驶工况的特征参数误差作为汽车运动特征评估指标，用来评估所构建的汽车行驶工况的合理性。得到的误差结果越小，说明最终构建出的汽车行驶工况的代表性越强。

1 理论背景

1.1 主成分分析

主成分分析（Principal Component Analysis，PCA）［15］由Pearson 与1901 年第一次提出，用于数据分析及模型建立，它是一种基础的、常用的分析方法。它基于降维理论，将原始的多变量指标经过线性变换，重新组建一组线性无关的综合指标替代原始指标。

给定n个样本，每个样本中含有p个变量，构成一个n×p阶数据矩阵：

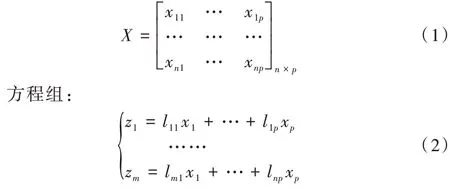
其中，x1,…,xp为原变量指标，z1,…,zm为新变量指标，方程组中系数的确定需满足以下原则：①zi,zj,(i≠j,i,j=1,2,…,m) 相互无关；②z1是x1,…,xp所有线性组合中方差最大的，z2是与z1无关的x1,…,xp的所有线性组合中方差最大的；zm是与z1,…,zm-1均不相关的x1,…,xp所有线性组合中方差最大的，则所组建的新指标z1,…,zm分别是原来变量指标x1,…,xp的第1，第2，…，第m主成分。

1.2 K-means 聚类

K-means 聚类是著名的划分聚类算法，因简洁和高效而得到了广泛应用［16］。K-means 的基本思想是：在给定k值和k个初始聚类簇中心点的情况下，将每个样本点分到离其最近的簇中，之后重新计算每一个簇的中心点（取其平均值），再迭代进行分配点和更新类簇中心点步骤，直至类簇中心点变化很小，或者达到指定的迭代次数。

K-means 聚类的具体计算步骤如下：

（1）首先确定一个k值，即原始数据集经过聚类后得到k个集合。

（2）从原始数据集之间随机选择k个数据点作为聚类中心。

（3）对数据集中的每一个点，计算其与每一个聚类中心的距离（如欧式距离），离哪个聚类中心近，就划分到哪个聚类中心所属的集合。

对于两点之间的距离计算，有以下几种方式：

欧式距离：

（4）将所有数据归好集合后，一共有k个集合，然后重新计算每个集合的中心。

（5）如果新计算出来的聚类中心和原来聚类中心之间的距离小于某一个设置的阈值（表示重新计算的聚类中心的位置变化不大，趋于稳定，或者说收敛），可以认为聚类已经达到期望结果，算法终止。

（6）假如新的聚类中心和原来聚类中心距离变化很大，需要迭代步骤（3）—步骤（5）。

1.3 运动学片段

运动学片段指汽车从怠速状态初始阶段到下一个怠速状态初始阶段之间的行车速度区间，如图3 所示。可以看出，一个相对完整的运动学片段应该包含怠速、加速、匀速和减速阶段。其中，匀速阶段不是必须阶段，因为在一段实际的行驶过程中，可能没有充足的匀速驾驶条件。

Fig.3 Kinematic segment definition图3 运动学片段定义

2 数据采集

本文以某城市的典型道路为对象，采集轻型汽车不同时间段内在实际道路上行驶的数据（包含3 个数据文件，每个数据文件为同一辆车在不同时间段内所采集的数据），采集的部分实验数据所呈现的速度、加速度如图4、图5 所示。

Fig.4 Speed-time diagram of test data图4 实验数据呈现的速度—时间关系

Fig.5 Acceleration-time diagram of test data图5 实验数据所呈现的加速度—时间关系

3 汽车行驶工况构建

3.1 运动学片段划分

一个有效的运动学片段应该包含4 个正常行驶状态，即怠速状态、加速状态、匀速状态和减速状态，且一般不少于30s。汽车的速度—时间曲线通常情况下可以视为由若干个运动学片段组合而成，而汽车在不同交通状况下、不同路线段、不同时间段都会得到不同的运动学片段。利用相应的聚类算法可以将反映相似交通特征的运动学片段进行归类，以此形成几类典型的片段库，再从片段库中挑选最优的片段构建代表性工况。

将试验数据依据运动学片段原理进行划分，得到若干运动学片段。在这些运动学片段中存在一些短时间片段和无效片段，如果不对这些异常片段进行处理，将会导致后续的特征值分析结果出现很大误差，最终导致建立的汽车行驶工况缺乏有效性。因此，如果一个运动学片段的总时长小于30s，则将该片段剔除。

根据上述原则进行运动学片段的划分和筛选后，所得运动学片段数目如表1 所示。部分运动学片段如图6 所示。

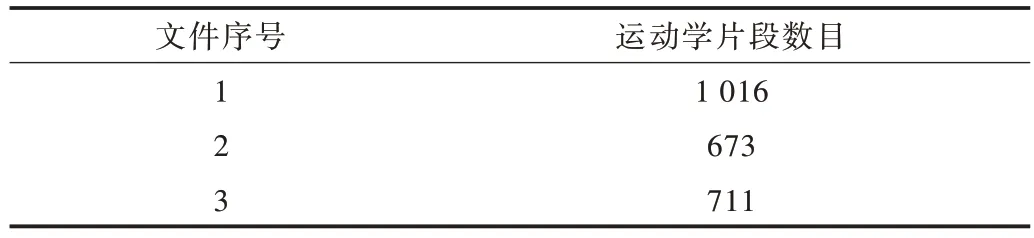
Table 1 Number of kinematic segments表1 运动学片段划分数目

Fig.6 Partial kinematic segment图6 部分运动学片段

3.2 运动学片段特征提取

每一个运动学片段都包含了若干个速度—时间点，每个运动学片段也都有各自的运动学特征。工况构建是从每一类运动学片段库中，按照特定的选取规则挑选出符合要求的候选片段，然后进行组合拼接形成最终工况。要描述和评价一个运动学片段，需要选取相应的运动学特征参数，这些运动学特征参数能够尽可能全面地将运动学片段根据其运行状态进行描述并形成基于运动学片段的数学模型。挑选适宜的运动学片段构建汽车行驶工况以及对所构建的代表性汽车行驶工况进行评价有其基本准则可行。为了便于运动学片段分类，本文将运行时间、运行速度、平均加速度、怠速时间比、速度的标准偏差等18 个运动学片段特征参数作为评价指标。表2 是本文选择的运动学片段特征参数以及它们的符号表示。计算出汽车行驶数据处理后得到的2 400 个运动学片段中每个片段的特征参数值，得到的特征值矩阵如表3 所示。

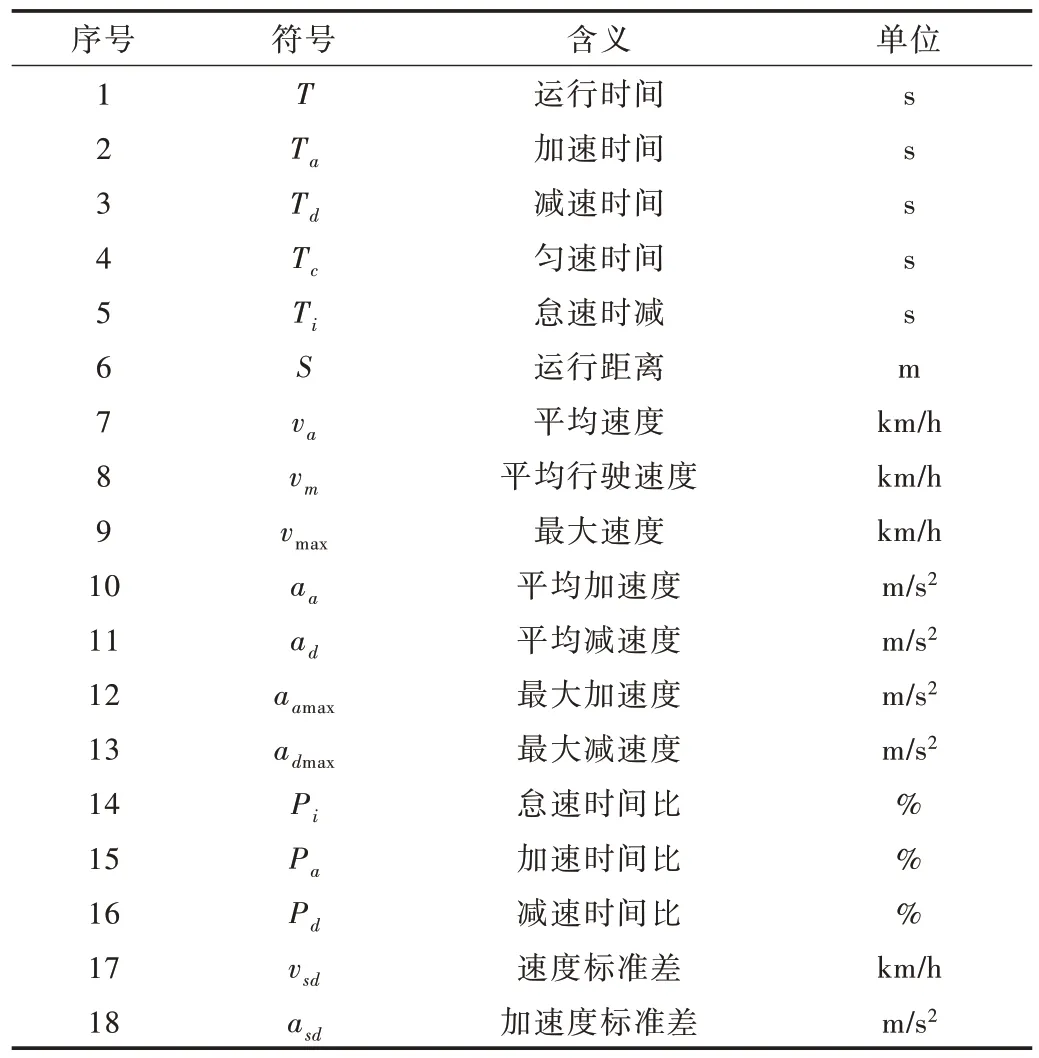
Table 2 Characteristic parameters of kinematic segments表2 运动学片段的特征参数

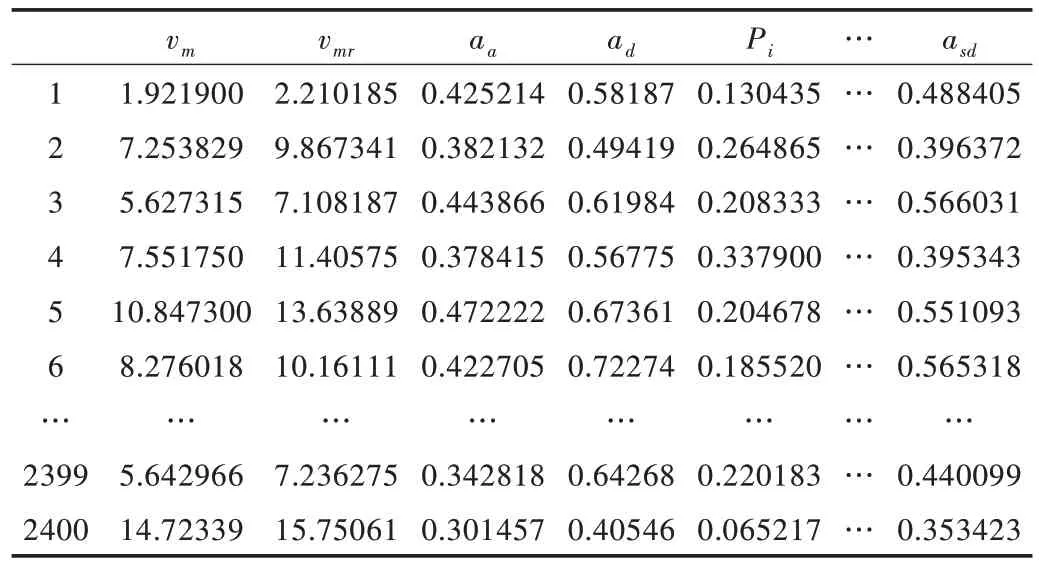
Table 3 Kinematic segment eigenvalue matrix表3 运动学片段特征值矩阵

3.3 主成分分析降维

基于主成分分析原理，给出主成分分析对于数据的计算步骤，如下：

（1）首先对变量进行标准化处理，去除量纲影响，即：

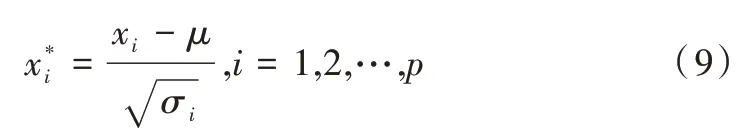
其中，μ=E(xi),σi=Var(xi)。

（3）计算特征值和特征向量，利用|λI-R|=0 求解，并将得到的特征值按照其大小进行排列，然后分别求出它们对应的正交化特征向量ei，满足‖ei‖=1。

（4）建立回归方程计算贡献率，当累积贡献率达到一定百分比时，则认为这些主成分可以综合表示所有指标所要表达的信息，从而达到降维目的。

贡献率这一指标指第i个主成分的方差在全部成分方差中所占比重；累计贡献率指前i个主成分的综合能力，用描述。

（5）提取出主成分，计算每一个主成分的得分。

根据上述定义，经程序计算得到各主成分的特征参数值、贡献率和累计贡献率，如表4 所示。

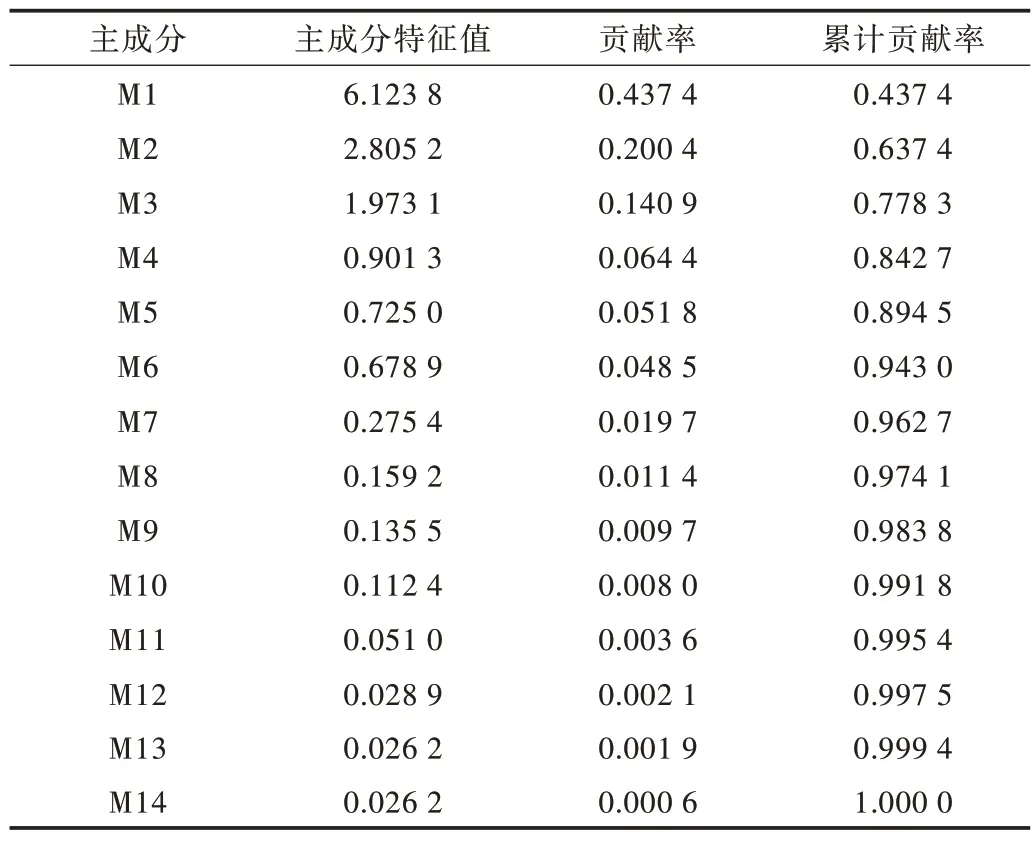
Table 4 Principal component contribution rate and cumulative contribution rate表4 主成分贡献率及累计贡献率

由主成分分析法的原理可知，主成分特征值的大小表示该主成分反映原来特征参数能力的大小，特征值越大，表明该主成分能较大程度地替代原始变量。贡献率代表一次性表示原来多个特征参数所反映信息量的能力，贡献率越高，说明该主成分能反映特征参数的数目越多。在本文中，当累计贡献率超过80% 时，即可认为这几个主成分能够完全反映原理所有的特征参数。从表4 可以看出，前4 个主成分的累计贡献率已达到80%，因此将这4 个主成分当作运动学片段新的特征，能够大大减少计算量。经主成分分析计算后还得到了一个主成分载荷矩阵，该矩阵中的每一列元素都是原来特征参数与该列所代表的主成分的相关程度，数越大代表该特征与主成分关系越紧，能很大程度地反映主成分的信息量。前4 个主成分的载荷矩阵（主成分系数矩阵）如表5 所示。

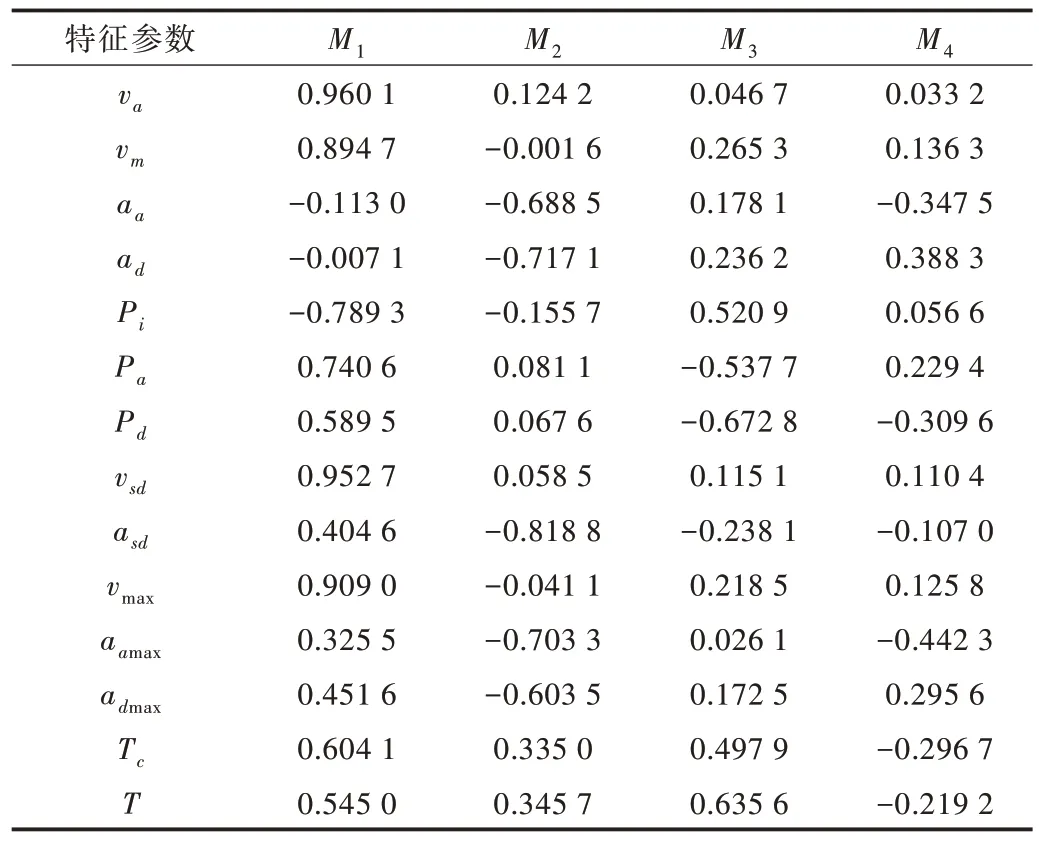
Table 5 Component load matrix表5 主成分载荷矩阵

从表5 可以看出，第1 个主成分主要反映了平均速度、平均行驶速度、怠速时间比、加速时间比、减速时间比、速度标准差、最大速度、匀速时间共8 个特征参数；第2 个主成分反映了平均加速度、平均减速度、加速度标准差、最大加速度、最大减速度共5 个特征参数；第3 个主成分反映了怠速时间比、加速时间比、减速时间比、片段总时间共4 个参数；第4 个主成分主要反映了平均减速度、最大加速度2 个特征参数。还可以得出，这4 个主成分能够全部反映本文所列的运动学片段的所有特征参数，将主成分载荷系数矩阵与标准化后的样本数据矩阵相乘即可得到运动学片段的主成分得分矩阵。在此，本文选取前4 个主成分的得分值作为K-means 聚类的研究变量。

3.4 K 均值聚类分析

利用K-means 聚类法对由主成分分析最终得到的4个主成分得分矩阵进行分类，2 400 个运动学片段被分为3类：第1 类有1 234 个片段，第2 类有980 个片段，第3 类有186 个片段。计算每一类总的特征参数，以便更好判断处于该类情形下的汽车行驶状态，如表6 所示。

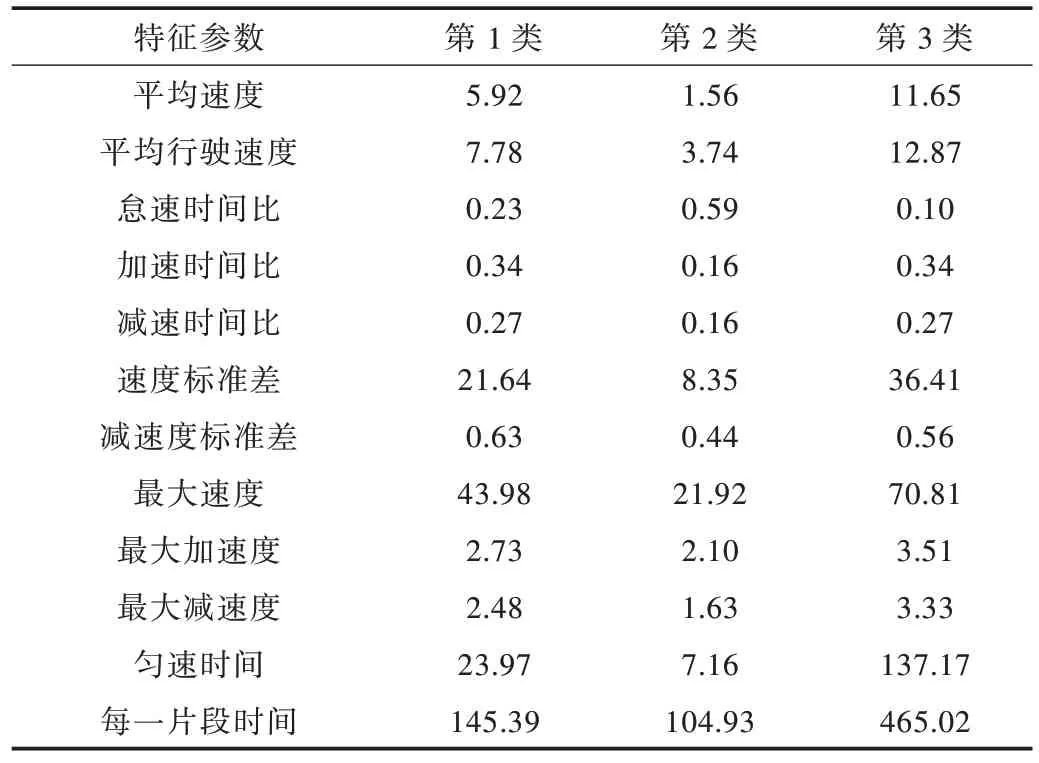
Table 6 Comprehensive characteristic parameters of each class表6 各类综合特征参数

每一个特征参数都或多或少可以反映该车运行状态，在第1 类中，各特征参数大都处于比较中间的区间，可判断该车处于相对中速情况中；在第2 类中，怠速时间比是3类中最大的，但平均速度最低，最大加速度和最小减速度也是这种情况，说明汽车一直进行加减速操作，可判断该车处于频繁堵车的实际路况中，是低速情况；在第3 类中，平均速度相对最高，且匀速行驶时间最长，说明道路比较畅通，汽车处于相对高速状况。

通过以上简单分析，可以大致了解到此辆汽车大多数情况下都处于较低速度状态，通过主成分分析法得到的主成分可以使分类过程简化、效率提高，分类效果也较理想。

3.5 代表性行驶工况构建

将运动学片段分好类后，还要构建最终的行驶工况曲线，其目的是尽可能真实地反映汽车在不同情况下的行驶状况。由于每一类片段包含了一种或几种特征参数，若从每一类片段中挑选若干个片段，再组合起来，就能构建出符合要求的工况曲线，因此有必要选择合理的片段挑选方法，这关系到所构建工况的准确程度。

常用的选取方法有随机选择法［17］、最佳增量法［18］、VA 矩阵法［19］、小波变换法［20］等，随机法思路简单，挑选的片段具有随机性，组合后误差难以保证；最佳增量法在进行比较时，步骤繁琐，计算量较大；V-A 矩阵法通过联合概率密度分布矩阵挑选相关性最大的片段；小波变换法使用场景受限，但处理效果好。每种方法都有其适用范围和限制，本文采用基于总体特征参数偏差最小的片段选取方法，该方法科学合理，易于以程序实现。最终构建的汽车行驶工况如图7 所示。

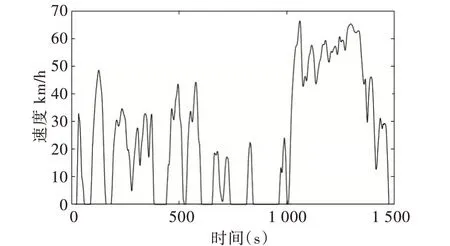
Fig.7 Curve of final driving cycle图7 最终行驶工况曲线

4 汽车行驶工况评价

工况组合后，要判断所构建的汽车行驶工况是否合理，只需要将构造前的运动学片段总的特征参数与构造好的工况曲线的特征参数进行相应比较，并计算两者之间的相对误差，才能对构造的好坏有量值评价，构建前后各特征参数及误差如表7 所示。

可以清楚看出，实验数据和构建工况的特征参数之间差异很小，而且误差都在8% 以内，说明构建的行驶工况比较合理，能够较为全面地反映该城市实际道路行驶状况。

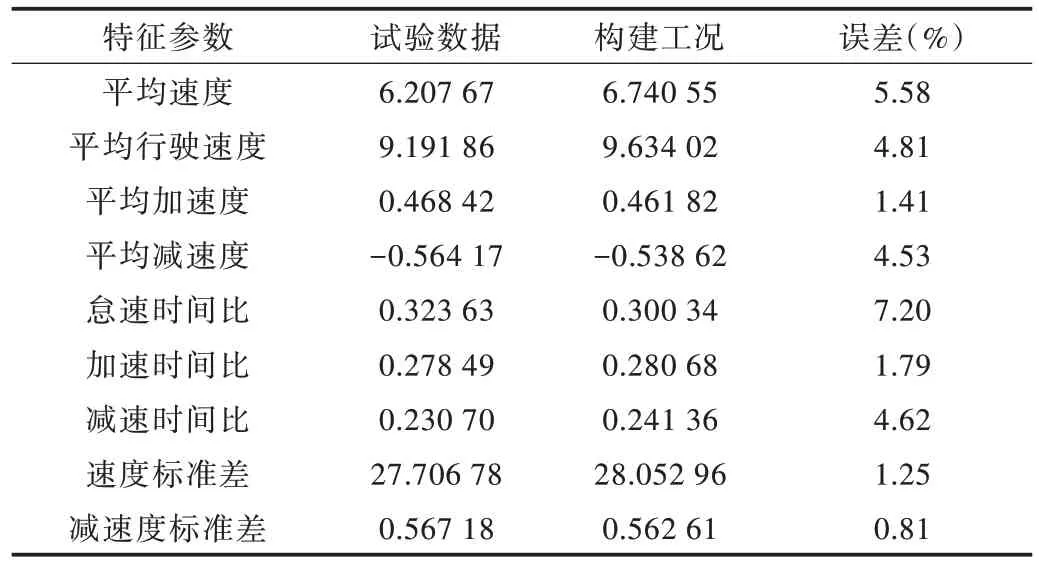
Table 7 Characteristic parameter and error before and after construction表7 构建前后各特征参数及误差

5 结语

本文以所得轻型汽车实际道路行驶数据为例，将大量行驶工况的数据划分为运动学片段，选出18 个特征参数进行研究。首先基于主成分分析法对运动学片段特征参数进行降维处理，然后利用K-means 聚类方法对其进行分类，最后基于总体特征参数偏差最小的片段选取方法，在构建出一条具有代表性的行驶工况曲线的同时，形成一个完善的汽车运动特征评价体系。

分析结果表明，本文利用城市汽车行驶数据进行行驶工况的构建研究，所使用的模型可靠便捷，所构建曲线与实际工况具有较高的吻合度，在保证计算准确度的同时具有一定科学价值，可为后续研究提供良好思路。