基于DCPSO 算法的微网系统优化调度

徐远志，张会林，赵星虎

（上海理工大学机械工程学院，上海 200093）

0 引言

环境和能源问题越来越严重，为解决传统能源弊端，各种灵活的分布式能源（Distributed Energy，DE）得到快速发展。微电网是一个包含分布式电源、储能装置和能量转换装置的小型独立系统，可以独立运行，也可以并入电网运行［1-4］。微网通过协调系统各微源的出力使系统安全经济运行，保证系统稳定性［5-8］。通过合理规划微源出力使系统在不同负荷情况下安全运行是微网优化调度研究重点［9］。

微网优化调度研究成果有：文献［10］提出一种自适应人工鱼群算法，以微网系统在分时间电价下的经济性作为目标对系统进行优化调度，但没有考虑风光等不稳定发电方式对系统的影响；文献［11］建立优化微网经济、环境的调度模型，提出一种蜂群搜索策略的改进量子粒子群算法，具有较强的全局搜索能力和精度，但缺少风光等分布式电源模型；文献［12］以运行成本、环境成本建立微网优化调度模型，系统包含风电等分布式电源，提出一种布谷鸟算法与快速非支配排序遗传算法融合的改进算法，但在建立模型时未考虑机组的投资成本；文献［13］以系统总成本最小为目标函数，应用遗传算法和微网能量管理策略，对微网系统规模进行优化；文献［14］提出一种考虑EV 响应的光储微电网储能优化配置，建立技术接受度模型，可使微网系统电能损失减少，提高系统整体收益，但未考虑风光电源的不稳定性对优化结果造成一定的偏差；文献［15］提出一种结合粒子群算法和差分进化算法的双种群混合算法，对热电联共系统进行经济优化调度，结果证实算法的先进性，但算法未考虑种群初始化时粒子分布不均问题。

本文在前人研究基础上进行改进，建立含风机（Wind Turbine，WT）、光伏电池（Photovoltaic，PV）、燃料电池（Fuel Cell，FC）、微型燃气轮机（Micro Turbine，MT）、储能电池（Energy Storage Battery，ESB）和负载等微源的微网系统，综合考虑系统成本、环保等因素，建立目标函数。对普通粒子群算法进行改进，提出双种群混沌粒子群算法。通过算例求解验证所提算法具有更快的收敛速度和更好的寻优能力，证明改进算法具有先进性。

1 微网各单元模型

本文研究的微网系统包括光伏发电、风力发电、储能发电、燃气发电等分布式发电方式，微网系统结构如图1所示，各分布式电源通过公共连接点与大电网相连。

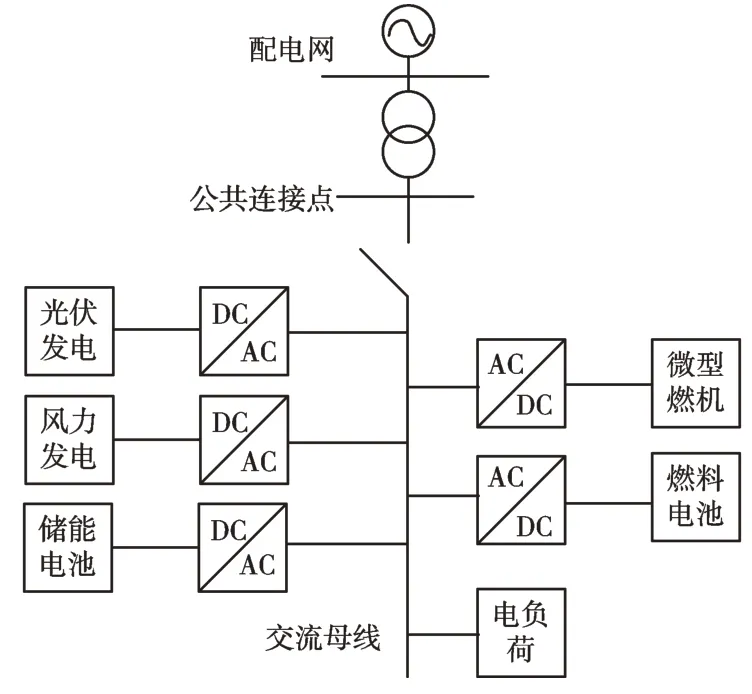
Fig.1 Microgrid system structure图1 微网系统结构

1.1 光伏发电

光伏发电功率与温度和光强有关，当温度为25℃、光照强度为1 000W/m2时，在标准测试条件下可近似求出光伏阵列输出功率，见式（1）。

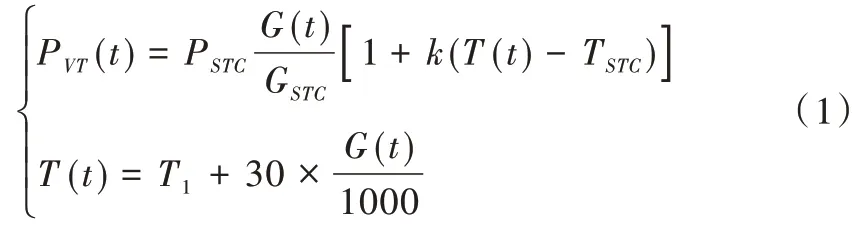
式（1）中，P(t) 为光强为G(t) 时的输出功率，GSTC为标准测试条件下的光强，PSTC为标准测试条件下的最大输出功率，k 为功率温度系数，T(t) 为t 时的表面温度，可通过环境温度T1和光照强度G(t)求出。

1.2 风力发电

风力发电机组输出功率与风速相关，其输出功率的概率密度可近似由式（2）表示［16］。

式（2）中，k为形状系数，v为风速，c为尺寸系数。输出功率可表示为：

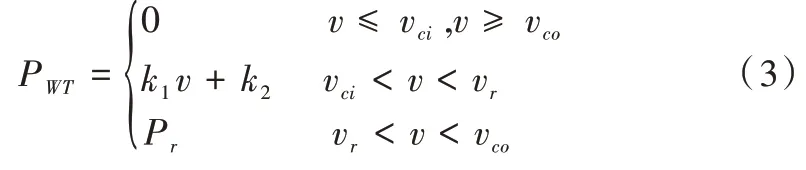
式（3）中，Pr、vr为风机的额定输出功率和风速，vci、vco为切入、切出风速。

1.3 微型燃气轮机

作为一种小型的热力发电机，其功率范围一般在25～300kW。燃料成本取决于发电量和发电效率，功率大小具有可控性［17］。燃料成本数学模型表示如下：

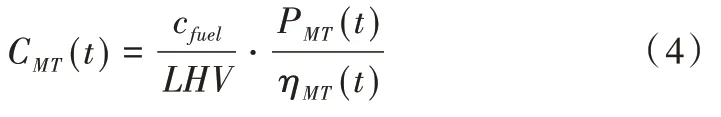
式（4）中，CMT(t) 为t 时段燃料成本，PMT(t)、ηMT(t) 为燃气轮机在t 时间段内的输出功率和效率，天然气低热值量LHV本文取9.7kWh/m3，天然气价格本文取2.5元

1.4 燃料电池

燃料电池在工作过程中发电效率比较高，能将化学能转换为电能，燃料电池成本可表示为：

式（5）中，CFC(t) 为时间段t 内持续保持燃烧的费用，PFC(t)、ηFC(t) 分别为t 时间段燃烧的输出功率和t 时间段系统燃料转换为电能的效率。

1.5 储能电池

储能电池在微网中能够根据其它微源的出力情况进行调节以保证微电网平稳运行。荷电状态（State Of Charge，SOC）数学模型可表示为：

式（6）中，SOC(t)、PES(t) 分别代表t 时段储能电池的荷电状态和充放电功率，PES(t) 值为正时代表放电，为负时代表充电，CES代表储能电池的容量，ηd、ηc代表储能电池的放电效率和充电效率，Δt为时间间隔［18］。

2 微网多目标优化模型

2.1 目标函数

微网容量优化配置主要考虑在满足负荷需求前提下对微网分布式能源合理分配，实现微网经济最大化、环境污染最小、安全性最高的目标。

目标函数F 包括投资、运行和维护成本F1，环境影响成本F2和大电网交易成本F3。

（1）运行成本F1可用以下数学模型表示：

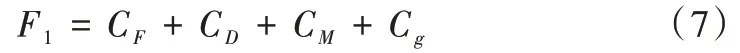
式（7）中，CF、CD、CM、Cg为燃料、折旧、维护及交易成本，每种成本计算公式如下：

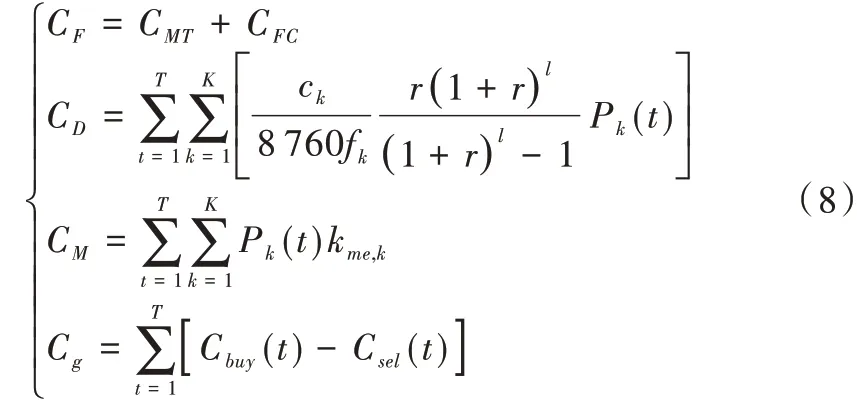
式（8）中，ck、fk、kme,k分别表示分布式电源k 的安装成本、容量系数、维护成本系数，r和l表示年利率和分布式电源寿命年限，式中Pk代表输出功率。

（2）环境成本F2主要包含系统产生的SO2、CO、NOx等有毒有害气体污染处理费用，其治理成本表达式如下：

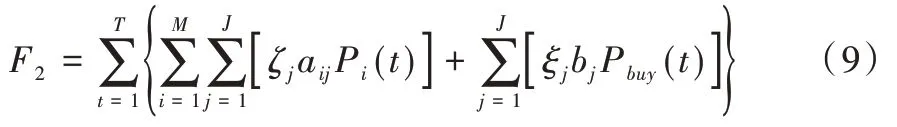
式（9）中，M 和J 分别代表排放污染气体分布式电源种类数目和污染气体种类数目，ξj为第j种气体的污染系数，aij、bj分别代表第j种气体在第i种分布式电源运行时排放系数和大电网运行时排放系数，Pbuy(t)、Pi(t) 为t 时刻的购电量和t 时刻微源i的发电量。

（3）大电网交易成本F3。微网与大电网交易成本表示如下：

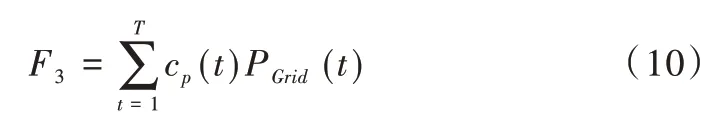
式（10）中，cp(t) 代表t 时段电网购售电价格，PGrid(t) 为t 时段微网与大电网的交互功率。

2.2 约束条件

（1）功率平衡约束。

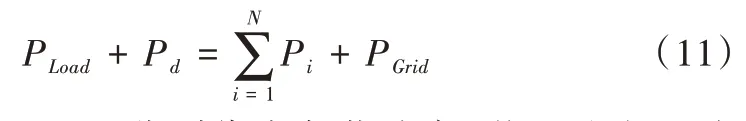
式（11）中，PLoad、Pd分别代表负荷功率、蓄电池充电功率，Pi代表分布式电源输出功率，N 代表分布式电源个数，PGrid代表购电量。

（2）分布式电源出力约束。

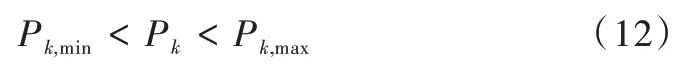
式（12）中，Pk,max和Pk,min代表电源k的功率上下限值。

（3）交换功率约束。

式（13）中，PGrid(t) 代表t 时刻微网和主网间的能量传输值，PGrid,min(t)、PGrid,max(t) 代表t 时刻微网和主网的交互功率大小限值。

（4）储能电池功率约束。

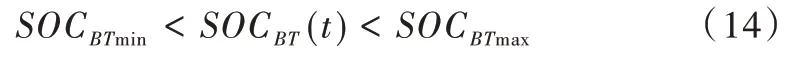
式（14）中，SOCBT(t) 代表储能电池所带的电荷量，SOCBT,max、SOCBT,min分别为功率上下限。

3 算法

3.1 标准的粒子群算法

粒子群算法是一种根据鸟类寻找食物路径规划启发创立的智能优化算法，群体中每个个体称为粒子，它的基本思想是通过更新粒子位置不断寻优直到最终找到最优解［19-20］。假设在一个D 维空间中，粒子i的位置是xi，速度是vi，其位置和速度更新公式如下：

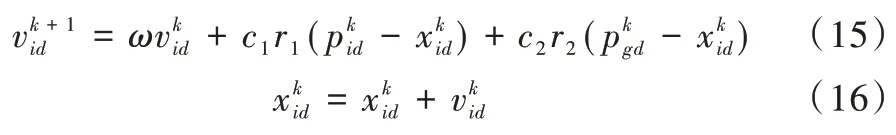
式中，vid、xid代表粒子的速率和位置；ω为惯性权重，用于调节粒子搜索空间，值越小，粒子越趋于局部最优，值越大，粒子越趋于全局最优；pi、pg为个体最优和种群最优；r1、r2为0-1 的随机数；c1、c2为学习因子，用于调节粒子全局最优和局部最优搜索权重；k为迭代次数。

3.2 改进粒子群算法

3.2.1 惯性权重线性下降

基本粒子群算法存在易于陷入局部最优，引入惯性权重线性下降粒子，依据迭代次数线性调整惯性权重ω的大小。迭代初期，增大ω，扩大粒子搜索范围，以免陷入局部最优解，加速搜索速度；迭代后期，逐渐减小ω，缩小搜索空间，有利于种群收敛。惯性权重下降法从时间角度改进粒子群算法，解决种群搜索空间小和不易收敛的矛盾。改进的惯性权重公式如下：

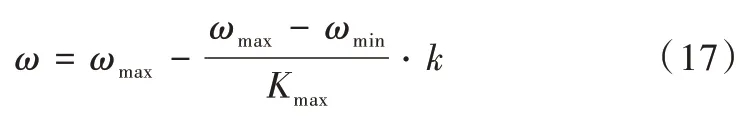
式（17）中，k、Kmax为当前迭代次数、最大迭代次数；ωmax、ωmin为惯性因子上下限。

3.2.2 双种群粒子改进

传统PSO 算法结合实际问题优化时，不可避免会产生早熟、陷入局部最优解问题。为了协调种群扩大搜索空间和加快收敛，将传统粒子群分为两个互补种群联合优化。

第一种群优化公式如下：

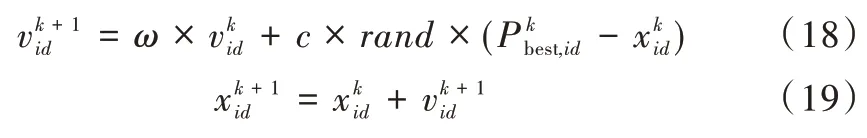
第二种群优化公式如下：

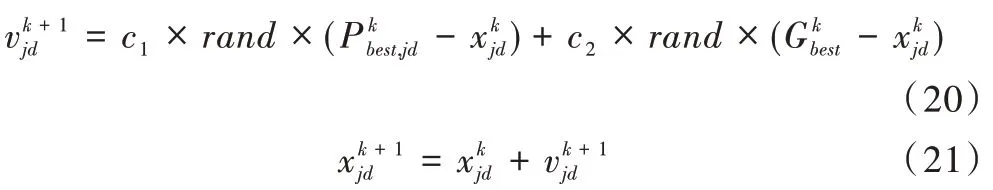
两个种群通过迭代共享机制共享全局最优。种群一不含全局最优因素，迭代过程不参考全局最优，搜索空间更大，不会陷入局部最优；种群二搜索空间更小，收敛速度更快，提升了种群收敛性。两个种群协同互补运行，从空间上分为互补种群，解决传统粒子群算法收敛精度低、不易收敛的问题。

3.2.3 混沌映射粒子改进

传统粒子群算法在初始化及迭代过程中粒子分布不均匀。为提高种群初始化均匀度，扩大种群更新路径，引入混沌优化改进粒子群算法。

当系统处于混沌状态时，可在空间范围内进行不重复的无规则运动，采取非线性往复运动进行控制，可较为容易地扩大系统空间，提高系统均匀度。混沌优化算法可用Logistic 方程表示如下：

式（22）中，∂为混沌系统控制系数，xn、xn+1为系统当前和下一状态值。

3.3 算法描述

将上述3 种改进方法结合，对传统粒子群算法进行改进，解决传统粒子群算法收敛速度慢、精度低、初始化不均匀和易陷入局部最优等问题。具体步骤如下：①初始化参数、种群数和初始惯性权重；②初始化种群，计算粒子位置和速度；③归一化初始种群，进行种群混沌处理，反归一化；④计算两种群对应适应度值，并找到个体最优和全局最优值；⑤更新双种群粒子位置和速度；⑥判断是否满足输出条件，否则归一化迭代粒子，进行种群迭代过程混沌处理，反归一化。

改进的算法流程如图2 所示。

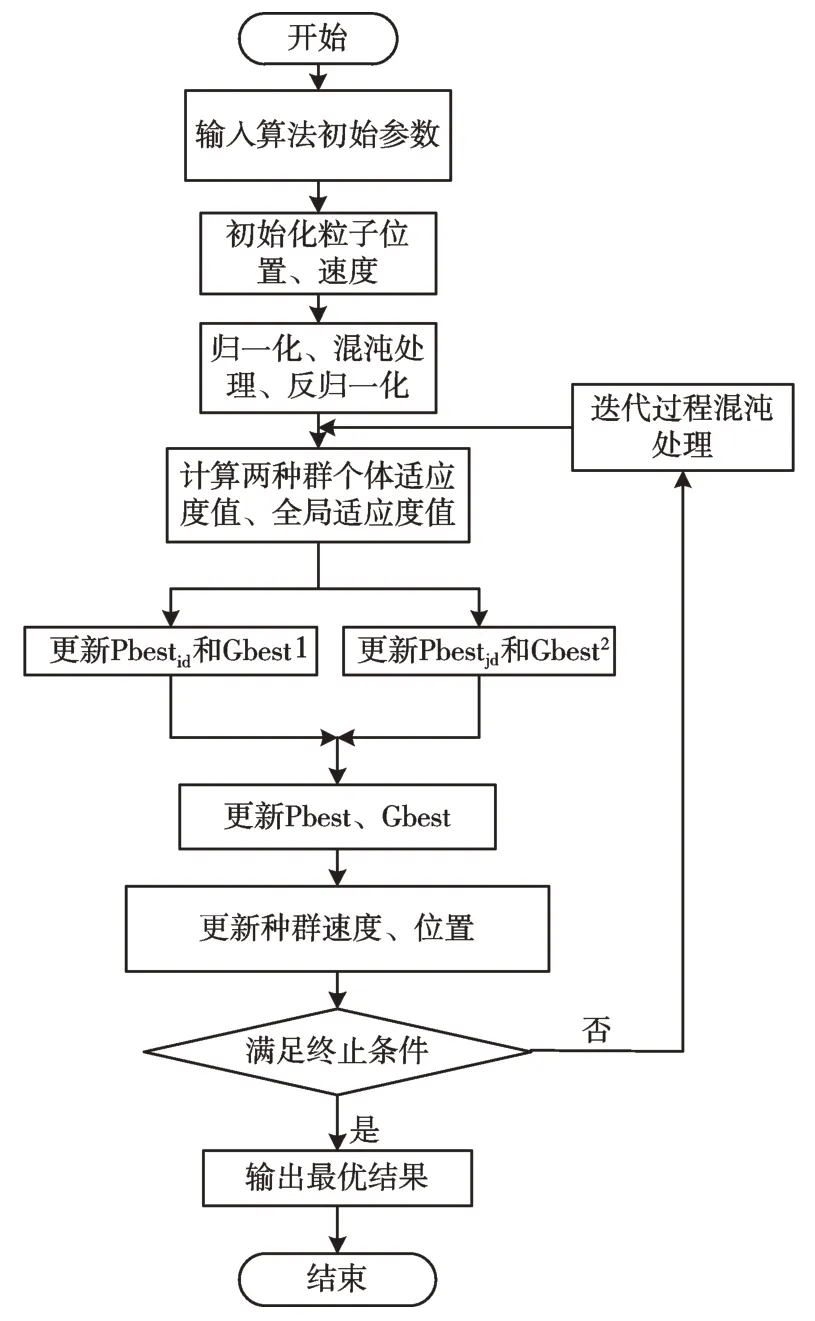
Fig.2 Flow of double-population chaotic particle swarm optimization algorithm图2 双种群混沌粒子群算法流程

4 算例分析

本文对某地区微网系统进行研究。微网优化调度以每小时为一个时段将一天划分为24 个时段。设各微源使用年限为15 年。表1 为几种微源的容量、装机成本和维护成本系数。图3、图4 为该地的典型日负荷功率曲线和单台风机光伏发电出力图。微网购售电价格如表2 所示。

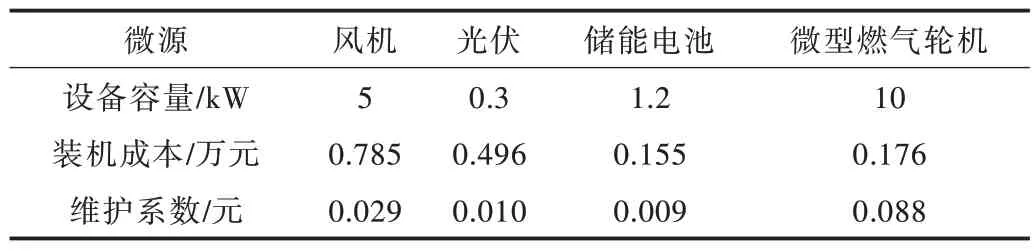
Table 1 Correlation coefficient of micro-source表1 微源相关系数

Fig.3 Daily load power curve图3 日负荷功率曲线

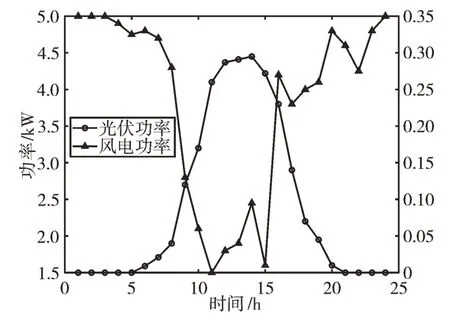
Fig.4 Output curve of fan and photovoltaic cell图4 风机和光伏电池出力曲线

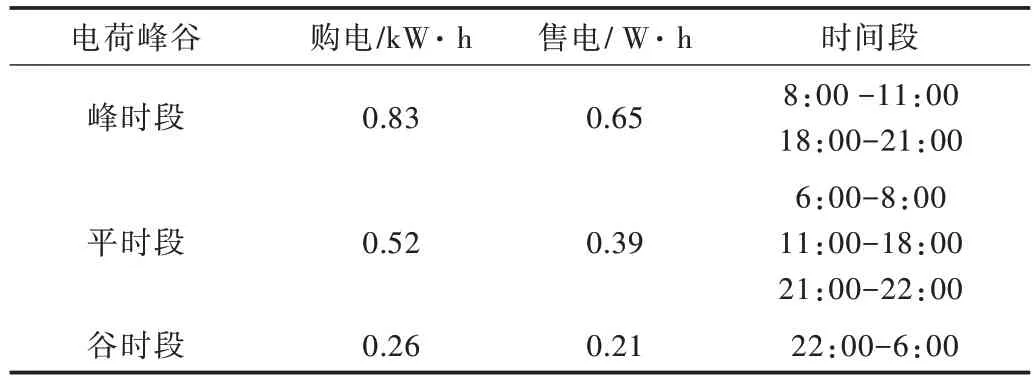
Table 2 Purchase and sale price of microgrid electricity（Yuan/kW·h）表2 微电网购售电价格元/kW·h

风光发电作为清洁能源，没有燃料成本和环境成本，在微网系统中会优先消耗。微型燃气轮机和燃料电池在使用过程中会产生污染气体。对于在发电过程中微电网系统所产生的污染物需进行处理，处理这些污染物所需费用如表3 所示。

Table 3 Relevant parameters of pollutant treatment表3 污染物处理相关参数

分别采用传统的粒子群算法和改进的粒子群算法进行优化调度，相关参数设置如下：学习因子c1、c2取1.2，惯性权重系数ωmin、ωmax分别为0.4 和0.9，种群数目N 取100，进行200 次迭代，得到优化后的系统各微源出力如图5、图6 所示。两种算法运行成本如表4 所示。

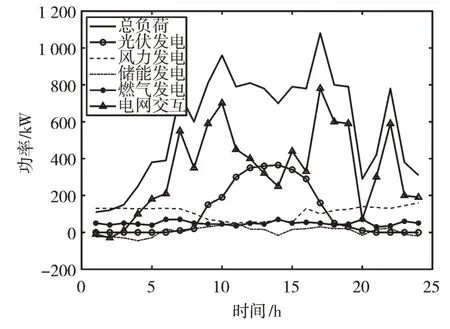
Fig.5 Output of micro-sources in microgrid after MOPSO optimization图5 MOPSO 优化后微网各微源出力

Fig.6 Output of micro-sources in microgrid after DCPSO optimization图6 DCPSO 优化后微网各微源出力

Table 4 Operating costs under different algorithms表4 不同算法下的运行成本

从图5、图6 的优化配置结果可知，使用改进后的粒子群算法更具经济性。采用双种群混沌粒子群进行优化时，微网系统与电网交互功率更加平缓，峰值降低。在电价较低的谷时段风电出力较多。由于电价较低，燃气发电此时保持最小功率，不足的负荷部分向电网购电。在负荷高峰时间段，系统向大电网售电，此时保持燃气发电工作在最大功率。在平时段，优先消耗风光发电，此时燃料电池发电成本较高，负荷功率由电网购电供给。储能电池选择在电价低时充电，电价高时放电。此外，频繁给储能电池充放电会对电池造成伤害。相较于图5，改进后的算法优化方案配置中，储能电池的SOC 值较高，提高了等效充电次数，避免过度充放电，提高了电池使用寿命，降低了系统成本。

由表4 可知，本文提出的双种群混沌粒子群算法相比一般粒子群算法更具经济性，具有更快的收敛速度，在投资、维护和环境成本方面分别减少8.43%、2.11% 和14.69%，验证了本文改进算法的经济性和实用性。

5 结语

本文对包含多种分布式电源和储能电池的微网系统进行优化调度。首先对各分布式电源和储能电池模型进行分析，建立一个包含运行成本、环境成本和电网交互成本的目标函数。以各微源出力作为约束条件，采用改进后的双种群混沌粒子群算法求解调度模型。调度结果表明，改进后的算法提升了原算法的收敛速度，精度也得到提高，具有先进性。本研究合理规划微网系统各微源出力，降低了用电运行成本，电力用户可根据所提方案获得更好的经济效益。

本文未考虑风光负荷预测误差，建立准确的风光负荷预测误差模型是下一步研究重点。