改进粒子群优化的多类LS-SVM电机故障识别算法
2021-04-23郭香蓉王世峰
陈 义,郭香蓉,王世峰
(1.湖南工业职业技术学院汽车工程学院,湖南长沙 410208;2.长沙理工大学电气与信息工程学院,湖南长沙 410004)
0 引言
电机故障可能由多种故障机制引起,其中电机结构与运行状态等参数对其诊断有显著影响。传统电机故障诊断基于单一参数、单一特征,并且由于环境等因素,存在很大不确定性,难以满足灵敏度和准确度的要求[1-4]。
近年来,人工神经网络、模糊数学、聚类原理和灰色系统理论被用于电机故障诊断[5-6]。Vapnik 在1995 年基于统计学理论中的VC 维理论与结构风险最小原理,提出支持向量机(SVM)理论,该理论已成为机器学习领域研究重点,且应用广泛[7-8];Suykens 等[9-10]提出的最小二乘支持向量机(LS-SVM)训练简单且收敛快,但在实际应用过程中,矩阵需要进行求逆运算,很难将其应用于高维问题。可采用粒子群优化算法求解高维线性方程组,从而避免矩阵求逆。
本文在粒子群优化算法、LS-SVM 基础上,提出一种基于改进粒子群优化算法的多类LS-SVM 电机故障识别算法,利用该算法对800 组数据进行处理,并与采用标准粒子群优化算法的LS-SVM 进行比较,证明该算法有效性。
1 算法改进
1.1 改进粒子群算法
Kennedy 等[11]对自然界鸟群捕食行为进行研究,提出粒子群优化算法(Particle Swarm Optimization,PSO),即基于当前最优粒子在解空间中搜索粒子,种群中的个体以合作和信息共享的方式搜索最优解,粒子位置表示问题空间的1 个基本解。算法描述如下:
在N维空间中有m个粒子,设xi=(xi1,xi2,…,xin)表示第i个粒子的位置,vi=(vi1,vi2,…,vin)表示第i个粒子的当前速度;pi=(pi1,pi2,…,pin)表示第i个粒子经历的最好位置,为群体中所有微粒经历的最好位置。对于第k代,第i个粒子速度和位置根据式(1)—式(3)进行进化。

其中,k、k+1 分别表示当前迭代次数,w为惯性权重,φ1和φ2是加速度常数,代表每个粒子向pi和pg位置运动的统计加速项权重。其中,如果加速度常数较低,则允许粒子徘徊在最优解附近,收敛速度慢,精度较低;如果加速度常数较大,则粒子可以较快速度逼近最优解,甚至越过最优解,导致算法不收敛[12-13]。通常取φ1=φ2=2,rand1和rand2为两个在[0,1]范围内变化的随机数,vmax为最大速度。因此,本文提出依据粒子适应度优劣调整惯性权重w,即在算法初始阶段,赋予w一个较大的正值,以得到较快的收敛速度,确定最优解区域;在算法后半部分,为使算法更容易收敛、精度更高,赋予w较小的值。其具体方法为:

其中,wmax为搜索开始时最大的w,设为0.91;wmin为搜索结束时最小的w,设为0.39;k为当前迭代步数,K为最大迭代步数。其中w随算法迭代线性减少,使开始时搜索较大的区域,较快确定最优解大致位置;随着w逐渐减小,粒子开始降低搜索速度,展开局部精准搜索。
(2)当f(xi)<f,粒子应该是种群中相对较优的粒子,理论上接近全局最优。因此,粒子被赋予1 个小的惯性权重,以加速粒子整体最优收敛。依据粒子适应值调整w惯性权重。
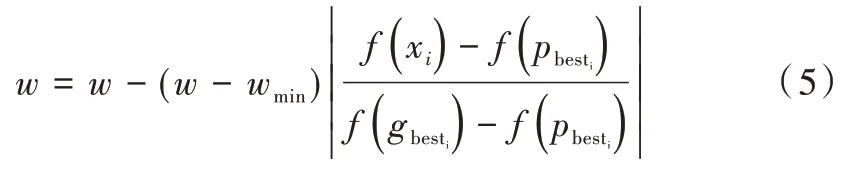
其中,wmin为w的最小值,本文取wmin=0.39。粒子适应度越优,其惯性权重w越小,有利于局部寻优。
1.2 基于改进粒子群优化算法的LS-SVM 求解
给定训练样本集S=其中xi∈Rn、yi∈R分别为输入、输出数据,LS-SVM 利用SRM准则,寻找权向量w和偏差量b,即最小化目标函数为:
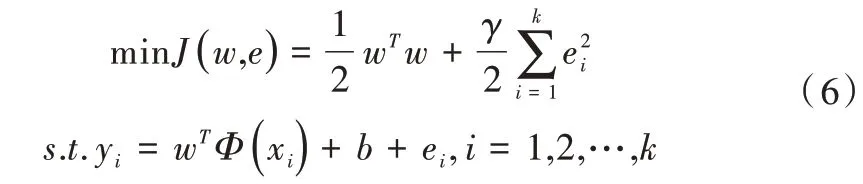
其中,w为权重向量,γ为常数,b为常值偏差。
定义Lagrange 函数求解上述优化问题。

由式(9)可知,求解j=需对A求逆。然而,实际工程通常是高维问题,矩阵求逆运算计算量大且效率低,难以应用。为此,可采用改进的粒子群优化算法,根据迭代计算求解矩阵方程。其算法流程如下:
(1)初始化粒子群。设定粒子群参数,在N维空间中随机产生m个粒子x1,x2,…,xm,组成初始种群X(t);随机产生各粒子xi的初始速度vi1,vi2,…,vin,组成速度矩阵V(t);每个粒子个体最优解初始值为xi的初始值。
(2)评价各粒子适用度(fitness)。在具体矩阵方程求解中,可按(z-Aj)的均方差定义适应度函数。
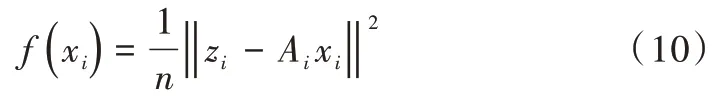
(3)对所有粒子,比较当前适应度f(xi)和历史最好位置适应度=xi,并根据式(4)调整w;比较群体所有粒子当前适应度f(xi)和群体最好位置适应度then 全局最优解并根据式(5)调整w。
(4)更迭粒子位置和速度,产生新的粒子种群X(k+1),速度调整规则为:

(5)检查结束条件。若满足条件,则结束粒子寻优,返回结果为当前的最优个体;否则k=k+1,转至步骤(2)。如果迭代到最大迭代次数kmax,或者适应度函数值小于给定精度,则结束迭代。
1.3 多类LS-SVM
传统LS-SVM 主要用于2 值分类问题,对于多值分类问题,主要有一对一、一对余等方法[14-15]。其中一对一的分类算法类似于投票法,会出现不同类别的票数相当但不可分的情况,而且对于N 值分类问题必须训练N(N-1)/2个分类器,结构庞大,分类效率低。因此可采用一对余的方法。电机故障主要集中在4 个部位,有定子故障、转子故障、轴承故障、轴故障,所以需4 个LS-SVM 分类器。首先判断是否为1 类故障(定子故障),如果是,则结束对该样本的判断,继续下一个样本;否则判断是否为2 类故障(转子故障),直至第4 类故障(轴故障)判断完毕。其结构如图1 所示。
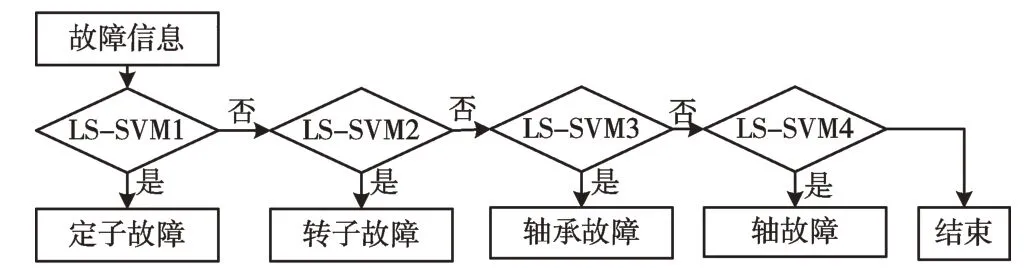
Fig.1 The structure of one-against-rest LS-SVM classifier图1 一对余LS-SVM 分类结构
2 实验结果
为检验本文提出的基于改进粒子群优化的多类LSSVM 电机故障诊断模型应用效果,进行实例分析。本文搜集了已确定实际故障结果的800 组典型电机故障分析记录,将这些记录分为2 部分,前400 组作训练样本,后400组作测试样本。
(1)信息归一化处理。电机故障时,将有不平衡的气隙电压和线电流、扭矩脉动增大、平均扭矩减小、效率降低、过热共6 种症状,可由电流和振动传感器监测获得。将搜集到的样本记录分为两类,即400 组训练样本与400组测试样本,为降低量值差异可能对测量值造成影响,避免出现计算饱和现象,需归一化处理样本数据,使输入样本数据在[0,1]之间,归一化公式为:

其中,x∈[xmin,xmax],xmin和xmax分别为最小值和最大值。
(2)改进算法性能分析。设粒子群规模为25,解空间为400 维,最大迭代次数为1 000,加速度常数φ1=φ2=1.98,初始w=0.92。建立4 个LS-SVM 分类器,γ选取1 000,径向基核函数宽度参数σ2选取为0.125。利用标准粒子群与改进粒子群算法对LS-SVM 中的式(9)进行求解,得到的平均误差曲线如图2 所示。标准粒子群算法在第100 次迭代后达误差精度达到0.26,而改进粒子群算法在迭代相同步数后,精度可达到0.01,在200 次迭代后误差精度达0.001。可见改进粒子群算法比标准算法收敛速度更快,精度更高。
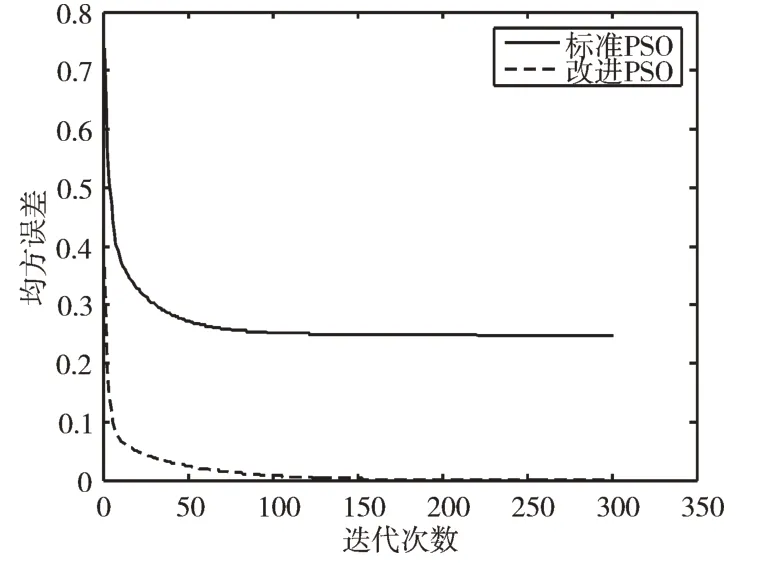
Fig.2 Error curves of standard particle swarm optimization and improved particle swarm optimization图2 标准粒子群算法和改进粒子群算法误差曲线
(3)结果比较。分别用改进粒子群算法迭代后的识别算法和标准粒子群识别算法对400 个故障样本进行识别,并对两者训练时间、测试时间和识别准确率结果进行比较。性能测试结果如表1 所示,训练和测试的变化过程分别如图3—图5 所示。

Table 1 Performance comparison of the algorithms表1 算法性能比较

Fig.3 Training time comparison curve图3 训练时间对比曲线
从性能测试统计结果可看出,在训练时间、测试时间、准确率方面,改进粒子群的LS-SVM 性能优于标准粒子群的LS-SVM,体现了改进粒子群优化算法快速的收敛性能与高精度的分类能力。随着样本数目的增加,两种分类算法耗时均有所增加,但是改进粒子群的LS-SVM 时耗明显低于标准粒子群的LS-SVM,说明改进算法具有优良的适应性能和学习能力,适用于实时场合。
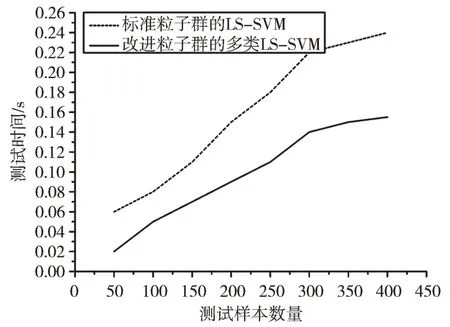
Fig.4 Testing time comparison curve图4 测试时间对比曲线

Fig.5 Accuracy comparison curve图5 准确率对比曲线
3 结语
影响电机故障诊断结果的因素很多,传统诊断方法存在各种不确定性,本文提出基于改进粒子群优化的多类LS-SVM 算法,以迭代计算的方法代替大规模矩阵求逆运算,获得了稳定的快速收敛性能与更高精度。实例证明其效果显著,有较好应用前景。
