基于LSTM-XGBoost 二维组合模型的GDP 增速预测

朱 青，周石鹏

（上海理工大学管理学院，上海 200093）

0 引言

改革开放以来，中国是同期世界上经济发展最快的国家，经济实现了持续高速增长，成为世界第二大经济体。随着科学技术的发展，探索使用大数据和机器学习的方法改进宏观经济结构和趋势成为研究热点，包括对国民经济GDP（Gross Domestic Product，GDP）预测问题的研究。本文通过对经济因素的综合考量，选用GDP 增速作为经济发展趋势的重要评价指标。

GDP 增速反映经济发展趋势，与人民生活水平息息相关。根据中国国家统计局数据，中国经济经过多年的高速增长后，2015 年GDP 增速为6.9%，2016-2018 年增速分别为6.7%、6.8%和6.6%。2019 年GDP 增速为6.1%，是近年来最大的一次经济增速下降。因此，精准预测GDP 增速对宏观经济目标的可行性和有效性分析具有重要影响。

1 相关研究

国内外对宏观变量的预测方法包括两大类：利用模型预测和主观判断性预测。模型预测主要是时间序列方法和机器学习方法［1-3］。李娜等［4］利用ARIMA 模型对国民经济GDP 进行预测研究，表明了ARIMA 模型在GDP 预测方面的优良性；Wang&Shang［5］、Wang 等［6］将改进SVM 模型应用于股票预测，表明改进SVM 模型在预测方面的有效性。对经济进行主观预测的如美国联邦储备委员会，在确定货币政策之前，研究人员对美国经济走势提供主观预测，被称为绿皮书预测。

随着计算机技术的发展，机器学习算法和组合模型越来越多地应用于预测分析。王晓飞等［7］将时间序列模型和神经网络模型进行组合以预测PM2.5。传统时间序列方法，其缺点是要求时序数据稳定，并对复杂的非线性系统拟合能力较差，且容易发生多重共线性，预测精度不够准确。目前，GDP 增速预测模型主要是单一的时间序列模型，本文从两个方面对GDP 增速预测模型进行改进。一是基础模型选取，运用机器学习模型进行GDP 增速预测。机器学习算法包括随机森林（Random Forest，RF）［8］、支持向量机（Support Vector Machine，SVM）［9-10］、神经网络和集成算法［11-13］等。机器学习模型能够模拟非线性可分数据，计算效率和准确率更高。机器学习问题求解流程如图1 所示，模型训练过程如图2 所示。选取机器学习3 个经典模型作为基础模型进行建模研究：①回归模型：Ridge 回归；②集成算法：XGBoost 模型；③神经网路：LSTM 网络。二是增加预测模型维度，提高预测精度。本文使用二维组合模型对GDP 增速进行预测，通过误差倒数法计算权重，对独立模型进行加权组合，对误差较小的模型赋予较大权重，从而可以得到误差更小的预测值。实验结果表明，本文提出的LSTM-XGBoost 二维组合模型的预测精度均高于单一模型预测精度。

Fig.1 Process of machine learning problem solving图1 机器学习问题求解流程

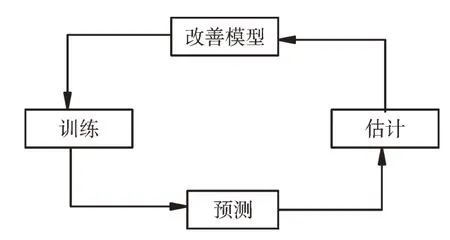
Fig.2 Model training process图2 模型训练过程

2 岭回归预测模型构建

岭回归（Ridge Regression）是Hoerl 等［14］提出的一种改进的最小二乘估计方法。从数学形式上看，岭回归是在最小二乘估计的基础上，向离差平方和增加一个L2 范数。

多元线性回归模型可表示为：

其中，y 为因变量，X为自变量（或者为多变量矩阵形式），β为回归系数，ε为误差。

参数β的最小二乘估计是：

当X不是列满置，XT X的行列式又接近于0，即XT X接近于奇异，此时在计算(XT X)-1时会出错。岭回归就是在矩阵XT X上加一个I，从而使得矩阵非奇异，进而能对I求逆。此时，回归系数β的计算公式将变成：

其中，λ是用户定义的数值。λ越大，消除共线性影响效果越好，但拟合精度越低；λ越小，拟合精度越高，消除共线性影响越差［15］。

3 XGBoost 回归预测模型构建

XGBoost（eXtreme Gradient Boosting）算法是基于回归树的提升算法［16］，其基础树结构为分类回归树［17］（Classification and Regression Tree，CART）。XGBoost 算法已在众多预测领域取得了较好效果［18-21］，其模型参数值如表1 所示。

以下给出回归树数学定义和XGBoost 模型数学推导，如无特别声明，均引自参考文献［16］。

对于给定的n个样本，m个特征的数据集D={(xi,yi)}，其中|D|=n，xi∈ℝm，yi∈ℝ。树集成模型通过k个加性函数预测输出。

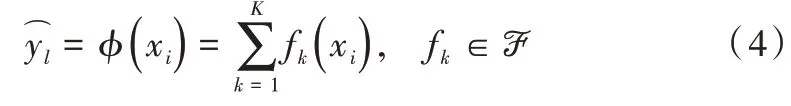
ℱ={f(x)=wq(x)} 是 回 归 树 空 间，其 中q:ℝm→T∣,w∈ℝT是将数据映射到叶子结点的函数，T为树叶子节点的标签集，fk(xi)是第k棵CART 树的预测输出。

损失函数ℒ 如式（5）所示。

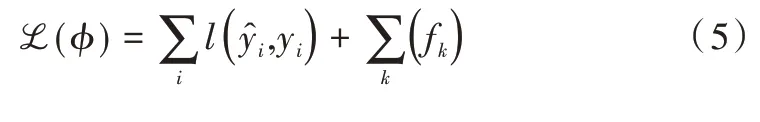
其中：

第t次迭代的损失函数如式（7）所示。

接下来，找到一个ft能最小化目标函数。XGBoost 的思想是将上述目标函数进行二阶泰勒展开，移除高阶无穷小项，得出的目标函数为：

其中，gi、hi分别为损失函数在t-1 次迭代的预测值处的一次和二次偏导。

由于在第t轮时，t-1 轮的结果已知，在第t次迭代中得到更精简的目标函数。

定义好分裂候选集合Ij={i∣q(xi)=j}，进一步改进目标函数。

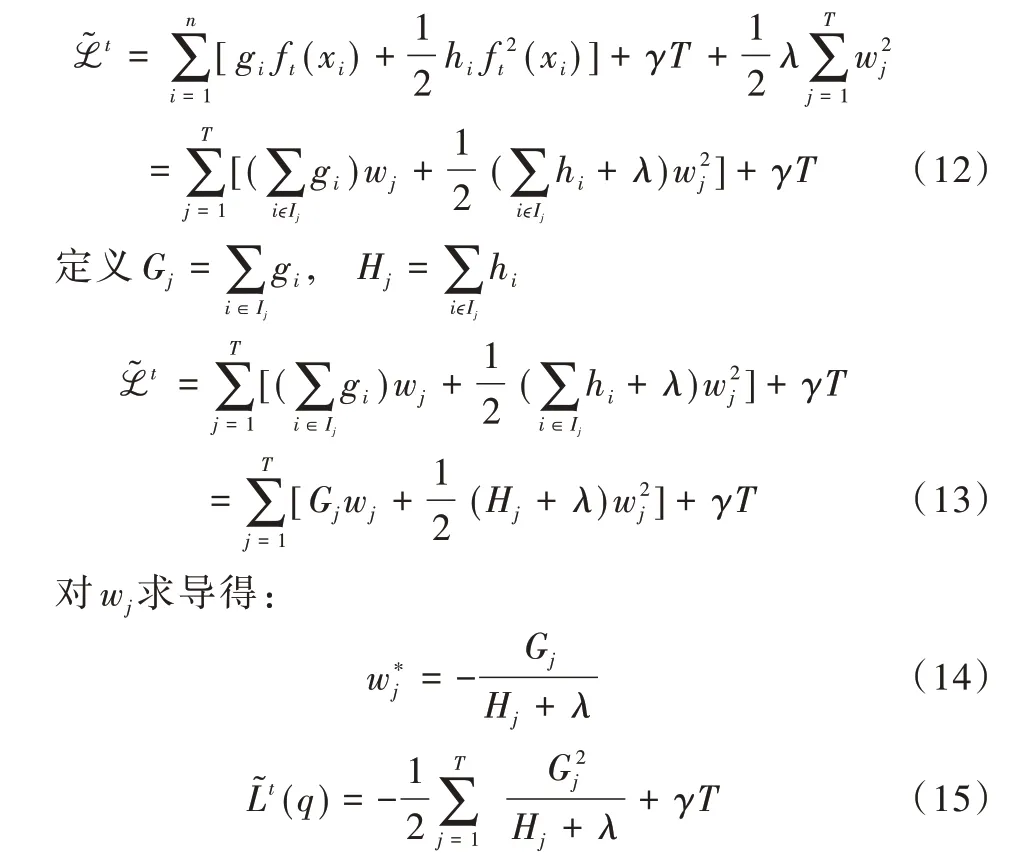
Table 1 Parameter values of XGBoost model表1 XGBoost 模型参数值

4 LSTM 网络预测模型构建

4.1 神经网络

神经网络一般由输入层、隐藏层和输出层组成。图3表示一个3 层神经网络模型。从左至右，第一层为输入层，输入向量为[x1,x2,x3]；第二层为带有4 个节点的隐藏层；第三层为输出层，输出向量为[y1,y2]。

4.2 LSTM 网络预测模型

LSTM（Long Short Term Memory，LSTM）是RNN 的一种改进网络。如图4 所示，LSTM 的单元结构由4 部分组成，分别是输入门（input gate）、输出门（output gate）、记忆单元（memory cell）和遗忘门（forget gate）。LSTM 网络模型参数值如表2 所示。

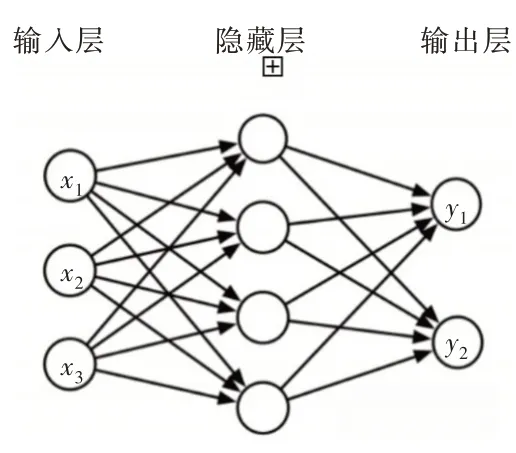
Fig.3 Neural network model图3 神经网络模型

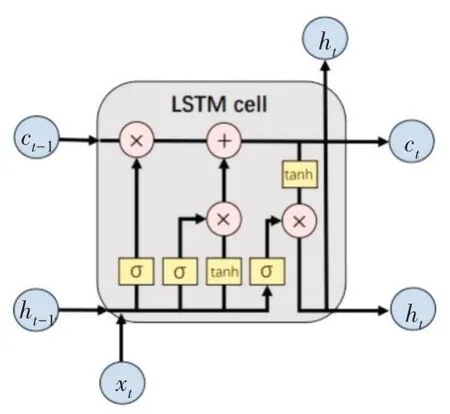
Fig.4 LSTM unit structure图4 LSTM 单元结构

Table 2 Parameter values of LSTM network model表2 LSTM 网络模型参数值

LSTM 各过程具体运算如下：

其中，式（16）中ft为遗忘门输出，表示保留多少信息（1代表完全保留，0 代表完全舍弃），σ表示sigmoid 函数，Wf是遗忘门的权重矩阵，[ht-1,xt]表示将两个向量拼接成一个更长的向量，bf是遗忘门的偏置项。式（17）中，Wi是输入门的权重矩阵，bi是输入门的偏置项。式（18）和（19）中，Wc记忆单元权重矩阵，bc是记忆单元偏置项。表示当前输入的单元状态，Ct表示当前时刻的单元状态，Ct-1表示上一次的单元状态。式（20）中，Wo为输出门权重矩阵，bo为输出门偏置项，Ot为输出门输出。式（21）中，ht为输出门输出结果。

Adam 算法［22］如下：

Require：步长ϵ；

Require：矩估计的指数衰减速率，ρ1和ρ2在区间[0,1)内；

Require：用于数值稳定的小常数δ；

Require：初始参数θ；

初始化一阶和二阶矩变量s=0,r=0；

初始化时间步长t=0；

while 没有达到停止准则do

5 二维组合预测模型构建

通过误差倒数法对模型进行加权组合，计算公式为：

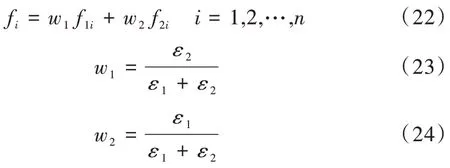
其中，wk是权值参数，fi是组合模型对样本i的预测结果，fki是第k个模型的预测值。ε1是模型1 的预测误差，ε2是模型2 的预测误差。从式（22）—式（24）可以看出，对误差大的模型会赋予较小的权重系数，从而使组合模型误差更小，达到提升预测精度的效果［23］。

6 实验结果与分析

6.1 实验数据

数据来源：国家统计局、快易理财网。本文采用1980-2018 年时间段6 个宏观变量共39 条数据。1 个因变量：GDP 增速（%）。5 个自变量：外汇储备（亿美元）、人口增长率（%）、M2/GDP（%）、财政收入（亿元）和货物进出口总额（亿元）。

数据特点：

（1）数据间具有时序关系。利用过去的信息预测未来经济情况。

（2）数据样本较少。从改革开放以来，国家有完整明确的经济数据年份并不多。

（3）数据样本值变化大。中国的经济发展具有阶段性特征，20 世纪八九十年代经济快速发展，但生产技术不高；改革开放阶段，中国经济高速发展；经过30 多年的增长期后，中国经济进入平稳发展阶段。

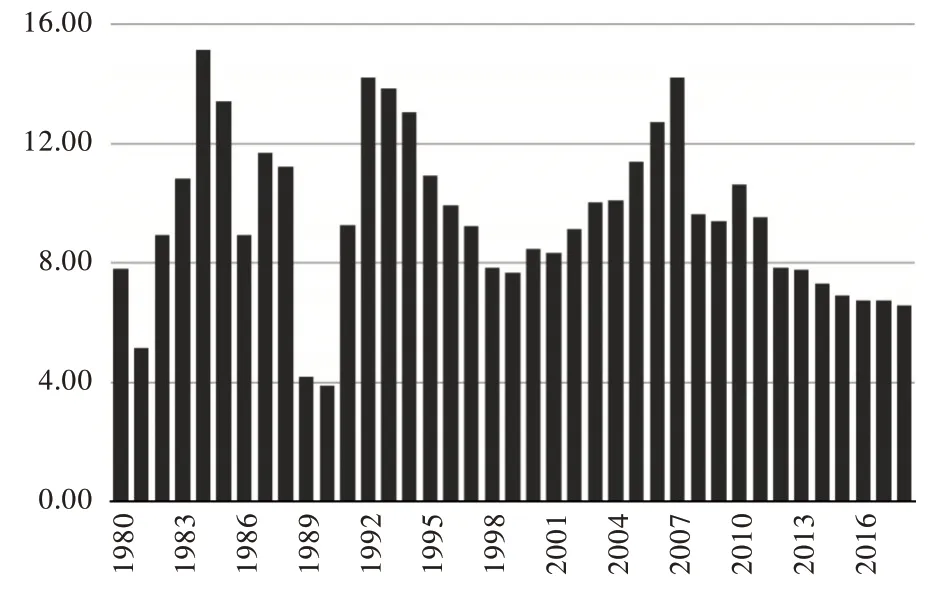
Fig.5 Distribution of GDP growth图5 GDP 增速分布

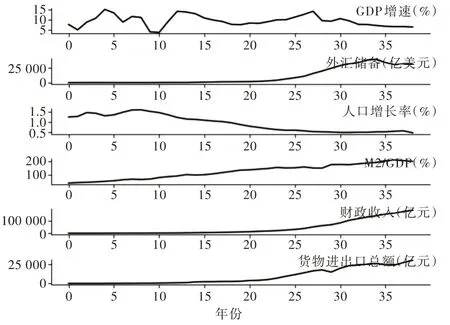
Fig.6 Data distribution图6 数据分布

数据标准化：

其中，μ表示均值，σ表示标准差。本文对数据进行标准化处理，经过处理的数据符合标准正态分布，即均值为0，方差为1 的正态分布。本文先对数据进行标准化处理，再将标准化后的数据用于模型训练和预测，需将预测结果进行反标准化后，才能与实际数据作比较。

6.2 实验环境

本实验所使用开发语言为Python 语言3.7 版本。实验中使用Python 提供的科学计算库，主要包括Numpy、Pandas、Matplotlib、Sklean 等。本文所使用的开发环境为PyCharm。

6.3 实验评价指标

为了验证机器学习回归模型对预测GDP 增速的准确性，本文对数据集中的GDP 增速进行预测实验，并将预测结果与其他模型得出的结果进行比较，比如AR（Auto Regressive Model，AR）、MA（Moving Average Model，MA）、ARIMA（Autoregressive Integrated Moving Average Model，ARIMA）模型，如图7-图9 所示。实验选用均方根误差（root mean square error，RMSE）作为各模型预测性能的主要评价指标，平均绝对误差（MAE）和平均绝对误差百分比（Mean Absolute Percentage Error，MAPE）作为辅助评价指标。通过3 个指标体现模型训练精度及泛化性能。

其中，y代表样本真实值ˆ代表样本预测值，m为样本数据数量。

Fig.7 Comparison of prediction results of Ridge，XGBoost and LSTM图7 Ridge、XGBoost 与LSTM 预测结果对比

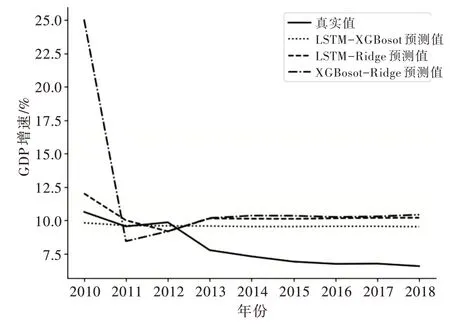
Fig.8 Comparison of prediction results of LSTM-Ridge，LSTM-XGBoost and XGBoost-Ridge图8 LSTM-Ridge、LSTM-XGBoost 与XGBoost-Ridge预测结果对比

从预测结果（见表3—表5）可以看出，3 种算法的3 种评价指标预测结果表现一致，单一模型预测误差的排序是LSTM＜XGBoost＜Ridge，组合模型预测误差的大致排序是LSTM-XGBoost＜LSTM-Ridge＜XGBoost-Ridge。组合模型XGBoost-Ridge 表现较差，整体上，机器学习的单一模型和组合模型的预测效果优于传统时序模型，非线性回归模型整体优于线性回归模型。LSTM-XGBoost 组合模型的拟合效果最好，误差最小，可以达到2.122 的误差，XGBoost-Ridge 回归误差较大，约为5.542。XGBoost 和LSTM 预测结果相近，LSTM 结果略优于XGBoost，LSTM 模型在处理时序问题上有着良好表现，本文数据量偏小，可能无法凸显LSTM 的优势。随着数据集的增加，LSTM 的优势更加明显，预测精度会进一步提高。

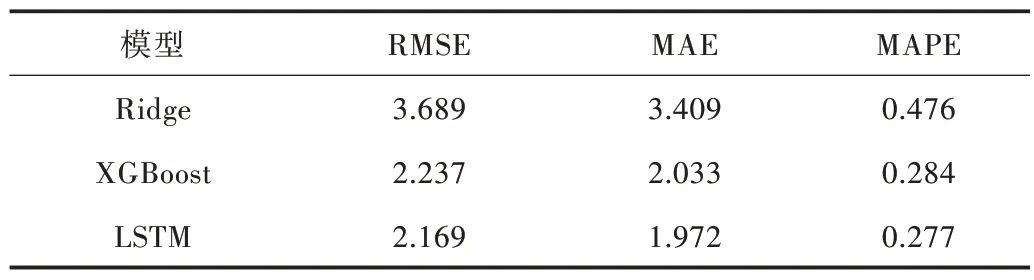
Table 3 Comparison of RMSE，MAE and MAPE in single regression model表3 单一回归模型RMSE、MAE 及MAPE 对比

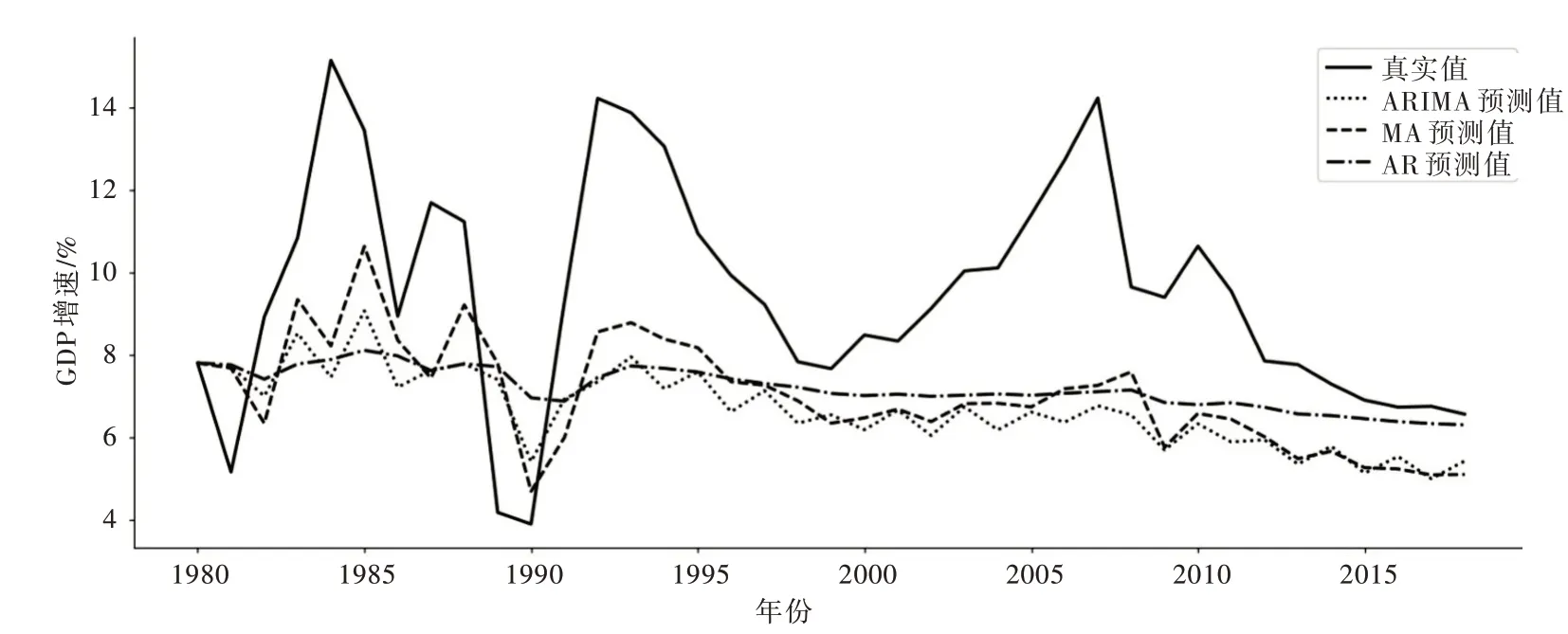
Fig.9 Comparison of prediction results of AR，MA and ARIMA图9 AR、MA 与ARIMA 预测结果对比

Table 4 Comparison of RMSE，MAE and MAPE表4 组合模型RMSE、MAE 及MAPE 对比

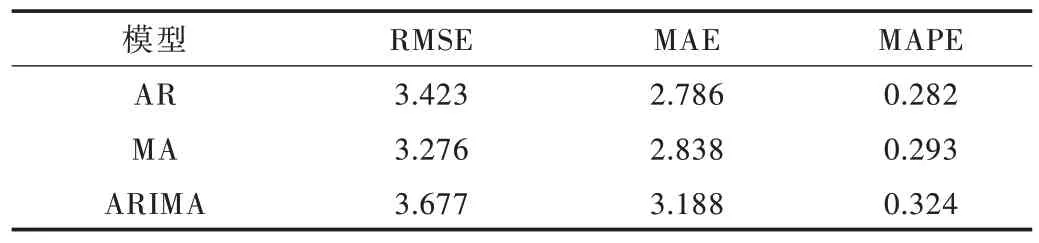
Table 5 Comparison of traditional time series models RMSE，MAE and MAPE表5 传统时序模型RMSE、MAE 及MAPE 对比

7 结语

本文提出LSTM-XGBoost 二维组合模型对GDP 增速进行预测，结果表明该组合模型在宏观经济预测中具有较高应用价值。通过研究机器学习模型在经济领域的应用，得出如下结论：①从XGBoost-Ridge 组合模型中可以得出，并非所有组合模型优于单一模型，模型的正确选择有利于预测精度提升；②本文的误差倒数法存在一定改善空间，误差计算方法是预测值减去真实值，误差值有正有负，使用误差的绝对值或者误差的平方形式计算权重能进一步提高预测精度。后续研究中，可结合大数据等平台，探索机器学习模型应用于经济预测的其他可能性。