超声平面波经颅成像相位校正方法∗

宋亚龙 苏畅,3 李倩岩 林伟军,3

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

(3 北京市海洋深部钻探测量工程技术研究中心 北京 100190)

0 引言

利用超声穿透颅骨对脑组织进行成像，在脑疾病临床诊断和科研上具有重要应用前景。然而当超声穿过颅骨时，由于颅骨的声学特性(如密度、声速、衰减)与周围其他组织差异巨大[1]，导致超声发生严重的衰减和畸变，给超声经颅脑成像带来很大困难。由于超声很难穿透颅骨，目前超声经颅成像一般透过颞骨、枕骨、下颌、眼眶、新生儿囟门等声窗进行，如经颅彩超(Transcranial color-coded duplex sonography,TCCD)和经颅多普勒(Transcranial Doppler,TCD)[2]。而近年来新型匹配材料和声学超材料的发展[3]，可以增强超声穿透颅骨的能量，使超声穿透颅骨其他部位进行治疗或成像成为可能。此时由于颅骨带来的超声相位畸变会使超声图像出现分辨率下降、伪像等问题，需要加以校正以获得准确的颅内图像。

为了补偿和校正颅骨对超声相位的影响，Clement等[4−5]提出利用计算机断层扫描/磁共振成像(CT/MRI)技术构建非均匀颅骨模型，并通过理论建模和数值模拟计算经颅聚焦超声中阵列所需的相位补偿。在应用于脑疾病治疗和神经调控的经颅聚焦超声研究中，Fink[6]、Wu等[7]、Thomas等[8]提出的时间反转法是公认的最常用的解决聚焦偏差的方法。Aubry等[9]提出了结合CT图像的虚拟点源时间反转法，基于CT图像获取颅骨声速模型，利用时域有限差分法对黏性流体介质中的线性声波方程[10]进行数值求解获得超声相控阵各个阵元所接收到的信号，并使用时间反转法计算用于补偿的相位，从而实现超声经过颅骨在颅内精准聚焦。上述研究主要集中于高强度超声聚焦(High intensity focused ultrasound,HIFU)治疗和超声神经调控方面，对于脑部经颅成像的研究相对较少。Ryan等[11]将类似的相位补偿方法应用于经颅被动声成像的接收波束形成，并对比了射线声学理论和时间反转数值模拟两种补偿方法对成像效果的影响。Sukhoruchkin等[12]从超声回波信号中提取颅骨形态信息，用于经颅超声聚焦扫描成像中的相位补偿。Lindsey等[13]基于Snell定律和分层介质模型对三维经颅成像进行了时延校正。Chen等[14]利用射线声学理论与理想合成孔径聚焦技术(Ideal-Synthetic aperture focusing technique,I-SAFT)相结合，补偿经颅成像中的超声相位，校正了图像位置偏差并改善了图像对比度。

另一方面，相比于传统的聚焦扫描成像，平面波成像是一种高速成像方法，具有非常高的成像帧频，有望满足脑功能成像、实时三维成像、实时多普勒血流成像对高帧频的需求。Macé等[15]利用平面波探测鼠的脑部，获得了脑血流动态分布图像。2019年，Du等[16]利用超声发散波发射和深度学习技术进行了经颅成像，通过较小声窗快速对颅脑内的较大区域进行组织结构成像，并进行了相关实验。这些工作中采用的颅骨较薄，因此并没有对颅骨相位畸变进行补偿。胡陈文宝[17]在平面波经颅高精度脑血流成像方面开展了动物实验，并对超声测量颅骨厚度进行了探索。

超声平面波经颅成像中超声的发射方式和传播路径与超声经颅聚焦或被动声成像有较大区别，因此其相位补偿方法也有所不同。本文针对超声平面波经颅成像，利用已知的由CT图像获取的颅骨声速模型，分别采用基于射线声学近似的理论方法以及基于时间反转的全波数值模拟方法，校正平面波经颅入射和反向散射波穿过颅骨时的相位畸变，并利用数值仿真数据对比成像效果。

1 超声平面波成像中的相干复合成像和经颅相位畸变

超声平面波成像时，利用换能器线阵同相位发射超声脉冲，所形成的波阵面近似平面波，波前到达同一深度不同横向位置的时间相同。平面波在声阻抗发生变化的位置发生散射，此时散射点可看作被动点声源，散射波以球面波形式传播并被换能器接收，同一散射点回波到达换能器各阵元的时间与其之间距离成正比。一般的平面波成像假设介质声速均匀，根据成像区域各像素点与换能器阵元的距离关系计算声传播时间，对换能器阵列接收信号进行延迟叠加(接收波束形成)，从而形成图像。与传统的聚焦扫描成像方法相比，平面波一次发射即可获得完整的超声图像，大大提高了成像帧频。单次发射的平面波成像分辨率和对比度较低，调整换能器各阵元发射相位，使换能器以不同角度发射平面波，并使用相干复合成像方法[18]，可以提高平面波成像的分辨率和对比度。

单次平面波成像的发射接收示意图如图1所示，换能器线阵沿x轴排列，各阵元以一定延迟发射，产生的平面波与x轴存在夹角α。以α小于π/2为例，并且以处于坐标原点的阵元x1发射脉冲时为时间起始点，则阵元xk接收到散射点(x,y)产生的散射波的时间为

假设发射的平面波次数为M，与x轴的夹角分别为α1、α2、α3···αM，设RF(xk,t,αi)为不同平面波发射角度下接收阵元接收到的散射回波信号，将公式(1)代到RF(xk,t,αi)中，并且所有接收阵元进行叠加，可以得到成像区域内的像素点(x,y)处的像素值为

当α大于π/2时，结果与α小于π/2时情况类似，不再过多阐述。

当颅骨存在时，由于颅骨本身厚度和声速分布不均匀，超声沿不同路径穿过颅骨不同位置时传播时间不同，颅骨与周围介质声速不同也使从不同角度入射并穿过颅骨的声波传播时间出现差异，因此超声相位会发生畸变。入射平面波经过颅骨后波阵面不再为平面，到达同一深度不同横向位置处的波形相位有差别。而散射波经过颅骨后也不再是球面波，同一散射目标回波到达各阵元的时间与其间的直线距离不再为正比关系。

如果不做相位校正，成像结果会偏离实际散射点位置，并且出现伪像和分辨率下降等问题。因此，本文利用CT图像获取颅骨结构和声学参数模型，并采用基于近似射线声学的理论方法和基于时间反转的全波数值模拟方法，分别计算用于校正的相位偏差。

2 基于近似射线声学的相位校正

不同于图1所示的平面波发射接收，图2显示了平面声波波前到达散射点和散射回波被换能器所接收这两个过程中，声波分别经过了一段颅骨，也正是由于该两段颅骨的存在导致成像结果出现偏差。事实上超声在颅骨内外表面会发生折射，由于颅骨声速与周围软组织差异较大，超声传播路径不应是直线。在本文模型中，颅骨声速分布为非均匀的，超声在其中传播路径较复杂，因此在射线理论相位校正中，本文忽略了超声折射造成的声波传播方向变化，简单地用直线代替声传播路径，并计算该路径上由于颅骨声速变化带来的传播时间差异。

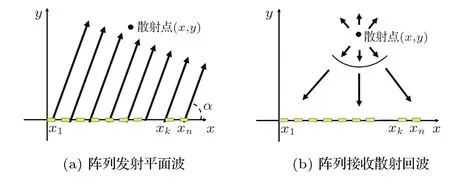
图1 平面波偏转角度发射接收示意图Fig.1 Schematic diagram of transmitting and receiving with plane wave of def lection angle

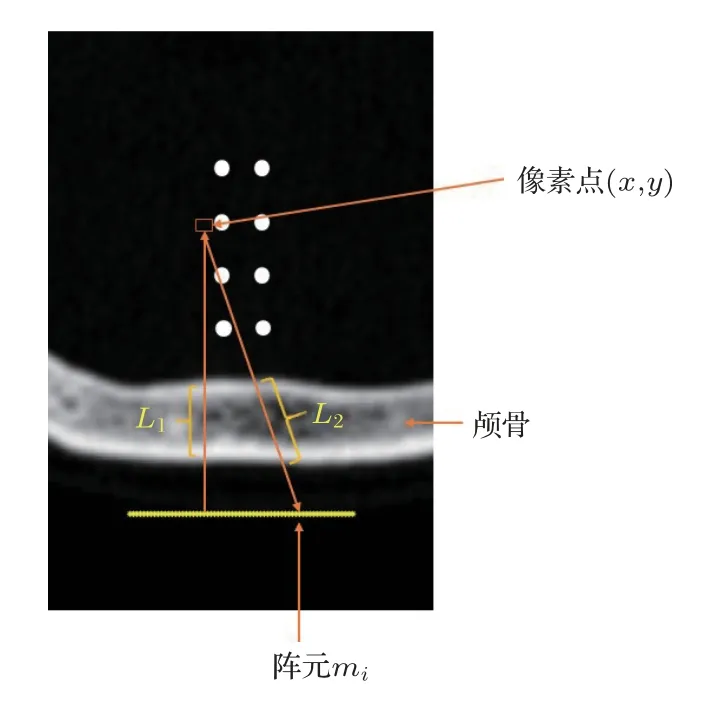
图2 基于近似射线声学理论的声传播路径示意图Fig.2 Schematic diagram of approximated acoustic propagation path based on ray theory

以图2中成像区域内像素点(x,y)为例，平面声波由换能器发射，经过颅骨传播到像素点(x,y)时产生散射回波，再次经过颅骨被换能器阵列中阵元mi所接收到，声波从发射到接收过程中所经过的两次颅骨长度分别记为L1和L2。则两段颅骨造成的时延偏差分别为

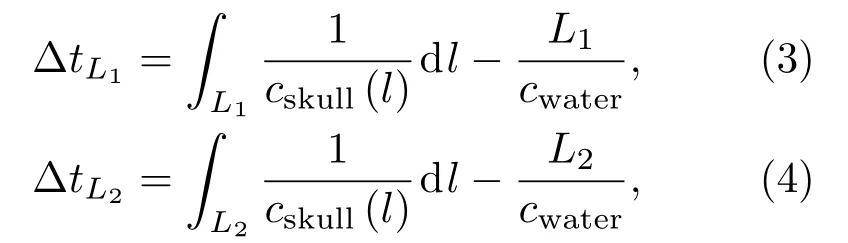
其中，cskull(l)代表的是颅骨的声速，随着颅骨中不同的位置而变化，cwater代表的是使用水的声速代替成像时所使用的颅内脑实质的平均声速(两者数值接近)。可以得到纠正后的像素点(x,y)在阵元mi上的时延为

其中，H1和H2分别代表声波从换能器阵列发射到像素点(x,y)的传播路径长度和散射回波从像素点(x,y)传播到阵元mi的传播路径长度。将公式(5)带入到公式(2)中就可得到经过相位补偿后的像素点(x,y)处的像素值。使用近似射线法进行相位补偿比较直观，易于操作，但本文没有考虑实际声传播路径上的折射效应，会导致一定误差。

3 基于时间反转和数值计算的相位校正和成像

虚拟点源时间反转法在进行超声经颅聚焦过程中有着重要的作用，利用时间反转计算颅骨导致的相位偏差，并在超声发射时加以补偿，可以使超声精准地聚焦至颅内目标处。同样地，在平面波经颅脑成像中，也可以利用时间反转方法来计算和补偿颅骨造成的声波信号相位畸变，在超声平面波入射至颅内和散射波经颅骨向外传播两个过程中，采用时间反转方法分别计算所需的相位补偿量，并分别在发射和接收过程中进行补偿处理。

3.1 时间反转平面波发射相位校正

利用基于虚拟线阵的时间反转数值模拟，可以计算平面波经颅传播时由颅骨导致的相位畸变，进而在超声发射时调控各阵元的发射相位，使超声波阵面在进入颅骨后以类似平面波的形式传播。发射相位调控的过程与时间反转超声经颅聚焦类似，区别在于所用虚拟声源不是点声源，而是一组平面线阵。如图3(a)所示，从颅骨内的虚拟线阵发射声波，将颅外实际用于成像的换能器阵作为接收，利用数值仿真计算颅外换能器各阵元所在位置的声波时域信号，记作fn(t)，其中下标n为阵元编号。从这些信号提取相位差，用于发射校正，具体操作为：设置某一阵元接收到的声波时域信号为参考信号，记为rref(t)，将其他阵元接收到的时域信号与参考信号进行互相关处理[19]，并对参考信号进行自相关处理，从而可得到

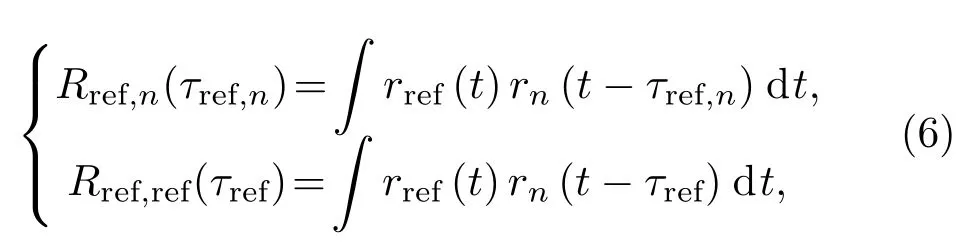
其中，Rref,n表示参考信号rref(t)和第n个阵元接收到的时域声场信号rn(t)之间的互相关函数，Rref,ref是参考信号的自相关函数，τref,n是互相关信号的时间延迟，τref是自相关函数的时间延迟。找出分别使Rref,n(τref,n)和Rref,ref(τref)取最大值的τref,n和τref，就可以求得每个阵元的初始时延补偿。

换能器各阵元利用以上时延补偿调控相位并发射，如图3(b)所示，则声波穿过颅骨时的相位偏差得以补偿，在颅内以近似平面波的形式传播，并且可以准确地获得用以成像的时间延迟。图4给出了各阵元同相位发射时(无发射角度偏转)分别使用近似射线法和全波数值模拟计算得到的由虚拟阵列至实际阵列的各阵元时延偏差，以及它们之间的差值，可以看出，在发射端进行相位补偿时，两种方法之间的相位补偿差值不超过0.2µs。由于换能器孔径相对较小，颅骨表面弧度较小，无角度偏转的平面波可看作近似于垂直入射，因此用直线代替声传播路径的近似射线法在平面波入射段误差较小。

图3 虚拟声源时间反转法用于平面波经颅成像示意图Fig.3 Schematic diagram of plane wave transcranial imaging using time reversal method based on virtual source

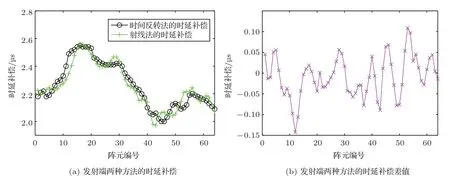
图4 使用近似射线法和时间反转法的时延偏差及其差值Fig.4 Time delay deviation and its difference between ray method and time reversal method

将时间反转法得到的时延偏差用于发射相位校正，利用数值模拟仿真验证效果，图5给出了不加相位校正和时间反转相位校正发射后，颅内距换能器18 mm处接收到的时域声波信号，可见当声波穿过颅骨后，校正后的超声波前可近似看作平面波。

图5 距离换能器18 mm处的声波接收信号Fig.5 Received acoustic signals at 18 mm from transducer

3.2 时间反转接收相位校正

平面波经颅成像接收端的相位校正相对于发射端来讲复杂得多，需要对成像区域内的每个像素点进行相位补偿，这就造成了巨量的计算时间和计算资源，特别是成像区域较大时，不加处理使用传统的时间反转法更是不符合实际需求的。Ryan等[11]将被动声成像焦点处的相位补偿值用于整个成像区域，这是在成像区域集中于焦点附近时采用的近似处理。但平面波声传播路径不同，且成像区域相对较大，必须对不同位置分别计算相位补偿量。为了减小时间反转的数值计算量，本文提出了基于虚拟线阵的理论-数值混合算法。由于颅内的脑实质部分可以近似为均匀介质，超声在颅脑以内的传播过程可以用解析方法计算，而超声穿透颅骨传播的过程则由数值方法求解[20]。为此，在颅脑内靠近颅骨的位置放置一组虚拟线阵，如图6所示。首先，把颅内一个像素点当作被动点声源，点声源发射的声波以球面波形式传播至虚拟线阵，每个虚拟阵元处的声波幅度和相位不同，此过程可解析求解。接下来，虚拟线阵各阵元以此相位延迟和幅度发射发散波，穿过颅骨到达颅外的换能器阵列，可以近似地代替点声源产生的声场，此过程可通过数值模拟结合声场叠加原理来求解。

图6(a)中假设颅脑内侧的虚拟阵列B阵元为Nb个，成像区域内任一像素点S可看作一个被动点声源，该点声源S辐射的球面波到达虚拟阵列B，阵列B各阵元接收到的声波信号为Ais(t−τi)，其中i为阵元序号，Ai和τi可由解析解获得。图6(b)中虚拟阵列B各阵元以Ais(t−τi)为发射信号进行发射，颅骨外的阵列A接收的信号，应与点声源S直接发射时近似相等。实际操作中，阵列B中每个阵元i单独发射，阵列A阵元接收到信号Qj(i,t)，j为阵元序号，根据声场叠加原理，阵列A中阵元j接收的声源S发射的声波信号rcvj(t)可由Qj(i,t)通过延迟加权叠加来获取：

当介质中无颅骨存在时，阵列A各阵元接收的声源S发射的声波信号refj(t)作为参考信号，与rcvj(t)做互相关处理，得到的时间延迟即接收波束形成中的颅骨延时补偿量，可用于成像中的相位补偿。

按传统时间反转方法，对成像区域内每个像素点(x,y)都需要数值计算声传播过程，以获得各阵元的延迟补偿量。而利用以上的虚拟线阵方法，只需进行Nb次声传播的数值计算，大大减少了计算量，同时由于虚拟阵列贴近颅骨，声传播的数值计算区域也可显著减小。

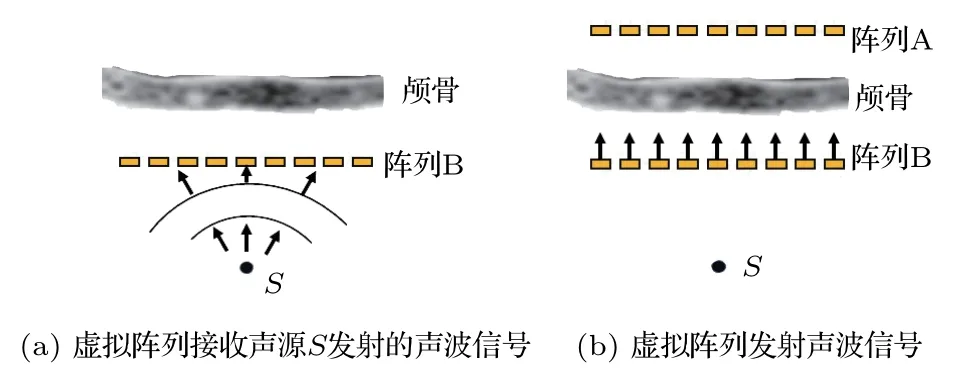
图6 接收相位校正示意图Fig.6 Receiving phase correction diagram

4 数值仿真

根据Aubry等[9]建立的颅骨的声参数与颅骨亨氏值之间的关系可以得到颅骨的声参数：

其中，HU是颅骨亨氏值，可以由颅骨的CT文件中获得；φ是指颅骨的孔隙率；ρmin和ρmax是颅骨中的最小密度和最大密度；cmin和cmax是颅骨中的最小声速和最大声速；本文选取了颅骨中较厚的一段用来构建计算模型，如图7所示。仿真中使用的颅骨和脑实质的具体声参数如表1所示。

表1 仿真使用的声参数Table 1 Acoustic parameters used in the simulation

图7 基于颅骨CT文件的颅骨模型Fig.7 Skull model based on skull CT file

本文根据获得的颅骨非均匀参数模型建立整体的计算模型如图8所示，仿真中所使用的是平面线阵，阵列放置在颅骨外距颅骨大约2 mm处，发射中心频率为2.4 MHz，阵元个数为64个，孔径为25.2 mm，阵元间距约为0.4 mm(略微大于半波长)，阵列发射的声波形式为

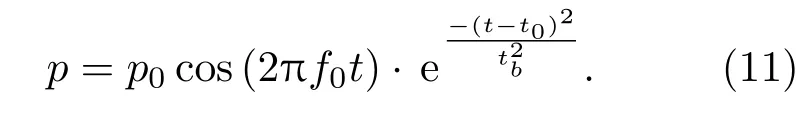
阵列与颅骨之间使用水进行耦合。在颅脑内近似均匀的脑实质环境内放置8个散射目标点，目标点横向间距2 mm，纵向间距5 mm，分布在距换能器20～35 mm范围内，目标点的声速和密度略大于脑实质的声速和密度。

图8 平面波经颅成像计算模型Fig.8 Calculation model of plane wave transcranial imaging

在进行仿真计算时，本文基于流体内的线性声波方程，使用fortran语言编写了空间四阶精度、时间二阶精度的二维交错网格时域有限差分法程序，计算中没有考虑颅骨中的横波，并且忽略了介质衰减。计算区域为x轴方向(横向方向)40 mm、y轴方向(深度方向)60 mm。计算空间步长为0.08 mm，约为水中波长的1/10，时间步长为0.01µs，满足Courant-Friedrich计算稳定性条件。

利用仿真数据，对x轴方向(横向方向)−10～10 mm、y轴方向(深度方向)15～40 mm的区域，用前文所述的平面波成像方法和两种相位补偿方法进行了成像，图9给出了单角度平面波发射时(声传播方向垂直于发射阵列)的成像结果。其中，图9(a)为无颅骨存在时的成像结果，图9(b)为有颅骨但未做相位补偿的图像，图9(c)、图9(d)分别为近似射线法和时间反转法补偿后的图像。图中蓝色点代表散射目标点原本所处位置，图9(d)中的黄色阵列代表时间反转补偿时颅骨内虚拟阵列放置位置(距发射阵列18 mm)。此外，单角度平面波成像往往带来比较明显的伪像，有颅骨存在时进一步增加了伪像，如图9(b)、图9(c)、图9(d)中红色虚线圈出区域所示(部分伪像)。

图9所显示的结果是单角度平面波发射时的成像结果，不可避免地会有平面波成像分辨率差、对比度差等缺陷，实际平面波成像的应用中一般采用多角度平面波发射和相干复合法提高图像质量[18]。如本文第1小节所述，从−10◦～+10◦、间隔1◦发射不同角度平面波，共发射21次。对每个角度发射后接收的超声信号分别使用两种方法进行相位补偿和成像，最后将不同发射角度的结果进行相干复合叠加，得到最终的成像图，如图10和图11所示。图10和图11分别给出了用近似射线法和时间反转法进行相位补偿后，不同相干复合次数下成像的结果。对不同复合次数，平面波发射角度间隔不变，最大偏转角度不同，图10(a)、图11(a)为5次平面波发射相干复合的成像结果，图10(b)、图11(b)为11次相干复合的图像，图10(c)、图11(c)为21次平面波发射相干复合后的图像。

图9 单角度平面波发射时成像结果Fig.9 Imaging results of single angle plane wave emission

图10 近似射线法补偿后不同复合次数的成像结果Fig.10 Imaging results of different complex times after phase compensation with approximated ray method

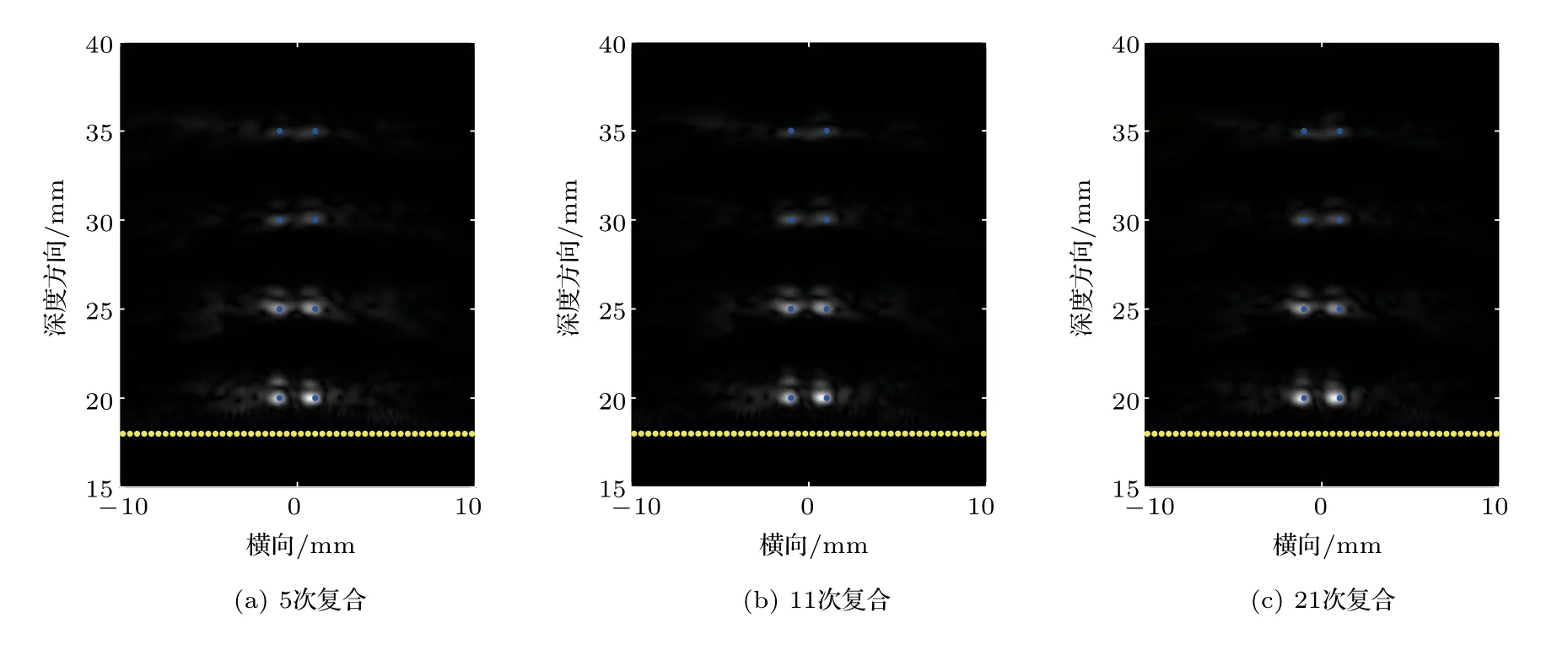
图11 时间反转法补偿后不同复合次数的成像结果Fig.11 Imaging results of different complex times after phase compensation with time reversal method

5 讨论

对比单角度平面波发射时的图像，从图9(a)、图9(b)可以直观地看出，相对于无颅骨存在时，在不进行相位补偿的情况下，颅骨的存在使得图像产生了严重的偏差。首先，像点在深度方向上偏离实际位置，向靠近换能器方向移动，这主要是颅骨声速远大于周围介质声速造成的。其次，图像分辨率下降，在水平方向上相对更为显著，间距为2 mm的两个散射点完全不能分辨，在图中几乎显示为连续界面。此外，图像对比度也有明显下降。

根据图9(c)、图9(d)，使用两种相位补偿方法都能够显著改善成像质量，表2给出了量化的成像质量对比，包括8个目标散射点图像的位置偏差(∆L)、像点水平方向上幅度下降至−3 dB的宽度(W)以及像点最亮处相对于其两侧伪像幅度的对比度(C)。首先，两种相位校正方法都起到了校正像点位置偏差的作用：当没有进行相位补偿时，图像中亮斑与实际散射点的位置偏差平均约为3.8 mm；使用近似射线法进行相位校正之后，像点位置平均偏差为0.4 mm，减小了90%；而在使用时间反转法进行相位校正之后，位置偏差几乎可以忽略不计，所成出的图像可以准确地反映散射目标点所处位置。其次，相位校正对图像横向分辨率有明显改善作用：未进行相位补偿操作时，像点亮斑横向−3 dB的平均宽度约为1.7 mm，远远大于模型中设置的散射目标点的直径0.64 mm，约为水中超声波长的3倍；分别使用近似射线法和时间反转法进行相位补偿处理后−3 dB的平均宽度为1.3 mm和0.9 mm。最后，补偿后的图像对比度也得到显著提高，近似射线法和时间反转法得到的像斑与伪像幅度之比分别提高至未校正时的1.75倍和2.05倍。综上所述，两种相位方法都可以有效地减小颅骨造成的像的位置偏差，提高成像分辨率和对比度。使用时间反转法进行相位校正的精度和效果好于近似射线法，与经颅聚焦超声[9]、经颅被动声成像[11]等研究中结果一致。此外，本文使用的近似射线法时并没有考虑非均匀颅骨造成的声波折射，与严格的射线声学方法[14]相比可能带来了更多误差。

对比图10和图9(c)、图11和图9(d)，不难看出，在经颅成像过程中，平面波相干复合成像可以有效抑制伪像的产生，提高图像分辨率和对比度。此外，同等复合次数下，使用时间反转法相位补偿后的平面波经颅复合成像情况明显好于使用近似射线法相位补偿后的平面波经颅复合成像情况：前者需要复合20次才能获得比较不错的成像结果，而后者复合10次，甚至是5次就可以获得理想的成像效果。

表2 成像结果对比Table 2 Comparison of imaging results

虽然使用时间反转法的相位补偿效果要好于近似射线法的补偿效果，但是其计算过程更为复杂，所需的计算时间远远超过近似射线法。时间反转法需要在成像发射时调整各阵元发射相位，对成像设备及其控制提出了更高要求，在接收相位校正时对虚拟阵列每个阵元做全波声传播过程的数值模拟计算，又需要大量计算资源和时间。以本研究中所用仿真数据为例，对x轴方向(横向方向)−10～10 mm、y轴方向(深度方向)15～40 mm的区域成像，像素点数为400×500。用近似射线法进行相位补偿时，读取颅骨模型和仿真数据、相位校正和成像过程总用时约45 s。而利用时间反转法对相同区域成像时，采用64阵元的虚拟线阵，即需要进行64次二维声场模拟，尽管模拟计算中将虚拟线阵靠近颅骨从而尽量缩小了声场计算区域，并使用了4个进程并行计算以加快速度，一次成像的总用时仍需约3 h，且在计算过程中需要约1 GB的内存来存储所需的双精度参数。以上模拟和成像计算均采用自行编写的fortran软件，在配有4核主频3.10 GHz处理器的PC机上进行。由于时间反转法计算时间过长，暂时还难以在实际的颅脑成像中应用，并且需要高性能计算机和快速模拟算法的支持。此外，两种相位校正方法都依赖于准确的颅骨声速先验模型，而这在实际成像中是难以获取的。因此研究加快颅脑声场模拟计算速度的算法、寻求不依赖颅骨先验模型实时获取颅骨声速的方法或用简化颅骨模型提高颅脑成像精度，是使超声经颅成像走向实用的几个可能的发展方向。

6 结论

颅骨的存在使得在平面波超声经颅成像中的超声传播产生了严重的相位畸变，从而导致成像结果存在位置偏差、分辨率和对比度低等问题。本文分别使用近似射线法和基于虚拟声源的时间反转法对颅骨造成的相位畸变进行了补偿，并利用交错网格时域有限差分求解无黏线性声波方程对穿颅声场进行了建模仿真和成像验证。结果表明：(1)相对于无补偿时的成像结果，无论使用近似射线法还是时间反转法，都能够有效地校正因颅骨造成的相位畸变，从而减小像点位置偏差、分辨率、对比度低等问题。(2)使用时间反转和近似射线法的仿真结果存在微小的偏差，主要是由于在使用射线法时并没有考虑颅骨造成的声波折射，从而在确定声传播路径时存在一定误差。(3)时间反转法成像的精度要好于近似射线法，但所需的计算资源和时间都要远远大于近似射线法。(4)无论近似射线法还是时间反转法，经过平面波多角度发射和相干复合处理后都能够一定程度上提高成像的对比度和分辨率。

致谢感谢浙江大学医学院附属第四医院提供的颅骨CT扫描文件。