基于动力学仿真数据的高速列车蛇行状态识别
2021-04-22方明宽陈春俊
赵 飞,宁 静,2,方明宽,陈春俊
(1.西南交通大学机械工程学院,四川 成都 610031; 2.轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)
0 引 言
从铁道车辆的诞生开始,车辆运行的安全性就一直备受人们关注。车辆运行安全性的主要关注问题就是车辆系统的横向稳定性。自从英国的Stephenson在1821年首先注意到车辆系统的蛇行现象,铁道车辆的横向稳定性就一直被很多学者关注。铁道车辆的蛇行运动是一种自激振动,由于其轮对踏面具有锥度,在运行过程中必然存在蛇行运动[1]。近年来,随着高铁的快速发展,对车辆运行的安全品质有着越来越高的要求。孙丽霞[2]提出基于轮对横移加速度移动均方根、转向架横向振动加速度和脱轨系数的高速列车动态脱轨安全性综合评价方法。宋欣武[3]通过对轴箱横向振动信号与构架横向振动信号的综合分析来评估转向架的运行状态,提出了横向位移峰值方法(LMP),即把轮对和构架的横向振动加速度信号通过计算得出轮对横移量的峰值来判定车辆是否失稳。Zeng等[4]利用车辆发生蛇行运动时车体,构架,轮对的横向振动信号具有周期性的特点,计算其相位轨迹的周期性指数(PIPT),设定阈值来判断车辆是否发生蛇行。
近年来,随着人工智能技术的发展,人工智能学习算法广泛地运用于特征识别。Ye等[5]通过对构架的横向、垂向和纵向加速度信号的融合,提出了一种基于独立模式函数重构与线性局部切空间对齐(IMFR-LLTSA)的特征提取方法,用于识别小幅蛇行,提高高速列车运行的安全性。Sun等[6]通过对高速列车的车体和构架的横向加速度信号进行互相关分析,找出最优的互相关指标并设定阈值,以此来识别不同的车辆运行状态(正常,小幅蛇行失稳,大幅蛇行失稳)。崔万里[7]通过样本熵理论以及等距映射算法(ISOMAP)对信号进行特征提取,然后通过LS-SVM进行特征识别达到较好的识别效果。叶运广[8]通过MEEMD进行特征提取与特征识别亦取得很好的效果。然而,由于高速列车运行数据获取困难,蛇行失稳数据样本少且极度不均衡,因此,人工智能模型验证的数据较少,无法建立复杂度更高的模型。
基于以上分析,针对高速列车实测的蛇行失稳数据样本少且极度不均衡问题,本文通过SIMPACK软件建立高速列车的动力学仿真模型,模拟蛇行失稳获取仿真数据,对仿真数据和实测数据进行差异性分析,再用人工智能模型对仿真数据进行验证。以解决人工智能模型用于高速列车状态识别上的数据不足问题,有利于建立更为复杂的模型。
1 高速列车动力学建模和仿真
1.1 建模方法
车辆的横向运行稳定性是轨道车辆研究的一个重点课题,其中最重要的就是车辆的蛇行运动,车辆系统动力学是多体系统动力学的一个分支,因此,动力学系统的建模方法大多都适合轨道车辆。动力学系统的建模方法包括牛顿-欧拉方程、Lagrange方程、D’Alembert原理、多刚体动力学法、Kane方法、Roberson-Wittenburg方法和变分方法等。本文选取了经典的牛顿-欧拉方程对高速列车进行建模。
牛顿-欧拉方程的主要建模过程:首先,根据研究对象,对所研究的系统动力学系统进行简化,抽象出主要的刚体和连接元件;其次,刚体用来描述动力学系统的惯性特性;再者,连接元件用来描述各个刚体之间的相互作用的刚度和阻尼特性;最后,根据牛顿第二定律得到动力学系统的3个位移方程,再根据欧拉方程得到动力学系统的3个转动方程,其一般形式为:
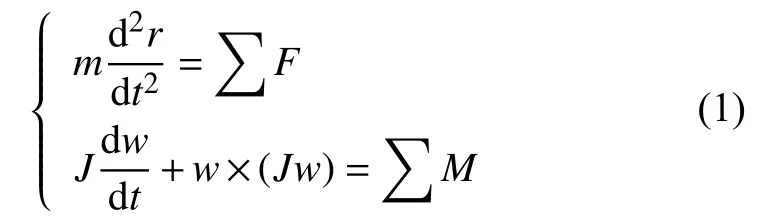
式中:m——质量;
r——位移;
F——所受外力;
J——转动惯量;
w——转动角速度;
M——所受力矩。
根据方程(1)得出每个刚体的位移、转动微分方程和约束方程,组成系统动力学微分代数方程组。
1.2 半车-转向架横向运动模型
一般而言,根据不同的研究目的,需要建立的车辆动力学模型也会有差异。虽然把车辆的每个自由度都考虑进去能使结果更加准确,但会使分析和求解过程繁琐、复杂化。高速列车的蛇行运动是轨道车辆的横向稳定性范畴。因此,本文关注的重点是高速列车的横向稳定性问题。针对本文所考虑的高速列车蛇行运动问题,建立半车-转向架横向运动模型。模型中只考虑了与横向运动相关的自由度即横移和摇头。模型包括一个构架、两个轮对,以及一系和二系悬挂。该模型的基本假设[1,9-11]:
1)车体位于二系悬挂之上,且视为固定状态,只考虑其质量。
2)两个轮对和构架视为刚体。
3)转向架的横向运动和垂向运动是弱耦合的,便于考察其蛇行运动。
4)轮对和钢轨在垂向上始终保持接触,轮对具有轮缘。
5)忽略轮对的自旋效应,轮轨接触关系仅考虑等效锥度。
根据式(1)建立转向架系统横向运动的微分方程如下:

FT(y)——轮缘接触力,如图1所示;

图1 轮缘接触力FT
c2x——抗蛇行减振器阻尼系数,如图2所示。
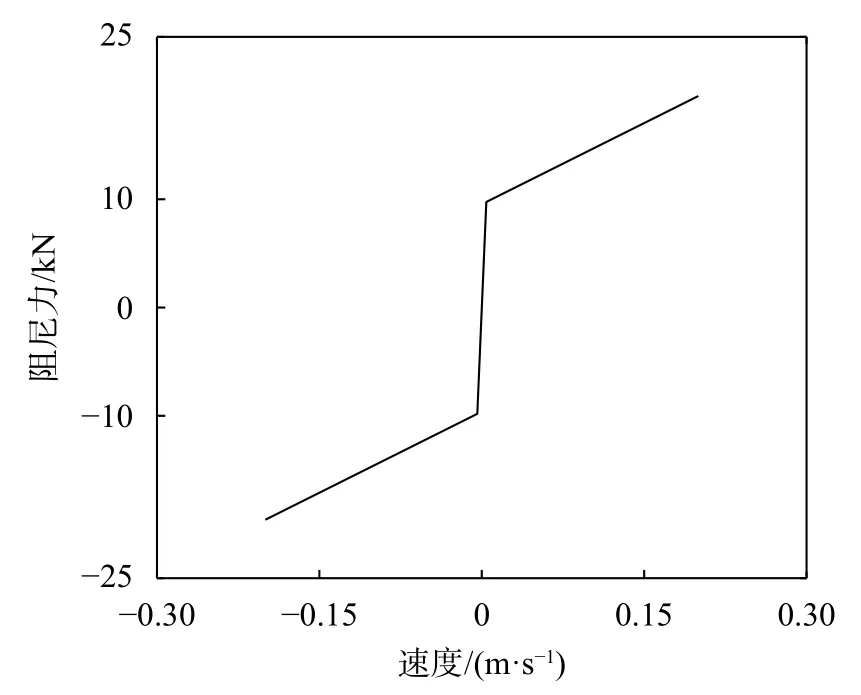
图2 抗蛇行减振器阻尼系数
式(2)中其他参数如表1所示。

表1 半车-转向架系统参数
本文选择翟方法-新型快速数值积分方法[12]对式(2)进行计算,计算出模型的非线性临界速度为410 km/h。
1.3 高速列车仿真模型及数据仿真
本文基于SIMPACK软件建立某高速列车的动力学仿真模型,该高速列车模型的基本参数如表2所示,建立的高速列车模型如图3所示。

图3 某高速列车的动力学仿真模型

表2 动力学模型的基本参数
该动力学系统仿真模型包括4个轮对、8个轴箱、2个构架、1个车体、一系悬挂系统和二系悬挂系统。其中车体、构架和轮对具有6个自由度且视为刚体,轴箱只有1个点头自由度且视为刚体。在一、二系悬挂系统中,一系垂向减振器、抗蛇行减振器、横向减振器和横向止挡具有非线性,轮轨接触几何也具有非线性,因此该高速列车动力学模型是一个非线性系统。通过对该高速列车动力学仿真模型进行仿真计算,得到该高速列车模型的非线性临界速度为406 km/h,与1.2节的半车-转向架动力学模型计算的非线性临界速度基本一致,表明建立的高速列车的动力学仿真模型合理,可以用于后续的仿真计算。
为了容易获取小幅蛇行失稳和大幅蛇行失稳的构架横向加速度数据,调整车辆的抗蛇行减振器阻尼,施加轨道激励,车辆以350 km/h速度运行,测量构架的加速度信号[6]。通过仿真得到构架横向加速度数据,再经过0~10 Hz低通滤波,小幅蛇行失稳数据和大幅蛇行失稳数据如图4所示。图5为国内某高速列车实验实测的构架横向加速度数据,通过对比可以看到仿真数据和实测数据的加速度幅值范围基本一致,仿真数据和实测数据在时域特征上具有相似性。
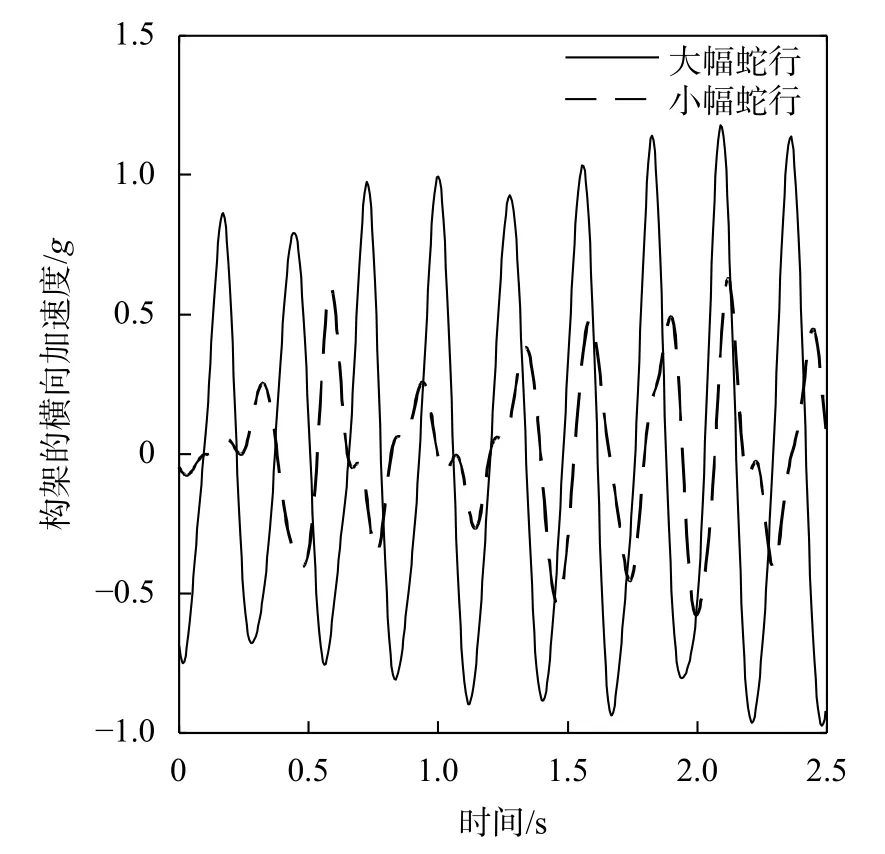
图4 仿真的构架横向加速度时域图
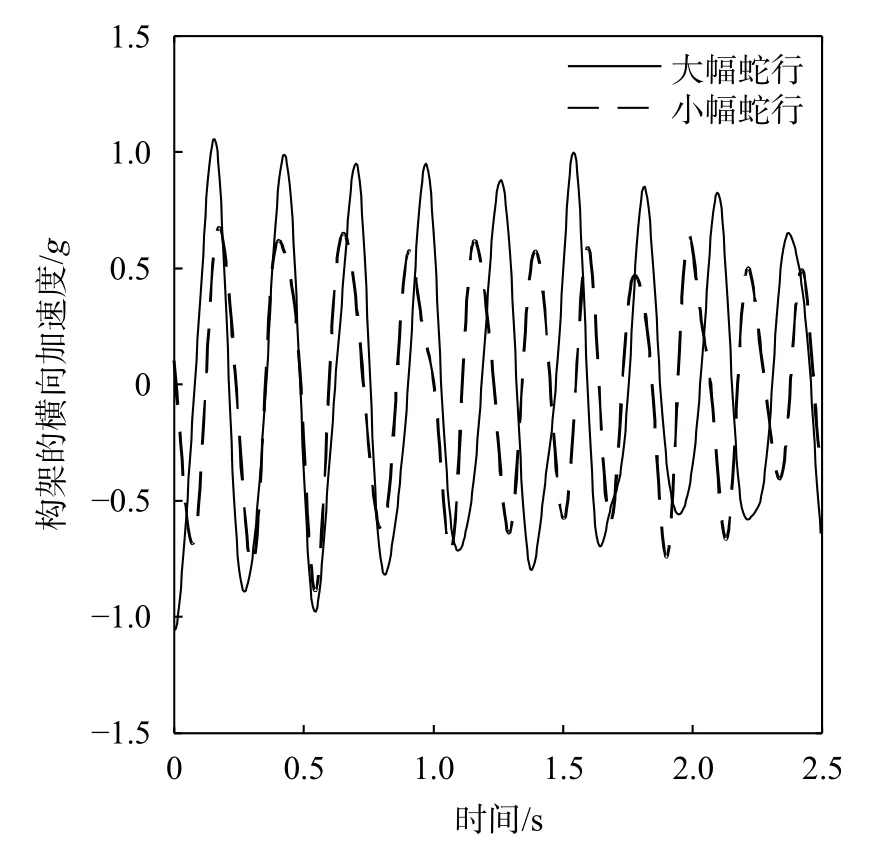
图5 实测的构架横向加速度时域图
2 仿真数据与实测数据的差异性分析
2.1 仿真数据与实测数的互信息分析
互信息是反映两个随机变量之间相互依赖程度的一种量度,也称为转移信息,是度量两个事件集合之间的相关性的一种指标。
将相同长度的仿真数据与实际数据一一对应,并计算互信息量,结果如图6和图7所示。从图上可以看到,其互信息系数主要落入区间0.7~0.8,结果表明实际数据与仿真数据在时域上表现具有高度的类似性。

图6 小幅蛇行数据的互信息分析

图7 大幅蛇行数据的互信息分析
2.2 仿真数据与实测数据的HHT分析
希尔伯特-黄变换(HHT)中,EMD分解是核心算法,EMD分解先将时间特征尺度小的高频IMF(本征模函数)分量分离出来,然后将时间特征尺度大的低频IMF分量分离出来,再根据停止准则,最后得到一个近似单调的残余分量。HHT时频特征谱能准确地分解出各成分的频率,HHT边际谱能直观、准确地找到频率点[13]。
图8~图11为实测和仿真数据的HHT时频特征谱分析,可以看到,仿真数据的主频率与实测数据的主频率所在的范围基本一致,这说明实测数据的时频特征与仿真数据的时频特征具有较高的相似性。图12~图15为实测和仿真数据的HHT边际谱分析,可以看到无论是真实数据还是仿真数据,小幅蛇行数据与大幅蛇行数据的主频率主要落在5 Hz附近,即实际数据与仿真数据具有相似的频率特征。
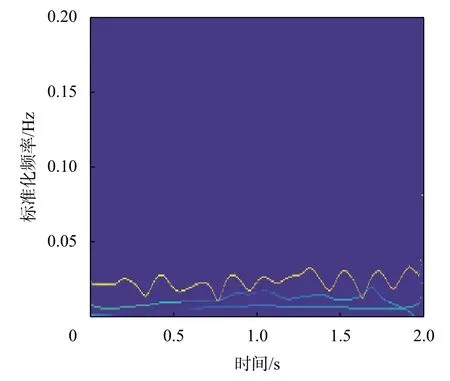
图8 实测小幅蛇行数据的时频特征
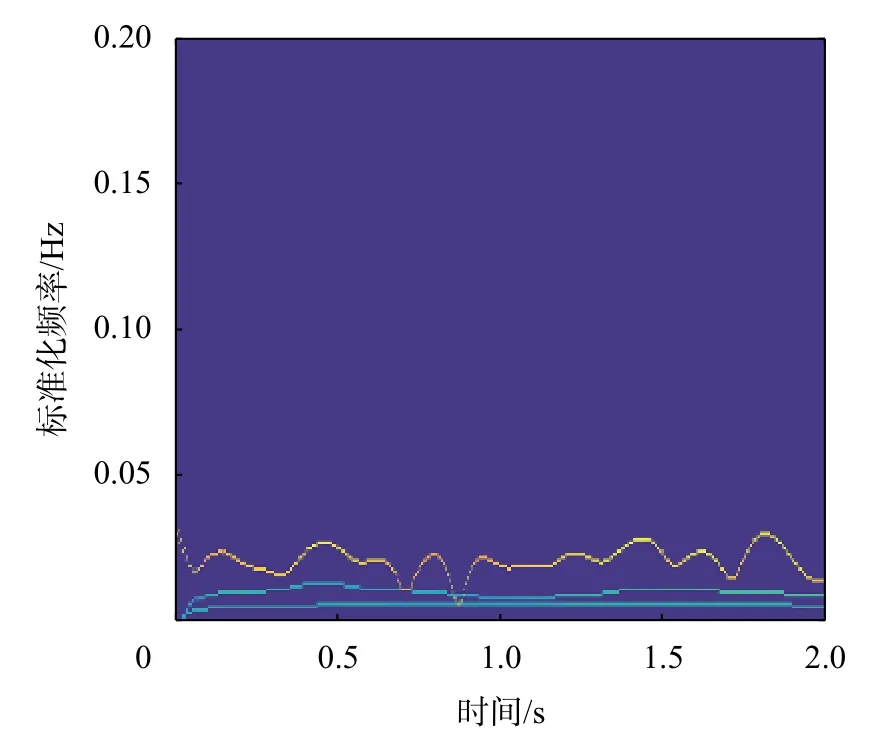
图9 仿真小幅蛇行数据的时频特征
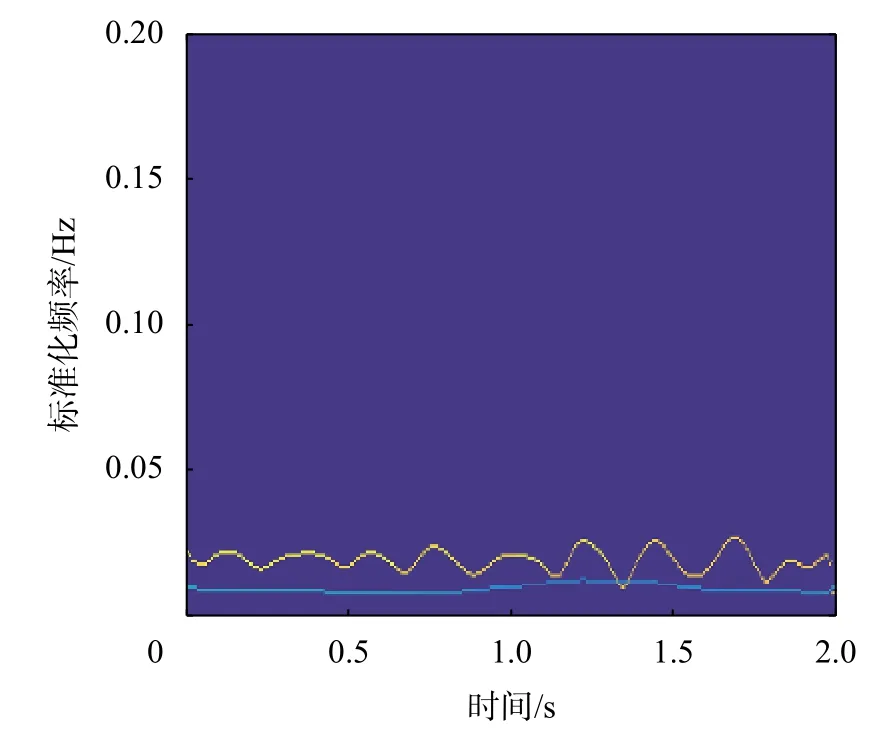
图10 实测大幅蛇行数据的时频特征

图11 仿真大幅蛇行数据的时频特征

图12 实测小幅蛇行数据的边际谱
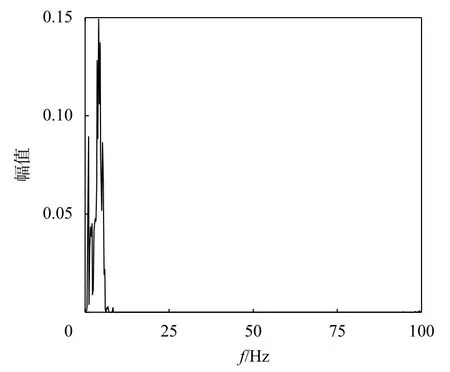
图13 仿真小幅蛇行数据的边际谱

图14 实测大幅蛇行数据的边际谱

图15 仿真大幅蛇行数据的边际谱
综上分析,可以得出仿真的蛇行失稳数据与实测的蛇行失稳数据在时域与频域上具有较高的相关性,仿真的蛇行失稳数据能够较好反映实际信号的时频特性。
3 仿真数据验证
在从信号分析的角度分析了仿真数据与实测数据的相关性后,为了进一步验证仿真数据能够应用于机器学习模型的训练,使用一些较为常用的机器学习模型(EEMD-SVD-LTSA[14]等)和已经用于高速列车运行状态识别的深度学习模型(CNN-LSTM[15]、EEMD-CNN-LSTM等)来对仿真数据进行验证。其具体方法是将仿真数据作为训练集来训练模型,将实测数据作为测试集来验证模型对高速列车蛇行失稳的识别和分类能力。数据的具体描述如表3所示。

表3 数据说明
表4为常见的机器学习和深度学习方法的分类结果。结果表明,无论是机器学习模型还是深度学习模型,均能通过仿真数据进行训练,再来识别和分类真实数据中的蛇行失稳状态,并得到了较好的结果。这说明了基于高速列车的仿真模型获得的数据能够用于深度学习模型的训练,从而解决实测数据中蛇行失稳样本少,且难以采集的问题,从而能够通过有限的实际数据建立更为复杂的深度学习模型。

表4 分类算法的结果
4 结束语
为了能够解决实测数据中的蛇行失稳数据样本少且不均衡的问题,本文通过建立高速列车的动力学仿真模型,模拟出高速列车的各种运行状态数据。通过对仿真数据和实测数据进行差异性分析和对仿真数据进行验证,可以得出以下结论:
1)仿真数据在时域和频域上都和实测数据相似。
2)仿真数据可以作为训练集用于复杂的深度学习模型。
本文只分析了构架的横向加速度数据,没有分析车体和轴箱的加速度数据,希望能在后续工作中对其做更深入的研究。
