H-Bot 型3D 打印机动力学参数辨识与定位误差补偿
2021-04-22曹深深毕德学邹绍昕
曹深深,毕德学,邹绍昕
(1. 天津科技大学机械工程学院,天津 300222;2. 中国人民解放军32182 部队,北京 100042)
3D 打印是一种快速成型的技术,是区别于传统减材制造的一种加工方法[1].它的出现使得制造模式由大批量的固化生产转向小规模的个性化生产,满足了人们在家即可完成发明、创新和低成本的个性化生产等一系列过程的需求[2].从桌面级3D 打印机用户使用层面的角度分析,高打印精度的3D 打印机造价较高,很难真正普及使用;成本较低的3D 打印机打印精度又无法满足需求[3].因此,如何在节约成本的基础上有效提高定位精度的问题成为约束3D 打印机普及的重要障碍.目前国内外也提出一些提高打印机精度的方法.罗德岛大学的Sollmann[4]通过建立动力学模型,用误差参数进行补偿的方法提高了同步带定位机构的精度;河北工业大学的丁承君等[5]引入了布兰森汉姆(Bresenham)直线算法实现了对H-Bot机构运动误差修正;燕山大学的李江滨[6]通过建立3D 打印机的误差参数模型,采用误差参数辨识和补偿的方法提高了末端执行器的位置精度.
本文提出对3D 打印机的单轴进行标定,该方法在小型通用自组打印机的硬件条件下,可以将打印机定位误差降低到原来的1/10.
1 运动模型分析与简化
为了研究提高H-Bot 型3D 打印机的定位精度的方法,需了解打印机的传动结构,并找出影响运动误差的因素.在H-Bot 型3D 打印机系统中,xy 方向的执行器为同步带牵引的H-Bot 结构,可视为由多段弹性体串联而成,其原模型如图1(a)所示.打印机运动一般受电机的输出转矩、运动机构的惯性以及系统内部的非线性摩擦等因素的影响.假定滑块质量mcart,滑桥质量mbridge,滑轮质量mp,转动惯量 Jp,同步带的质量可忽略不计.摩擦力主要是直线轴承与光轴的滑动摩擦,且其模型为非线性模型,除黏性摩擦还有库仑摩擦.摩擦力的模型为

式中:f 表示黏性摩擦因数;v 表示运动速度;cF 表示库仑摩擦力.
假设滑块与滑桥之间的黏性摩擦因数为 bcart、库仑摩擦力为 Fccart,滑桥与固定滑轨之间的黏性摩擦因数为 bbridge、库仑摩擦力为 Fcbridge.
打印机在执行复杂轮廓时,电机需要在短距离高速运动条件下频繁启停、换向,采用指数型加减速控制.假设步进电机阻力矩为 Tt=Ktω,加速转矩为J,负载运动方程为

式中:0T 是电磁转矩;J 是负载转动惯量;Kt是转矩常数;ω是电机角速度.
拉格朗日方程对于解决复杂的非自由质点系的动力学问题十分方便[7-8],拉格朗日方程为
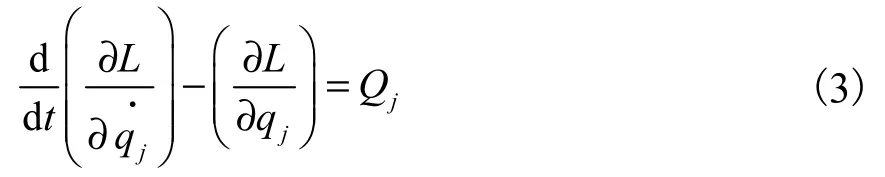
式中:L 是拉格朗日函数.
如图1(a)所示,滑轮在一定程度上被认为是可自由转动的,将1φ—8φ和x、y 分别被定义为角量广义坐标和线量广义坐标,即10 个自由度.广义力的表达式为
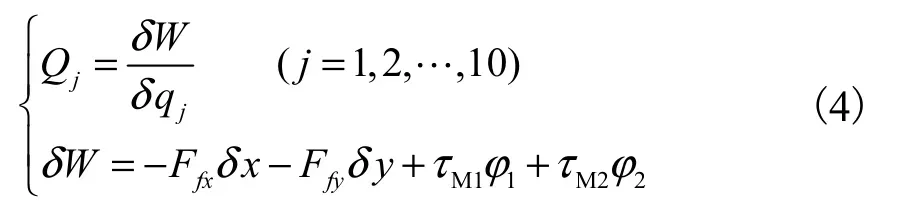
式中: Wδ为系统中非保守力的虚功;δqj为沿广义坐标方向的虚位移;Qj为每个自由度的广义力.
对于微控制器来说,传统的10 自由度传动计算量较大,需尽量简化模型,减少控制器运算时间.通过对模型中的变量进行复合,将除了滑桥上的滑轮之外的所有滑轮的惯性复合到电机滑轮上,此时JMi=2Jp( i=1,2). 只有当滑块沿x 方向有位移时,才考虑滑轮的惯性,并将其复合到滑块的质量中去[9].此时新的滑块质量为

式中:mcart20是未简化的原模型中滑块的质量;mcart8是简化后的简化模型中滑块的质量.
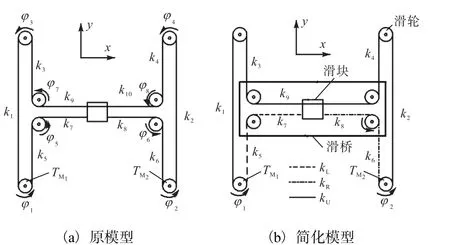
图1 H-Bot 系统广义坐标示意图Fig. 1 Generalized coordinate diagram of H-Bot system
简化后,除电机滑轮外,其余滑轮均视为理想滑轮,系统中的广义坐标减少为4 个,即线量广义坐标x、y 以及角量广义坐标1φ、2φ.对广义坐标简化后,同步带的弹性系数也相应进行简化,将同步带划分为3 个部分 kL、kR、kU,每一部分由多段弹性体串联而成,如图1(b)所示.弹性系数表示为
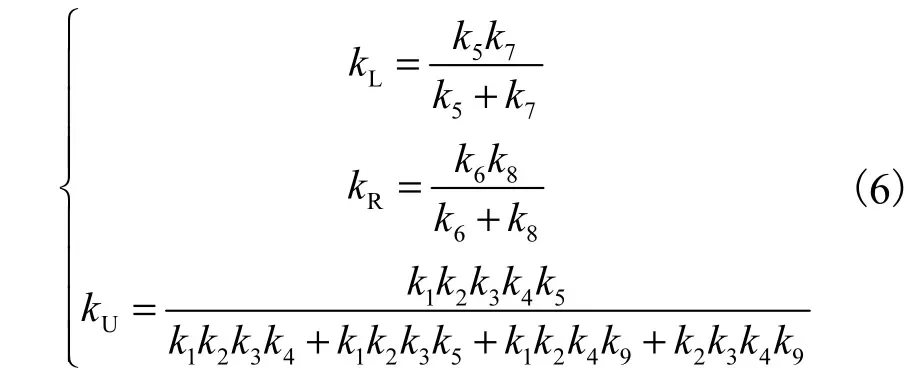
通过以上简化,求得运动方程为

2 动力学仿真模型搭建
机械系统是连续的动态系统,只能通过微分方程来描述[10],对系统的数字仿真需要将描述系统运动的微分方程通过泰勒展开式进行离散化,可借助MATLAB 中的动态系统建模和仿真的集成环境Simulink 来实现.根据简化后H-Bot 结构动力学方程式(6)—(10),建立运动学仿真模型,如图2 所示.模型中的 1x — x8 分别表示
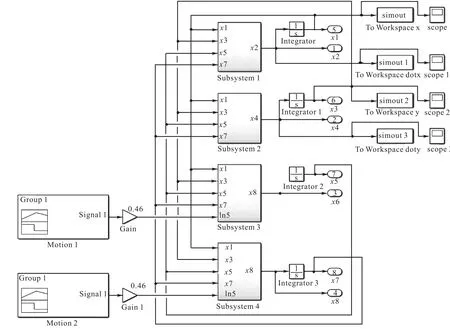
图2 Simulink 仿真模型Fig. 2 Simulink model
3 初始化模型参数估计
在仿真模型中,T0、Kt、JM、mcart、kL、kR、kU、bcart、bbridge、Fccart、Fcbridge等参数无法通过测量等方式精确获取,又对仿真结果产生不同程度的影响,则将这些参数视为一系列的影响因子,通过实验进行参数辨识.通过基恩士激光位移传感器以0.01 s 的间隔采集平台在y 方向分别用0.75 s 和0.25 s 运动8 mm 两组实验,其运动实际距离分别为 7.867 mm 和7.979 mm. 绘制运动曲线图如图3 所示.
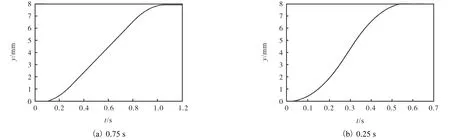
图3 y 方向运动位移曲线图Fig. 3 y direction motion displacement curve
根据图3 的实际运动位移曲线,结合经验确定每个参数基本的数量级,然后通过重复实验对各个参数进行估计,估计值见表1.
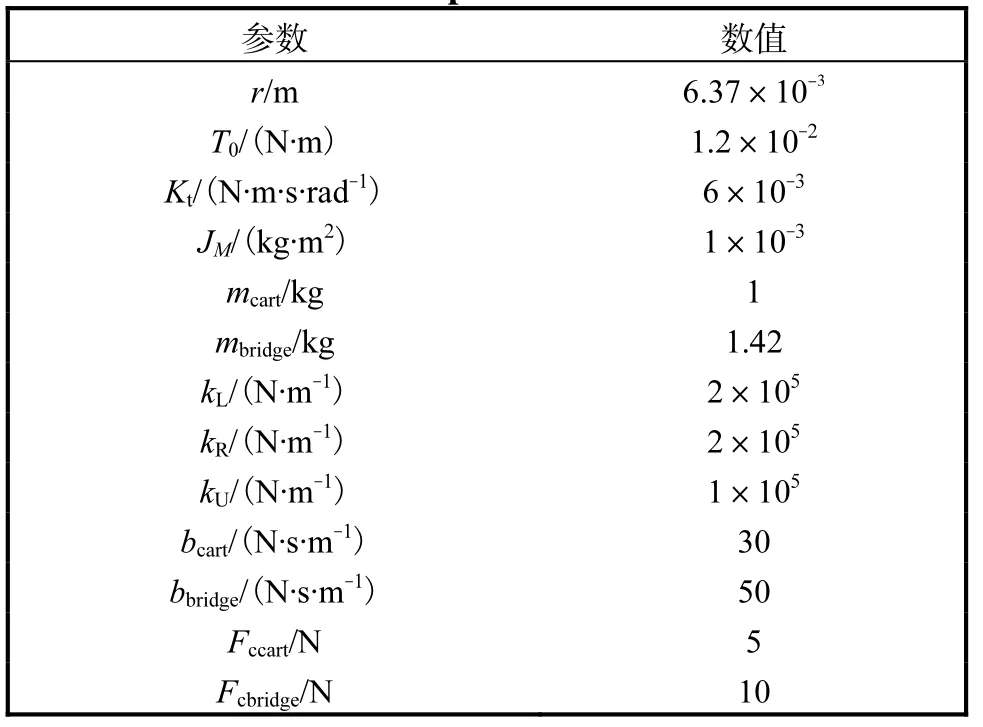
表1 动力学参数估计Tab. 1 Kinetic parameter estimation
按照表1 中参数设置进行仿真运动8 mm 实验,并将仿真曲线与传感器测得的实际运动位移曲线比较,结果如图4 所示.仿真结果与实际情况偏差较大,需对仿真中的参数进行辨识和优化.

图4 y 方向运动位移和仿真位移曲线图Fig. 4 y direction motion displacement and simulated displacement curve
4 参数辨识与优化实验设计
实验的目标是使仿真结果与真实运动距离的差值s 尽可能小作为实验的评价标准.在y 方向的传动机构运动实验中,通过控制变量法对各个参数进行显著性分析,以表1 中的经验估计值为基准,每个参数范围分别取估计基准的0.5 倍和2 倍.实验时,在表1 数据的基础之上,每次控制一个变量变化,所得实验结果见表2.
由实验数据可得:kL、kR、kU3 个参数在其3 个水平下对实验结果的影响不显著,其对实验的影响忽略不计,分别取kL=1×105N/m、kR=1×105N/m、kU=1×105N/m.其余参数均对实验结果有较显著影响,需通过正交实验进一步优化数据组合.

表2 控制变量实验结果Tab. 2 Control variable experiment results
通过 Minitab 软件的田口设计功能获取该五因素三水平的正交实验表,并设置正交实验中各个参数的水平取值范围,每个参数取3 个水平值,见表3,正交实验结果见表4.

表3 正交实验参数水平值Tab. 3 Orthogonal test parameter level
评价标准为测量值与仿真值之间的差值越小,结果越优.观察表 4 中的实验数据,最优组合为a2b2c2d1e1,按照最优组合对应的参数代入仿真模型之中,绘制仿真曲线与实际运动曲线,结果如图5 所示,拟合效果较好.
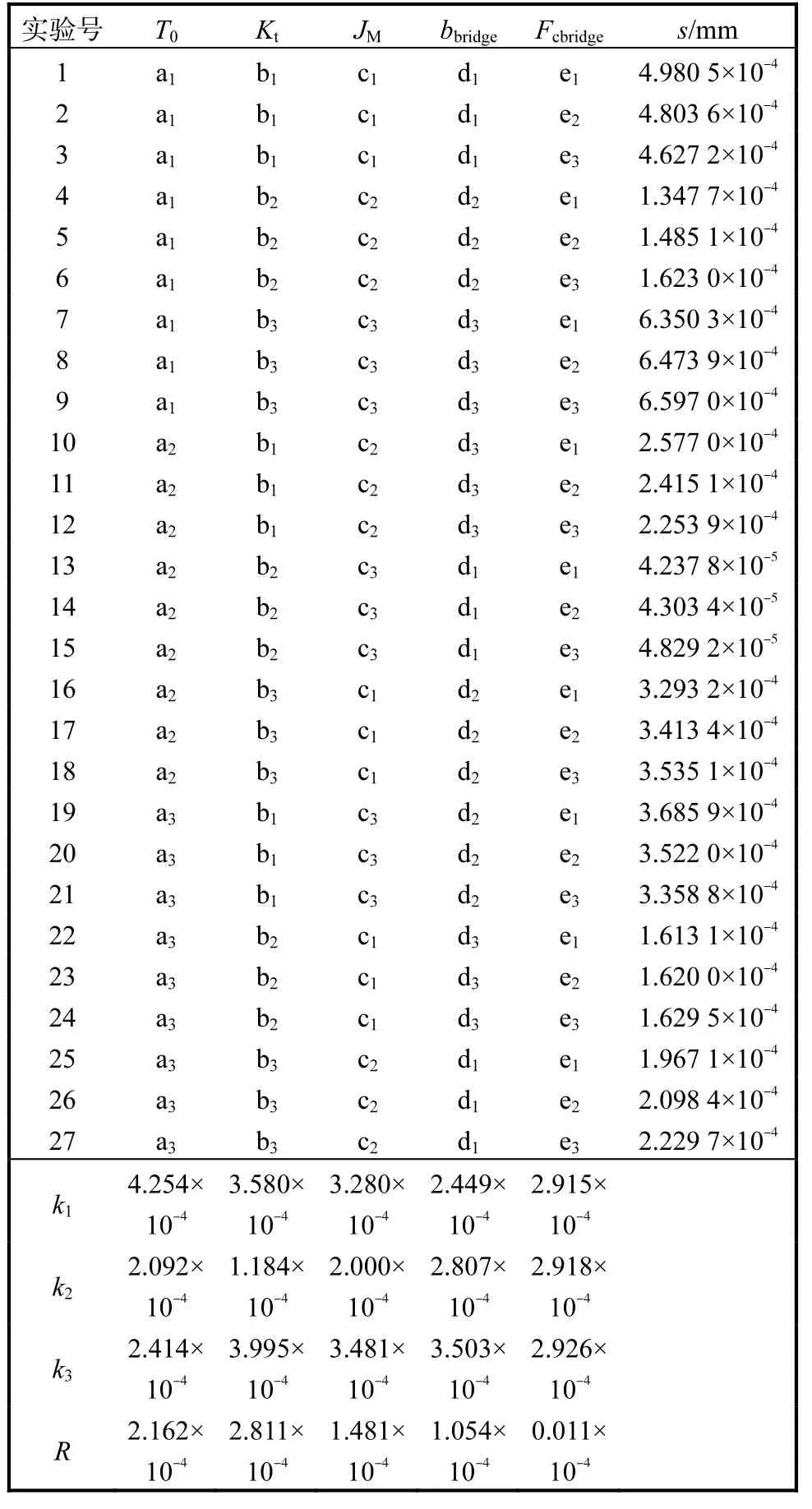
表4 正交实验结果Tab. 4 Orthogonal experiment results

图5 正交实验拟合曲线Fig. 5 Orthogonal test fitting curve
对mcart、bcart、Fcart参数进行辨识需进行x 方向的运动和仿真优化实验.然后按前文中方法对参数进行辨识和优化实验.辨识后的动力学仿真模型参数见表5.为确保所辨识的参数的有效性,进行验证实验,将采集平台和仿真中的运行时间都改为0.8 s,得到验证实验的拟合效果曲线如图6 所示.由图6 可知:验证实验的拟合效果十分理想,证明了所辨识的动力学参数的合理性.根据这组参数进行仿真,能够较好地描述出当前速度下3D 打印头的实际运动情况.

表5 通过实验辨识所得动力学仿真模型参数Tab. 5 Identification of the obtained dynamic simulation model parameters by experiment

图6 验证实验的拟合曲线图Fig. 6 Verification curve of the verification test
5 误差补偿实验
采用基于微分变换的思想,通过将运动参数名义值和真实值之间的微小偏差补偿给控制器的名义参数,从而达到提高定位精度的目的[11].其误差补偿原理如图7 所示,数学模型可表示为
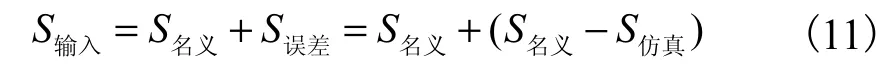

图7 微分变换原理Fig. 7 Principle of differential transformation
按照差分思想进行多次补偿实验,实验中设置相同的运动速度,测量在不同的运动时间内的位移,表6 为进行10 次实验的实验数据.
分析实验数据可以看出,通过补偿后,定位误差有了明显的减小,10 次实验的误差均值由0.064 mm降为0.005 mm,误差补偿起到了显著效果.
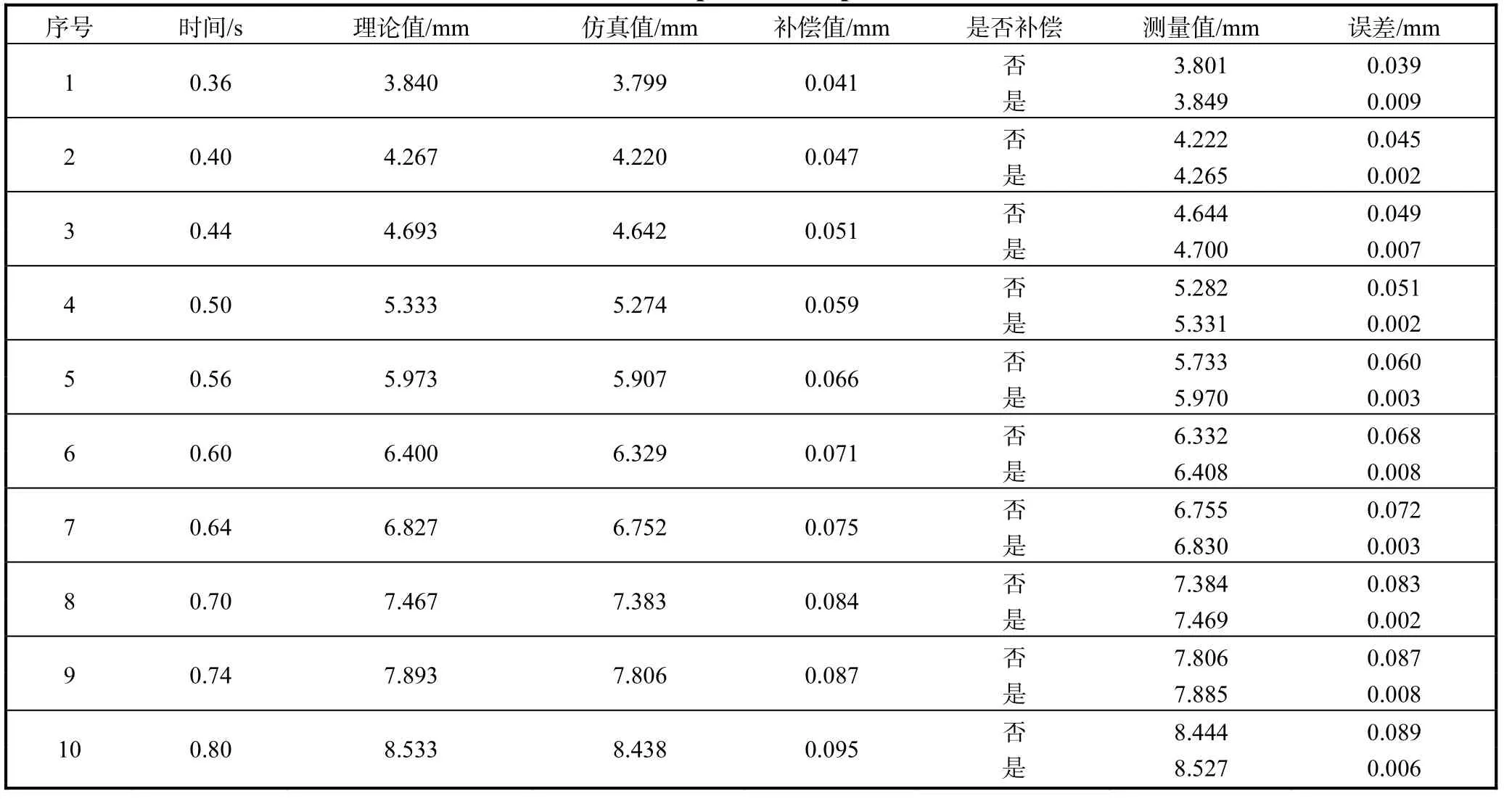
表6 误差补偿实验结果Tab. 6 Error compensation experiment results
6 结 语
本文在充分考虑系统中惯性、摩擦以及弹性形变等可能导致定位误差的因素的基础上,简化运动学模型,通过设计正交实验,对模型参数进行辨识和优化,使仿真结果能够准确贴合实际运动情况,设计了单轴直线运动的误差补偿的算法并进行误差补偿实验,证明了通过对3D 打印机传动机构进行运动学标定和误差补偿可提高其定位精度的有效性和可行性.
