反激式开关电源的电磁干扰建模及抑制方法分析
2021-04-21王京黄猛冯上贤陈宁宁
王京 黄猛 冯上贤 陈宁宁
1.空调设备及系统运行节能国家重点实验室 广东珠海 5190702.珠海格力电器股份有限公司 广东珠海 519070
1 引言
开关电源是典型的非线性控制系统,通过控制半导体开关器件的开通/关断使电源设备进行能量传输[1]。开关电源中包含大量的非线性开关器件,这些开关器件在高频工作过程中会产生丰富的高频电磁骚扰[2,3],对周边控制系统和设备的正常工作带来巨大影响。因此,在机理上对开关电源的EMI进行建模及抑制方法分析具有重要意义[4]。
本文针对常见的反激式开关电源电路进行研究,通过对电路拓扑进行分析,并根据EMI的产生、耦合、传导机理进行建模,得出EMI抑制方法,并针对实际情况予以分析及实验验证,进一步验证了本方法的有效性。
2 反激式开关电源EMI模型分析
2.1 反激式开关电源变压器模型分析
骚扰电压影响源主要为寄生电容所生成的共模及差模电流,这些都是通过开关电源高变化率的电位差所产生的[5],图1示意了寄生电容耦合路径及形式,电流经整流桥、变压器初级、变压器次级与输出电缆间的寄生电容进行流动,进行骚扰电压测试的过程中,这些骚扰电流流过LISN导电回路中的测量电阻,从而在骚扰电压测试结果中体现出来。
其中最主要的骚扰电流是通过变压器的初、次级间的内部寄生电容所产生的,在图中显示为Cw1、Cw2、Cw3、Cw4、Cw5、Cw6。这主要是由于变压器内大面积铜线方向是相反紧密绕制的,绕线匝间会产生一定的寄生电容。例如在开关管Q1工作过程中,由于变压器匝间寄生电容的存在,初级电压的变化会产生一个骚扰电流ip,如公式(1)所示:
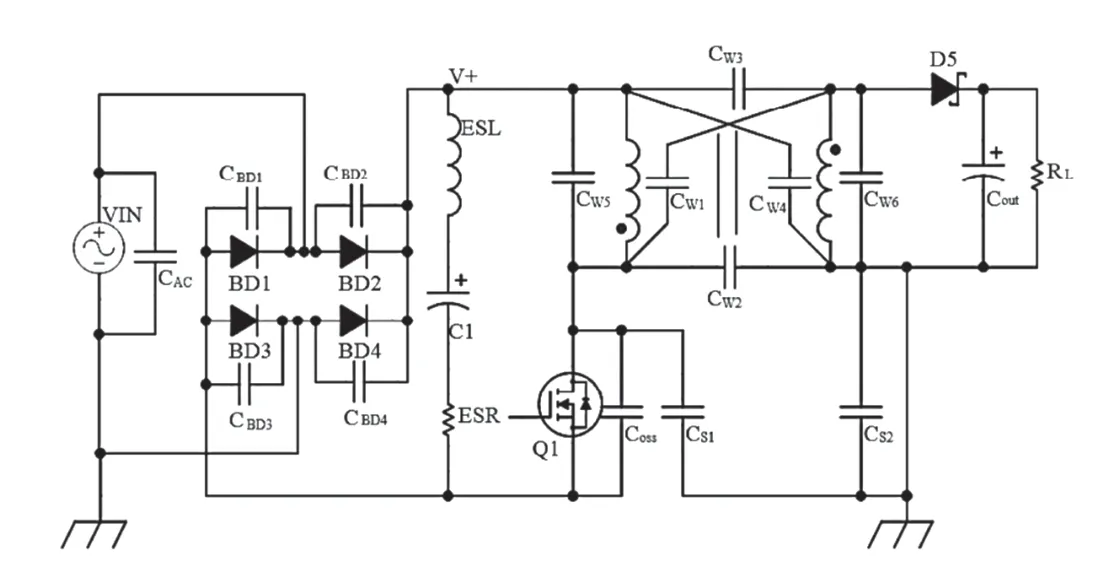
图1 反激式开关电源中电容耦合路径示意

其中:Cw1、Cw2—变压器等效寄生电容(F);U1—开关管漏源电压(V)。
因为变压器中的电压极性变化快速且具有显著差异,所以其产生的骚扰电流大小、方向及路径也各不相同,各骚扰电流之间相互耦合、相互作用[6]。依此特性设计变压器,可以从骚扰电流的互相抑制角度降低EMI释放。经调整变压器中的线圈结构或者外接抑制电磁干扰用电容器的方式改变原有寄生电容结构参数,控制寄生电容骚扰电流耦合路径。这些寄生产生的骚扰电流的幅度比变压器工作电流要小很多,因此EMI的控制与改变能够在不影响变压器其他电气参数的情况下来达到[7]。
图2示意了变压器寄生电容结构,初级绕组与次级地线之间寄生电容—C12m,辅助绕组与次级地线之间寄生电容—Ca2m,补偿绕组与次级地线之间寄生电容—Ck2m,次级绕组与初级地线间寄生电容—C21m,初级地线与次地线之间寄生电容—C2m21m。由此,将图2做进一步简化,可得到图3的变压器简化模型。
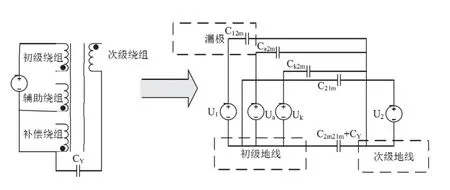
图2 变压器寄生电容示意
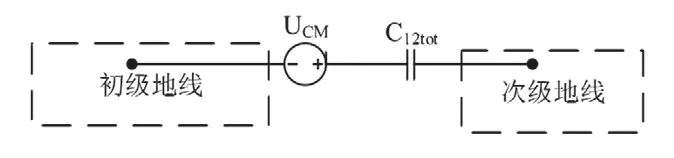
图3 变压器初次级简化模型
定义变压器初级地线与次级地线之间的寄生骚扰电压为UCM,初级地线与次级地线之间的等效总寄生电容为C12tot,初级地线与次级地线寄生总电容产生的电荷量为ΔQ,UCM可通过公式(2)表达:
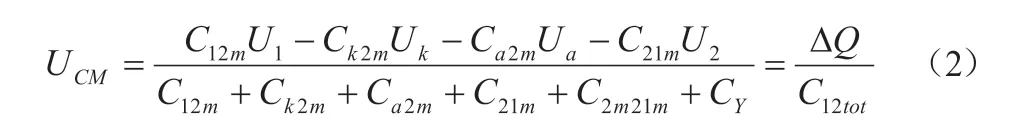
可得公式(3):
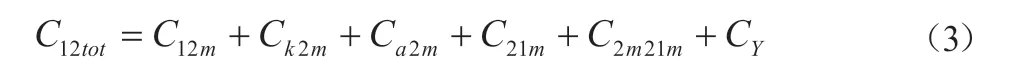
对上述两个公式进行分析,通过增大初级和次级之间的外部电容CY的容值,C12tot会随之增大,初级地线与次级地线之间产生出的骚扰电压将随之减小,反之UCM将增大。
2.2 开关电源骚扰电压测试模型及验证
图4中ILI即LISN中检测电阻上的电流,C1mL、C1mN、CD即整流桥二极管的等效寄生电容,RmL与RmN构成了LISN内的检测阻抗,C12tot即变压器等效寄生电容,Uc即变压器的骚扰电压,Ud为相对大地的等效电压。
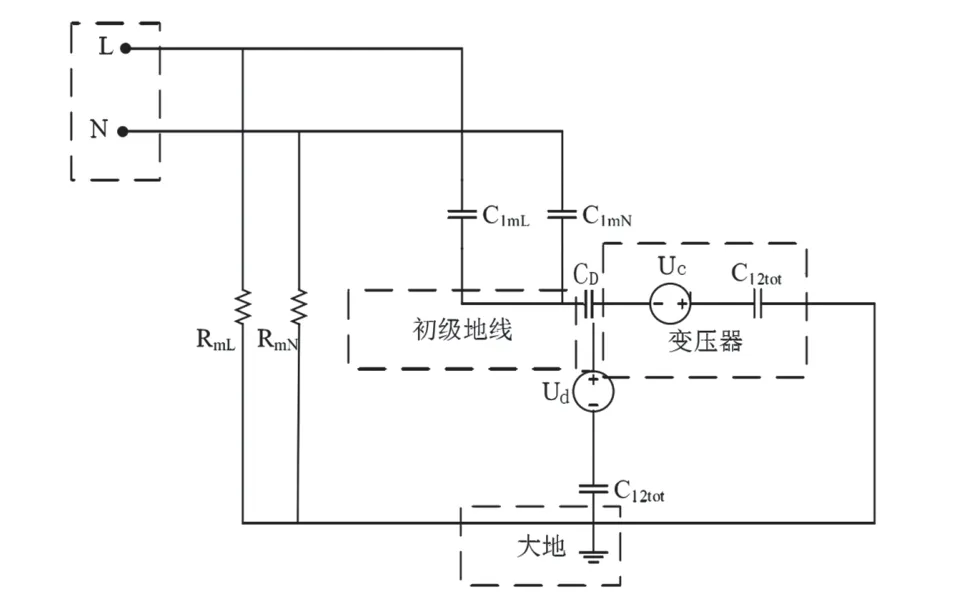
图4 骚扰电压测试模型
在整流二极管不导通状态下,LISN检测到的骚扰电流IL1如下述公式(4):
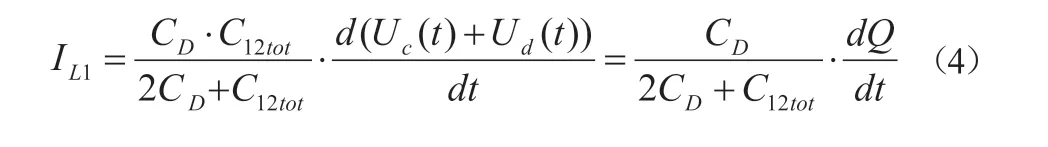
在整流二极管导通的状态下,LISN检测到的骚扰电流IL1如下述公式(5):
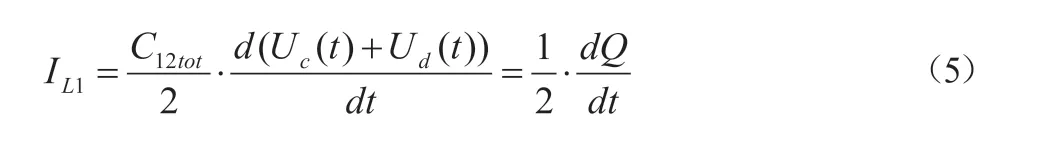
通过公式(4)、(5)能够分析出变压器寄生电容产生的骚扰电压对LISN接收到的骚扰电流起到决定性作用。
为进一步分析变压器寄生电容参数与骚扰电压的关系,在仿真软件中对变压器的寄生电容值进行设置,并对骚扰电压进行傅里叶变换分析,骚扰电压仿真电路模型如图5所示。
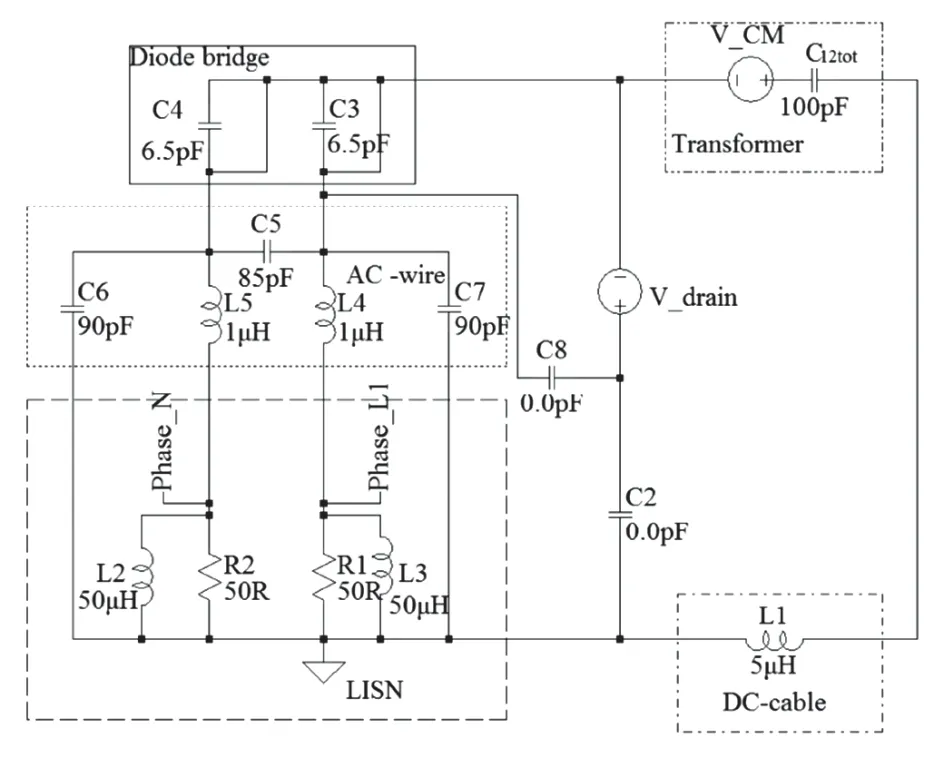
图5 骚扰电压测试仿真电路模型
图6为C12tot在100 pF状态下LISN检测到的骚扰电压,图7为图6骚扰电压的傅里叶变换波形。
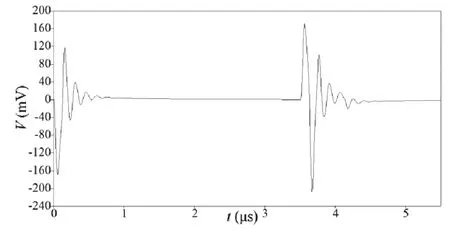
图6 C12tot=100 pF状态下LISN接收到的骚扰电压波形
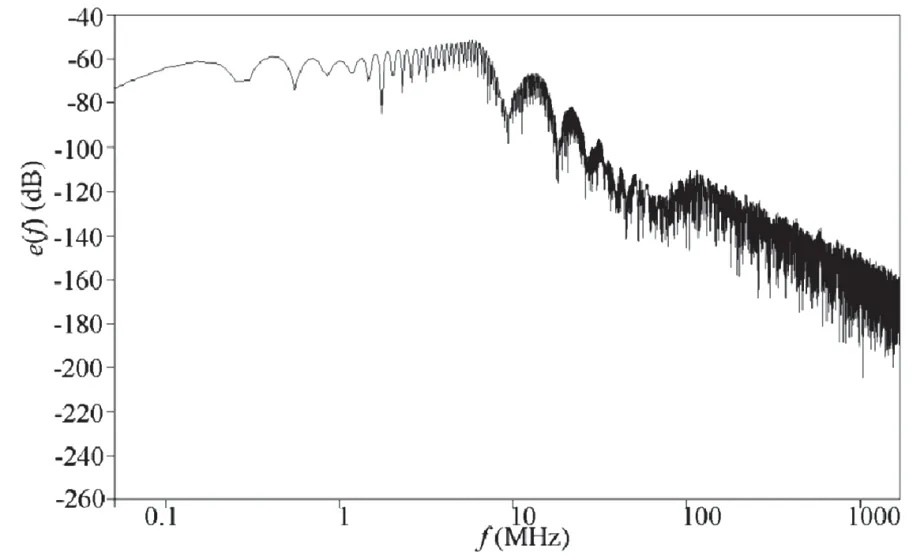
图7 C12tot=100 pF状态下LISN接收到骚扰电压的傅里叶变换
图8为C12tot为10 pF状态下LISN检测到的骚扰电压,图9为图8骚扰电压的傅里叶变换波形。
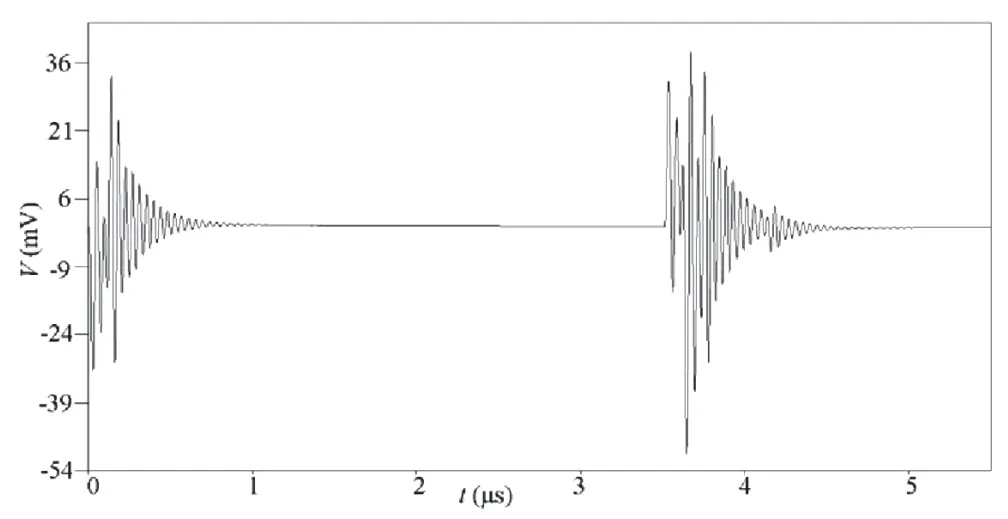
图8 C12tot=10 pF状态下LISN接收到的骚扰电压波形
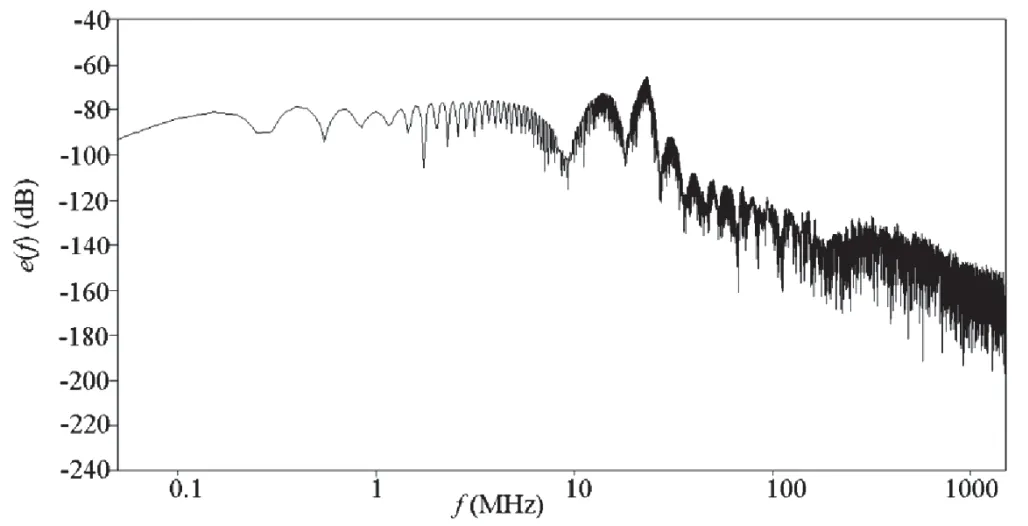
图9 C12tot=10 pF状态下 接收到骚扰电压的傅里叶变换
经图6与图8对比得出C12tot值的变化对LISN接收到的骚扰电压会产生影响,振荡波形出现显著变化,由图7与图9的傅里叶变换波形能够进一步确认该结论。
为验证公式(2)及公式(3)中CY与UCM的关系,在仿真软件中对图5电路模型进行更改,在变压器的初、次级之间增加电容C9,对变压器的寄生电容进行原理上的补偿,并对骚扰电压进行傅里叶变换分析,骚扰电压仿真电路模型如图10所示。
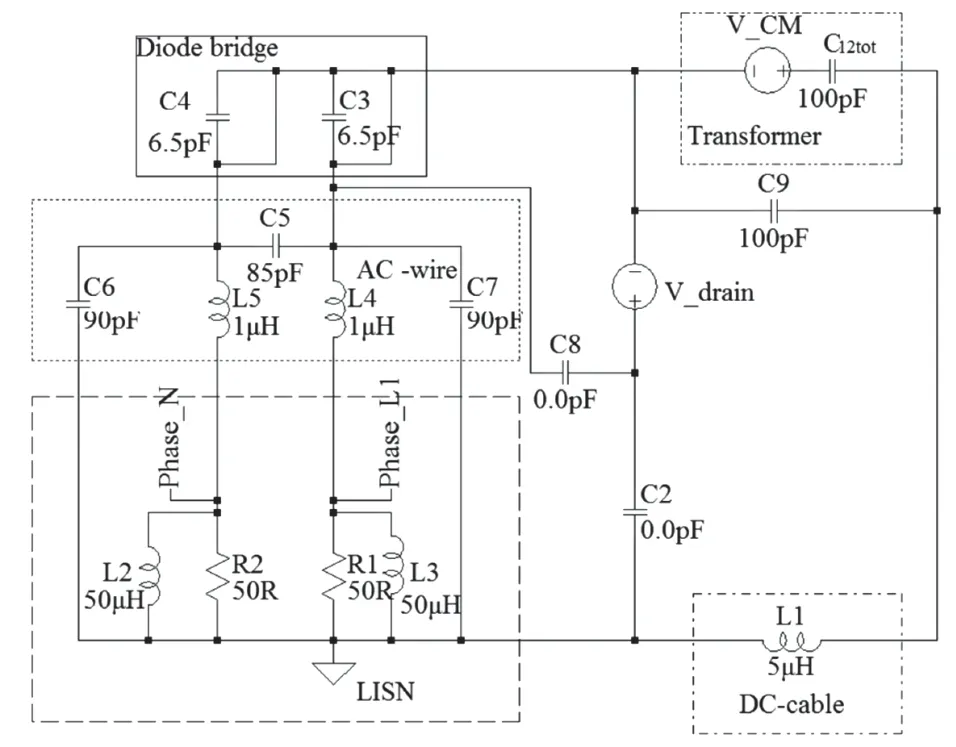
图10 变压器初次级间增加100 pF电容的测试电路模型
图11为变压器初、次级之间增加100 pF电容C9后LISN接收到的骚扰电压波形,图12为图11骚扰电压的傅里叶变换波形。
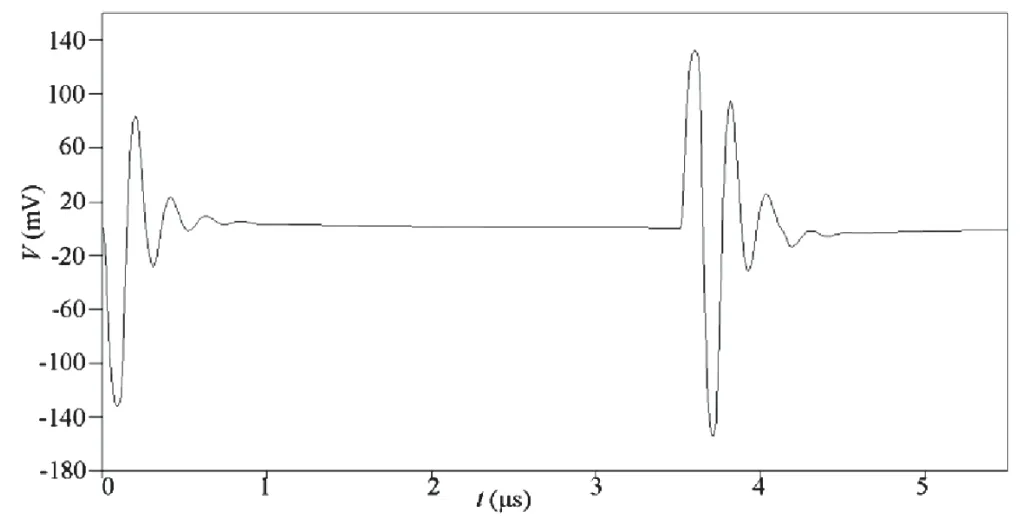
图11 变压器初次级间增加100 pF电容 LISN接收到的骚扰电压
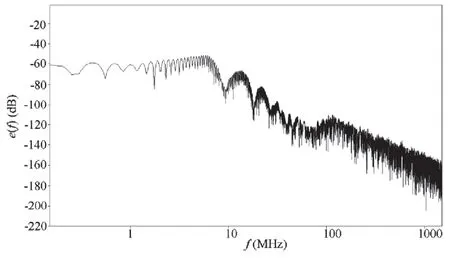
图12 变压器初次级间增加100 pF电容LISN接收到骚扰电压的傅里叶变换
经图6与图11对比得出变压器初、次级之间增加电容C9对LISN接收到的骚扰电压会产生影响,振荡波形出现显著变化,由图7与图12的傅里叶变换波形能够进一步确认该结论。
经仿真验证,变压器寄生电容C12tot的大小对反激式开关电源的骚扰电压具有重要影响,可以通过改变变压器原有寄生电容的大小来改善EMI效果。也可以通过在变压器初次级之间增加电容的方式改变原有寄生电容的耦合路径,减小整体寄生电容的方式对EMI效果进行改善。
3 干扰的抑制与验证
根据提出的反激式开关电源EMI模型以及对EMI的抑制方法,使用一款反激式开关电源控制器进行对比测试验证,电源实物如图13所示。在3米法半电波暗室对该电源进行EMI测试,测试数据超标严重,测试数据如图14所示。基于本文提出的EMI模型进行分析,通过对骚扰源进行定位,对变压装置寄生电容参数进行计算,对变压装置初次级耦合及传导路径进行分析,得出抑制方法。通过在变压装置初次级之间增加1 nF的电容,可以为骚扰源构造新的回流路径,并对原变压器寄生电容进行补偿,减小变压器整体耦合电容,整体起到了良好的EMI抑制效果。EMI模型分析如图15所示,按照上述EMI抑制方法进行抑制,测试数据合格,测试数据如图16所示。

图13 反激式开关电源实物
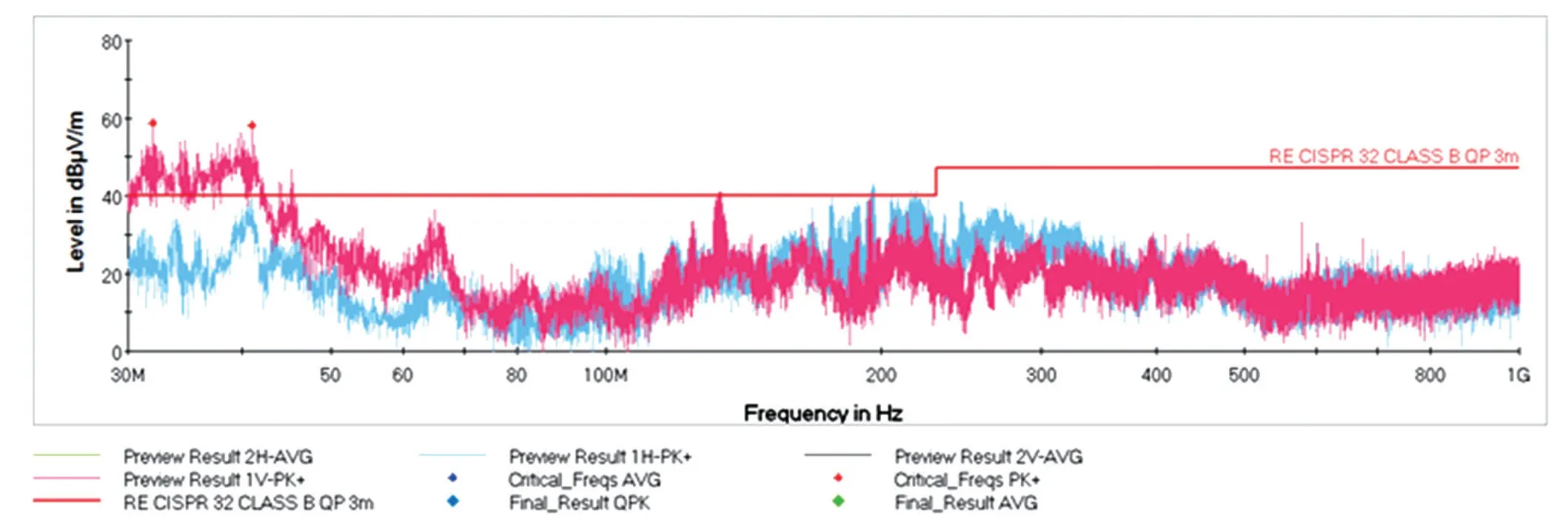
图14 反激式开关电源EMI测试波形
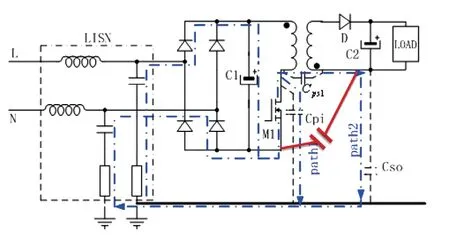
图15 EMI模型分析
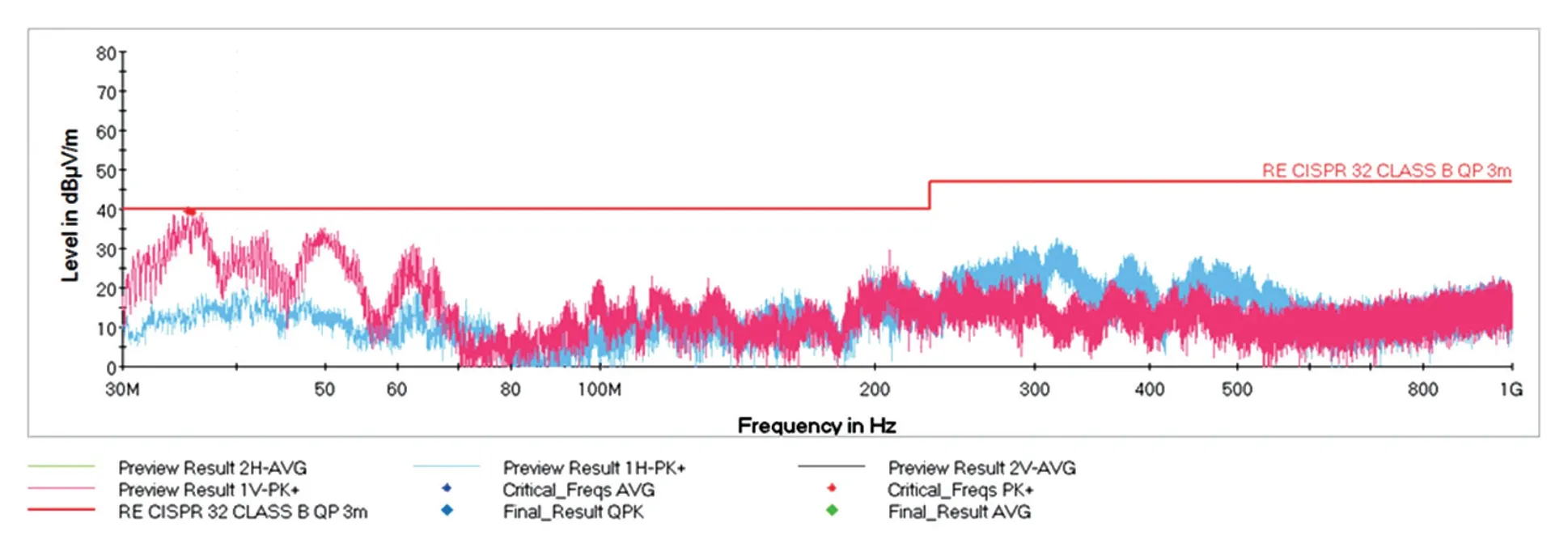
图16 反激式开关电源EMI测试波形(抑制后)
4 结论
综上所述,反激式开关电源变压器中的寄生电容对EMI影响巨大,通过减小变压器总寄生电容值可以对EMI效果进行有效改善。由于变压器原始寄生电容随着变压器的成型已为确定状态,因此在应用层面上通过在变压器初次级间增加电容的处理方式,额外增加的电容可以为骚扰信号提供新的回流路径,对变压器的固有寄生电容起到补偿作用,从而改善开关电源的EMI表现效果。本研究最后使用典型的反激式开关电源实物对所提出的模型及EMI抑制方法进行分析及测试验证,数据表明,达到了理想的EMI抑制效果。由于电路的寄生参数在实际应用中差异较大,且随着频率的提升,寄生器件的性质与参数也会随之变化,增加了分析的不确定性,因此,在实际的应用中还需要依据实验数据做更全面的分析。
