基于SOA-SVM和SOA-BP模型的溶解氧预测

张学坤

(云南省水文水资源局西双版纳分局,云南 景洪 666100)

溶解氧(DO)是反映水质状况及自净能力的重要指标。提高溶解氧预测精度对于保护水资源、水环境、水生态以及保障饮用水安全具有重要意义。目前，用于溶解氧预测的方法有BP神经网络[1]、GRNN[1]、Elman[1-2]、RBF[3]、NARX神经网络[4]、回归支持向量机(SVR)[5]、极限学习机(ELM)[6]、组合预测法等[7]，均具有较好的预测效果。为进一步提高溶解氧预测精度，拓展现有预测模型及方法，本文研究提出一种基于海鸥优化算法(Seagull Optimization Algorithm，SOA)与支持向量机(Support Vector Machines，SVM)及BP神经网络相融合的溶解氧预测模型，分别利用SOA对SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权阈值进行优化，建立SOA-SVM、SOA-BP溶解氧预测模型；基于云南省西双版纳州国家重要供水水源地景洪电站2009年1月至2020年9月共141组逐月溶解氧监测数据，通过自相关函数法(autocorrelation function method，AFM)、虚假最邻近法(false nearest neighbor，FNN)设置4 种方案，利用SOA-SVM、SOA-BP模型对实例4种方案溶解氧进行预测，预测结果与SVM和BP模型进行对比，旨在验证SOA-SVM、SOA-BP模型用于溶解氧预测的可行性。本文研究意义和价值在于：介绍了新颖的海鸥优化算法(SOA)，利用SOA分别优化SVM惩罚因子等关键参数和BP神经网络权阈值，构建SOA-SVM、SOA-BP模型，并将模型用于溶解氧实例预测，不但拓展了SVM、BP模型的优化方法，而且为溶解氧等相关预测研究提供借鉴。

1 研究方法

1.1 海鸥优化算法(SOA)

海鸥优化算法(SOA)是Gaurav Dhiman等[8]于2019年提出的一种新型元启发式优化算法，其灵感来源于自然界海鸥迁徙和攻击行为。与其他算法相比，SOA收敛速度快、寻优精度高、调节参数少，具有较好的寻优精度和全局搜索能力。

SOA主要基于以下优化策略：①海鸥成群迁徙，为避免彼此碰撞，海鸥初始位置不同；②海鸥向最适合生存的海鸥方向行进，即向具有最佳适应度值的海鸥方向行进；③依据最佳海鸥适应度值更新其他海鸥位置。参考文献[8]，SOA数学描述简述如下。

a)初始化。与大多数元启发式算法类似，SOA通过初始化海鸥种群来启动优化过程，即在搜索空间范围初始化海鸥位置：

(1)

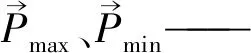
b)海鸥迁徙策略。SOA通过3个阶段完成海鸥迁徙过程，即避免冲突阶段、向最佳海鸥飞行阶段和保持靠近最佳海鸥阶段。

避免冲突阶段。海鸥在迁徙过程中为避免与其他海鸥发生碰撞，通过附加变量A来计算新海鸥位置，数学描述如下：

(2)

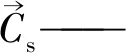
向最佳海鸥飞行阶段。在避免海鸥群体间碰撞后，当前海鸥向着具有最佳适应度值的海鸥方向飞行，数学描述如下：

(3)

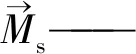
保持靠近最佳海鸥阶段。迁徙过程中，当前海鸥依据最佳海鸥适应度值更新其位置，数学描述如下：

(4)

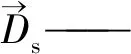
c)海鸥攻击策略。海鸥在迁徙过程中不断改变攻击角度和速度，并通过螺旋飞行方式攻击猎物，位置更新数学描述如下：

(5)

式中x、y、z——平面坐标，其中x=r×cos(k)，y=r×sin(k)，z=r×k，r=u×ekv；r——螺旋线旋转半径；k——[0，2π]内的随机数；u、v——螺旋形状常数；e——自然对数底数。

1.2 支持向量机

设含有l个训练样本的集合为{(xi，yi)，i=1，2，…，l}，xi(xi∈Rd)为第i个训练样本输入列向量，yi∈R为对应输出值[9-12]。则SVM在高维特征空间中建立的线性回归函数为：

f(x)=wΦ(x)+b

(6)

式中Φ(x)——非线性映射函数；w——超平面的法向量；b——超平面的偏移量。

最终回归函数为：

(7)

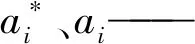
选择径向基核函数作为SVM核函数，径向基核函数表达式为：

(8)

式中g>0。

1.3 BP神经网络

设典型3层BP神经网络输入维数为m、隐层为l、输出维数为1，参考相关文献[13-16]，BP神经网络完成映射的数学表达式可表示如下：

(9)

式中lj——隐层到输出层的连接权值；bj——隐层节点的输出；ε——隐出层的阈值。

采用Sigmoid函数的隐层节点输出表示如下：

(10)

式中ωij——输入层至隐层的连接权值；θj——隐层节点的阈值。

1.4 预测实现步骤

步骤一利用SOA优化SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权阈值，建立SOA-SVM、SOA-BP预测模型；采用自相关函数法(AFM)、虚假最邻近法(FNN)构建4 种方案的输入输出向量，划分训练样本和预测样本，利用处理后的训练样本对SOA-SVM、SOA-BP模型进行训练。

步骤二确定待优化适应度函数。本文选用训练样本与实测值均方误差构建适应度函数，描述如下：

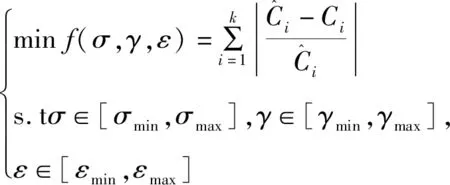
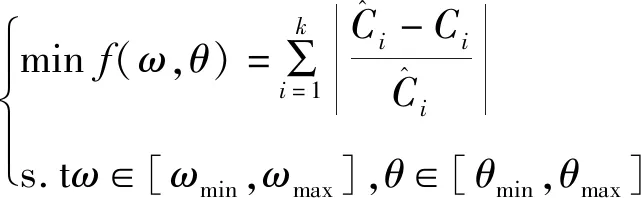
(11)

步骤三参数设置。设置海鸥群体规模N、最大迭代次数T、算法终止条件、频率系数fc=1和SVM关键参数和BP神经网络权阈值搜索范围，利用式(1)随机初始化海鸥位置，令当前迭代次数m=0。

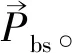
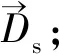
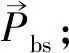
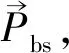
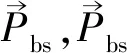
2 应用实例

2.1 数据来源

景洪电站位于云南省澜沧江下游河段，西双版纳州景洪市境内，为国家重要供水水源地和景洪市城区主要供水水源。电站坝址以上集水面积14.91万km2，州内集水面积3 071 km2，多年平均径流量571亿m3，州内库区水面面积21.75 km2，河长65.5 km，正常蓄水位为602 m，相应库容8.7亿m3，设计供水人口19.6万人，现状年供水量约2 000万m3。景洪电站为云南省重点湖库水生态监测站，西双版纳州水环境监测分中心于2009年1月起对景洪电站水质进行取样检测，年监测 12次，为每月监测。

2.2 输入输出向量

数据来源于景洪电站2009年1月至2020年9月共141组逐月溶解氧监测成果，利用自相关函数法(AFM)、虚假最邻近法(FNN)设置4 种方案进行溶解氧预测，具体如下。

a)方案一至方案三。利用AFM法计算该实例延迟时间为1～10的自相关系数分别为0.465、0.435、0.319、0.173、0.154、0.123、0.116、0.180、0.190、0.295。可见，当延迟时间为1～3时自相关系数最大，分别为0.465、0.435、0.319。因此，方案一采用前1 个月的溶解氧预测下1个月的溶解氧；方案二采用前2个月的溶解氧预测下1个月的溶解氧；方案三采用前3个月的溶解氧预测下1个月的溶解氧。

b)方案四。采用AFM和FNN法确定方案四延迟时间为1、嵌入维数为6，即采用前6个月的溶解氧预测下一个月的溶解氧。

对于上述方案一至方案四，本文利用实例2009年1月至2018年12月溶解氧监测数据作为训练样本，2019年1月至2020年9月溶解氧监测数据作为预测样本。

2.3 参数设置

a)SOA-SVM模型。设置SOA最大迭代次数T=100，种群规模N=50，频率系数fc=1，其他采用SOA默认值；选择径向基核函数为RBF，惩罚因子σ、核函数参数γ、不敏感系数ε搜索范围分别为[0.01,100]，[0.1,100]，[0.001,0.1]，交叉验证折数V=5，采用[-1,1]对原始数据进行归一化处理。

b)SOA-BP模型。设置SOA最大迭代次数T=100，种群规模N=50，频率系数fc=1，其他采用SOA默认值；设置方案一至方案四的BP神经网络隐层数分别为4、6、8、11，隐含层和输出层传递函数分别采用logsig和purelin，训练函数采用traingdx，设定期望误差0.01,最大训练轮回1 000，采用[-1,1]对原始数据进行归一化处理。

c)SVM和BP模型。通过试凑法确定SVM模型的惩罚因子σ、核函数参数γ、不敏感系数ε；BP模型的网络结构、隐含层数、传递函数、训练函数、期望误差、最大训练轮回次数均与SOA-BP模型相同；SVM、BP模型均采用[-1,1]对原始数据进行归一化处理。

2.4 预测结果及分析

建立SOA-SVM、SOA-BP、SVM、BP模型对实例方案一至方案四的溶解氧进行训练及预测，并选取平均相对误差绝对值MRE(%)、平均绝对误差绝对值MAE(mg/L)、最大相对误差MaxRE(%)作为评价指标。4种模型不同方案的预测结果见表1；4种方案的溶解氧预测相对误差效果见图1—4。

表1 方案一至方案四不同模型溶解氧预测结果及其对比

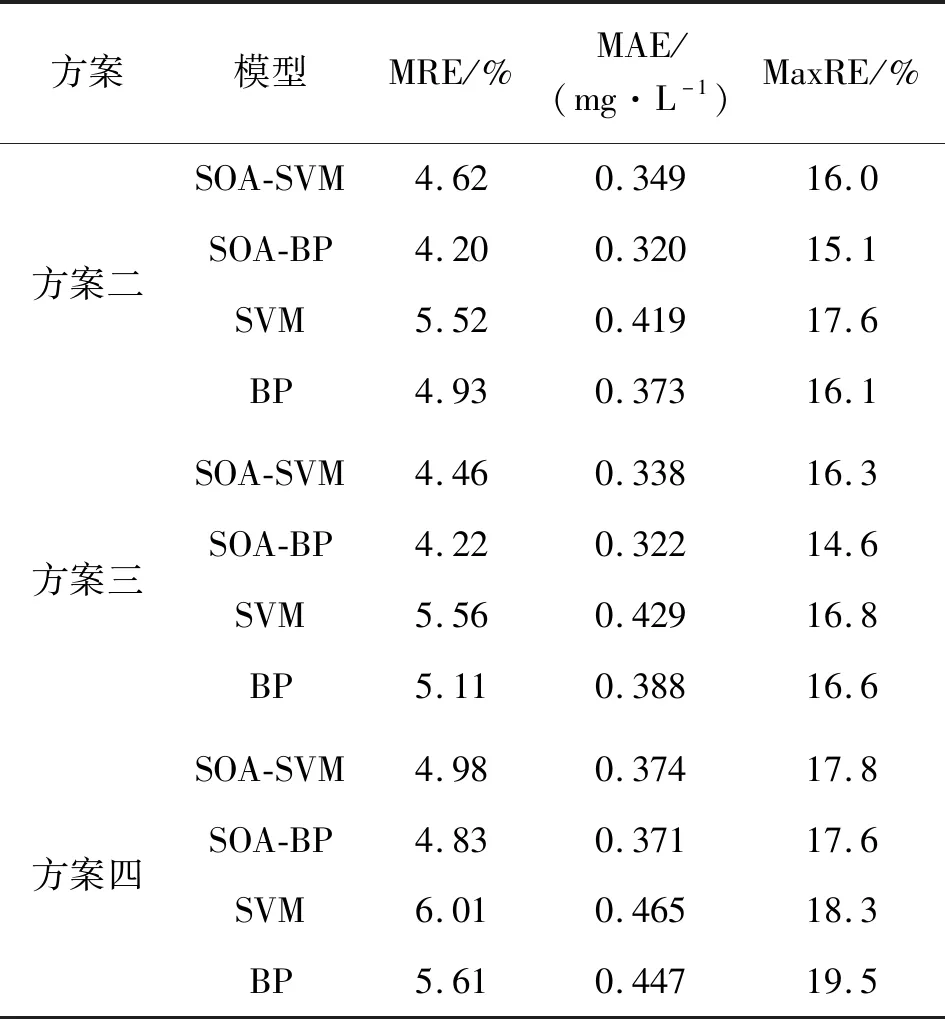
续表1 方案一至方案四不同模型溶解氧预测结果及其对比

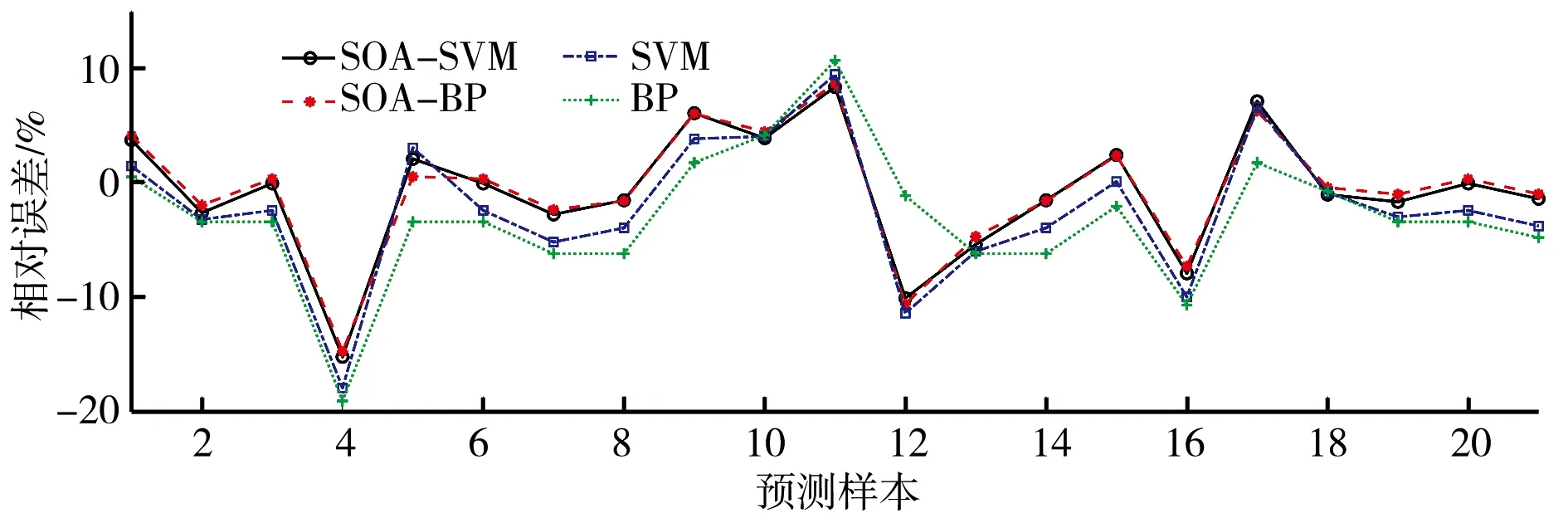
图1 方案一预测结果相对误差

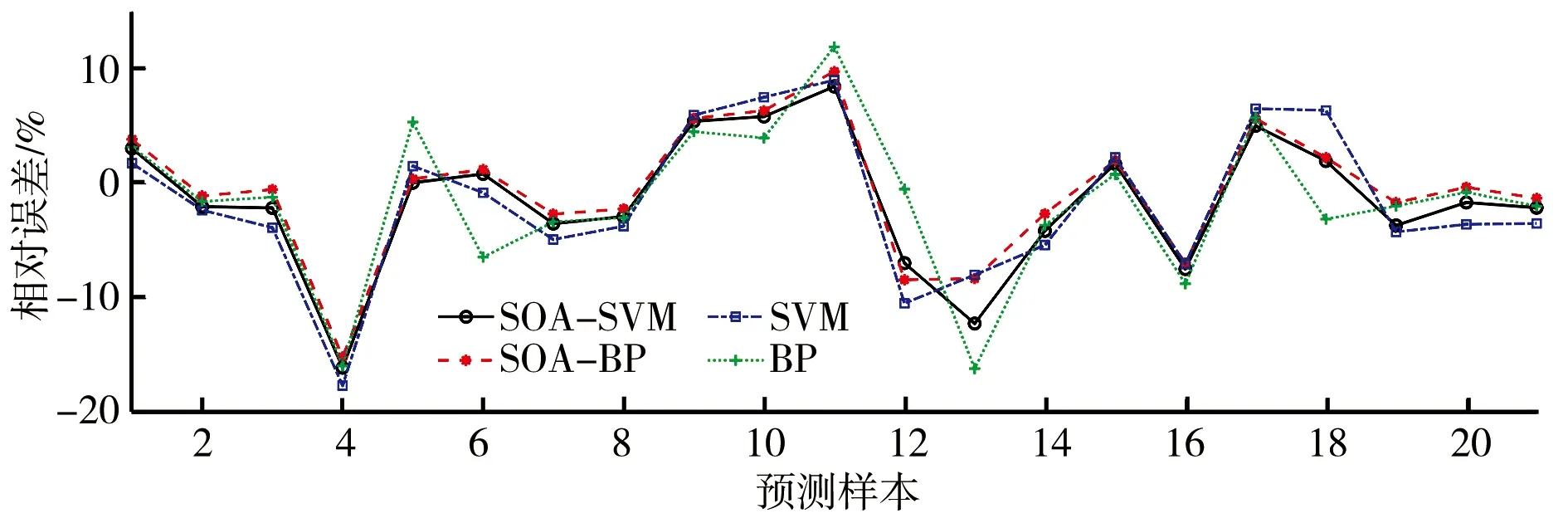
图2 方案二预测结果相对误差

图3 方案三预测结果相对误差

图4 方案四预测结果相对误差

依据表1及图1—4可以得出以下结论。

a)SOA-SVM、SOA-BP模型对方案一至方案四溶解氧预测的平均相对误差绝对值分别在4.07%～4.98%、3.85%～4.83%之间，平均绝对误差绝对值分别在0.309～0.374、0.294～0.371 mg/L之间，预测精度均优于SVM、BP模型，具有较好的预测效果，表明SOA能有效优化SVM惩罚因子、核函数参数、不敏感系数以及BP神经网络权阈值，SOA-SVM、SOA-BP模型用于溶解氧预测是可行的。SOA-BP模型的预测精度要优于SOA-SVM模型。

b)对于SOA-SVM和SVM模型，SOA-SVM模型对方案一至方案四溶解氧预测的平均相对误差绝对值分别为4.07%、4.62%、4.46%、4.98%，预测精度分别较对应方案的SVM模型提高18.9%、16.3%、19.8%、17.1%，表明采用SOA寻优SVM惩罚因子、核函数参数、不敏感系数，不但省去人工试凑的繁琐，而且大大提高溶解氧的预测精度。

c)对于BP神经网络结构、隐含层数等完全相同的SOA-BP和BP模型，SOA-BP模型对方案一至方案四溶解氧预测的平均相对误差绝对值分别为3.85%、4.20%、4.22%、4.83%，预测精度分别较对应方案的BP模型提高21.6%、14.8%、17.4%、13.9%，表明采用SOA寻优BP神经网络权阈值能有效提高溶解氧的预测精度。

d)不同方案的预测精度为：方案一>方案二>方案三>方案四。对于方案一至方案三，其自相关系数越大，预测精度越高；通过AFM、FNN法确定延迟时间和嵌入维数构建的方案四未能获得理想的预测效果。

3 结论

本文将SOA与SVM、BP 神经网络方法相结合，构建SOA-SVM、SOA-BP溶解氧预测模型。利用云南省西双版纳州国家重要供水水源地景洪电站2009年1月至2020年9月逐月溶解氧监测数据进行模型构建与验证，并分别采用4种方案对逐月溶解氧进行预测，得出以下结论。

a)SOA-SVM、SOA-BP模型对实例方案一至方案四的溶解氧预测精度均优于SVM、BP模型，具有较好的预测效果和精度；SOA能有效优化SVM关键参数和BP神经网络权阈值，SOA-SVM、SOA-BP模型用于溶解氧预测是可行的。SOA-BP模型预测精度要优于SOA-SVM模型。

b)对于SVM、BP模型，分别采用SOA寻优惩罚因子、核函数参数、不敏感系数以及网络权阈值，不但省去人工试凑或调试的繁琐，而且大大提高溶解氧的预测精度，具有一定的实际应用价值。

c)不同方案的预测精度为方案一>方案二>方案三>方案四。