基于Copula函数的降雨随机模拟方法在古黄河流域的应用

潘奇鑫，李 帆，刘 萍，李春秀

(扬州大学水利科学与工程学院，江苏 扬州 225009)

在极端气候频繁出现的背景下，中国洪涝、干旱灾害频发，防范洪涝、干旱灾害的任务变得越来越严峻。自唐以来，江苏地区就是全国经济发达的地区之一，也是自然灾害频发的地区，尤以洪涝、干旱灾害最为显著[1]。中长期水文预报作为预防灾害的有效手段之一，在近些年得到了广泛的应用，其对水库合理调度、防洪减灾、水资源利用有着重要意义。而现阶段的水文预报大多具有确定性，回避了预报值的不确定性，无法满足对风险信息的需求。以概率的形式定量分析水文预报不确定性，据此做出的概率水文预报，不仅在理论上更加科学，而且在实践应用中能产生更高的效益，是水文预报技术发展的必然趋势。张铭等[2]采用贝叶斯概率水文预报系统在中长期径流预报中提高水文预报的精度。中长期概率预报不仅可得到比确定性预报更高的精度，而且还能为决策者提供更丰富的预报信息[3]。

相对于传统的水文频率研究方法，Copula函数法具有“连接”的功能[4]，且计算过程简便灵活，同时适用于边缘分布相同与不同的联合分布，也适用于多维的联合分布，且效果相对较好，基本能解决传统水文频率研究方法中存在的问题。起初，Copula函数主要在金融、保险等领域运用，自2003年起Copula函数才开始在水文频率计算方面展开研究[5]。阳艾利等[6]研究表明，Gumbel Copula函数可用于降雨量和径流量联合分布的拟合；陈心池等[7]研究表明，Frank Copula函数可用于汉江中上游流域极端降雨洪水三维联合分布拟合。彭杨等[8]基于多维Copula函数进行日含沙量过程随机模拟，模拟结果表明，该法能保持实测日含沙量的主要统计特性，模拟序列与实测序列的统计特征值吻合良好。李帆等[9]基于Archimedean Copula函数对淮河月径流进行随机模拟，研究结果表明，Archimedean Copula函数结合Gibbs采样可有效建立相邻月份间的相关性结构。

相对于传统的单一站点预报，通过协整理论建立多站点时空关系，并运用非线性关系进行联合预报的多站点同步预报方式，具有更为突出的预报效果。吴金冉等[10]以青海省海东和果洛月降水量数据为例，得出结论：多站点同步预报模型，相对于传统单站点预报模型具有更为突出的预报效果。

本文以江苏省宿迁市古黄河流域典型站点实测降雨量为研究对象，基于Copula函数[11]进行3个站点两两间月降雨量联合分布拟合，并结合Gibbs抽样法[12]，实现月降雨量随机模拟。通过比较实测和模拟月降雨量，对模拟结果的有效性进行验证，为多站点间的中长期概率水文预报提供参考。

1 数据与方法

1.1 数据来源

宿迁市位于江苏省北部。古黄河是宿迁市主要河流之一，其横穿宿迁市城区中部，全长114.3 km。流域面积约296.9 km2。古黄河流域属于暖温带季风性气候，四季分明，年际降雨量变化较大，且年内分布不均，易形成春旱、夏涝、秋冬干天气。多年平均降水量为913.1 mm。多年汛期平均降雨量611.5 mm，约占多年年平均降雨量的67.0%，最大汛期降雨量1 256.0 mm(2003年)，最小降雨量283.1 mm(1966年)。本文选取分布于古黄河流域上、中、下游的宿迁闸站、刘老涧站、新袁闸站3个代表站(图1)39年(1980—2018年)月实测降雨量资料作为研究对象。

图1 研究区域及站点分布

1.2 二维Copula函数理论

Copula函数的种类较多，常用的有椭圆Copula函数中的Gaussian Copula函数和Archimedean Copula函数中的Gumbel Copula、Clayton Copula、Frank Copula函数[13]。其中Archimedean Copula函数因其适用性强，构造简单、计算简便，应用十分广泛。

常用二维Archimedean Copula函数如下：

Gumbel CopulaC(u,v)=e-[(-lnu)θ+(-lnv)θ]1/θ

(1)

Clayton CopulaC(u,v)=(u-θ+v-θ-1)-1/θ

(2)

(3)

Copula 函数的参数估计方法有很多[14]，目前较常用的有非参数法和两阶段估计法[15]，本文采用非参数法进行参数求解。

非参数法通过构建Kendall秩相关系数τ与Copula函数参数θ间相关关系来求解参数：

(4)

(5)

(6)

1.3 分布函数优选

本文选取P-III型分布、指数分布和Gamma分布作为待选边缘分布。通过计算各边缘分布均方根误差来选取最优分布，并通过 Kolmogorov-Simirnov检验(K-S检验)对样本进行拟合优度检验。再选取Gumbel Copula、Clayton Copula、Frank Copula函数为备选函数建立模型，通过Kendall秩相关系数τ与式(4)—(6)，计算相关参数。采用赤池信息法(Akaike Information Criterion，AIC)[16]优选Copula 函数模型，AIC最小为最优。

2 流域内站点间月降雨量联合分布模型建立

2.1 各站降雨量边缘分布确定

目前，中国水文计算分析中常常假定降雨、径流服从的最优分布为P-III分布。但实际情况中，P-III型分布并非具有普适性。在Copula函数中，选取拟合优度最好的边缘分布，是决定联合分布模型拟合精度的关键因素之一。因此，选取P-III型分布、指数分布和Gamma分布作为待选边缘分布，通过计算各边缘分布均方根误差来选取最优分布(表1)。

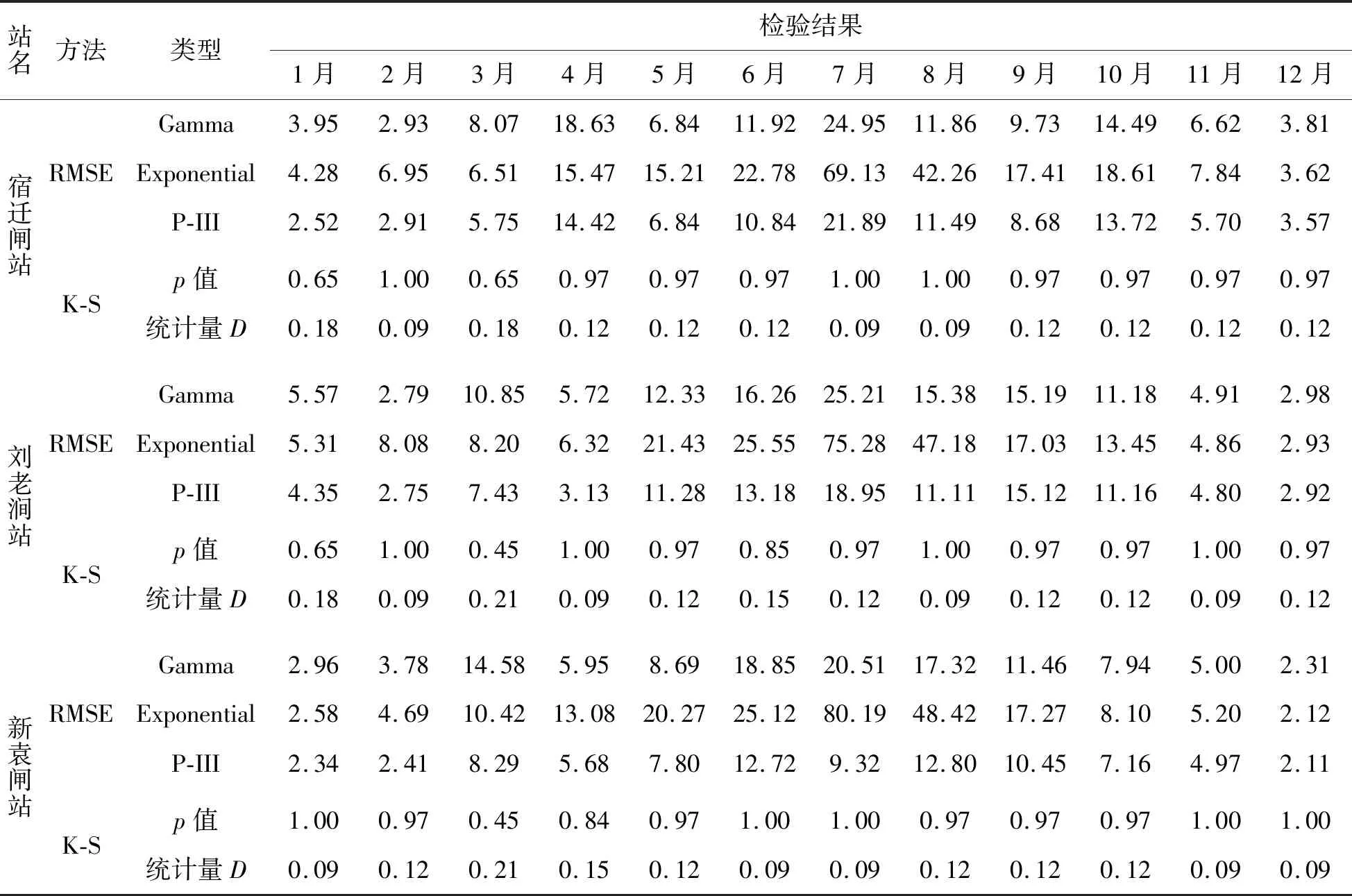
表1 边缘分布拟合优度检验结果

由表1可知，根据RMSE最小准则，3个站点1—12月降雨变化P-III分布拟合的RMSE值较Gamma分布和Expoerntial分布小，因此，选取P-III分布作为宿迁闸站、刘老涧站、新袁闸站月尺度降雨变化的边缘分布。其中，K-S检验值均大于0.05，统计值均小于临界值，故认为通过检验。

2.2 Copula函数的选择

本文以Archimedean Copula函数中的Gumbel Copula、Clayton Copula、Frank Copula作为备选函数建立联合概率分布函数。由Gumbel Copula逻辑模型的结构可知，其适用于两变量之间存在正相关关系的序列；Clayton Copula函数一般适用于有正相关关系的随机变量；Frank Copula函数适用于正负相关的随机变量。根据3个站点降雨变化相关性的大小来初步选取Copula函数。为此，首先分析各个相邻站点间降雨量相关性大小。

由表2可知，上、中、下游3个站点的两两相关性较好，降雨相关系数最大达0.99，说明3个站降雨变化总体上存在较强正相关。

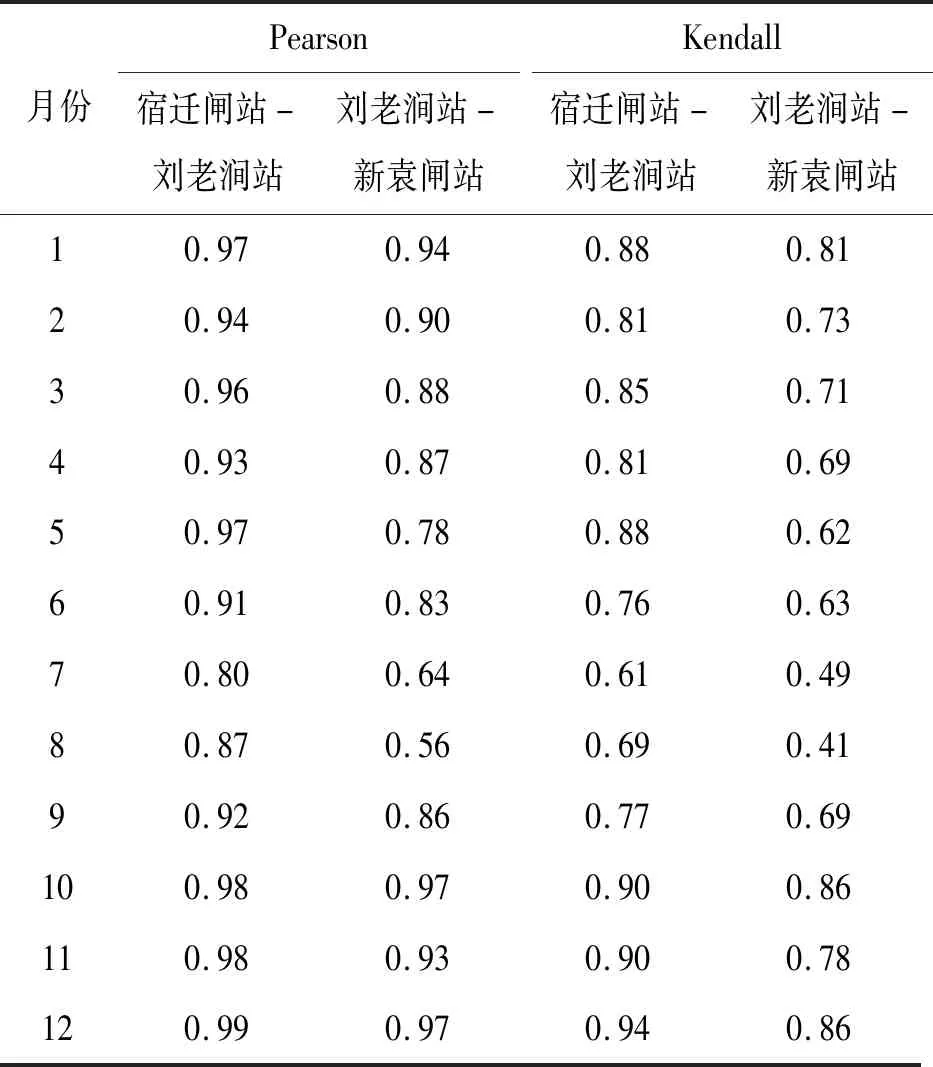
表2 相关系数计算结果

2.3 Copula函数参数估计及拟合优度检验

二维Copula函数的参数根据式(4)—(6)进行估计。为确定最优Copula函数，需对初选的3个Copula函数进行拟合优度检验。对3个站点不同时段降雨变化的观测值进行两两组合，(xi,yi)按x升序排列，得到新数据组(x1,y1)，(x2,y2)，…，(xn,yn)，二维经验联合概率计算公式为：

Fexp(xi,yi)=p(X≤xi,Y≤yi)=

(7)

式中Fexp——经验联合概率分布值；ng,k——所有满足X≤xi、Y≤yi的联合观测值的数目；n——序列长度。

其中5、9月降雨变化经验联合频率与理论联合频率的一致性检验见图2—5。从图可知，Clayton Copula、Frank Copula、Gumbel Copula 函数构造的理论频率和分布模型对经验联合频率的一致性较强，线性相关性在0.98以上。需要通过其他方法对Copula函数进行优选。

为选取最优Copula函数，采用AIC最小准则进行拟优选(表3)。通过分析，Gumbel Copula函数普遍优于Clayton Copula函数、Frank Copula函数。

a)Clayton Copula

a)Clayton Copula

a)Clayton Copula

a)Clayton Copula

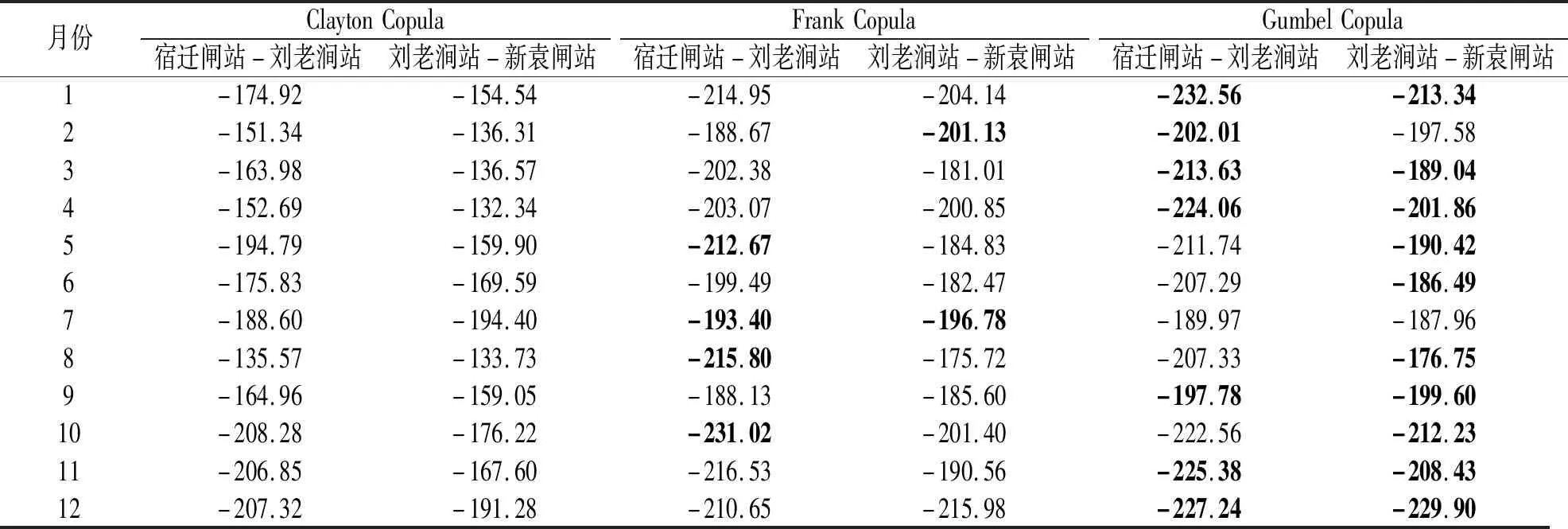
表3 AIC准则拟合优度检验结果

3 Copula函数随机模拟

随机模拟常采用的模拟方法主要有直接抽样法(一般适用于一维)、拒绝抽样法、重要性抽样法、MCMC抽样方法(分为Metropolis-Hasting算法与Gibbs采样算法)。

无论是拒绝抽样还是重要性采样，都是属于独立采样，即样本与样本之间是独立无关的，这样的采样效率比较低；MCMC方法是关联采样，即下一个样本与这个样本有关系，从而使得采样效率高。

Metropolis-Hasting算法的使用需要满足细致平衡的要求，而且这个算法有一个缺点，就是抽样的效率不高，有些样本会被舍弃掉，从而产生了Gibbs算法。Gibbs算法是用条件分布的抽样来替代全概率分布的抽样，而且舍弃的样本较少，效率较高，且能够较好地保留原有数据的属性特征。

Copula函数模拟月降雨量，采用条件概率的反函数，结合Gibbs抽样法对3个水文站的月降雨量进行随机模拟。根据选定的Copula函数，构造2个站之间的联合分布，利用Copula函数计算条件分布。

由表3结果可得，本次所选最优Copula函数中无Clayton Copula，故下文仅对Frank Copula、Gumbel Copula进行分析。根据式(1)—(3)可以得到Franke Copula和Gumbel Copula函数的条件分布函数，分别为：

F(v|u)=∂C(v,u)/∂u=e-uθ(e-vθ-1)/

[(e-vθ-1)(e-uθ-1)+e-θ-1]

(8)

F(v|u)=∂C(u,v)/∂u=

(9)

利用上述条件分布，结合Gibbs采样方法对月降雨量进行随机模拟。Gibbs采样方法的步骤如下。

步骤一生成随机数a0、a1∈(0,1);

步骤二令P(X1,1,1≤x1,1|X2,1,1=a0)=∂C(x1,1,1,x2,1，1)/∂x2,1,1=a1,其中Xi,j,k表示第k年j月i站的月降雨量，将其代入式(1)，求出v即为x1,1,1；

步骤三生成2个随机数a2、a3∈(0,1),求解方程组：

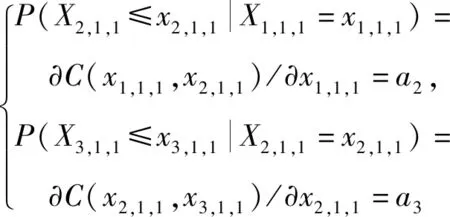
(10)

即得第1年第1月3个站点的月降雨量x1,1,1、x2,1,1、x3,1,1。

重复步骤三500次，可得500年的模拟月降雨量(图6、7，黑点表示实测值，灰点表示模拟值)。

a)宿迁闸站-刘老涧站

a)宿迁闸站-刘老涧站

4 结果分析

由图7可得，3站点间模拟值与实测值的走向基本一致，模拟点与实测点也较为集中，说明拟合值和实测值差别较小，拟合效果较好。

为进一步分析模拟值与实测值间的拟合效果，进行模拟值与实测值的均值、均方差、变差系数的误差分析，结果见表4。由表4可知，1月宿迁闸站与刘老涧站、3月刘老涧站、4月宿迁闸站的均方差、变差系数相对误差较高，经过分析可知，原数据存在降雨量极大值，导致边缘分布拟合误差较大。模拟值与实测值的均值、均方差、变差系数整体相对误差较小，基本处于10%以下，模拟效果较好。

表4 研究区模拟值与实测值误差分析

相邻站点间相关系数的误差分析结果见表5。

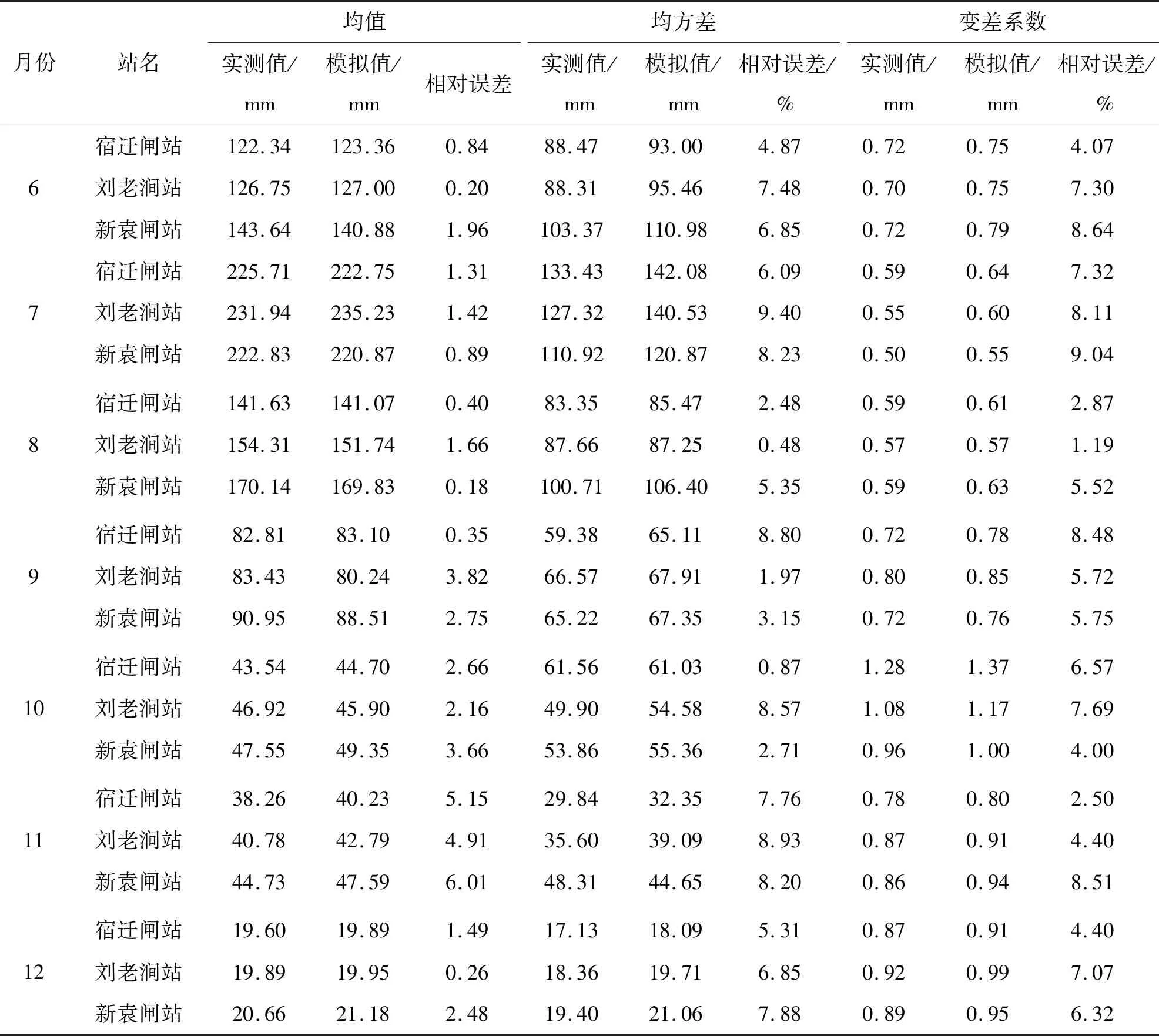
续表4 研究区模拟值与实测值误差分析

表5 研究区相邻站点间相关系数模拟值与实测值的误差

续表5 研究区相邻站点间相关系数模拟值与实测值的误差

由表5可知，各站点间Kendall相关系数、Spearman相关系数相对误差均较小，最大为8.93%。说明本次模拟基本保留了原有观测值的统计特征。

5 结论

本文通过Copula函数法对上游宿迁闸站、中游刘老涧站、下游新袁闸站3站的月降雨量进行了随机模拟，结果表明，该3站月降雨量存在较强的正相关性，二维Copula函数结合Gibbs采样法可有效建立同流域相邻站点间的相关性结构，模拟结果能够较好地保留原有观测值的统计特征。该法简单易懂，可为其他水文要素的随机模拟与中长期概率水文预报提供参考。