最小均方电液负载模拟器加载系统控制研究
2021-04-20李建英谢寅凯
李建英,谢寅凯,谢 帅
(哈尔滨理工大学机械动力工程学院,黑龙江 哈尔滨 150080)
0 引 言
电液伺服系统的主要优势特点是响应速度快、功率-体积比大、抗负载刚度大等[1]。电液负载模拟器是电液伺服系统的一项重要应用,因其上述绝对优势,主要被用在测试飞行器或船舶等在行进的过程中,其受载荷舵面在受到各种载荷谱作用下的响应性能[2-4]。为了使动态模拟性能能够达到被加载对象在实际应用使用时的真实效果,加载系统的性能指标中必须要有精确性、及快速地复现各种对应载荷谱的要求,从而具有良好的动态加载性能。由于电液负载模拟器的加载系统在动态加载的工况下,还受到被加载系统(舵机系统)按照实际需要运动时,在活塞杆之间刚性连接情况下,对加载系统施加的强干扰,就会在加载系统中产生强迫流量,由于流量和压力之间的非线性关系,进而在加载系统的执行机构中形成多余力[5-7]。当多余力和实际需要的精确加载力交融后作为加载系统总和输出力的时候,力加载精度就会被严重降低,甚至可以达到所需精确加载力的若干倍,严重影响了电液负载模拟器的动态加载性能,而且动态运动频率越高,力加载精度越差,呈恶化趋势[8]。目前,削弱多余力以提高力的动态加载性能依然是研究的热点问题,解决这一难题的措施主要有硬件结构改型和采用合适的控制策略或对策略算法规则进一步改进以达到新的实际控制效果两个主要方向[9-10],也取得了相应的进展,达到了较好的应用效果。但是,在系统动态加载频率要求进一步提高、对系统的快速性有更高要求的时候,动态加载力的误差仍然比较大的矛盾依然会显现出来,主要表现在由于多余力的存在而使加载输出力的幅值比理论输出值大、相位也会比输入信号的相位超前严重。
为了解决在不断提高加载频率的快速性指标需求情况下,动态力加载精度性能反而不高的实际现状,本文提出了基于最小均方算法的神经网络控制策略应用于电液负载模拟器加载系统。为加载系统设计新的控制器,将其设置在输入信号和加载系统之间,其工作原理是:将设定信号经过相应权值运算后的输出量与加载系统输出信号经过相应权值运算后的输出量做差,得到的二者之间的差值,即为整个神经网络控制输出的误差,再将该误差作为权值自身调整算法的输入,就可以通过反复在线实时调整各个相应权值,从而实现输出力与设定信号之间的差值逐渐缩小的目的,使得二者趋于同步。
1 电液负载模拟器的数学模型
电液负载模拟器的等效图如图1所示,线性化后的加载系统电液伺服阀的流量连续性方程为[11]:
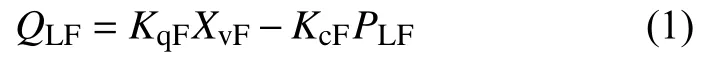
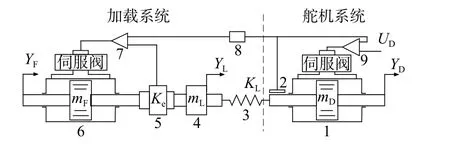
图1 电液负载模拟器等效图
式中:QLF——加载系统电液伺服阀的负载流量,
KqF——加载系统电液伺服阀的流量增益;
XvF——加载系统电液伺服阀阀芯的开口量;
KcF——加载系统电液伺服阀的流量—压力系数;
PLF——加载系统加载液压缸的负载压力。
加载系统加载液压缸的流量连续性方程如下式所示:
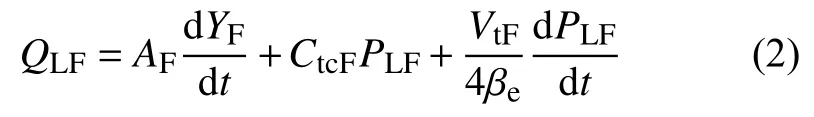
式中:AF——加载系统液压缸活塞的有效面积;
YF——加载液压缸活塞移动的位移;
CtcF——加载液压缸总的泄漏系数;
VtF——加载液压缸两个容腔的总容积。
如果忽略库仑摩擦作用和液压油油液质量,根据牛顿第二定律,可以得到加载系统加载液压缸的力平衡方程如下式所示:
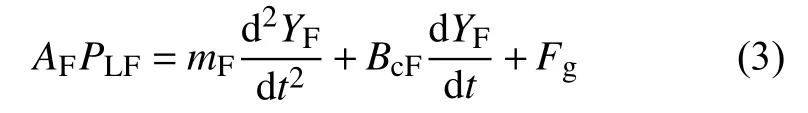
式中:mF——加载液压缸活塞和活塞杆所组成的组合件的质量;
BcF——加载液压缸的粘性阻尼系数。
同时,电液负载模拟器系统检测力传感器的输出力如下式所示:

其中Ke为检测力传感器的等效刚度。
由于在检测测量环节,本项研究采用了大刚度的检测力传感装置(器),从而可以大贴合率的近似实现YL=YF的实际效果,就可以在物理实际角度认为加载系统检测力传感器的输出力即为加载液压缸活塞杆的输出驱动力,那么加载系统检测力传感器输出力的传递函数可通过下式来求得:

分析式(5)中的特征参数可知:加载系统中使用的液压动力机构当中的一阶惯性环节的转折频率是,同时,其中的二阶振荡环节的转折频率是以及二阶振荡环节的阻尼比。通过这些即可进一步求解分析加载系统的特性。
由于功率放大器和检测力传感器二者各自响应频率都要比机械和液压环节本身的频率高得多,所以直接利用二者各自的简化传递函数形式即可,再联合电液伺服阀作为二阶振荡环节考虑时的传递函数和上述分析,就可以得到加载系统的开环传递函数,如下式所示:

2 最小均方算法神经网络控制策略
论文中所采用的神经网络控制策略的性能指标是均方误差,该控制策略在结构上,主要是由自适应线性神经元网络和最小均方算法的学习规则组成的。在最小均方算法的规则中,主要工作是通过算法改进之后,可以加快求解计算过程中的随机梯度,进而经过逐次迭代不断优化的方式,可以达到更高效调整自适应线性神经元网络里的权值向量的目的。同时,重点是该迭代调整,可以在相对于被动态调整权值的误差平方幅度的变化梯度的方向上来完成,所以其优势就在于在上述过程中,并不需要像原先那样做相关复杂又比较耗时的矩阵求解或矩阵逆运算[12],使得其具有相对简单的结构、同时还具有高效的运算过程等特点,从而使其能够在比较多的、不同的运行工况条件下,所展现出来的权值调整、运行效率、精度等综合性能都比较优良,实际应用效果明显。将这些优势和特点应用在电液负载模拟器的加载系统控制策略设计上,就可以针对性解决加载系统在强干扰作用下、加载工况变化情况复杂时导致加载性能差的问题。
在神经网络控制策略中,自适应线性神经元网络所输出向量的第i行元素如下式所示:
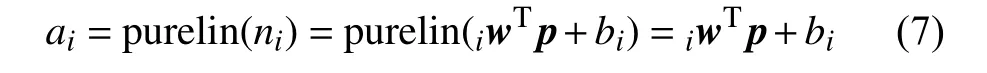
其中iwT为权值矩阵w的第i行元素,即下式所示:
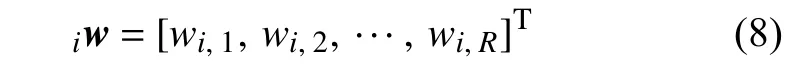
当需要通过上述结构来构造一个神经网络线性控制器时,可以采用的输入信号向量如下式所示:
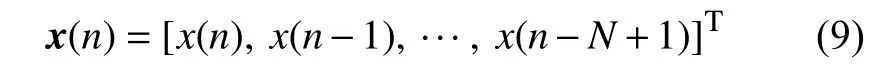
其中该神经网络的权向量就可以由下式表示为:
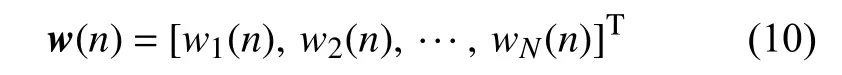
则所设计的神经网络线性控制器在n时刻的输出可由下式表示为:
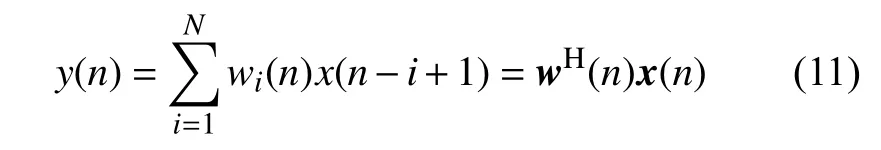
假设:d(n)为神经网络线性控制器的期望响应输出值,则该控制器的误差e(n)可以用下式得到:
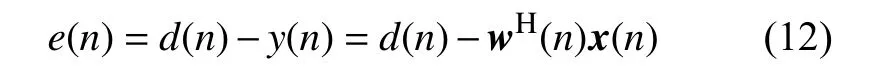
由式(7)~(12),结合上述分析过程,可以得到自适应线性神经元网络控制器,其原理图如图2所示。
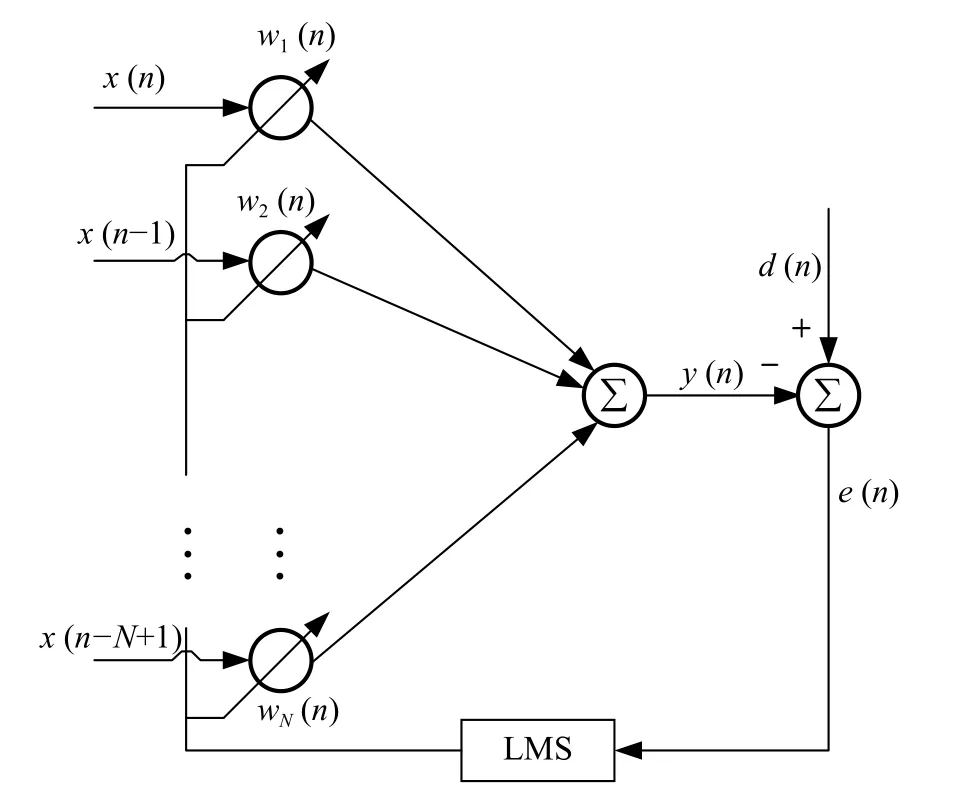
图2 自适应线性神经网络控制器原理图
3 基于最小均方算法的加载系统神经网络控制器的设计
电液负载模拟器在结构上尤其是联接结构上是具有强相互耦合特点的较为复杂的机-电-液一体化程度高的复合系统[13]。模拟器里面的加载系统在对被加载对象动态加载的过程中,出现了不必要的多余力作为干扰力存在,对加载力的加载精度造成了很大的影响[14],而且通过分析得知多余力的表现,尤其是在正弦信号输入下的特性,是输出相位的超前和幅值的增大,甚至于在某些特殊工作的工况下,多余力比所需要的正常加载力高出很多甚至若干倍;在动态加载而且加载频率比较高的工况下,更是特别严重[15]。为此,本论文在研究中,为电液负载模拟器的加载系统设计了一个基于最小均方算法的自适应线性神经网络控制器,来提高加载系统在上述分析的干扰工况工作状态下的动态综合加载精度。
按照上一节的分析结果,结合加载系统的特点,我们可以把加载系统的输入信号做数学变化后如下式所示:
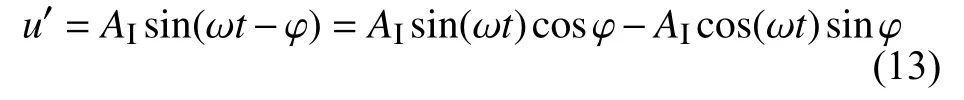
接着再分别用权值w1和w2代替公式(13)中的余弦值和正弦值,则公式(13)变化后可表示为下式:
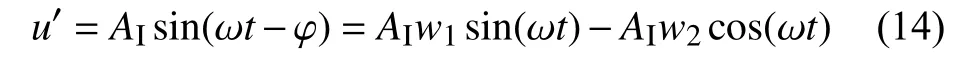
在此分析的基础上,对于电液负载模拟器的加载系统而言,所设计的自适应线性神经网络控制器的原理图如图3所示,则该控制器的输入信号有两个,分别为预先设定好的输入信号u和另外一个输入信号u′′,将两个输入值u和u′′分别与图中各自相对应的加权值w1和w2相乘,再按照图中所示算法规则进行运算之后,就可以得到综合输入信号。然后,再将综合输入信号作为加载系统的输入信号。对于运算过程中的 φ值而言,应用自适应线性神经网络而实现的u和u′′及其各自权值w1和w2之间的关系,并利用最小均方算法可以在线调整后得到算法运算所需要的加权值。接着再将整个自适应神经网络策略的输出误差e作为最小均方算法的输入值;这样,应用该算法循环计算、并反复多次在线实时变化调整两个加权值,由前述分析的、所设计的该算法规则运行原理可以得知,最终就可以用第n次循环迭代时的误差平方值e2(n)来代替原有的均方误差值,从而我们得到了所述自适应线性神经网络的权值变化的算法为:
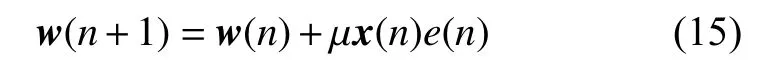
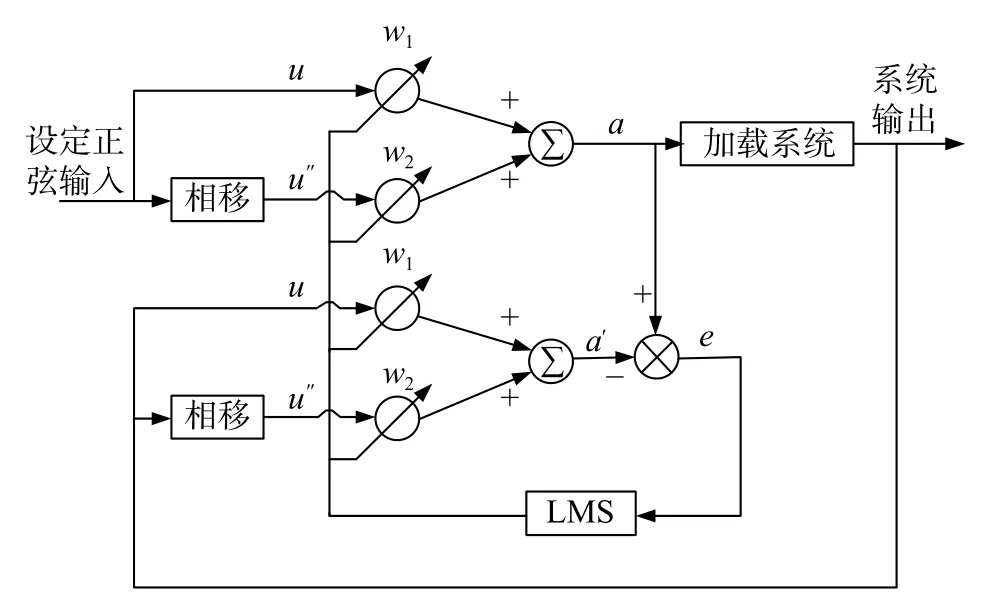
图3 最小均方算法的神经网络控制器原理图
这样,就在输入信号和加载系统之间设计增加了一个基于新算法规则的最小均方算法自适应线性神经网络控制器。
4 加载系统的仿真分析
下面对基于最小均方算法所设计的自适应线性神经网络控制器来控制的电液负载模拟器加载系统动态力加载进行仿真分析,仿真结果曲线如图4所示。其中,图4(a)是没有采用本论文中所设计的神经网络控制器时加载系统的加载输出力响应曲线,而图4(b)是应用了基于最小均方算法设计的自适应线性神经网络控制器之后的加载系统的加载输出力响应曲线,如图中所示,曲线1是所设定的输入信号曲线,曲线2则是加载系统加载输出力信号曲线。从图中可以发现,在没有应用神经网络控制器时,加载系统在运行之后,其输出可以对设定的输入信号实施随动跟踪,但是调整结束并且稳定工作之后,加载误差依然存在,而且相对来说还是比较大的;并且,明显出现了输出信号的幅值增大,相位超前的现象。在对加载系统应用了基于最小均方算法所设计的自适应线性神经网络控制器之后,加载系统在初始阶段也要经过一定周期的调整,并且可以看出调整的幅度或者说此时调整所出现的误差比较大、调整过程显得比未加控制器时的情况要剧烈一些,但其输出也还是能对设定输入信号进行跟随复现的。不过,明显看出整个调整的时间周期变短了,而且,当自适应调整结束以后,输出信号和设定输入信号之间的稳态误差值明显减小,二者趋于一致,从仿真结果来看,说明基于最小均方算法所设计的自适应线性神经网络控制器可以有效地改善加载系统的动态力加载的动态响应特性。
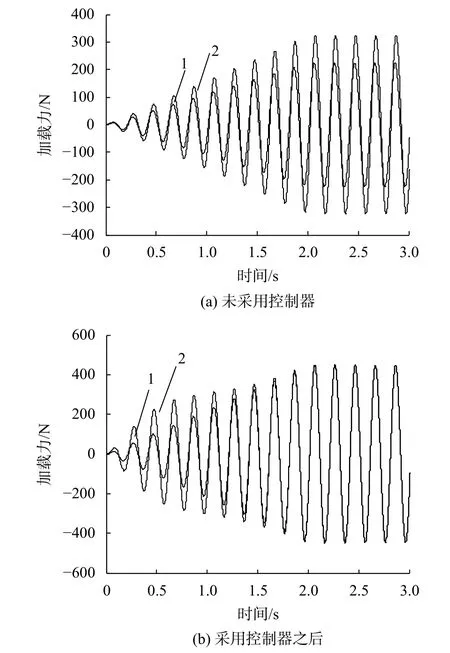
图4 最小均方神经网络控制下系统仿真响应
如图5所示,在给定输入信号的频率为5 Hz时的正弦信号作用下,加载系统动态加载力输出的响应仿真曲线,其中,图5(a)是没加本文所设计的控制器情况下系统的输出仿真曲线,图5(b)是采用了基于最小均方算法所设计的自适应线性神经网络控制器之后系统的加载力输出仿真曲线。图5(a)和图5(b)中的曲线1均为输入信号曲线,曲线2均为加载系统的加载力输出曲线。通过分析仿真结果可以看出,图5(a)所显示的加载系统的加载输出精度是比较低的,其中明显的具有相位超前和幅值增大的现象,而从图5(b)显示的仿真结果来看,调整的初始阶段输出信号的幅值增加的特别剧烈,加载系统的输出响应性能比较差,力加载输出曲线的幅值甚至比预设输入信号的幅值高出1倍,相位也有明显的超前。随着自适应线性神经网络控制策略调整的持续进行,力加载输出曲线逐渐向输入信号靠近,加载系统的响应性能明显好转并可以有效保持住。

图5 加载系统动态力加载时系统响应曲线
5 基于最小均方算法自适应线性神经网络控制加载系统的实验研究
在电液负载模拟器的加载系统采用了基于最小均方方法所设计的自适应线性神经网络控制器之后,对其动态力加载性能进行实验研究,实验分别进行了采用神经网络控制器之前与之后的加载系统动态力加载的性能对比研究,实验曲线如图6所示,图中曲线1是给定的输入信号曲线,曲线2是加载系统动态加载输出力信号曲线。
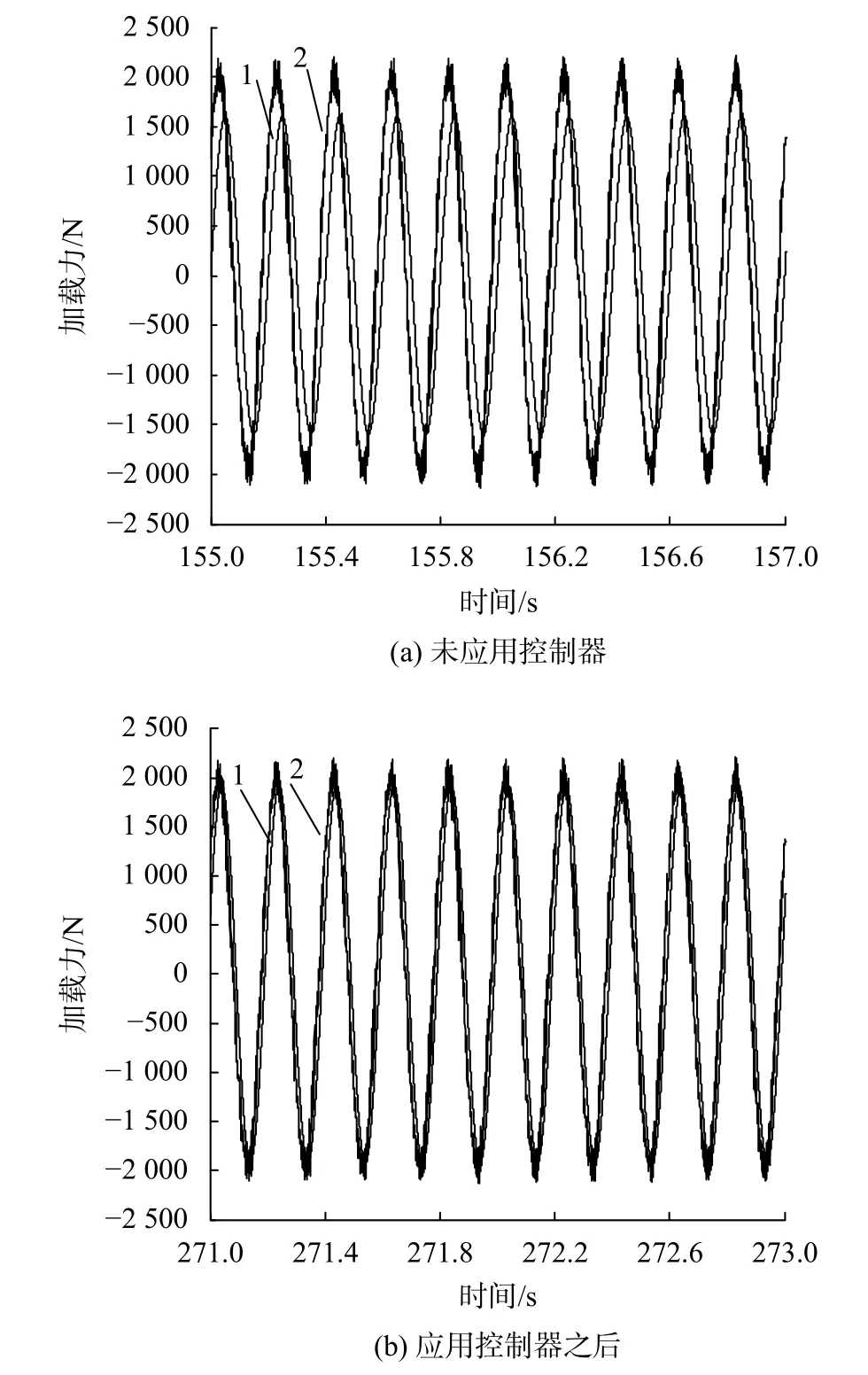
图6 应用最小均方神经网络控制器前后动态力加载实验曲线
从图6中可以看出,当加载系统进行动态力加载的时候,其力输出在经过初始状态较短时间的调整之后,就能够较好地随动跟踪上设定的输入信号,有效减弱了曲线中的幅值超高和相位超前的动态运行误差。
其中,图6(a)是没有应用所设计的控制器进行控制情况下电液负载模拟器加载系统的动态力加载实验曲线,图6(b)是采用了基于最小均方算法所设计的自适应线性神经网络控制器控制加载系统时的动态力加载实验曲线,通过对比实验曲线可以看出,图6(a)中所显示出来的幅值增大和相位超前问题,在图6(b)中得到了很好的解决,加载输出力曲线很好地复现了设定输入信号曲线,说明基于最小均方算法的自适应线性神经网络控制器有效地改善了加载系统动态力加载时的加载精度和具有较高加载频率运行工况下的综合动态响应特性。
6 结束语
本论文所研究的基于最小均方算法自适应线性神经网络以及在此方法下所设计的控制器,主要是针对电液负载模拟器加载系统动态力加载时出现的加载精度低,动态加载快速性不高的问题。设计控制器的主要工作是通过算法改进之后,自适应线性神经元网络单元和最小均方学习规则可以实现更高效地调整神经元网络里的权值向量这一核心要素的目的。仿真和实验结果表明:在应用文中所设计的控制器之后,加载系统的动态加载力输出响应曲线能很好地随动跟踪所设定的输入信号,并在较短初始调整阶段结束以后能够和设定输入信号的幅值与相位趋于一致,实验中较好地解决了输出幅值超大、相位超前的实际问题,从而达到实现较为精确动态加载输出力的目的。用该方法设计的控制器在工作过程中循环迭代时运算效率高,具有较强的实时性,综合效果较好。
