数据驱动工业异常值检测与容错模型研究
2021-04-20张超凡张凯文
钱 虹,张超凡,张凯文
(1. 上海电力大学,上海 200090; 2. 上海市电站自动化技术重点实验室,上海 200090)
0 引 言
随着工业自动化水平不断提高,对工业过程控制数据的准确性和可靠性的要求也越来越高。工业过程数据在采集、传输、储存过程中极易受工业噪声、传感器故障、I/O口接触不良、恶意网络假数据注入攻击等因素干扰使得过程数据异常,控制系统难以实现闭环稳定运行[1]。因此,实时对工业过程控制数据进行异常检测并对异常数据进行高精度恢复,实现系统可靠容错运行,对整个工业生产过程安全、高效的工作是十分必要的[2]。
在工业控制现场,若输入分布式集散控制系统(distributed control system,DCS)控制器的信号受外界因素干扰发生数据异常,并将异常数据代入后续的模型、控制量计算中,必将影响控制系统的性能,甚至导致整个控制系统崩溃。因此,实现对工业过程数据的异常检测并对异常数据进行高精度恢复,维持系统短时容错运行,是当下对整个工业系统安全可靠运行研究的热点之一[3]。传统硬件冗余法,虽然可以提高采集数据的可靠性和准确性,但其以高昂成本和系统复杂度的增加为代价。基于数据驱动的软测量方法,在充分利用历史数据的基础上,可以对目标变量实现较高精度的观测。对输入DCS中的测量数据和软测量结果进行残差分析,可实现对实际测量数据状态的检测[4]。在目前的研究与应用中,当检测到工业过程控制数据异常时,为维持系统短时容错运行,常以异常前数据尾值、样条插值、滑动平均值、软测量模型的预测值替代异常数据值进行异常数据恢复,但数据恢复精度往往不能达到令人满意的效果。
文献[5-6]利用主元分析的方法对工业过程数据进行异常检测,并利用数值计算中的插值方法进行异常点数据恢复,但忽略了输入输出之间的非线性关系,使得对异常数据的恢复精度不高。文献[7-10]使用支持向量机(support vector machine,SVM)、神经网络等智能方法建立软测量模型对工业过程数据进行检测,并用预测值替代异常数据,此类方法对数据的恢复精度取决于使用的软测量模型的精度,而精度较高的软测量模型往往结构复杂、计算量大,难以实现对过程数据的实时检测。文献[11]基于距离加权最近邻(K-nearest neighbor,KNN)回归算法对交通流异常数据进行恢复,但在验证过程中没有考虑到每个输入特征对回归值的影响不同,回归精度有待提高。岭回归(Ridge regression,RR) 是一种以结构风险最小化为学习规则的算法,与神经网络相比具有更高的泛化性能,特别是在样本有限的情况下,效果更为明显。文献[12-13]分别将岭回归应用于内模控制和房价预测,其结果表明,岭回归的应用使得实验结果均有所改善。
为了保证在传入DCS控制器中的数据出现异常时工业控制系统仍能维持短时容错稳定闭环运行,为运行人员采取应急响应措施赢得时间。本文提出基于KNN和Ridge回归算法相结合对工业过程异常数据实现高精度恢复,并在此基础上构建控制系统自切换容错运行模型。在应用某电厂实际运行数据构建对SCR出口NOx排放软测量模型的基础上,对所提模型进行验证及与其他数据恢复方法对比效果。结果表明,基于KNN和Ridge回归算法对异常数据的恢复方法具有较高的恢复精度,能够可靠地应用在工业容错控制运行过程中,提高整个系统的安全性和稳定性。
1 异常检测与容错模型构建
本文构建的工业过程控制异常数据检测与容错运行模型,其整体原理框架结构如图1所示。首先对控制系统的被调量,即输出变量y构建基于径向基核函数的支持向量回归机(radial basis functionsupport vector regression,RBF-SVR)数据驱动软测量模型,根据实时工况数据计算出预测值,然后将输入异常值检测模块并结合实时测量值yi实时计算数据的准确度A,以此判断实时测量的数据是否异常。当检测到数据异常时,发出使能信号激活异常数据恢复功能,通过KNN算法从历史运行数据库中搜寻与异常数据输入特征最近邻的K个工况点并利用Ridge算法对这K个近邻点进行回归运算,实现对异常数据高精度的恢复。最后通过容错切换机制实现工业控制系统发生数据异常时将Ridge回归值替代异常数据,从而实现控制系统短时稳定容错运行。

图1 容错运行原理框架结构图
1.1 基于RBF-SVR软测量模型
复杂工业过程控制中的部分关键工艺参数难以实现连续在线检测,使得常规闭环控制系统难以实现。软测量模型基于对大量历史运行数据的训练,具有一定的测量精度,既可应用于对许多难以连续测量的热工过程参数进行监测,也可用于异常数据诊断[14-15]。考虑到实际工业现场计算机其配置和运行环境偏差的原因,如果使用需要较高算力的基于神经网络等软测量方法,虽然可以在测量精度上有所提高,但需要更换更高配置的计算机,经济性变差,而且由于其复杂建模过程带来的运行时间变长,也会使得模型实时性变差。支持向量机SVM遵循VC维理论,是结构风险最小化原则的应用,其具有小样本、高维性、泛化能力强等优点,常用于建立软测量模型[16-18]。
在相同硬件环境下分别使用线性回归(linear regression,LR)、基于线性核函数的支持向量回归机(linear-support vector regression,L-SVR)、基于径向基核函数的支持向量回归机(RBF-SVR)、随机森林(randomforestregressor,RF)、深度神经网络(deep neural networks,DNN)对经典波士顿房价数据集[16]进行建模回归。为避免偶然性对结果产生影响,对各模型运行20次后计算均值。其模型构建时间、计算机内存占用、预测数据的均方根误差 (root mean square error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)对比如表1所示。
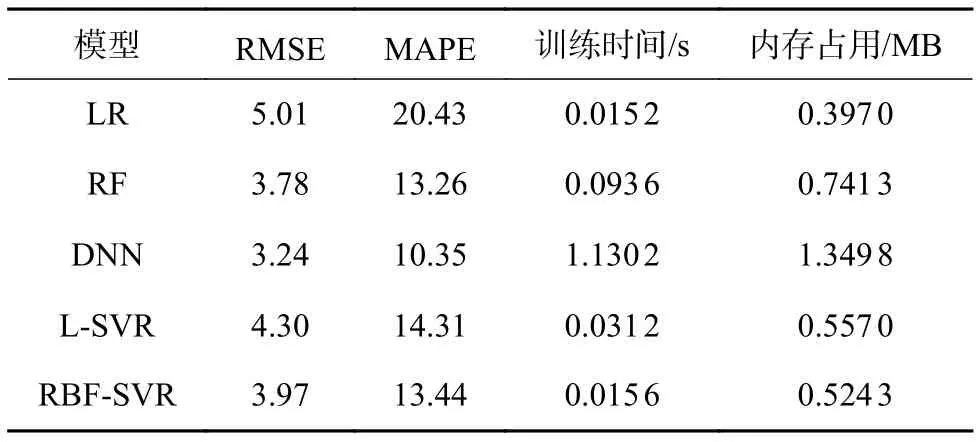
表1 算法性能对比
由表1数据分析可知,基于支持向量机的软测量方法与其他模型在训练精度和预测精度相差极小情况下,训练模型占用计算机的内存小、运行时间少[17-19]。在样本数目较多、维数较高时采用径向基核函数建立的支持向量回归相比其他核函数模型具有更高的模型辨识度[20]。综上本文软测量采用RBFSVR模型。
对于训练集T={(x1,y1),···,(xi,yi),···,(xl,yl)},其中xi∈Rm为实例的特征向量,yi为1维目标变量实际测量值,l为样本个数。构建回归函数:

式中:w——权重;
b——阈值;
则SVR模型可表示为求解如下最优化问题:
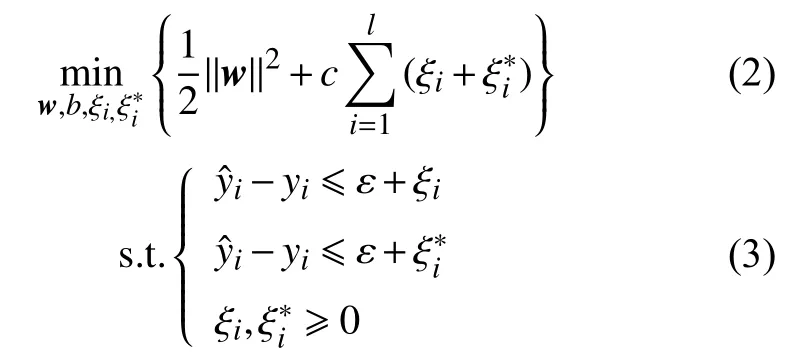
式中:c——惩罚因子,本文取c=1;
ε——不敏感系数。
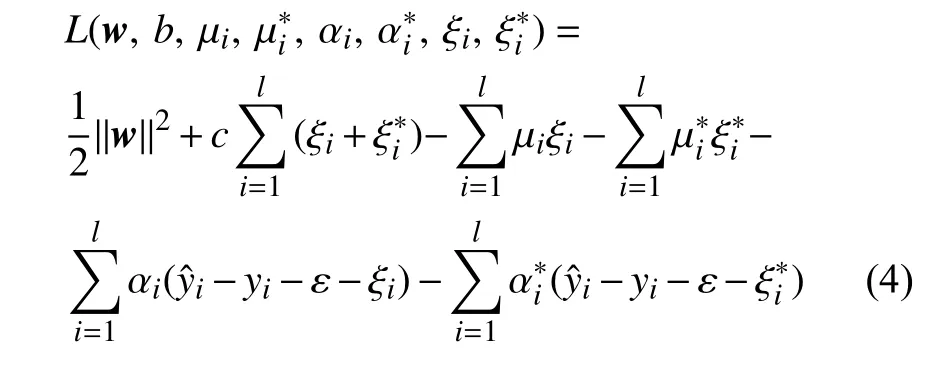
再令L对求偏导为零可得:
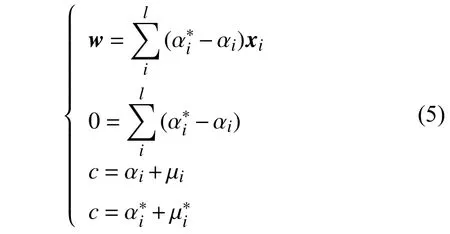
借助KKT条件求解出式(5)并带入式(1)可得SVR模型预测值:
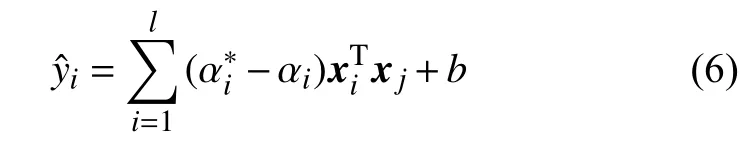
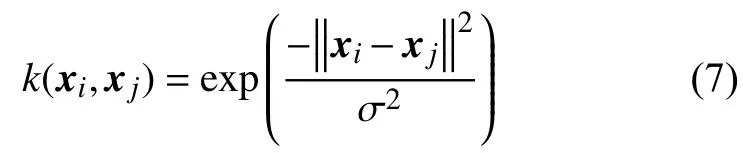
1.2 异常值检测
为了判定工业过程数据是否异常,本文定义数据 (xi,yi)的准确度为:

系统正常运行时软测量模型预测值和目标变量测量值的偏差在一定的范围内,故其准确度也在固定范围变化,即:

其中d为准确度阈值,可基于历史运行数据利用统计学方法获得。当检测设备故障或由其他原因导致测量数据值出现异常时,数据准确度Ai将小于阈值d,异常值检测模块判定该实际运行点数据为异常数据点,此时所得的测量数据值已不能正确表示系统实际运行状态。若控制系统在依此异常数据基础上进行控制操作,必将使系统失去正常的运行条件,引起系统运行崩溃,甚至引发人员误操作,酿成事故。
1.3 异常数据的KNN分类
出现异常数据 (xi,yi)时常以软测量预测值代替异常数据值yi,但该方法的准确性受到软测量模型的限制,往往不能有效的用于系统容错运行中。为了提高故障点数据恢复精度,本文首先利用KNN分类器在历史运行数据库中将异常数据点对应的特征向量xi最近邻的K个实例点选出组成数据集Nk,即:

其中 (xiK,yiK)表示异常数据点 (xi,yi)的第K个最近邻点。这K个近邻点和异常数据点的运行工况最为接近,其变量特征xik和 异常实例点变量特征xi在同一划分范围内,具有很强的相似性。然后对这K个点的输出变量值进行加权平均操作得到修正后的预测值。具体步骤如下:
1) 根据给定的距离度量计算训练集T中实例点 (xj,yj)与异常数据点 (xi,yi)的距离。其中距离一般为Lp距 离,即:
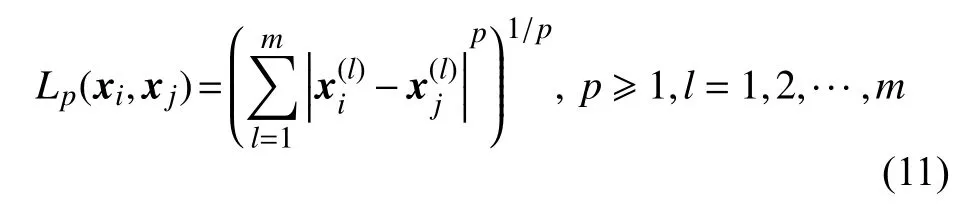
2) 将距离排序,选取距离最小的K个最近邻实例点,并将涵盖这K个点的邻域记做Nk(xi)。
3) 在Nk(xi)中根据距离xi的远近对K个实例点对应的输出变量y={yt},t=1,2,···,K进行加权平均,得到xj的目标输出变量值。即:

其中目标输出变量yt对应的权重wt为:
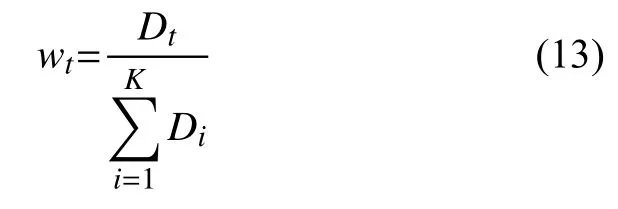
1.4 基于Ridge算法提升数据恢复精度
KNN算法具有理论简单、精度高的优点,如果仅根据K个最近邻点对应的输出变量进行距离加权平均得到回归值,其忽略了实例样本点特征向量xi中每个特征对目标变量回归值的影响不同,其数据恢复精度可进一步提高。
线性回归模型利用最小二乘法求解每个特征对应的最佳权值,以使得损失函数最小。其权值的大小反映了对应特征在预测中的重要性,但如果实例样本点的个数K小于样本点的维度m时,线性回归模型将出现多解,且模型存在过拟合现象。Ridge回归算法是基于线性回归模型基础上加入L2正则化项所得到的更加稳健的回归算法,其把模型的解空间限制在一定的范围内,来防止过拟合现象。故本文在KNN的基础上对所选出的K个近邻点使用带L2正则项的多元线性Ridge回归器进行数据拟合,使得其在输入实例样本点很少的情况下,也可以获得较高的回归精度。
对经KNN算法选出的K个近邻值组成的数据集Nk(xi)其线性回归模型为:
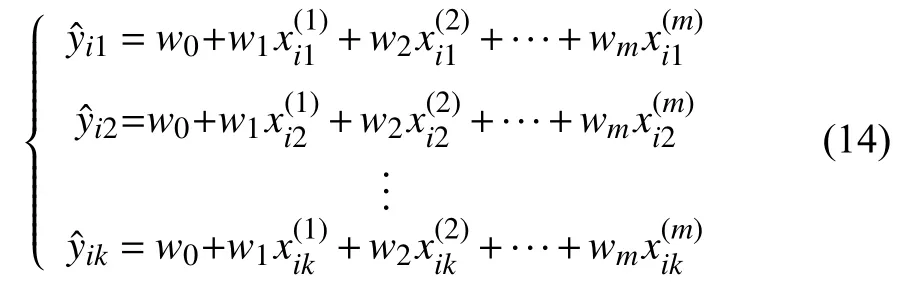

为了确定最佳的权重系数w∗,引进损失函数:

其中yij为Nk(xi)中第j个数据点的目标变量测量值。对上式进行最小二乘参数估计可得线性回归可求得Ll(w)最小时的参数w∗。
由于Ridge回归中加入L2正则化项,故Ridge回归算法的损失函数为:
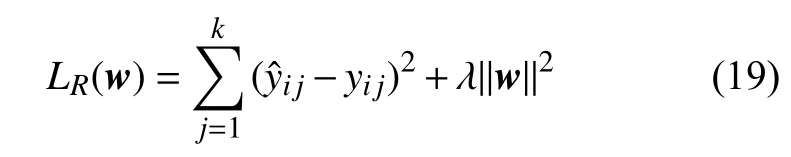
其中 λ为正则化系数,可以通过岭迹法、网格法等方法求出。LR(w)的第一项表示对训练实例点的拟合程度,与第二项正则项相结合来防止模型过拟合。且有:
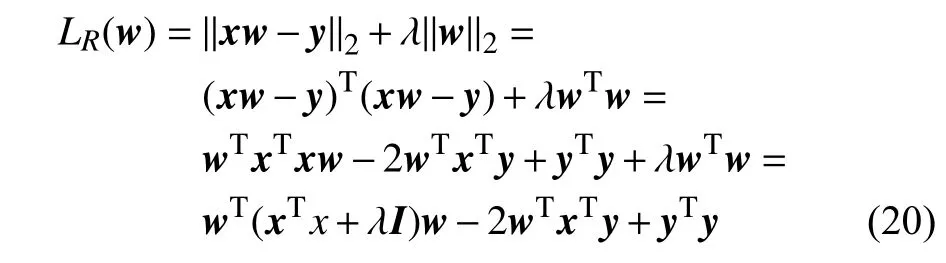
其中I∈R(m+1)×(m+1)为单位矩阵。为了求最佳权重系数使得LR(w)最小,即:
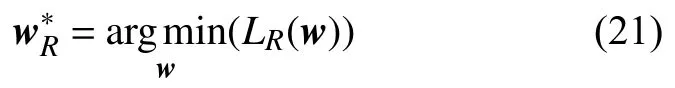
常用的做法为对目标函数关于w求偏导数,一阶偏导数为0时所对应的w即为最佳系数。 即:
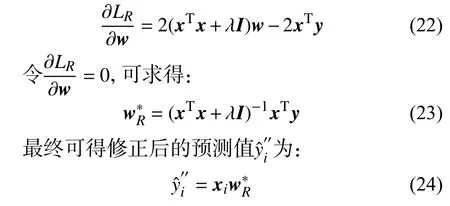
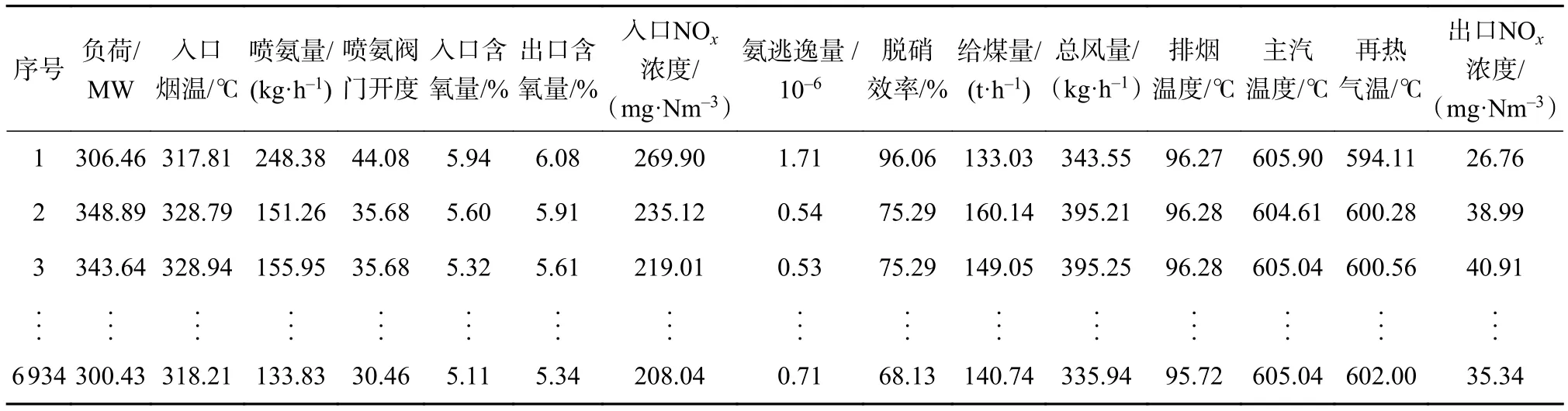
加入L2正则化项,既可以保证当K 为了使控制系统在过程数据处于正常或异常状态下都能闭环稳定运行,设置容错切换模块实现自切换功能。当测量数据值经过异常值检测模块计算其数据准确度在d≤Ai≤1范围内时,表明实时测量数据正常,此时该模块输出y为实际测量值yi。否则,判断测量数据为异常数据,输出值y为经Ridge回归修正后的预测值。即: 本文以某电厂650 MW煤锅炉SCR脱硝系统出口NOx浓度为目标输出变量,从电厂分布式控制系统DCS中采集为期10日,采样时间间隔为1 min,利用 3σ 准则去除异常无效值后最终获得包含265 MW、270 MW、300 MW、310 MW、330 MW、360 MW、390 MW、395 MW、401 MW、410 MW、420 MW、500 MW、600 MW共13种稳态运行工况的共6 934组数据。其中每条数据样本包含负荷、喷氨量、总风量等14个反映SCR脱硝过程的特征变量及脱硝出口NOx浓度输出变量,其中部分数据展示如表2所示。 表2 部分仿真数据展示 由于SCR脱硝系统反应复杂多变,涉及诸多过程变量,且输入变量之间存在多重共线性,不但使得建模过程变慢,而且影响软测量模型的预测精度。因此剔除噪音变量,得到最优输入变量集是建立快速、准确的数据软测量模型的前提。本文通过公因子与主成分分析法进行变量提取。从图2公因子分析特征值变化图可以看出,前3个变量的信息量明显较高,第9~14个变量并未出现明显的断层,信息量呈持续下降趋势。进一步对各变量进行主成分分析,计算结果如表3所示。可以看出,前7个变量的累计方差贡献为94.375%。 图2 公因子分析特征值变化图 表3 各主成分对应的特征值及其方差贡献率 根据特征值与方差贡献率的大小,最终选择前7个变量作为NOx排放浓度SVR软测量模型的输入变量。那么i时刻模型对应输入特征向量xi与目标输出变量yi为: 式中:pi——负荷; Ni与ni——脱硝系统入口、出口NOx浓度; ki——喷氨阀门开度; vi——喷氨量; Ti——入口烟温; Hi、hi——脱硝系统入口、出口含氧量。 最终建立SCR脱硝出口NOx排放的EBF-SVR软测量模型,如图3所示。 图3 RBF-SVR软测量模型 本文在Windows系统平台上借助编程软件python实现本文所提的方法并进行结果展示。主体部分编写两个类函数,第一个类函数用于建立基于RBF-SVR对SCR出口NOx排放软测量模型。第二个类函数用于实现异常数据的恢复和输出切换。验证程序的整体编程流程图如图4所示。 图4 验证程序流程图 2.2.1 RBF-SVR软测量模型 从6 934组数据中随机选取6 240组数据作为基于RBF-SVR的NOx排放软测量模型训练样本,剩下694组数据作为测试样本。在RBF-SVR模型中径向基函数的超参数 σ选取的好坏影响软测量模型的预测精度和泛化能力,不同的数据集具有不同的最佳 σ。为了使建立的模型具有最佳的预测性能,采用带有交叉验证的网格搜索法(grid search with cross verification),以测试集数据的r2得分为指标,对超参数 σ进行寻优,得到如下图5所示关于模型预测准确性和 σ学习曲线。最终确定对于本文使用的数据集最佳超参数 σ的值为14.21。 图5 模型预测准确性和σ 关系曲线 应用RBF-SVR软测量模型对SCR出口NOx排放计算效果如下图6所示。从图6中(a)、(b)中可以看出训练值与测试值均紧密分布在理想直线上下,具有较小的方差和偏差,图(d)中预测偏差也均匀分布在0值左右,表明所建立的软测量模型能够准确、可靠的反映 SCR 系统的反应特性和动态变化过程。将预测值与实际测量值带入准确度计算公式(8)可得测试集数据的准确度,最终结果如图7所示,可知当数据正常时,实际测量数据的准确度在[0.8,1]的范围内变化,阈值d=0.8。 图6 RBF-SVR软测量模型训练及预测效果图 图7 测试集数据的准确度 采用均方根误差 RMSE、平均绝对百分比误差MAPE和决定系数 作为模型评价指标。为避免偶然性影响预测结果,对所建立的出口NOx排放软测量模型进行训练与测试 20 次后取均值,最终得到模型性能如表4所示。 表4 RBF-SVR模型评价 从表4中数据可知,基于RBF-SVR的NOx排放软测量模型,无论是对训练样本的拟合还是对测试样本的预测,所建立的软测量模型都具有较高的精度,拟合和泛化能力较强,能够实现对目标变量即SCR出口NOx浓度的较高精度的测量,从而可以为判断传入DCS中的实际测量值是否异常提供参考依据。 2.2.2 基于KNN和Ridge回归算法数据恢复方法验证 为了更好验证本文提出算法有效性,将测试数据中序号为490~498共9个点设为受外界干扰后出现的模拟异常数据点,设目标变量的异常数据值为[0,5]之间的随机数。 应用RBF-SVR模型对出口NOx排放进行软测量以实现对目标变量的数据状态进行观测。如图8所示,当外界因素使得测量数据发生异常,其测得数据的准确度将越过正常数据的准确度区间[0.8,1],这说明异常值检测模块能够准确检测出异常数据,为之后异常数据恢复以及容错运行模型的建立提供可靠的使能信号。 图8 异常数据点准确度 对于其中异常数据点 (xi,yi),利用KNN算法在历史数据库中搜寻K个与故障数据特征xi最近邻的工况点,在此基础上进行KNN加权回归或Ridge回归分析以获得更为精确的预测值。K值的选择对回归分析的结果会产生重大影响,较小的K值其近似误差会变小,但模型变得复杂,容易过拟合,造成估计误差会变大。K值较大时,效果相反。为了获得本文使用数据集的最佳K值,以基于距离的KNN加权回归法计算对异常数据的回归精度为指标,同样使用带有交叉验证的网格搜索法进行寻优,得到如图9所示的K值学习曲线,可知当K=7时,应用KNN距离加权回归法的RMSE和MAPE均为最小值,故对本文中使用的KNN分类器中的超参数K设为7。 图9 不同K值下KNN回归精度 考虑到KNN距离加权回归算法忽略了各特征变量对回归值的影响,故本文对异常数据 (xi,yi)的K个最近邻点数据应用Ridge回归算法进行数据拟合,得到基于Ridge算法的回归值Ridge算法中正则化系数 λ的取值合适,往往能够选择出经验风险与模型复杂度同时较小的模型。利用带有交叉验证的网格搜索法以Ridge算法对异常数据的回归精度为指标对参数 λ进行寻优,得到如图10所示的λ值学习曲线。可知当λ =4时,对异常数据恢复的RMSE和MAPE均为最小值,故将超参数 λ设为4。 图10 不同λ 值下Ridge回归精度 图11 不同数据恢复方法效果对比 使用不同的数据恢复方法对异常数据点恢复效果对比如表5所示。当数据出现异常时,若以数据异常前尾值替代目标变量出口NOx浓度的测量值,异常恢复数据与真实原始数据之间的RMSE、MAPE较大,对于反应较快的工业过程,不能很好的反应过程量的变化,难以实现平稳闭环控制。若使用RBFSVR软测量的预测值替代目标变量测量值,与异常数据原始值之间的 RMSE=4.575 4 mg/(Nm3),MAPE=8.687 9%,其恢复精度相对较低,不能满足高精度可靠控制的要求。使用KNN算法回归值替代测量值时,其回归值为异常点K个近邻工况数据点目标输出变量值的距离加权平均,较软测量模型预测值其数据恢复精度有所提高。在KNN的基础上应用Ridge回归算法进行异常点数据恢复,其考虑了每个特征变量对目标输出变量的影响,恢复的数据与实际原始值之间的 RMSE=1.256 6 mg/(Nm3),MAPE=2.478 9%,与SVR软测量模型相比,回归精度提高6.209%。在工业过程数据出现异常时能够提供更可靠的数据,维持系统短时容错稳定运行。 表5 不同回归算法对故障点数据恢复效果对比 工业过程控制数据的正确性和可靠性对于工业系统安全运行至关重要。本文建立基于RBF-SVR软测量模型实现对目标变量测量值的异常检测,改进工业数据异常时使用软测量值、异常前尾值等替代测量值的方法,利用KNN算法与Ridge回归算法结合实现对异常数据的高精度恢复,并在此基础上构建控制系统容错运行模型。采用电厂实际运行数据进行仿真验证,结果表明,本文所提基于数据驱动的工业过程异常数据检测及容错运行模型,能够准确检测出异常值,对异常数据的恢复精度也高于使用异常前数据尾值、软测量值或KNN加权回归值等数据恢复办法,能够有效应用于对工业过程异常数据的恢复,实现工业生产过程安全、可靠的短时容错控制运行。1.5 容错切换
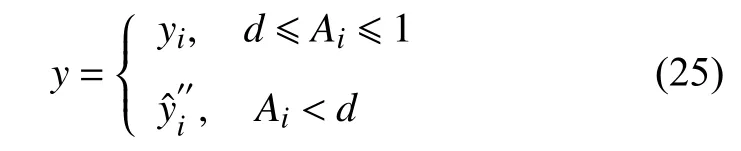
2 仿真验证
2.1 数据获取与变量选择


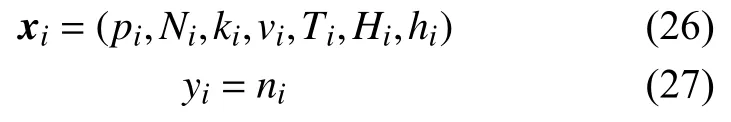
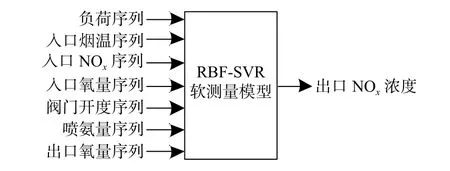
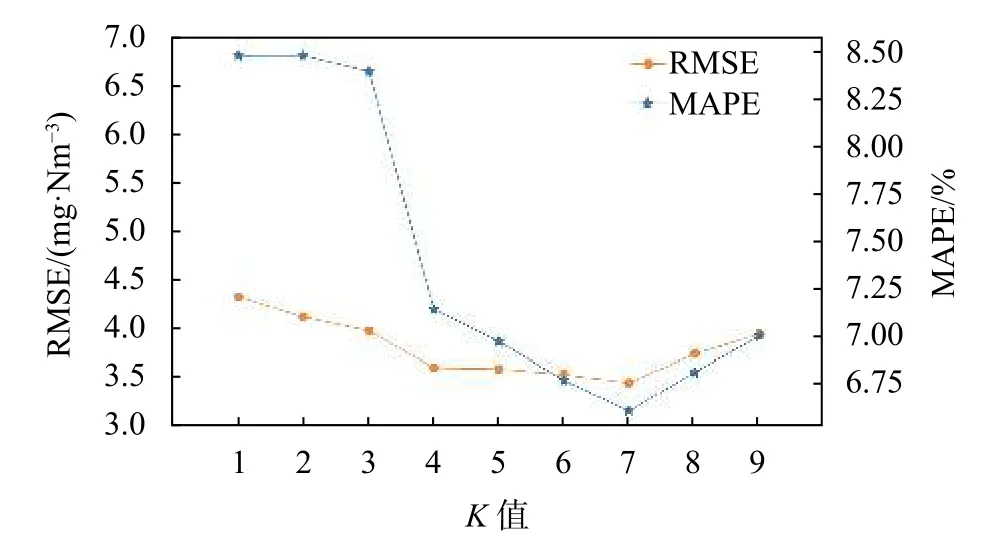
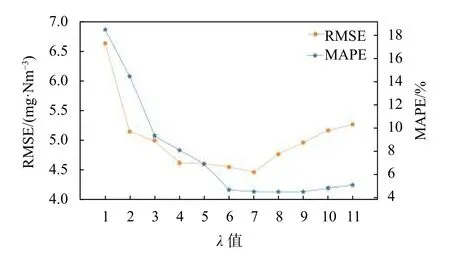
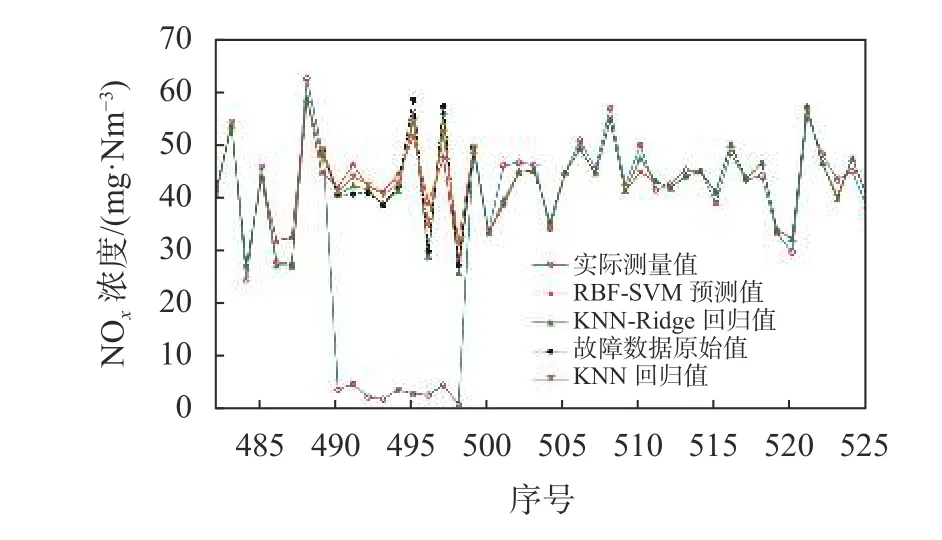
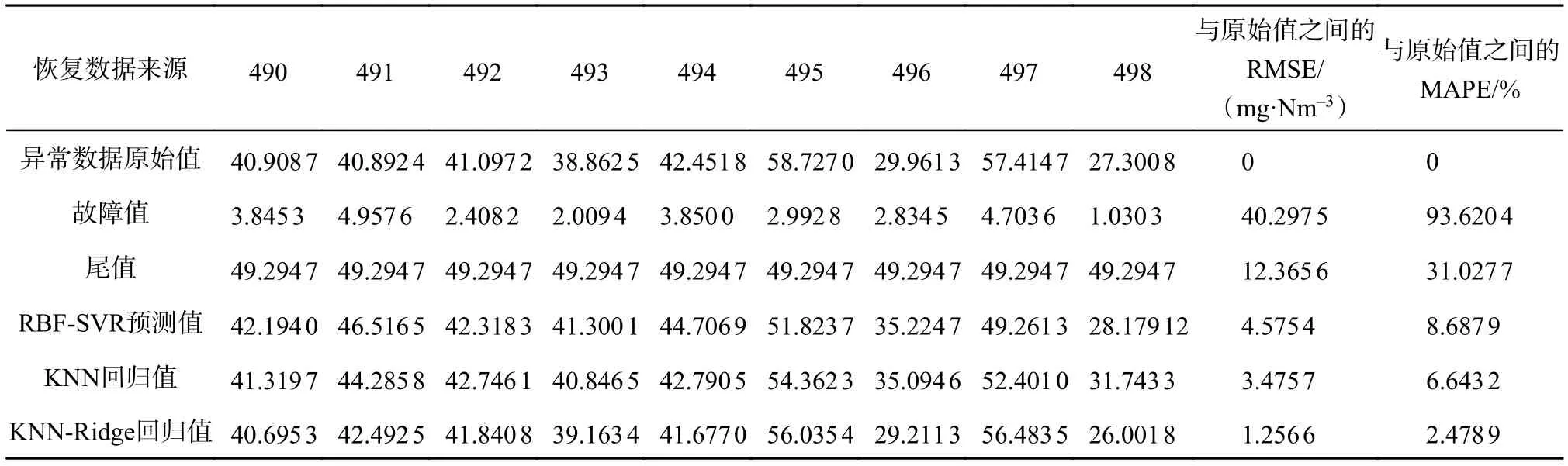
2.2 仿真比较
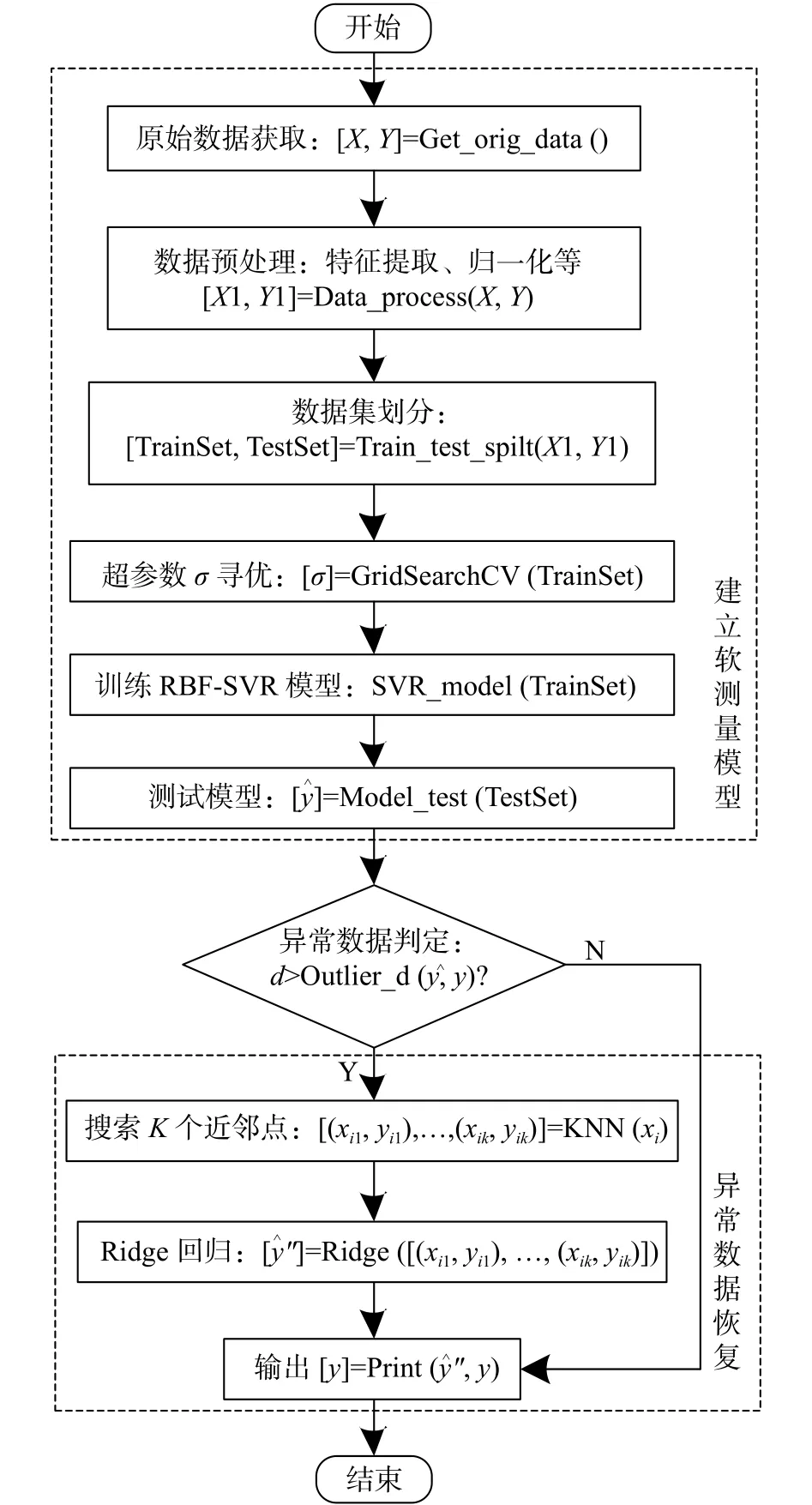

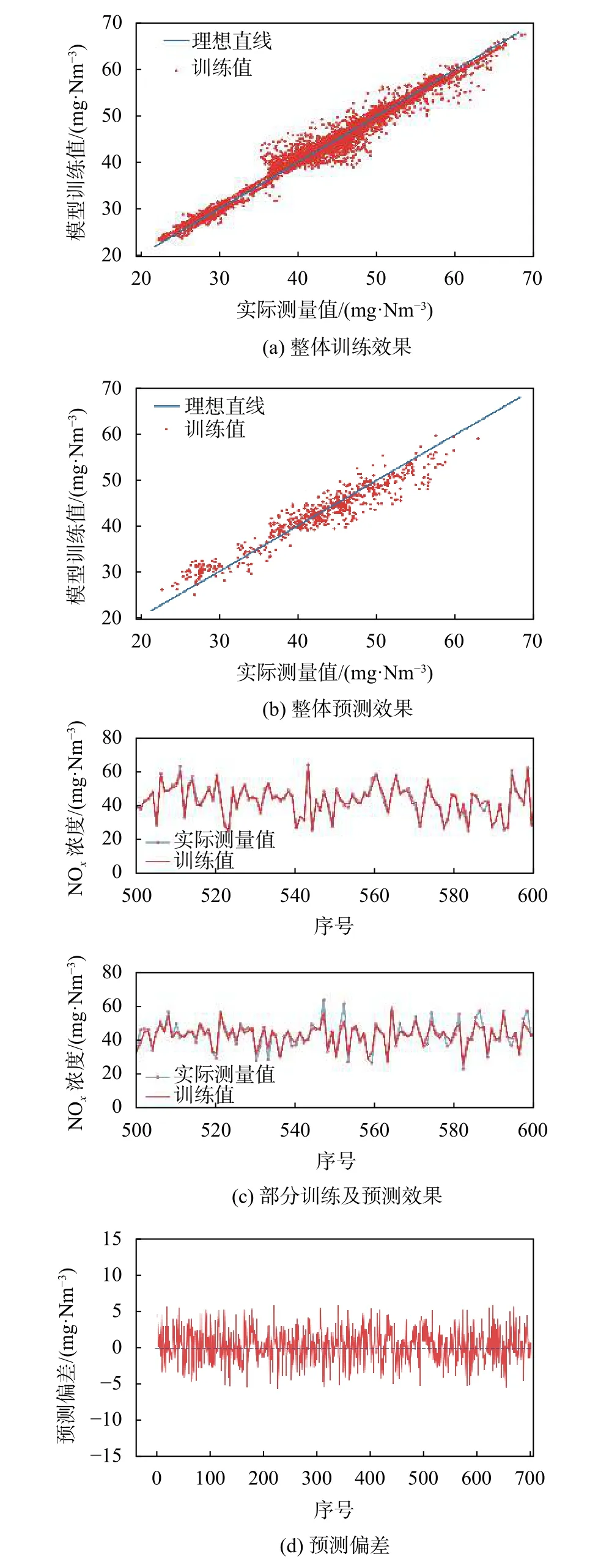


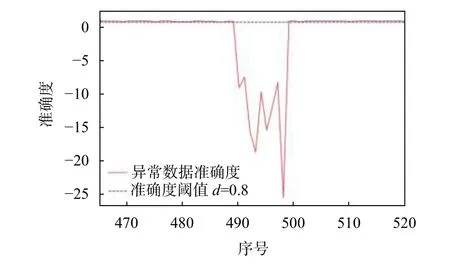
3 结束语
