Alpha-Shapes分段改进算法在三维模拟树枝体积扫描测量中的应用

张 鹤,李东升,陈爱军

(中国计量大学计量测试工程学院，浙江 杭州 310018)

0 引 言

近年来，在国家节能减排政策的大力推动下，我国碳交易市场得到了快速发展，对林业碳汇提出了更高的要求。传统的砍伐式林木生长量计算方法已经无法满足当前碳汇精度的需要。为此，研发一种树木活体材积计量方法正势在必行。本文应用三维激光扫描技术对树干和树枝进行模拟测量，使用的模拟树干和树枝为可精确测量体积的标准管体，这样就给误差评定带来很好的方便性[1]。

由于现有的三维激光扫描仪并不是为专门应用于树木测量设计，而且由于树枝的相互遮挡，利用三维激光点云数据进行树枝内部结构体积参数计算尚存在难点，因此如何获得精确的立木材积量需要应用特殊的算法。目前可用于计算树木体积的三维模型主要有两种：1)几何模型，主要计算树冠外包体积，树木的树枝部分以及树枝分叉内部的黏连体积无法消除，对于分枝特征表现不足，计算得到的结构参数也更加单一，只能计算树木冠层形态，无法全面地获得树木树枝的体积数值[2]；2)体素模型，建立体素模型，将待测区域分割为体素，包含激光点的有效体素个数乘以体素体积即得总体积[3]。这种模型在树枝叶茂密时易受内部点云缺失影响，模型易形成内部空洞，也无法全面地指示树枝体积形态[4]。

基于此，本文提出一种基于Alpha-Shapes的分段改进算法模拟树枝三维体积测量的新方法。其中Alpha-Shapes算法由Edelsbrunner首先提出[5-6]，最初用于点集轮廓的相关构建。目前该算法应用于网格生成、医学图像分析和建筑物外轮廓的边缘提取，但如何将Alpha-Shapes算法应用于提取树干树枝点的点云轮廓，进行树枝三维模型构建并进行体积计算还缺少深入的系统研究[7]。

该方法采用标准塑料直管段、三通管段分叉和四通管段分叉模拟树枝自然情况，使用三维激光扫描系统获取三种塑料管段的三维空间点阵数据，建立模拟树枝的三维模型，利用计算复杂不规则物体体积的Alpha-Shapes算法对三维激光扫描模型进行处理，分段计算出塑料管段体积并以及推导用于树枝体积，有助于提高树木体积的计算精度，为林业碳汇量的计算提供了数据参考[8-11]。

1 Alpha-Shapes分段改进算法原理

基于Alpha-Shapes的分段改进算法主要应用了Alpha-Shapes算法并适当进行了点云数据的分段检测。Alpha-Shapes算法适用于从一堆无序的点集中提取物体的边缘进行包络并可以进一步进行体积计算。包络示意图如图1所示[12]。假设点集中半径为 α的圆由点集内任意两点P1（x1,y1）、P2（x2,y2）唯一确定，若圆内无其他点，则P1、P2为边界点，线段P1P2为边界线段。如图2所示，并可以得到过这两点的圆的圆心P3，即求出与P1点、P2点距离为 α 的点P3（x3、y3）。

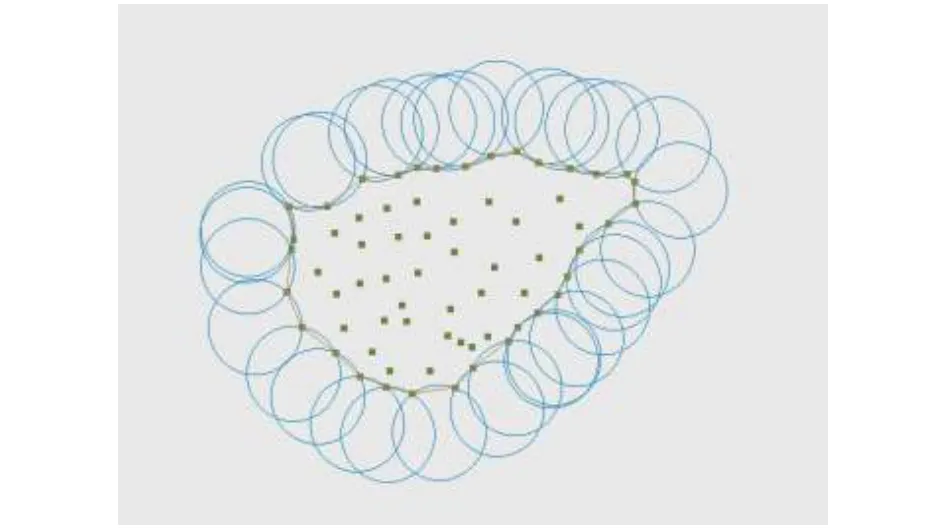
图1 包络示意图

图2 Alpha-Shapes模型示意图

由已有距离交汇算法得：

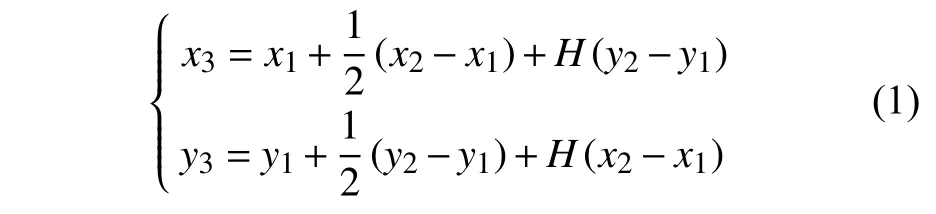
式中：

获得圆心后，通过其他点到圆心的距离是否小于α值，并以此判断P1、P2是否为边界点。若无任何点到圆心的距离小于α值，则P1、P2为边界点，线段P1P2为边界线段[13]。

三维Alpha-Shapes算法的公式原理与二维原理相同，通过三点作半径为α的球来判断边界点，并在得到的边界点处建立三角片面，重构出曲面。该算法可适用于多面体内外轮廓线提取和体积计算，通过对α值的设定，来控制轮廓线的精细程度[14-15]。对于凹多边多面体，如分叉树枝部分，需要考虑凹边拐角处和内部情况，若α值设定不合理，则拐角分叉处会被钝化引起严重变形，故α值应根据实际情况进行取值[16]。

使用Alpha-Shapes算法进行边缘检测以及体积计算的时候，会产生黏连现象，因此在Z轴上采用分段算法进行体积分割计算。点Pi（Xi，Yi，Zi）（i=1,2,···,n，n为Z轴坐标点的总数）坐标范围为Zmin～Zmax，按照Z轴方向以及一定高度β值对数据分段，则任意一点P（Xi，Yi，Zi）在Z轴分段的序号为

式中：β——分段高度；

Ci——Pi点以Z轴为分段方向的序号。

在分段过程中在最高层处可能存在数据不足、数据缺失等问题，因此需要对最高层点云进行点云数据判断并对于最高层点云数量不足的地方加以调整。公式可表示为

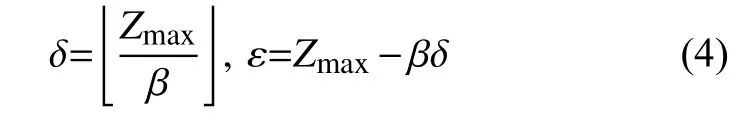
式中：δ——Z轴点经过高度为β值的分段后剩余不足为一段的点数；

ε——满足一个分段需要补足的点数[17]。

在δ个点中进行坐标比较，选取Z坐标值最大值，也就是最高层处进行补点，补充ε个与最高层重合的点，这样既不会改变扫描目标的建模形状，也能够补足点云数量，让点云数据足以分段。点云数据补充完整后则可以进行体积分段计算，按分段的序号依次进行体积计算，最后将体积累加。

Alpha-Shapes分段改进算法体积计算过程时选择合适的检测半径α值和分段高度β值是一个重要问题[18]。检测半径α值和分段高度β值的大小将直接影响点云数据建模精度和体积计算误差。因此，在实际的应用中需要在点云数据建模精度和体积计算误差之间寻找一个平衡点，使其达到最好的计算效果。

2 实验设计

针对树枝建模及体积模拟，因树枝情况复杂，体积分散，不便于验证算法误差值。综合考虑采用标准塑料直管段对树干进行模拟，采用三通管段和四通管段对树枝的分叉情况进行模拟。

三维扫描实验如图3所示，在进行三维点云扫描实验时，对上述管段进行竖直放置，并调整三维激光扫描仪和标靶的位置，其中标靶作为点云数据拼接的基准，其放置位置尤为重要，不仅影响站点布设的数量，同时也影响拼接精度。标靶应为3个，布置在公共扫描区域内，呈锐角三角形放置。在标靶布设过程中，需要根据测量精度要求控制标靶与扫描仪之间的距离，本实验设计标靶与扫描仪之间的距离为30～60 cm。同时避免将3个标靶放置在同一直线上。记录相应的位置坐标以便于后续实验数据处理。

图3 三维扫描实验图

本文以瑞士徕卡HDS7000三维激光扫描仪作为数据获取平台，采用基于标靶采集的方法进行三维扫描实验：首先设置扫描密度为高等分辨率得到点云数据，并利用Cyclone软件完成点云数据的拼接，处理点云数据，删除噪声点，在点云中确定扫描目标的起止点高度并记录，最后将处理好点云坐标数据文件以txt格式导出。

以直径为50 mm的标准塑料直管段为例，样本的真实照片和扫描处理后得出的管段点云数据如图4所示。得到管段点云数据后则导入Matlab中间进行体积计算与验证。

图4 标准塑料直管段点云数据图

3 实验数据分析

本试验针对50 mm直径标准塑料直管段、标准三通管段、标准四通管段模拟树枝分叉进行三维激光扫描实验，并分别设置Alpha-Shapes算法半径参数α以及分段高度包含的激光点数β进行体积计算，并得到体积值V，并对其中产生的单层误差体积值V1′及其累计误差和体积值误差 ∆V1进行分析。

首先分析在使用标准塑料三通管段和四通管段进行模拟树枝分叉扫描试验时出现的黏连问题和镂空现象，由于标准塑料三通管段和四通管段的黏连问题和镂空现象原理相同，故此处仅分析标准塑料三通管段。

对标准塑料三通管段和四通管段进行体积计算时，β2值不变，当α2值较大时，在标准塑料三通管段分叉处会产生黏连问题，造成三维模型体积值V2增大，如图5（a）所示；当α2值较小时，因点云数据只存在于标准塑料三通管段分叉表面，扫描得到的三维模型孔隙随之加大，产生镂空的现象，造成V2减小，如图5（b）所示。因此，当α2取值较大或较小时，最终会导致体积值误差 ∆V2增加，需选取合适的α2值来降低黏连问题或镂空现象造成的 ∆V2，如图5（c）所示。

图5 不同β2值与α2值的三通管段建模示意图

α2值不变，β2值改变时，当β2值增大时，三维建模受到噪声点影响随之增加，且在分叉处会产生较大黏连问题，如图5（d）所示；当β2值减小时，分段计算次数随之增多，会导致单层误差体积值V2′值叠加，误差增大，且建模也会因分段次数过多而不清晰从而导致 ∆V2增大，如图5（e）所示。由此可知，当β2值取值较大或较小时，最终会导致 ∆V2增加，因此需选用合适的β2值来减低噪声点影响或建模不清晰造成的体积值误差，如图5（f）所示。

3.1 标准塑料直管段实验

针对标准塑料直管段，进行三维扫描实验，建立三维模型并得到标准塑料直管段三维点坐标数据，输入Matlab中设置不同α1值以及β1值进行Alpha-Shapes算法的体积计算，得到数据如表1所示。

表1 标准直管段不同α1值和β1值以及对应体积值V1 10-3 m3

由表1可知，对标准塑料直道进行计算时，β1值不变，α1大于0.25则误差过大不予讨论。当α1值由0.25向0.1变化时，随着α1值减小则单层体积间隙会更明显,V1′相对会增加，因此 ∆V1随着 α1的减小而增加；当 α1值由0.1向0.05变化时,∆V1变化幅度较小，此时Alpha-Shapes算法计算体积较稳定，受噪声点影响较小，由此可知该范围是α1最佳取值范围；而当α1值由0.05向0.025变化时，∆V1在不同β1值中呈现误差都较大，误差值在0.935～0.999之间，由于镂空现象造成体积值V1减少，因此产生较大 ∆V1。

α1值不变，β1值改变时，因无分叉影响，所以分段会造成较大误差，所以 ∆V1随着β1值的增加而增加。

通过Alpha-Shapes算法计算α1值取不同值，β1值取不分段的整体的体积值Vz1，进行单层误差体积值计算，公式可表示为：

式中：i——计算体积值V1时的分段次数；

V1′——单层误差体积值。

计算后绘制不同α1值以及β1值情况下的V1′值折线图如图6所示。

图6 标准直段各分段单层误差体积值V1′折线图

由图6可知，β1值不变，α1值改变时，单层误差体积值V1′随 α1值的减小而减小。α1值由 0.25 向0.1 变化时，V1值变化趋势较明显；α1值由0.075向0.05变化时，V1值变化平稳，并能取得V1′最小值；α1由0.05向0.025变化时,V1′值接近1，此时体积值误差较大，予以舍去。

α1值不变，β1值改变时,V1′随 β1值的减小而减小。β1值在100～500间时,V1′值较小，但由于分段次数过多，会导致V1′累计误差增大,∆V1增大；β1值在500～700间时，V1值变化较平稳；β1值在700～1 100间时，V1值变化较大。

综上所述，对标准塑料直管段模拟树干进行体积计算时，α1值由0.075向0.05变化，β1值在500～700范围内变化时，体积值V1计算较为理想,V1′变化较平稳,∆V1较小。

3.2 标准三通管段与四通管段模拟树枝分叉实验

标准塑料三通管段与四通管段模拟树枝分叉实物图如图7所示，三通管段进行三维扫描实验并经过体积计算后可得体积值V2，数据如表2所示。四通管段进行三维扫描实验并经过体积计算后可得体积值V3，数据如表3所示。

图7 标准三通管段与四通管段模拟树枝分叉实物图

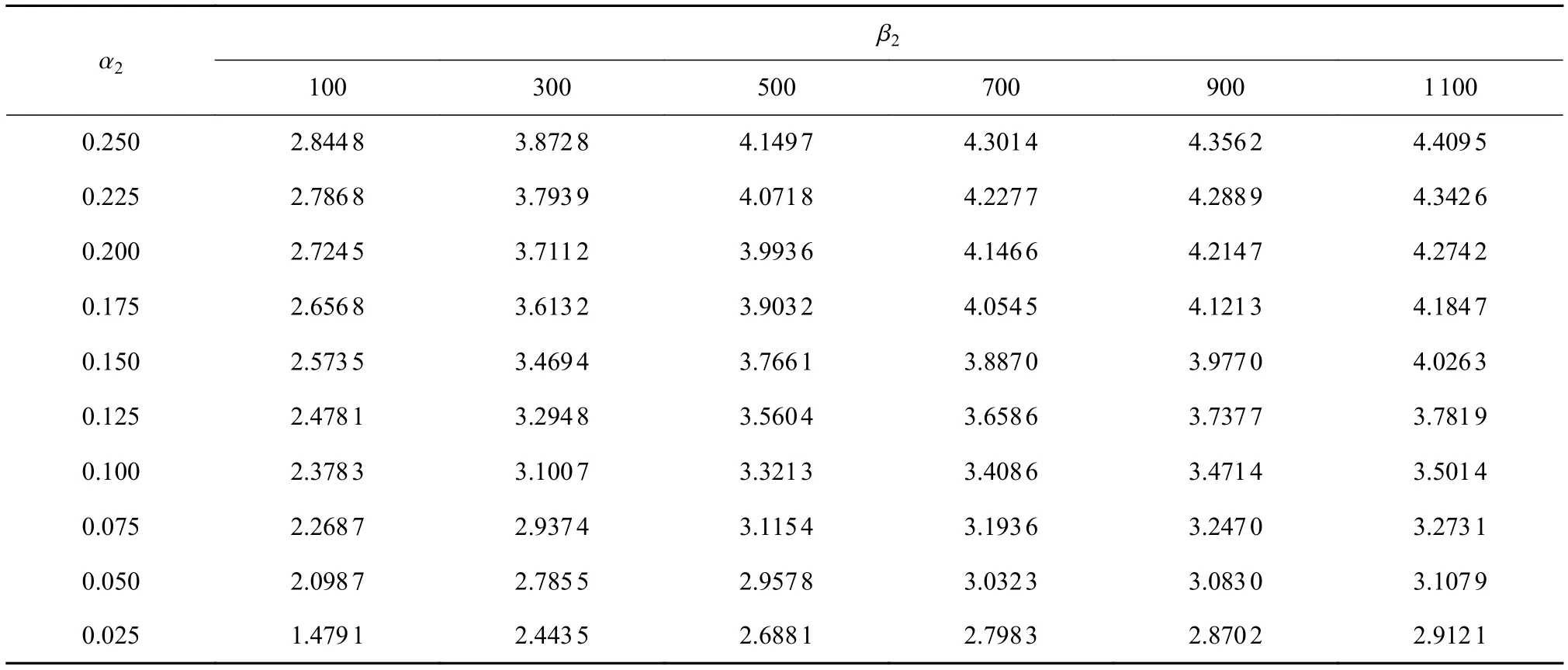
表2 标准三通管段不同α2值和β2值以及对应体积值V2 10-3 m3

表3 标准四通管段模拟树枝不同α3值和β3值以及对应体积值V3 10-3 m3

由附录表2可知，在三通管段数据中，当β2值在100～500范围内变化时，由于黏连问题使得V2增加,V2′的累计使得V2减小，此时受V2′累计误差的影响较大，因此整体体积偏小。当α2值在0.25～0.1范围内变化时,∆V2较小是因为分叉处黏连问题增加的体积抵消了因V2′累计误差而减小的体积，但黏连问题和V2′累积问题并没有减小，因此该α2值范围不能采用；当α2值由0.1向0.025变化时，由于镂空现象造成 ∆V2较大，不能采用。

当β2值在500～1 100范围内变化时，此时受V2′累计误差的影响较小，受黏连问题的影响较大，V2偏大，可以通过改变α2值进行修正。当α2值由0.25向0.075变化时,∆V2较大，但随着 α2值的减小而降低；当α2值由0.075向0.05变化时，三维建模黏连问题较小,∆V2较小；当 α2值由0.05向0.025变化时，由于镂空现象造成 ∆V2较大，不能采用。

而由表3可知，在四通管段数据中，α3值与β3值的变化情况与三通管段数据变化情况相同，则不再赘述。

同理，通过Alpha-Shapes算法计算三通管段α2值取不同值，β2值取不分段的整体的体积值Vz2，进行V2′计算并绘制折线图，如图8所示。而四通管段的单层误差体积值V3′如图9所示。

图8 标准塑料三通管段各个单层误差值V2′折线图

图9 标准塑料四通管段各个分段单层误差体积值V3′折线图

由图 8（a）可知，β2值不变，当 α2在 10～0.25 范围内变化时，单层误差体积值值V2′随α2的减小而减小；当α2值由0.25向0.025变化时,V2′趋于稳定，因此对该范围着重分析。如图8（b），当α2由0.25向 0.075变化时,V2′持续下降，当 α2由 0.075向0.05变化时,V2′趋于稳定。当α2由0.05向0.025变化时,V2′陡然减小。

α2值不变,V2′随 β2值减小而减小，综合对比，当 β2值700～900范围内变化时,V2′值在不同 α2取值值中都比较稳定,∆V2较小。

综上所述，对标准塑料三通管段模拟树枝分叉进行体积计算时，在分叉处选用合适的β值进行体积计算能有效减小体积值误差，因此，β2值在700～900范围内变化，α2值由0.075向0.05变化时，V2计算较为理想,V2′累计误差影响较小,∆V2较小。

同理可得，对标准塑料四通管段模拟树枝分叉进行体积计算时，在分叉处选用合适的β3值进行体积计算能有效减小体积值误差 ∆V3。因此，β3值在700～900范围内变化，α3值由0.075向0.05变化时，V3计算较为理想,V3′累计误差影响较小,∆V3较小。

3.3 真实分叉树枝实验

本次实验对真实树枝进行扫描，实物图和扫描图如图10所示，通过三维扫描实验并进行体积计算后可得体积值V4，数据如表4所示。

图10 真实树枝实物与三维扫描图

表4 真实树枝不同α4值和β4值以及对应体积值V4 10-3 m3

由表4可知，V4的变化趋势与标准塑料三通管段和四通管段的体积值变化相似。当β4值在100～500范围内变化时，体积值误差 ∆V4较大，而且综合考虑镂空现象以及黏连现象，则该范围不能采用。而当β4值在500～1 100范围内变化时，此时受单层误差体积值V4′累计误差的影响较小，当α4值由0.1向0.05变化时，三维建模黏连问题较小，体积值误差 ∆V4较小。

同理，通过Alpha-Shapes算法计算α4值取不同值，β4值取不分段的整体的体积值Vz4，进行单层误差体积值V4′计算并绘制折线图，如图11所示。

图11 真实树枝各个分段单层误差体积值折线图

由图 11可知，当α4由 0.25向0.075变化时，V4′持续下降，当 α4由0.075向0.05变化时,V4′趋势较理想。当α4由0.05向0.025变化时,V4′陡然变化并减小。

α4值不变,V4′随 β4值减小而减小，综合对比，当 β4值700～900范围内变化时,V4′值在不同 α3取值中均比较稳定,∆V4较小。

综上所述，对真实树枝分叉进行体积计算时，体积计算情况、α4值与β4值范围选取以及误差分布情况与标准塑料三通管段和四通管段的情况相似，说明该算法在真实树木扫描体积计算中也能够参考应用。

3.4 体积值误差分析

针对不同α值和β值情况下，标准塑料直管段、标准塑料三通管段和四通管段以及真实树枝的体积值误差如图12所示。

图12 各个塑料管段以及真实树枝误差体积值∆V折线图

由图12(a)可知，在标准塑料直管段的体积计算中当 β1取值在 100～1 100 间，随着 α1从 0.025～0.25间取值的增加而 ∆V1增加，当α1值由0.075向0.05变化时,∆V1变化幅度较小。而当 β1取值在700～900间时,∆V1变化幅度最小，而且 ∆V1也较小，因此此时为7.46%最佳值。

由图12(b) (c)（d）可知标准塑料三通管段和四通管段、真实树枝的体积计算中，当β值在100～500范围内，α值由0.25向0.1变化时，分叉处黏连问题增加的体积抵消了因V′累计误差而减小的体积，使得体积值误差 ∆V较小，但黏连问题和V′累积问题并没有减小因此该范围不能采用；当α值由0.1向0.025变化时，由于镂空现象造成∆V较大，不能采用。当β值在500～1 100范围内变化时，当α2值由0.25向0.075变化时,∆V较大，但随着α值的减小而降低；当α值由0.075向0.05变化时，黏连问题较小，∆V较小；当α值由0.05向0.025变化时，由于镂空现象造成 ∆V较大，不能采用。而当β值在700～900范围内变化，α值由0.075向0.05变化时,∆V取得最小值，范围为4%～5%。

除了黏连现象和镂空现象等建模算法造成的误差外，在三维扫描时产生的噪声点在体积计算时也会造成体积值误差，而且在标准塑料管道以及真实树枝的边缘部分会产生边缘性误差造成点云数据不准确，边缘提前错误等问题。在后期工作中可以在误差的减小方面进行进一步研究。

4 结束语

本文提出的Alpha-Shapes分段改进算法，通过标准塑料直管段模拟树干实验分析可知,∆V1随β1值增加而增加，α1值在 0.05～0.075 间，β1值在 700～900间能得到较好的V1；通过标准塑料三通管段和四通管段模拟树枝分叉实验分析可知，在分叉处选用合适的α2、β2和α3、β3值进行体积计算能得到较好的体积值V2和V3，同时降低黏连问题和镂空现象的影响，减少V2′和V3′的累积误差，有效减小∆V2和 ∆V3，由实验数据可知，β2和 β3值在700～900间，α2和α3值在0.05～0.075间时能得到较好的V2和V3，得到的体积误差值在4%～5%之间。通过对真实树枝的实验分析可知真实树枝分叉部分附和标准塑料三通管段和四通管段选取实验最佳参数。

利用Alpha-Shapes分段改进算法对标准塑料直管段、三通管段和四通管段以及真实树枝进行三维重建时，在α值和β值变化过程中，构建的三维模型也在有规律地变化。可以看出，不同α值和β值构建的三维模型能够反映树枝树干的空间伸展形态、曲面体积、分枝特性及分叉处规则性等结构参数，研究结果可作为树枝树干结构体积计算的研究基础。