基于多元自适应回归样条的页岩密度计算模型

欧传根 唐 诚 王崇敬 梁 波

(中石化西南石油工程有限公司地质录井分公司)

0 引 言

页岩气是近年来的勘探开发热点，在页岩气解释评价方面已经开展了大量的工作，普遍认为含气页岩储集层的典型响应特征具有高自然伽马、低岩石密度的特征,并广泛应用密度、中子、伽马能谱、电阻率等测井项目来评价地层孔隙度、含气饱和度、有机碳含量,获取镜质体反射率Ro、计算矿物组分体积含量等[1-2]。这些方法和技术的应用，表明页岩密度是用来开展页岩气甜点评价的重要依据和关键参数之一。由于页岩气开发的“降本增效”原因，且一般采用水平井施工，水平井段普遍达到1 500 m以上，放射性测井的井下安全风险极大，绝大部分水平井取消了岩石密度测井项目，部分工区的开发井也取消了测井项目，仅依靠随钻伽马测井资料与气测录井资料开展储集层评价等工作，导致测试选层时缺乏可靠的评价依据。针对上述问题，开展页岩地层岩石密度录井计算方法研究，既可为页岩气井的储集层评价、测试选层提供依据，也可为其他类型油气层的解释评价参数求取提供借鉴。

1 页岩密度求取方法研究进展

在钻探现场，直接获取岩石密度的方法有密度测井与岩石密度录井两种，井下安全与降低成本等多重原因导致水平井普遍取消了密度测井项目。岩石密度录井主要通过计量岩屑排出液体的体积来计算密度，但由于岩屑普遍细小，测量有一定的误差，在页岩气井中基本没有得到应用。

间接获取岩石密度的方法主要由地球物理方法发展而来，如Gardner经验公式根据声波速度来拟合岩石密度，该算法在物探领域应用范围极广，但存在明显的误差。王盼等[3]在该经验公式的基础上加入电阻率与自然伽马数据，形成了优化算法，取得了较好的应用效果，但该方法需要较多的测井数据，在不测井的页岩气水平井中无法应用。

目前最常用的密度计算方法从ECS测井方法发展而来。Herron等[4]应用氧闭合模型将地层中元素含量转换成氧化物，根据氧化物的质量或元素的质量，利用统计公式建立元素与矿物含量之间的关系，因为每种矿物对应固定的骨架密度，所以可根据地层中矿物类型和含量求出地层骨架密度，模型计算公式为：

式中：ρ为地层密度，g/cm3；m为地层中矿物的种类；ρi为第i种矿物对应的骨架密度，g/cm3；Mi为地层中第i种矿物的百分含量，%。

该模型实质是线性模型，制约精度的关键在于矿物种类及含量的准确获取。孙建孟等[5]通过广义逆矩阵优化了元素与矿物的转换模型，廖东良、赵子斌等[6-7]在此基础上，开展了矿物类型约束、相对密度加权、反演评价等优化工作，获得的地层骨架密度计算模型更符合地区特点。

顾炎午等[8]借鉴ECS测井计算模型，开展元素录井数据多元线性回归方法研究，建立利用元素计算岩石密度的数学模型，很大程度上缓解了测井项目少、页岩气评价参数匮乏的困境。但是，岩石的密度与岩石骨架成分之间存在复杂的非线性关系[6]，而多元统计回归模型为线性回归模型，故计算精度难以进一步得到提高，同时计算模型的可推广性与可移植性也有待提高,该模型在四川盆地A井应用时相关系数达到0.8，移植到B井时，计算结果与实测数据相关系数大幅度降低到0.71。因此，有必要进一步开展计算方法的研究，建立精度更高的数学模型，便于推广应用。

2 多元自适应回归样条算法简介

多元自适应回归样条(Multivariate Adaptive Regression Splines,以下简称为MARS)是机器学习算法中的一种，属于能自适应处理高维数据的样条回归方法[9-11]。MARS方法的本质是将每一个预测变量(输入参数)设定一个切分点拆成两组，然后在每一组中建立预测变量与结果变量的关系，形成一对铰链函数，其数学模型为：

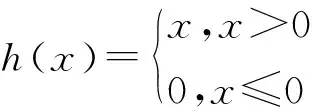
一对铰链函数通常写成h(x-a)和h(a-x)，其中x是预测变量，a是该变量的切分点。如果存在两个变量x1和x2，且x1对预测结果的影响与x2有关，则称之为变量的交互项，用x1*x2表示，其铰链函数通常写作h(x1-a)*h(x2-b)的形式，a、b分别为变量x1、x2的切分点。针对每一个变量形成铰链函数，建立分段线性模型，每个铰链函数拟合原始数据的一部分，且相互不产生影响。通过反复的穷举搜索，寻找拟合最好的切分点，完成全部预测变量的拟合以后，移除对模型没有显著贡献的变量，可优选出最合适的模型。在所有机器学习算法中，MARS方法有一定的计算量，但相对而言计算快捷，并且不需要太多的数据预处理以及变量的筛选，还能够捕捉变量之间的非线性和交互作用[10]。

页岩岩石中不同元素之间存在多重共线性等复杂的关系[4,8]，如Al与K元素存在明显的正相关性，Si、Ca、Al之间此消彼长的现象较为明显，元素与岩石密度之间也存在复杂的非线性关系，因此从理论上分析，MARS方法较多元线性回归等方法更具优势。

3 基于MARS方法的计算模型研究

本次研究选取四川盆地页岩气井Y井的XRF元素录井数据、ECS测井及分析化验资料为基础，开展计算模型的研究。

3.1 输入变量与调优参数

XRF元素录井能获取20多种常见的元素含量，但页岩中常见的元素只有10余种。斯伦贝谢公司的ECS或Litho Scanner测井能提供9种元素的分析结果，其中元素录井与测井均能提供的元素数据只有8种(Mg、Al、Si、S、K、Ca、Ti、Fe)。由于其他元素的含量极低，同时也为了便于对比，统一设定输入参数为这8种元素，同时统一按ECS测井数据格式，将元素录井的数值转换为小于1的小数。

MARS方法需要设定两个调优参数，为预测变量的阶数和保留特征的项数，分别称之为degree和nprune。degree为≥1的整数，Hastie等[10-11]推荐给degree设定一个上限(如≤3)，因较高的阶数会导致计算量大幅度增加，并导致数值大幅度膨胀或缩小，故不宜取值过大;nprune一般取值≥2，当变量数少于10个时，其上限建议为20。在综合分析后将调优参数degree设定为1～5，nprune设定为2～20，一共形成90个MARS模型。

3.2 计算模型

设定参数后进行模型的训练，由于建立了90个MARS模型，采用K折交叉验证方法从中选择最优模型[10-11]，获得最优模型的决定系数r2=0.85，调优参数degree=2，nprune=17，铰链函数及其系数如表1所示。

从表1最终的模型以及图1中元素与密度的关系分析，8种元素中仅有6种参与了模型计算。对密度数值影响较为明显的元素是Ca、Si、Fe，并且不是简单的线性关系，Ca、Fe、K、Si元素均表现为分段式的影响，Ca元素甚至在不同的含量区间内，对密度的影响关系存在明显反转现象，Al、S两种元素与密度整体呈微弱的负相关，Mg、Ti两种元素的含量变化对密度基本没有影响。

表1 基于MARS的页岩密度计算模型系数

同时，MARS模型揭示了元素之间存在相互影响，Al、Si元素之间，Al、Ca、Fe与S元素之间存在交互影响，证实了元素与密度之间存在复杂的非线性关系，因而采用简单的线性模型难以取得较好的计算效果。

3.3 结果对比

Y井3 433.00～3 864.00 m井段实测密度2.30～2.71 g/cm3，平均2.63 g/cm3。分别用多元回归模型、MARS模型以及Herron等公开的ECS计算模型[4-5](以下简称为Herron模型)进行计算，将获得的结果与实测的页岩密度进行对比可知，3种模型的效果有显著的差异(图2)。

MARS模型的效果最好，岩石密度计算结果为2.31～2.72 g/cm3，平均值2.63 g/cm3，计算结果与实测数据之间没有明显的偏差，r2=0.85。多元回归模型也有一定的效果，计算结果为2.38～2.70 g/cm3，平均值2.65 g/cm3，计算结果普遍略高于实测结果，r2=0.71。效果最不理想的是Herron模型，该模型的计算结果为2.66～2.75 g/cm3，平均值2.72 g/cm3，计算结果与实测数据在数值的绝对值方面有较大的差异，变化趋势方面具有微弱的正相关性(r2=0.0356)，可能与其模型建立时间早，建立模型的数据主要来源于北美地区，没有考虑到地区之间的差异有一定关系。对比结果表明MARS模型的计算结果较为可靠，能满足后期的页岩气甜点评价需求。

图1 基于MARS方法的岩石密度与8种元素间的相关关系

图2 Y井3种模型计算结果的相关性对比

4 应用效果

将研究建立的MARS模型在四川地区的Z井进行了应用。Z井为水平井，其大斜度段与水平井段为3 750.00～5 450.00 m，钻后未测井，仅有一条随钻伽马曲线，且该伽马曲线为两种工具测量，井深4 105.00 m以上为旋转导向工具提供的随钻伽马，测值490～805 API，后续井段为LWD工具测量，测值165～418 API，测值有明显差异。由于使用了不同的随钻工具，钻时与气测值也有明显的波动，旋转导向工具应用井段的气测全烃值4.851%～24.380%，平均16.509%，钻时3～24 min/m，平均8.5 min/m。使用LWD滑动工具井段气测全烃值4.873%～37.359%，平均13.338%，钻时3～42 min/m，平均15.6 min/m。外部环境的变化导致直接应用气测、钻时、随钻伽马评价储集层的难度加大。

图3 Z井3 750.00～5 450.00 m井段计算效果图

通过应用MARS模型计算出地层密度(图3)，全井段密度2.32～2.66 g/cm3，平均2.50 g/cm3，全井目的层可以分为4个层段。第一段井深3 750.00～3 850.00 m为入窗井段，气测值出现异常，全烃0.868%～15.021%，平均7.070%，计算页岩密度为2.66～2.52 g/cm3，密度开始下降的位置与气测明显升高的位置吻合，整体而言气测值有异常但数值不高，页岩密度较高，储集层的含气性一般。第二段井深3 850.00～4 694.00 m，气测全烃值6.194%～24.380%，平均13.274%，计算岩石密度一般在2.45～2.54 g/cm3之间，平均2.49 g/cm3，个别井深出现高值达到2.61 g/cm3，但高值不延续，推测为岩屑混杂，造成元素录井数据出现波动，导致计算结果随之波动，出现波动的数据点仅有2处，不影响整段的评价，整个井段气测值明显增加，页岩密度为明显的低值，表明地层的含气性较好。第三段为井深4 694.00～4 884.00 m，气测全烃值为9.139%～37.359%，平均24.467%，井深4 850.00～4 855.00 m出现异常低值，全烃仅为7.723%，对应井段的钻时较高达到29 min/m，为平均钻时的2倍以上，反映了高钻时是气测值变低的影响因素，而不是地层含气性有明显变化。计算岩石密度为2.32～2.51 g/cm3，平均2.42 g/cm3，密度明显低于其余井段，表明该段含气性最好，与气测录井结果较为吻合，是本井的最优储集层。第四段井深4 884.00～5 450.00 m，气测全烃值4.875%～20.706%，平均12.075%，计算页岩密度2.45～2.53 g/cm3，平均2.49 g/cm3，气测全烃值较高，页岩密度较低，井段的含气性较好，与第二段基本相当。

从全井段来分析，单独根据气测、钻时难以开展储集层分段，但通过计算页岩密度，能有效地区分出最优储集层与一般储集层，且页岩密度计算值与其他录井数据可以相互补充与印证，在当前页岩气井不测井或测井项目少的情况下，为页岩气甜点评价提供了可靠的评价依据。

5 认识与建议

(1)页岩密度是开展页岩气甜点评价的重要参数，但因大量的页岩气开发井不开展密度测井，甚至不测井，导致评价参数匮乏。基于多元自适应回归样条算法，建立了页岩密度计算模型，为页岩气储集层评价提供了更多的依据。

(2)通过对比与应用，基于多元自适应回归样条算法的密度计算模型提供的结果较为可靠，计算精度较多元回归模型有明显提高，结合常规录井数据，在水平井分段评价方面具有较好的应用效果。

(3)元素录井获取了地层丰富的信息，但数据的应用还不够充分，机器学习算法在解决非线性、复杂模型的建模过程中具有明显优势，有必要进一步加强数学算法在录井数据应用过程中的方法研究，挖掘更多录井数据的价值。