基于区块链的密封式投标拍卖方案

李 蓓，张问银，王九如，赵 伟，王海峰

（1.山东科技大学计算机科学与工程学院，山东青岛 266000；2.临沂大学信息科学与工程学院，山东临沂 276000）

0 引言

随着互联网技术和电子商务的迅速发展，电子拍卖已经成为人们拍卖商品的一种方式。网络拍卖平台为买卖双方提供一个公平交易的拍卖环境，节省了大量的时间和成本，但其隐私性和安全性问题也越来越突出。传统的电子拍卖有四种主要的拍卖方式：第一价格密封投标拍卖、第二价格密封投标拍卖（Vickrey 拍卖）、公开升价拍卖（英式拍卖）以及公开降价拍卖（荷式拍卖）。电子拍卖根据竞拍价是否公开分为密封式投标拍卖和公开拍卖。密封式投标拍卖是指在规定时间内由竞买人秘密地提交标书，在规定时间后才能打开投标并根据拍卖规则选出中标者。在密封式投标拍卖中，除了中标者的标价被公开以外，其余竞买人的报价都保密，可以有效保护竞买人身份的匿名性和标价的隐私性，在当今社会是应用广泛的拍卖方式。本文讨论的方案属于第一价格的密封式投标拍卖。为了保证密封式投标拍卖的安全性，需要满足以下基本特性：

1）正确性。拍卖必须保证能产生最高价格的中标者。

2）公平性。保证参与拍卖的竞买人的地位相同，获得信息一致，是否中标只与出价高低有关。

3）密封性。在打开标书前，无法通过别的方式获取价格。

4）不可否认性。中标者在竞标成功后不可以对自己的出价进行否认。

5）可验证性。任何人都可以验证中标者的身份。

6）时限性。在规定时间前提交标书才能有效参与拍卖，并且在提交标书后在规定时间后才能统一打开标书。

7）不可伪造性。任何人不能用伪造的身份参与竞拍活动。

目前针对密封式投标拍卖已经存在大量研究。Brandt［1-2］设计了一个无第三方参与的密封电子拍卖协议，协议有效去除了第三方，可以很好地保护竞标者的隐私；但由于所有计算都需拍卖人自己完成，具有计算量和通信量较大以及效率不高的问题。Bogetoft 等［3］提出使用基于线性秘密共享的安全多方计算取代可信第三方来构建安全拍卖协议，但该方案需要至少15轮交互。Wu等［4］提出了新的密封式电子拍卖，虽然该方案去除了第三方，但是交互过程也比较繁琐。Lee等［5］和Sun 等［6］分别设计出了基于群签名的密封电子拍卖协议及改进方案。王鑫等［7］利用基于身份的群签名方案和可验证的秘密共享协议，设计了一个密封式的电子拍卖方案，该方案实现了投标者的匿名性、强壮性、中标者的不可抵赖性、公开可验证性和标价的保密性等一般性的安全要求。程文娟等［8］提出一个基于不可信第三方的密封式电子拍卖方案，采用了数字签名技术对竞买人的身份进行验证，从而保护竞买人身份。在计算成交价时，基于离散对数求解的困难性，对竞拍价的二进制长度进行加密封装，以保证竞拍价的秘密性以及结果的正确性。曹刚［9］通过改造Bit 承诺协议，将盲签名技术应用于Bit 承诺协议的生成阶段，设计了一种密封式的电子拍卖方案。目前，大多数的密封式电子拍卖都依赖于第三方去管理和验证拍卖者的身份信息；但是，现实中无法保证存在完全可信的第三方，一旦第三方不诚实或者与竞买人勾结，将会违反拍卖的公平性，并且威胁到其他竞买人隐私和利益。

而随着区块链技术的不断发展，越来越多的研究尝试通过将区块链作为基础设施，利用区块链的特性，实现拍卖的公开透明性、不可篡改性等。区块链作为一个公开透明的账本，所具有的分布式容错、不可篡改性、去中心化等特性，使得区块链成为一个适合密封式电子拍卖的平台。基于区块链的密封式投标拍卖可以有效去除第三方，从而节省第三方拍卖中心的费用。拍卖活动的稳定进行依赖于拍卖系统的安全性和稳定性，区块链上的数据不可篡改性并且可追溯，一旦交易确认，无法修改历史记录，保证投标后拍卖报价就不可修改和撤销。区块链上地址的匿名性也可以保证竞买人的身份隐私。目前已有一些研究通过区块链来实现密封式投标拍卖。如Galal 等［10］提出了一个智能合约，用于以太坊区块链上的可验证密封竞价拍卖方案，协议确保了拍卖结果公开的可验证性、投标的保密性和公平性。Galal 等［11］又提出了一种在以太坊区块链上基于简洁非交互式零知识证明zk-SNARKs（zeroknowledge Succinct Non-interactive ARgument of Knowledge）的拍卖方案，通过拍卖人和竞买人之间的多方安全计算协议生成zk-SNARKs 的证明和验证密钥，该方案可以解决竞买人与拍卖行间的信任问题。彭烨等［12］提出了一种基于区块链和并发签名的密封式投标拍卖方案，利用并发签名的模糊性保护竞标者的信息不被泄露，同时保证标价的保密性和竞标者的匿名性和不可否认性。Xiong 等［13］介绍了基于联盟链的密封竞标拍卖协议，利用数字证书的身份机制和基于椭圆曲线技术的盲签名来允许竞标者匿名参与，并采用定时释放公钥加密算法对竞拍进行加密，防止拍卖人与竞拍人串通。

本文针对目前竞拍系统中的隐私泄露、不可公开验证等缺陷，提出了一种基于区块链的密封式投标拍卖方案。通过区块链上的安全保证金策略约束竞买人行为，利用Pedersen承诺方案保护竞买人的信息不被泄露，利用同态加密的加法同态性进行密文的算术运算，竞买人可以利用零知识范围证明来验证中标价格的正确性。

1 预备知识

1.1 区块链

2008 年中本聪在《比特币：一种点对点电子现金系统》［14］一文中首次提出区块链的概念。区块链本质上是一种多方参与共同维护的分布式数据库，采用对等网络（Peer-to-Peer，P2P）的网络通信方式，通过密码学技术保护隐私，利用智能合约［15］实现业务逻辑，依赖分布式共识技术实现存储一致。与传统的数据结构不同，区块链采用链式结构存储，将数据记录组织成区块（Block），并在每个区块的区块头中通过记录前一区块的哈希值将区块组织成链式结构。

区块链在走向应用之前，必须解决隐私问题。在区块链中主要保护两类隐私：身份隐私和交易隐私［16-17］。保护身份隐私是指减少用户身份与区块链地址之间的关联。在区块链上用户可以创建多个地址，与用户的身份无关，并且创建过程不需要第三方参与。因此通过地址信息很难将用户身份关联起来，相较于传统创建的地址信息来说具有较好的匿名性。保护交易隐私是指保护在区块链中存储的交易记录和交易隐藏的信息（如交易金额、用户的消费水平等）。目前区块链主要采用隐蔽地址［18］、同态加密［19］、零知识证明［20］等方案保护隐私。

1.2 承诺方案

在机密交易中，可以用Pedersen 承诺算法［21］保护交易金额的隐私性。该承诺算法由承诺者向接收者承诺某个秘密数，即生成某个承诺值。接下来通过展示该秘密数，由接收者确认前后承诺值是否相等。基于椭圆曲线的Pedersen 承诺算法表现形式如下：

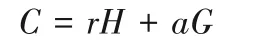
其中：C为椭圆曲线上的一个曲线点，作为承诺值；a为需要承诺的秘密数；r为随机数值；G为所选择椭圆曲线上的生成元；H为椭圆曲线上的另一个基点。

基于椭圆曲线问题的难解性，该承诺方案是抗冲突的并且不会泄露被承诺的信息，因此具有隐藏性和绑定性；而且该承诺方案满足加法同态性，即：

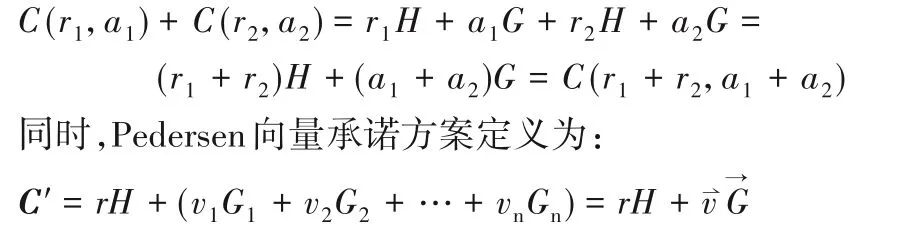
1.3 零知识证明Bulletproofs

零知识证明是指证明者能够在不向验证者提供任何有用信息的情况下，使验证者相信某个论断是正确的。Bulletproofs［22］是一种新的非交互式零知识证明协议，具有证明时间短、不需要可信设置的特点。从计算要求上看，该证明系统的性能优于zk-SNARKs［23］和zk-STARKs（zero-knowledge Succinct Transparent ARgument of Knowledge）［24］，且在加密货币系统中具有实用性。Bulletproofs 可以证明交易的金额在给定的正区间内，这对验证交易至关重要。它依赖于Pedersen承诺来隐藏秘密输入并提供计算完整性检查。

具体过程如下：

2 竞拍方案

在本章中描述了基于区块链的密封式投标拍卖方案的具体流程。在竞拍流程中利用Pedersen 承诺方案保护竞买人的信息不被泄露，将零知识范围证明与承诺机制结合，可以在不泄露中标者身份信息的情况下进行验证，保证中标者身份不可伪造和中标价格的正确性，在不泄露隐私的情况下，能够高效地完成竞拍任务。

2.1 竞拍流程

拍卖方案总共分为拍卖准备阶段、任务发布阶段、竞标阶段、公开中标者承诺阶段、证明阶段、验证阶段和拍卖完成阶段。该方案包含三个实体：拍卖者、竞买人和拍卖合约。拍卖者需要将想要拍卖的物品信息这个任务发布到区块链中，因区块链具有产生新数据块的属性，待区块链产生新块时，这个任务发布成功。在身份注册成功后，竞买人可以查看区块链中已有的拍卖任务，对感兴趣的任务进行竞价。为了保证竞拍有意义，拍卖合约将进行相应的计算，判断最低竞价的数量，在竞买人数量大于等于2 时，竞拍任务继续进行。接下来，各个竞买人提交报价承诺，最终由拍卖人公布中标者的承诺值。其余竞买人将会验证收到的证明记录，验证通过后可以结束拍卖。拍卖服务整体流程如图1所示。

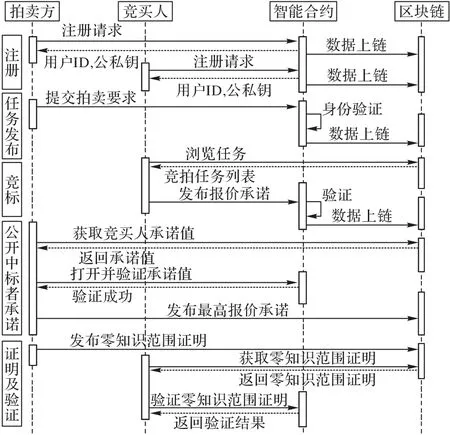
图1 拍卖服务流程Fig.1 Flowchart of auction service

2.2 竞拍阶段

2.2.1 符号介绍

2.2.2 拍卖准备阶段

拍卖方案包含三个实体：拍卖者、竞买人、拍卖合约。各个参与方在使用拍卖合约之前，竞买人和拍卖者必须进行注册成为合法用户才能参与拍卖。注册成功后用户持有一对公钥、私钥和一个身份ID，身份ID 将以哈希值Hash（ID）的形式存储在区块链中。

算法1 拍卖准备阶段算法。

2.2.3 任务发布阶段

拍卖者使用智能合约账户的公钥对身份ID 进行加密得到E(H(Uid))；

拍卖方利用智能合约初始化拍卖状态，并提交拍卖要求。

智能合约根据其私钥进行解密得到竞买人的身份信息H(Uid)′并判断等式H(Uid)=H(Uid)′是否成立，如若成立，则身份验证成功；否则，丢弃该拍卖任务。

算法2 任务发布阶段算法。

2.2.4 竞标环节

首先竞买人Pi需要完成和拍卖方相同的身份认证，仅当通过身份认证的竞买人才能参加竞拍活动。Pi浏览已经发布在区块链中的任务，在提交承诺截止时间T3之前，对自己感兴趣的任务进行投标，即在区块链中发布自己的报价承诺：Ci=xiG+riH，每个竞买人Pi将xi、ri通过拍卖方的公钥加密后发送到区块链上。

智能合约在判定当前时间T小于T3后，判断在竞买人Pi有足够余额的情况下，从Pi账户扣除保证金，转入到合约的保证金账户中。随后将竞买人Pi加入到竞买人集合中，并将竞买人的报价承诺存储在区块链上。完成执行上述操作后，Pi投标成功。为了保证此次拍卖活动有意义，智能合约会判断投标人数num，仅当拍卖活动num≥2时，拍卖可继续进行。

算法3 竞标环节算法。

2.2.5 公开中标者承诺阶段

拍卖方在T2时利用私钥得到xi'、ri'，重新计算出承诺值C'，判断C=C′，若相等则认为竞买者诚实的在区块链上发布承诺值。拍卖方选择最高报价W作为中标价。拍卖方公布中标者承诺CW，而不公布中标者的真实报价。

算法4 公开中标者承诺阶段算法。

2.2.6 证明阶段

假设失败的竞买人报价为L，承诺为CL，则d=W-L，Cd=CW-CL。如果W＞L，则d＞0。拍卖方打开承诺后，计算出差价d，根据Pedersen 承诺计算出Cd，发送给每一个竞买人。

算法5 证明阶段算法。

2.2.7 验证阶段

其余竞买人作为一个独立的验证者，首先根据中标者的公开承诺和自己的承诺计算，用Cd来确保他们收到正确的证明记录。竞买人利用Cd'=CW-CL，比较Cd是否等于Cd'。若相等，则其余失败竞买人可以确认拍卖方发送给他们的承诺值Cd是正确的。

拍卖方设置零知识范围证明，证明d位于范围[0，2n-1]且不会被泄露，n表示可能的最大出价的位大小，任何出价之间的最大可能差为[-(2n-1)，2n-1]。若L＞W，则d＜0 且群大小p足够大，则负值d将位于范围间隔之外。拍卖者向每个验证者发送一份范围证明记录，该记录使验证者使用协议来验证以下关系：

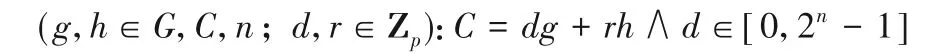
失败的竞买人通过验证出d的范围从而得知中标价为最高价。

算法6 验证阶段算法。

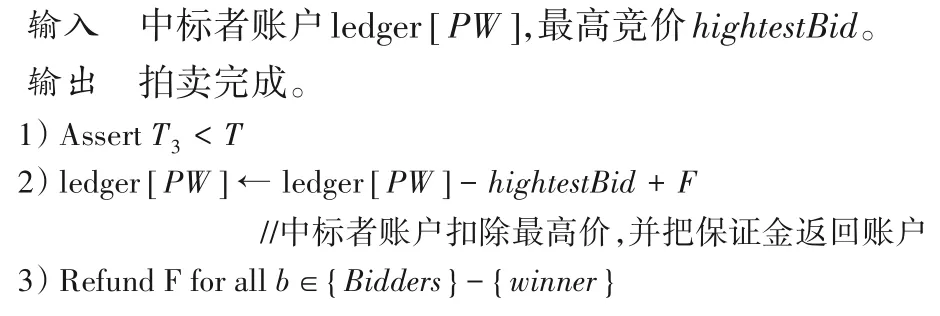
2.2.8 拍卖完成阶段

智能合约在该阶段将所有未中标的诚实参与者的保证金返回其账户，中标者则需支付中标与初始保证金F之间的差额。

算法7 拍卖完成阶段算法。

3 方案分析

3.1 安全性分析

本文的拍卖方案基于区块链技术，利用承诺值的区间验证来保护数据隐私，而不泄露任何隐私信息，相较于传统的中心化存储具有明显优势：去中心化的存储降低了黑客攻击的风险，也避免了单一节点失效带来的系统数据丢失的隐患。本文拍卖方案能有效满足电子拍卖的需求：

1）正确性。拍卖人在公开中标者承诺阶段选择最高价作为中标者，保障拍卖的正确性。

2）公平性。区块链上所有用户权利相等，区块链上数据公开透明，所有用户获得信息一致。由于拍卖方发起拍卖后需要交纳竞价保证金F。假设拍卖方不诚实，此时拍卖方既拿不到竞价保证金，也无法使拍卖成功进行。

3）密封性。对于拍卖人A、竞拍方Pi，在时间T2前对其可见的信息只有承诺值、公钥加密后的密文。竞买人Pi承诺值的(xi，ri)用拍卖者公钥Pi加密后发送到智能合约账户上，对于拍卖人A，在时间T2前对其可见的信息只有承诺值，所以拍卖人A不能将竞买人的(xi，ri)发送给其他竞买人，从而避免Pi的承诺值被模仿。

4）不可否认性。区块链所具有的不可篡改性，中标者W在竞标成功后不可以对自己的出价进行否认。

5）可验证性。未中标用户可以通过零知识证明协议验证证明阶段收到的范围证明的正确性，保证中标价为最高价。

6）时限性。利用智能合约自动触发的特点，竞拍承诺提交后只有在T2时间段才能打开。

7）不可伪造性。拍卖方案开始和最终都有一个身份验证过程，任何人不能用伪造的身份参与竞拍活动。并且假设拍卖人A对竞买人Pi是恶意的，声明竞买人Pi发送在智能合约上的密文是无效的。此时诚实的竞买人可以在拍卖合约上发出(xi，ri)，拍卖合约通过公钥Pk加密的值如果发现密文与之前提交的密文相等，将对拍卖人进行处罚，并将保证金退还给Pi，该惩罚由智能合约执行。

3.2 实验结果分析

本文使用如表1所示的测试环境进行测试。

通过表2 可看出，竞拍各个阶段运行时间在毫秒以内，运行花费时间在可接受范围内，基本不会对日常应用造成影响。

表1 实验环境Tab.1 Experimental environment

表2 不同阶段的运行时间 单位：msTab.2 Running times of different stages unit：ms

本文竞拍方案与其他方案的对比如表3所示。

表3 方案对比Tab.3 Scheme comparison

基于fabric 对本文方案进行设计实现，实验如图2 所示生成了一份报价承诺，图3 展示了生成的零知识范围证明，图4对生成的证明验证，并验证成功。实验结果表明本文方案是可行的。

图2 生成报价承诺Fig.2 Generating quotation commitment

图3 生成范围证明Fig.3 Generating range proof

图4 验证收到承诺Fig.4 Verifying commitment received

本文设计了基于区块链的密封式投标拍卖方案。相较于传统密封式投标拍卖，充分地利用区块链不可篡改、去中心化等特性，有效去除第三方，避免了单点故障和操作的不透明。彭烨等［12］提出的方案所选出的中标价是否的确高于其余竞拍价的正确性不可验证；而本文方案可以验证中标价的正确性。程文娟等［8］提出的方案满足匿名性、保密性和不可伪造性，但其不能公开验证成交价，而是由拍卖中心计算和公布。对比而言，本文方案是由拍卖方公布中标者的承诺，而不公布除承诺以外的信息，利用区块链保证公布信息的真实性。

4 结语

本文提出的基于区块链的密封式投标拍卖方案，在不泄露隐私的情况下，能够高效地完成竞拍任务。本文方案将零知识范围证明与承诺机制结合，可以在不泄露中标者身份信息的情况下进行验证，并通过数字货币保证金来提高拍卖的公平性和约束竞买人的行为。同时，借助于区块链去中心化、不可篡改等特性，有效地去除第三方，避免了单点故障和操作的不透明性，实现了密封式电子拍卖协议要求的正确性、公平性、密封性、不可否认性、时限性以及中标者的公开可验证性。