半导体温差发电转换效率研究

2021-04-20冯倩倩杨浩钦韩娅钟

无线互联科技 2021年4期

冯倩倩，杨浩钦，韩娅钟，冷敏，肖啸

（乐山师范学院数理学院，四川乐山 614000）

0 引言

半导体温差发电利用了塞贝克效应（Seebeck Effect）直接将热能转换为电能，在发电时无须先将热能转化为机械能再由机械能转化为电能的间接转换过程，整个发电装置没有活动的机械部分，只要半导体PN结两端存在温度差就能输出电能，具有无噪音、维护成本低、长寿命等优点，逐渐受到人们的重视[1-5]。通过选择合适的半导体材料种类，半导体温差发电单元可以在很宽的温度范围内（300K～1 400K）实现热能到电能的直接转换。但由不同半导体材料和装置结构组成的温差发电组件，在相同的温差场条件下，发电组件的输出功率、输出电压、输出电流、稳定性等组件性能参数都存在着较大差异。因此，优化半导体温差发电组件，提高温差发电组件热电转换效率，探究如何发挥热电组件性能有着重要的现实意义[3-5]。本文将以半导体温差发电原理为基础，从理论上推导温差发电效率公式并分析其影响因素，最后进行实验探究与验证。

1 半导体温差发电原理

塞贝克效应的实质在于两种金属或半导体材料接触时产生了接触电势差，半导体的接触电势差远大于金属导体，因此温差发电的电动势单元一般采用半导体材料制成。如图1所示，半导体单元从温度为高温热源处吸热，其中部分热量转换为电能向负载输出，另一部分热量向温度为低温热源排放。在此过程中产生的温差电动势可由（1）式确定。

其中αp,n为由半导体材料性质所决定的相对塞贝克系数。高温端的吸热和低温端的放热可由（2）式描述[3]。

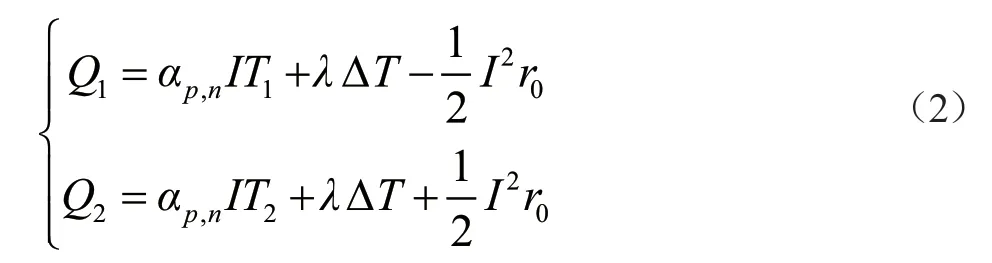
其中ΔT=T1－T2,是高低温热源温度差,λ为材料的热导率，r0为发电单元内阻。

图1 半导体温差发电示意图

2 半导体温差发电效率分析

温差发电效率可由输出功率和高温热源吸热之比值定义。若输出负载等效电阻为R，其输出功率为I2R，则温差发电效率为：

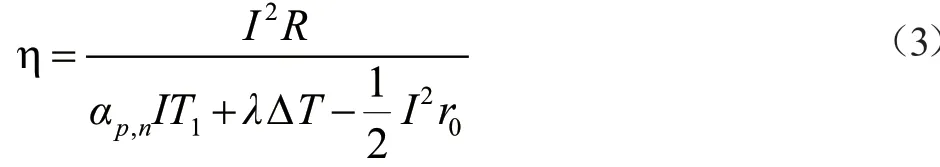
定义匹配系数m=R/r0，优质系数则可将上式改写为：

由于优质系数Z与半导体温差发电片本身性质有关，在此仅分析温差ΔT和匹配系数m对发电效率的影响。图2显示了m和ΔT对发电效率的影响关系曲线，从中可看出，对于同一m值，发电效率随着ΔT的增加而提高；而当ΔT固定时，效率的最大值出现在匹配系数为1.2～1.4之间。图3显示了最佳匹配条件下效率随ΔT的变化关系，从中可看出，在分析温度范围内，二者之间呈现线性关系，同时还可看出在同一ΔT时，效率随T1的增加而减小。

图2 m和ΔT对效率的影响

3 验证与分析

由前面的理论推导与分析可知，提高温差ΔT和优化匹配系数m均能提高半导体的温差发电效率。为验证上述分析结果，本文设计了不同的实验方案，因篇幅限制，文中仅选取部分方案进行分析。

图3 最优匹配条件下ΔT对效率的影响

为增加温差ΔT，可采用的措施有提高高温热源温度T1和降低低温热源温度T2。在外界热源固定的情况下，可以通过改变吸热和散热结构的方法增大T1和降低T2，比如增大吸、散热结构的面积和形状，改变吸、散热结构的材质等等。表1显示了在吸热结构不变的情况下，采用不同的散热结构降低低温热源T2从而增大ΔT，从表中可以看出插片式散热结构具有更高的效率，其原因在于该结构能获得更好的散热效果。

在固定吸、散热结构形状不变情况下，采用铜和铝作为吸、散热材料，实验结果显示采用铜结构的温差发电单元具有更高的发电效率，这是因为铜具有更好的热传导系数。

保持半导体温差发电单元不变，改变负载电阻从而获得不同的匹配系数，实验结果如表2所示，由表中数据可知，实验数据变化趋势与前面的理论分析一致。