Iterative Methods for Solving the Nonlinear Balance Equation with Optimal Truncation
2021-04-20QinXUandJieCAO
Qin XU and Jie CAO
1NOAA/National Severe Storms Laboratory, Norman, Oklahoma 73069, USA
2Cooperative Institute for Mesoscale Meteorological Studies, University of Oklahoma, Norman, Oklahoma 73072, USA
3Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
(Received 27 August 2020; revised 16 November 2020; accepted 20 December 2020)
ABSTRACT Two types of existing iterative methods for solving the nonlinear balance equation (NBE) are revisited. In the first type, the NBE is rearranged into a linearized equation for a presumably small correction to the initial guess or the subsequent updated solution. In the second type, the NBE is rearranged into a quadratic form of the absolute vorticity with the positive root of this quadratic form used in the form of a Poisson equation to solve NBE iteratively. The two methods are rederived by expanding the solution asymptotically upon a small Rossby number, and a criterion for optimally truncating the asymptotic expansion is proposed to obtain the super-asymptotic approximation of the solution. For each rederived method, two iterative procedures are designed using the integral-form Poisson solver versus the over-relaxation scheme to solve the boundary value problem in each iteration. Upon testing with analytically formulated wavering jet flows on the synoptic, sub-synoptic and meso-α scales, the iterative procedure designed for the first method with the Poisson solver, named M1a, is found to be the most accurate and efficient. For the synoptic wavering jet flow in which the NBE is entirely elliptic, M1a is extremely accurate. For the sub-synoptic wavering jet flow in which the NBE is mostly elliptic,M1a is sufficiently accurate. For the meso-α wavering jet flow in which the NBE is partially hyperbolic so its boundary value problem becomes seriously ill-posed, M1a can effectively reduce the solution error for the cyclonically curved part of the wavering jet flow, but not for the anti-cyclonically curved part.
Key words: nonlinear balance, iterative method, optimal truncation
1. Introduction
For flows of synoptic and sub-synoptic scales in the middle and high latitudes, the nonlinear balance equation(NBE) links the streamfunction field with the geopotential field more accurately than the geostrophic balance (Bolin,1955; Charney, 1955). However, solving the streamfunction from the NBE for a given geopotential field can be very challenging due to complicated issues on the existence of solution in conjunction with difficulties caused by nonlinearity(Courant and Hilbert, 1962). It is well known mathematically that the NBE is a special case of the Monge-Ampere differential equation for the streamfunction (Charney, 1955). If the geostrophic vorticity (that is, the vorticiy of geostrophic flow associated with the given geopotential field) is larger than −f/2 for a constant f where f is the Coriolis parameter,then the NBE is of the elliptic type and its associated boundary value problem can have no more than two solutions (see Section 6.3 in Chapter 4 of Courant and Hilbert, 1962). If the geostrophic vorticity is smaller than −f/2 in a local area,then the NBE becomes locally hyperbolic. In this case, the boundary value problem becomes ill-posed and thus may have no solution although the NBE can be integrated along the characteristic lines within the locally hyperbolic area(see Section 3 of Appendix I in Chapter 5 of Courant and Hilbert, 1962).
To avoid the complication and difficulties caused by the local non-ellipticity in solving the NBE, one can simply enforce the ellipticity condition to a certain extent by slightly smoothing or adjusting the given geopotential field.This type of treatment has been commonly used in iterative methods to solve the NBE as a boundary value problem(Bolin, 1955, 1956; Shuman, 1955, 1957; Bushby and Huckle, 1956; Miyakoda, 1956; Arnason, 1958; Bring and Charasch, 1958; Liao and Chow, 1962; Asselin, 1967;Bijlsma and Hoogendoorn, 1983). However, regardless of the above treatment, the convergence properties of these or any other iterative methods can be not only scale-dependent but also flow-dependent and thus very difficult to study theoretically and rigorously.
The above reviewed iterative methods can be classified into two types. In the first type (originally proposed by Bolin, 1955), the NBE is transformed into a linearized equation for a presumably small correction to the initial guess or to the subsequent updated solution when this linearized equation is solved iteratively. In the second type (originally proposed by Shuman, 1955, 1957; Miyakoda, 1956), the NBE is rearranged into a quadratic form of the absolute vorticity and the positive root of this quadratic form is used in the form of a Poisson equation to solve for the streamfunction iteratively. The initial guess for both types is the geostrophic streamfunction. Their convergence properties have been analyzed theoretically, but the analysis lacks rigor and generality, because the coefficients of the linearized differential operator for the first type and the forcing terms on the right-hand side of the iterative form of the linearized equation for the second type were functions of space but treated as constants (Arnason, 1958; Bijlsma and Hoogendoorn,1983). Therefore, the convergence properties of the previously iterative methods were examined mainly through numerical experiments. Besides, due to the very limited computer memories and speed at that time, these earlier iterative methods employed the memory-saving sequential relaxation scheme based on the classical Liebmann-type iteration algorithm (Southwell, 1946) and applied to coarse resolution grids for large-scale flows. The sequential relaxation and successive over-relaxation (SOR) schemes have been used in the second type of iterative method (Shuman, 1955,1957) to solve the NBE for hurricane flows (Zhu et al.,2002). However, using these iterative methods to solve the NBE still faces various difficulties especially when the spatial scale is smaller than the sub-synoptic scale. In particular, there are unaddressed challenging issues concerning whether and how the solutions can be obtained approximately and efficiently through a limited numbers of iterations,especially when the NBE becomes locally hyperbolic (due mainly to reduced spatial scales) and thus the iterative methods fail to converge.
This paper aims to address the above challenging issues. In particular, we will rederive the above two types of iterative methods formally and systematically by expanding the solution asymptotically upon a small Rossby number and substituting it into the NBE. Since the asymptotic expansion is not ensured to converge, especially when the Rossby number is not sufficiently small, the concept of optimal truncation of asymptotic expansion is employed and a criterion is proposed to obtain the super-asymptotic approximation of the solution based on the heuristic theory of asymptotic analysis (Boyd, 1999). As will be seen in this paper, by employing the optimal truncation, the issue of non-convergence of the iterative methods caused by the increase of Rossby number can be addressed to a certain extent. Besides, the recently developed Poisson solver based on integral formulas (Cao and Xu, 2011; Xu et al., 2011) will be used in comparison with the aforementioned classical SOR scheme to solve the boundary value problem in each iterative step. In particular, for flows of sub-synoptic scale or meso-α
scale,the NBE can become locally hyperbolic and the solution will be checked in this paper via the proposed optimal truncation under certain conditions.The paper is organized as follows. The next section presents formal and systematical derivations of the above reviewed two iterative methods. Section 2 formulates the criterion for optimal truncation, and section 3 constructs four different iterative procedures with optimal truncation and designs numerical experiments for testing the iterative procedures. Section 4 examines and compares the results of experiments performed with the four iterative procedures, followed by conclusions in section 5.
2. Derivations of two iterative methods
2.1. Scaling and asymptotic expansion based on small Rossby number
The NBE can be expressed in the following form (Charney, 1955):

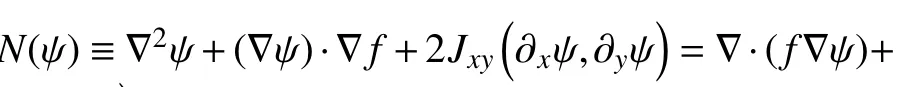
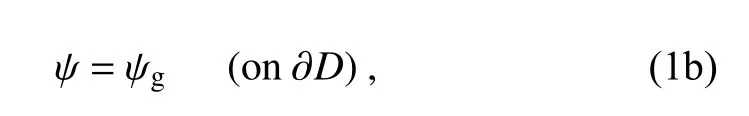
D
denotes the domain boundary, and ψ≡ϕ/f
is the global geostrophic streamfunction (Kuo, 1959; Charney and Stern, 1962; Schubert et al., 2009).Formally, we can scale x and y by L, scale f = f+ f′
by f, and scaleψ
andϕ
by UL and fUL, respectively, where U is the horizontal velocity scale, L is the horizontal length scale, fis a constant reference value of f which can be the value of f at the domain center. The scaled variables are still denoted by their respectively original symbols, so the NBE can have the following non-dimensional form:
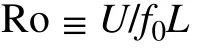
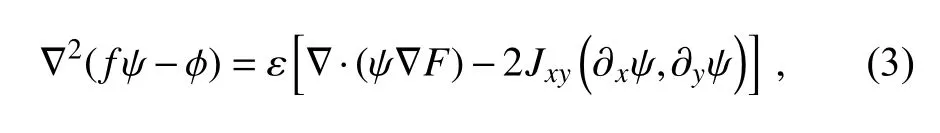
′
/(fRo) ≤ O(1) and O() is the “order-of-magnitude” symbol. Thus,ψ
can have the following asymptotic expansion: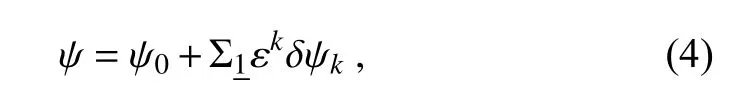
ψ
=ψ
and Σdenotes the summation over k from 1 to ∞. The kth order truncation of the asymptotic expansion ofψ
in Eq. (4) is given by ψ≡ψ+Σεδψ′ , where Σdenotes the summation over k' from 1 to k. Formally,ψ
=ψ
+O(ε
), soψ
is accurate up to O(ε
) as an approximation ofψ
.By substituting Eq. (4) into Eq. (3) and Eq. (1b), and then collecting terms of the same order ofε
, we obtain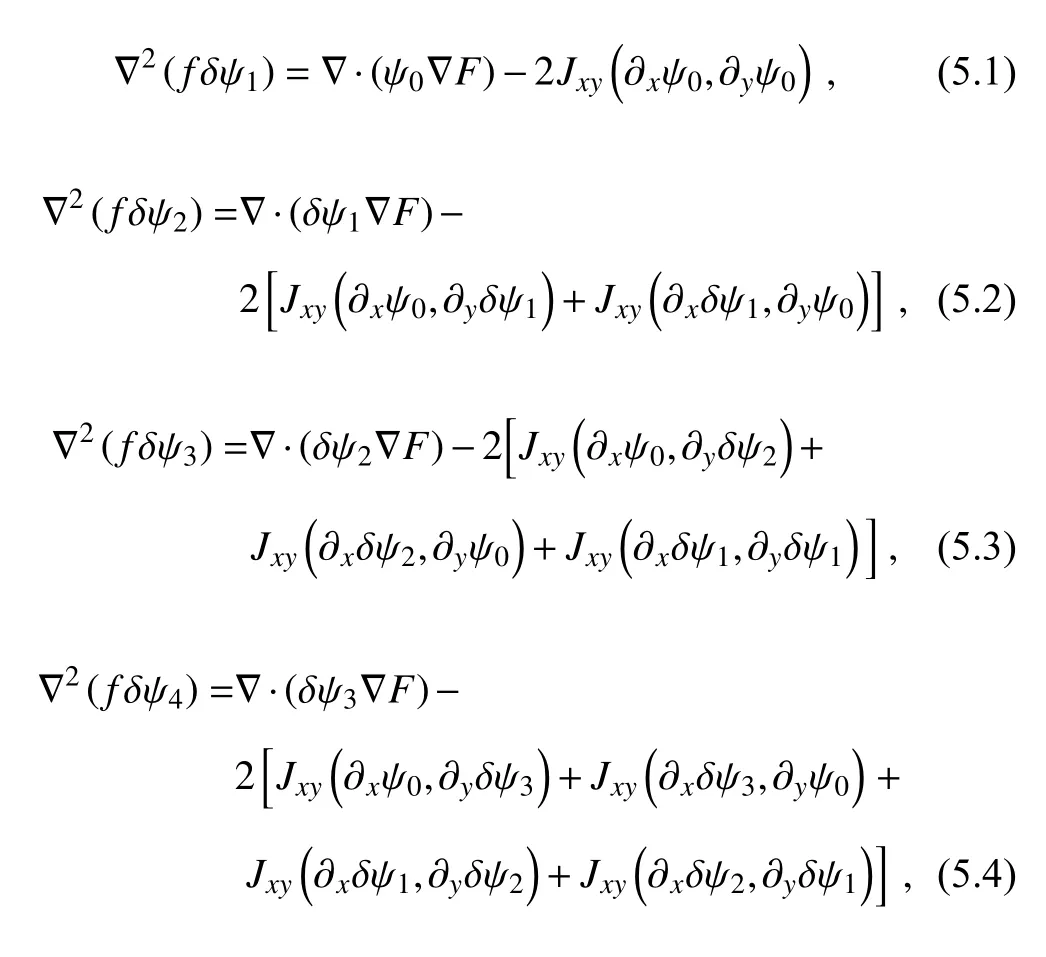
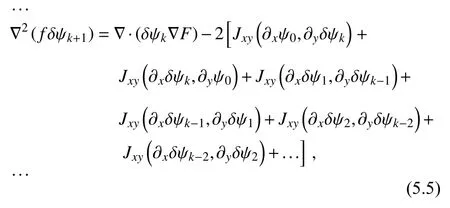
δψ
consecutively fromδψ
to increasingly higher-order term in the expansion ofψ
with the boundary conditions ofδψ
= 0 (on ∂D
for k = 1, 2, 3, …). The equations in Eq. (5), however, are inconvenient to use, because the equation at each given order becomes increasingly complex as the order k increases. It is thus desirable to modify Eq. (5) into a recursive form, and this can be done nonuniquely by first combining the equations in Eq. (5) with∇( fψ
) = ∇ϕ
into a series of equations forψ
(instead ofδψ
) and then adding properly selected higher-order terms to the equation forψ
at each order without affecting the order of accuracy of the equation. In particular, two different modifications will be made in the next two subsections.From these two modifications, the two types of iterative methods reviewed in the introduction for solving the NBE can be derived formally and systematically via the asymptotic expansion ofψ
in Eq. (4).2.2. Derivation of method-1
The equations in Eq. (5) can be combined with ∇(fψ
) =∇ϕ
at O(ε
) into a series of equations forψ
defined in Eq.(4) as shown blow: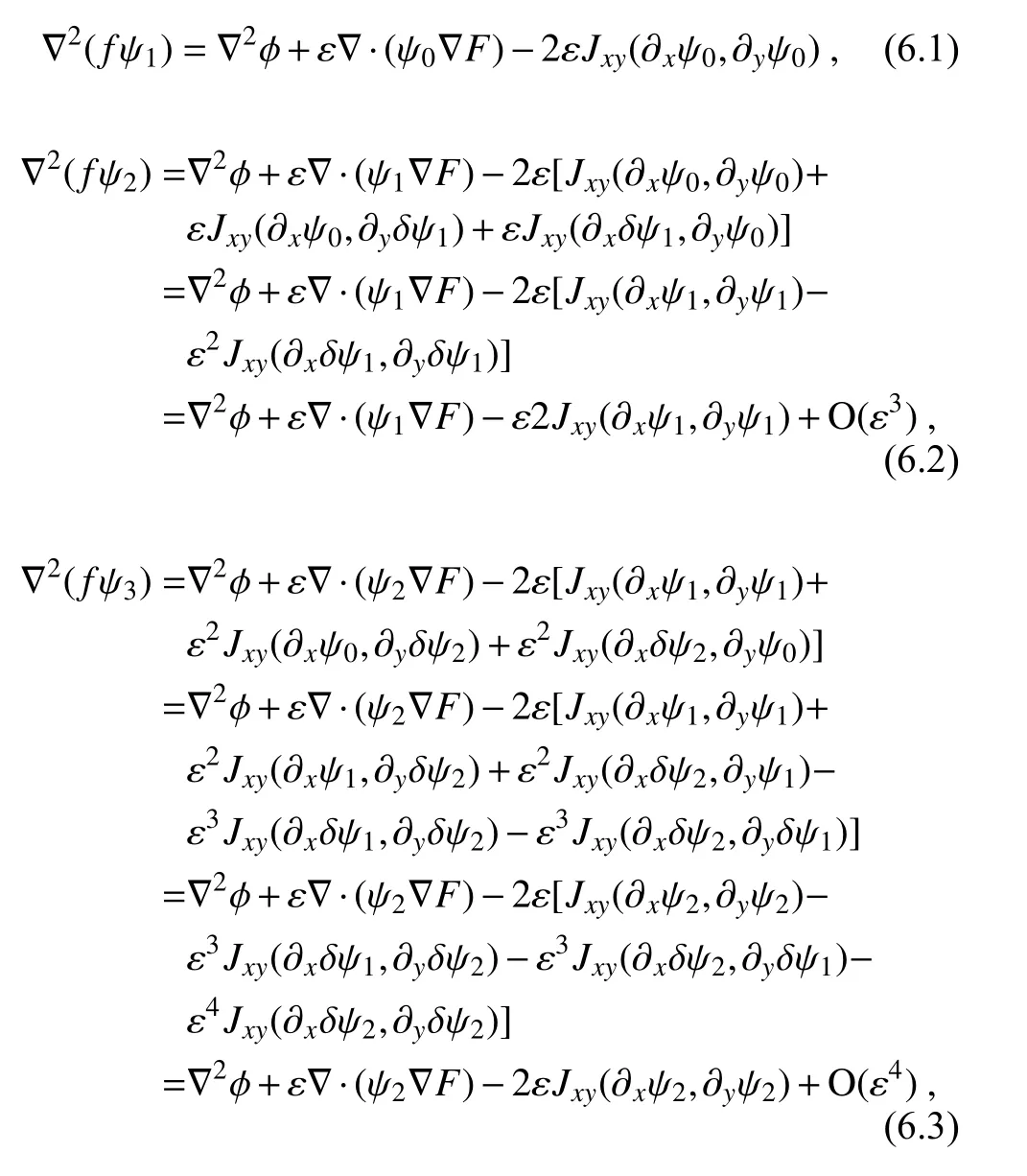

ψ
is accurate up to O(ε
) and so is ∇(fψ
) on the left-hand side of the above kequation. This implies that the kequation is accurate only up to O(ε
), so the last term O(ε
) (that represents all the high-order terms) on the right-hand side can be neglected without degrading the order of accuracy of the equation. This leads to the following recursive form of equation and boundary condition for solving the NBE iteratively: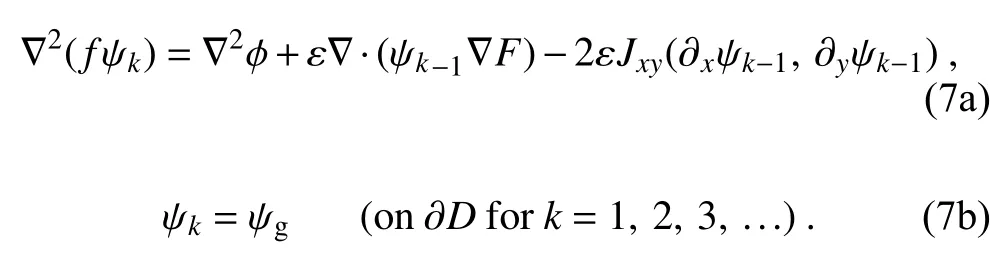
ε
is sufficiently small to ensure the convergence of the asymptotic expansion in Eq. (4), thenψ
→ψ
gives the solution of the NBE in the limit of k → ∞.Substituting ε∇F
=∇f
/f
andε
= Ro ≡ U/fL into Eq.(7) gives the dimensional form of Eq. (7):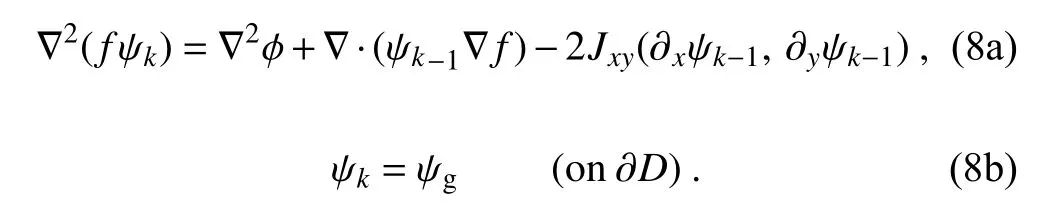
ψ
=ψ
+ε
δψ
, that is,ψ
=ψ
+δψ
into Eq. (8) gives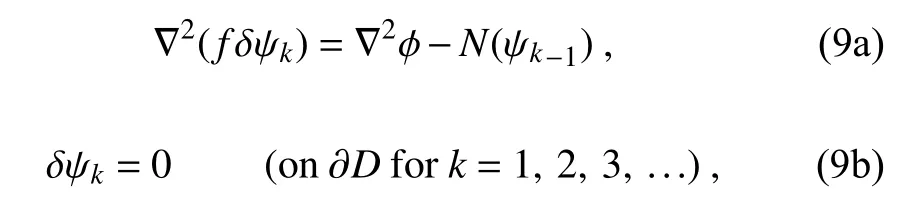
δψ
from Eq. (9) and updatingψ
toψ
=ψ
+δψ
iteratively does not give exactly the same solution as that obtained by solvingψ
from Eq. (8) iteratively. According to our additional numerical experiments (not shown),the solutions obtained from Eq. (8) are less accurate (by about an order of magnitude for the case of Ro = 0.1) than their counterpart solutions obtained from Eq. (9), so the non-incremental form of boundary value problem in Eq. (8)will not be considered in this paper.2.3. Derivation of method-2
The equation forψ
in Eq. (6.4) can be multiplied by 2 and rewritten as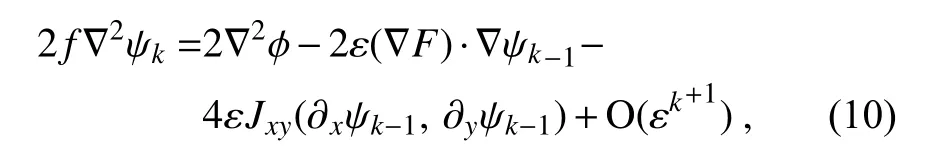
ψ
=ψ
+ε
δψ
=ψ
+ O(ε
) and ∇(fψ
) = fζ
+( ∇f)·∇
ψ
+ ∇·(ψ
∇ f ) = fζ
+ε
( ∇F)·∇
ψ
+ε
∇·(ψ
∇ F) = fζ
+ε
( ∇F)·(∇
ψ
) +ε
∇· (ψ
∇ F) + O(ε
) are used. One can verify that −4ε
J(∂ψ, ∂ψ) =ε
(ζ
− A− B) =εζ
−ε
(A+ B) + O(ε
) whereζ
= ∇ψ
, A≡(∂−∂)ψ
, B≡ 2∂∂ψ, and A= (∂−∂)(ψ
+ε
δψ
) = A+ O(ε
) and B= 2 ∂∂(ψ
+ε
δψ
) = B+O(ε
) are used. Substituting these into Eq. (10) gives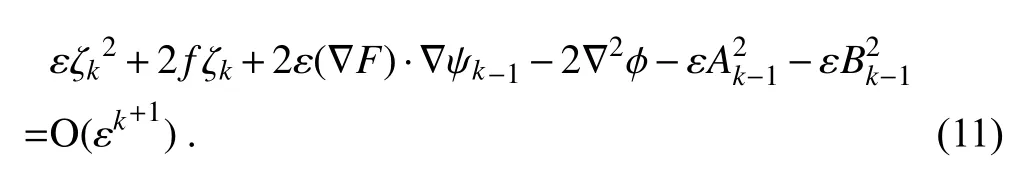
ε
):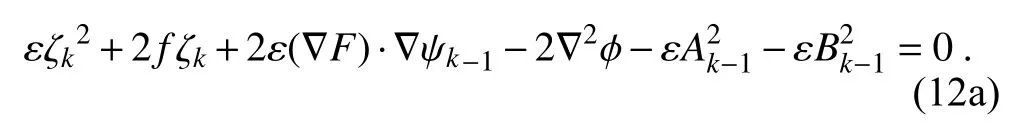
F
=∇f
/f
andε
= Ro ≡ U/(fL) into Eq.(12a) gives its dimensional form which can be rewritten as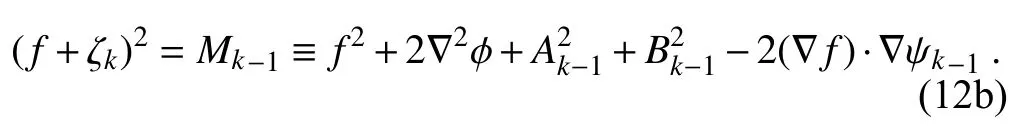
ζ
)≥ 0 requires M≥ 0 on the right-hand side of Eq. (12b). Also, as a quadratic equation of f +ζ
for givenϕ
andψ
, Eq. (12b) has two roots, but only the positive root, given by f +ζ
=M, is physically acceptable (because f +ζ
≥ 0 is required for stably balanced flow). This leads to the following recursive form of equation and boundary condition for solving the NBE iteratively:
where M≥ 0 is ensured by setting M= 0 when the computed Mfrom the previous step becomes negative. Here,Eq. (13a) gives essentially the same recursive form of equation as that in Eq. (8) of Shuman (1957) for solving the NBE iteratively, but this recursive form of equation is derived here via the asymptotic expansion of the solution in Eq. (4).
3. Iterative procedures with optimal truncation and experiment design
3.1. Criterion for optimal truncation
When the Rossby number is not sufficiently small to ensure the convergence of the asymptotic expansion, the optimal truncation of the asymptotic expansion ofψ
in Eq.(4) can be determined (Boyd, 1999) by an empirical criterion in the following dimensional form: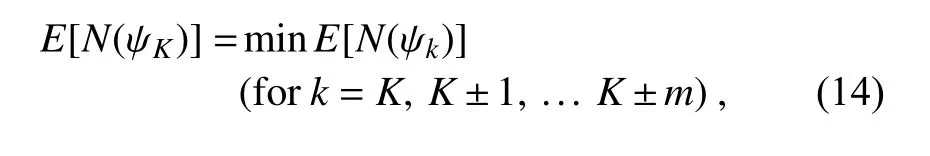
ψ
)] ≡ ||ε
[N(ψ
)]||′, || ||′denotes the root-mean-square (RMS) of discretized field of the variable inside || ||′ computed over all the interior grid points (excluding the boundary points) of domain D, andε
[N(ψ
)] ≡ [N(ψ
) − N(ψ
)]/||N(ψ
)||′ = [N(ψ
) − ∇ϕ
]/||∇
ϕ
||′is the relative error of N(ψ
) with respect to N(ψ
) which is also the normalized (by ||∇
ϕ
||′) residual error of the NBE caused by the approximation ofψ
≈ψ
, andψ
denotes the true solution. Here, E[N(ψ
)] is expected to be the global minimum of E[N(ψ
)]. If E[N(ψ
)] does not oscillate as k increases, then it is sufficient to set m = 1 in Eq. (14). Otherwise, m should be sufficiently large to ensure E[N(ψ
)] be the global minimum of E[N(ψ
)].3.2. Iterative procedures
The iterative procedure for method-1 performs the following steps:
1. Start from k = 0 and setψ
=ψ
≡ϕ
/f in D and ∂D
.2. Substituteψ
(=ψ
for k = 1) into N(ψ
) to compute the right-hand-side of Eq. (9a), and then solve the boundary value problem in Eq. (9) forδψ
.3. Substituteψ
=ψ
+αδψ
into ||N(ψ
) − ∇ϕ
||′ and save the computed ||N(ψ
) − ∇ϕ
||′ whereα
is an adjustable parameter in the range of 0 <α
≤ 1.4. If k ≥ 2m, then find min||N(ψ
) − ∇ϕ
||′, say at k′ =K′, for k′ = k, k − 1, … k − 2m. If K′ < k − m, then K = K′andψ
gives the optimally truncated solution–the final solution that ends the iteration. Otherwise, go back to step 2.When the Poisson solver (or SOR scheme) is used to solve the boundary value problem in the above step 2, the iterative procedure designed for method-1 is named M1a (or M1b). For the Poisson solver used in this paper, the internally induced solution is obtained by using the scheme S2 described in section 2.1 of Cao and Xu (2011) and the externally induced solution obtained by using the Cauchy integral method described in section 4.1 of Cao and Xu (2011). For M1a with Ro < 0.4 (or Ro = 0.4), it is sufficient to set m = 1 andα
= 1 (or 1/2). For M1b, it is sufficient to set m = 3 andα
= 1.The iterative procedure for method-2 performs the following steps:
1. Start from k = 0 and setψ
=ψ
≡ϕ
/f in D and ∂D
.2. Substituteψ
into Mdefined in Eq. (12b) to compute the right-hand-side of Eq. (13a), and then solve the boundary value problem in Eq. (13) forψ
.3. Compute and save ||N(ψ
) − ∇ϕ
||′.4. Perform this step as described above for step 4 of method-1.
When the Poisson solver (or SOR scheme) is used to solve boundary value problem in the above step 2, the iterative procedure designed for method-2 is named M2a (or M2b). For M2a and M2b, it is sufficient to set m = 1 andα
= 1.3.3. Experiment design
To examine and compare the accuracies and computational efficiencies of the four iterative procedures, the true streamfunction field is formulated for a wavering jet flow by
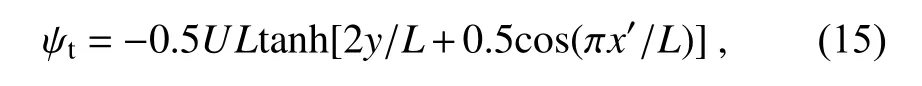
and the associated velocity components are given by
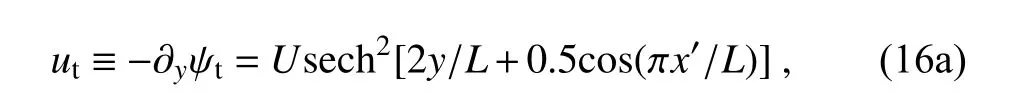
and
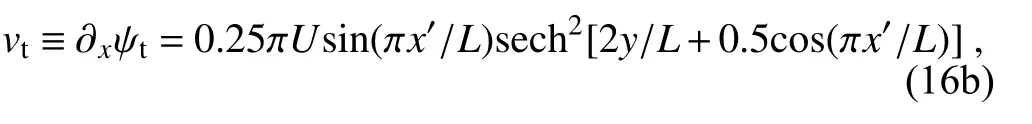
α
scales, respectively (as often observed on northernhemisphere mid-latitude 500 hPa weather maps).Four sets of experiments are designed to test and compare the iterative procedures withψ
given in Eq. (15) over a square domain of D ≡ [−L ≤ x ≤ L, −L ≤ y ≤ L]. The first set consists of four experiments to test the four iterative procedures (that is, M1a, M1b, M2a and M2b) on the synoptic scale by setting L = 2000 km and x= 0 forψ
in Eq. (15).The second set also consists of four experiments but to test the four iterative procedures on the sub-synoptic scale by setting L = 1000 km and x= 0 forψ
in Eq. (15). The third(or fourth) set still consists of four experiments to test the four iterative procedures on the meso-α
scale by setting L =500 km and x= 0 (or L) forψ
in Eq. (15). Note that setting x= 0 (or L) places the ridge (or trough) of the wavering jet in the middle of domain D, so the nonlinearly balanced flow used for the tests in the third (or fourth) set is curved anti-cyclonically (or cyclonically) in the middle of domain D. For simplicity, the Coriolis parameter f is assumed to be constant and set to f = f= 10sin all the experiments. The Rossby number, defined by Ro = U/fL, is thus 0.1, 0.2 and 0.4 for L = 2000, 1000 and 500 km, respectively.The true geopotential field,ϕ
, is obtained by solving the Poisson equation, ∇ϕ
= N(ψ
), numerically on a 51×51 grid over domain D with the boundary condition given byϕ
=fψ
. In this case,ψ
in Eq. (15) is also discretized on the same 51×51 grid over the same square domain, and is used to compute the right-hand side of ∇ϕ
= N(ψ
) via standard finite-differencing. Then,ϕ
is solved numerically by using the Poisson solver of Cao and Xu (2011). The SOR scheme can be also used to solve forϕ
, but the solution is generally less accurate than that obtained by using the Poisson solver.The NBE discretization error (scaled by ||∇
ϕ
||′) can be denoted and defined by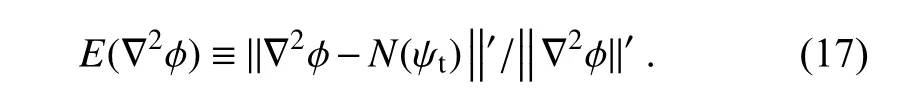
ϕ
obtained by using the Poisson solver with L = 2000 (or 1000) km but increases to 5.58×10(or 5.78×10) forϕ
obtained by using the SOR scheme. Thus, the solution obtained by using the Poisson solver is used as the input field ofϕ
in the NBE to test the iterative procedures in each set of experiments.4. Results of experiments
4.1. Results from first set of experiments
For this set of experiments,ψ
and (u, v) are plotted in Fig. 1a,ψ
and (u, v) ≡ (− ∂ψ, −∂ψ) are plotted in Fig.1b, the vorticityζ
≡ ∇ψ
is plotted in Fig. 1c, and the geostrophic vorticityζ
≡ ∇ψ
is plotted in Fig. 1d. Figure 1c shows that the absolute vorticity, defined by f +ζ
, is positive everywhere so the nonlinearly balanced wavering jet flow is inertially stable over the entire domain (see the proof in Appendix C of Xu, 1994). Figure 1c also shows that the geostrophic vorticityζ
is larger than −f/2 (= −f/2)everywhere, so the NBE is elliptic over the entire domain and its associated boundary value problem in Eq. (1) is well posed.The relative error ofψ
with respect toψ
can be denoted and defined by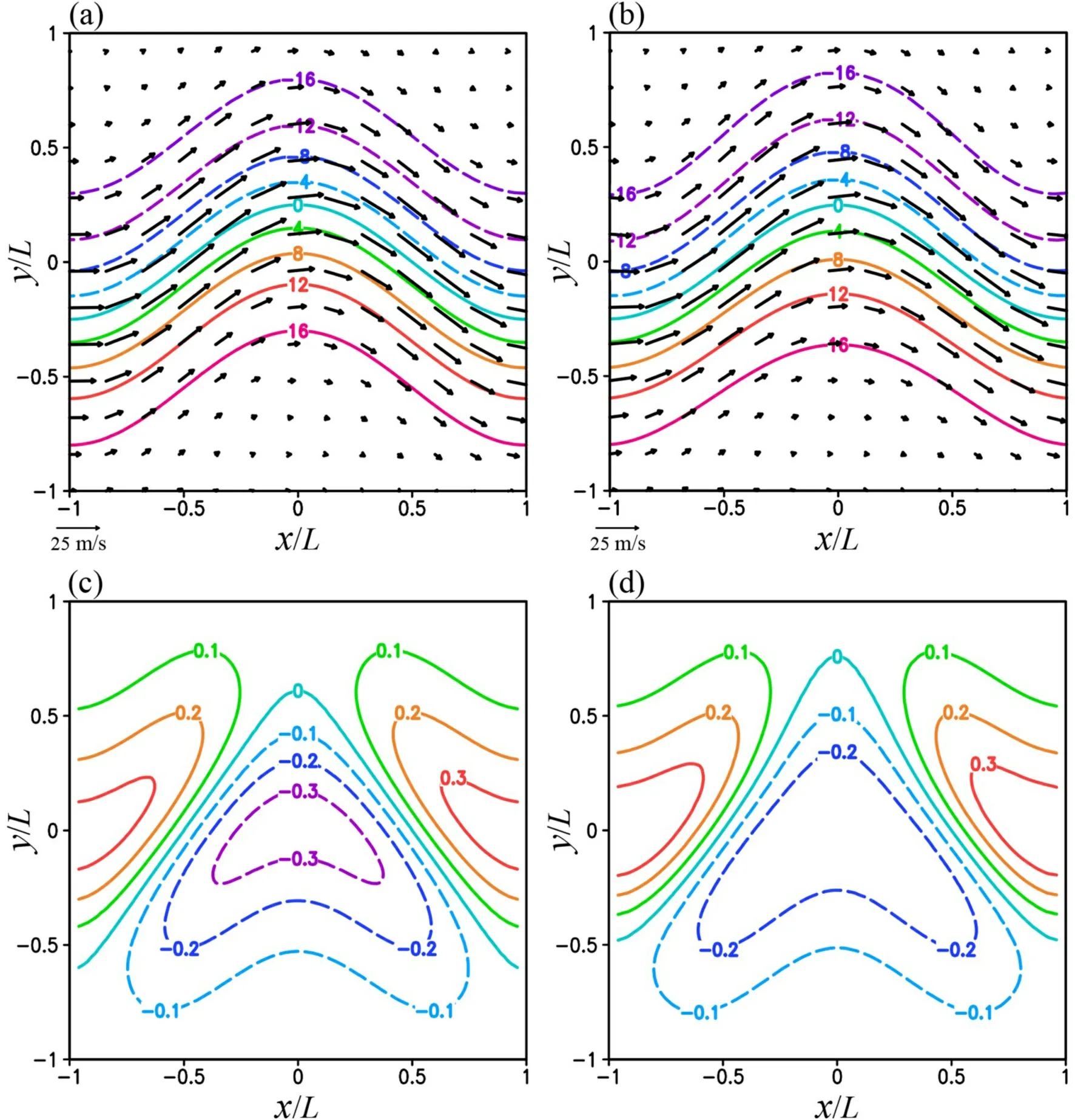
Fig. 1. (a) ψt plotted by color contours every 4.0 in the unit of 106 m2 s−1 and (ut, vt) plotted by black arrows over domain D ≡ [−L ≤ x ≤ L, −L ≤ y ≤ L] with L = 2000 km for the first set of experiments. (b) As in (a) but for ψg and(ug, vg) with ψg ≡ ϕ/f and ϕ computed from ψt by setting f = f0 = 10−4 s−1 as described in section 3.3. (c) Vorticity ζt ≡∇2ψtplotted by color contours every 0.1 in the unit of 10−4 s−1 over domain D. (d) As in (c) but for geostrophic vorticity ζg ≡∇2ψg. The wavering jet axis is along the green contour of ψt = 0 in (a) with its ridge at x = 0 and two troughs at x = ±L on the west and east boundaries of domain D.

ψ
obtained during the iterative process in each experiment can be evaluated by the RMS ofε
(ψ
), denoted and defined by
ψ
can be measured by E[N(ψ
)] defined in Eq. (14).Table 1 lists the values of E(ψ
) and E[N(ψ
)] for the initial guessψ
(=ψ
) in row 1 and the optimally truncated solutionsψ
from the four experiments in rows 2−5. As shown in row 2 versus row 1 of Table 1, M1a reaches the optimal truncation at k = K = 6 where E[N(ψ
)] is reduced (from 0.120 at k = 0) to its minimum [= 2.411×10< E(∇
ϕ
) =3.25×10–the NBE discretization error defined in Eq.(17)] with E(ψ
) reduced (from 2.43×10at k = 0) to 4.87×10. Figure 2a shows that E(ψ
) reaches its minimum(= 4.79×10) at k = 10. This minimum is slightly below E(ψ
) = 4.87×10but undetectable in real-case applications.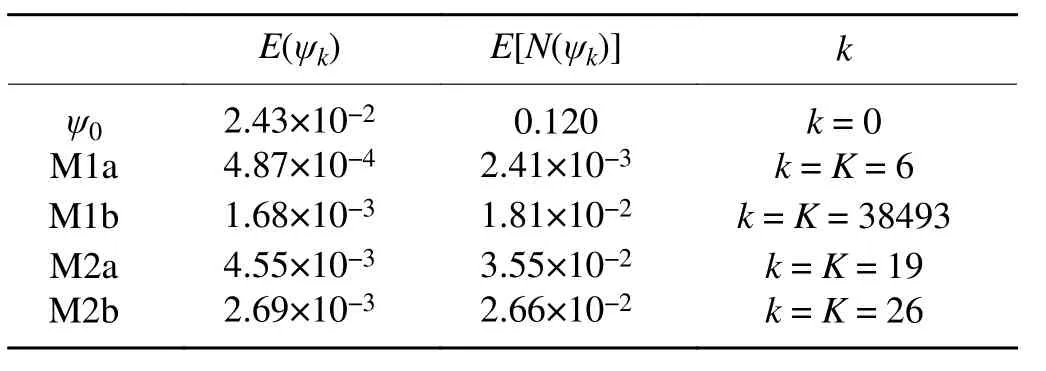
Table 1. Values of E(ψk) and E[N(ψk)] listed in row 1 for the initial guess ψ0 (= ψg) with k = 0 and in rows 2−5 for ψK from the four iterative procedures in the first set of experiments (with Ro =0.1). Here, E(ψk) is defined in Eq. (19), E[N(ψk)] is defined in Eq.(14), k is the iteration number, and ψK is the optimally truncated solution at k = K.
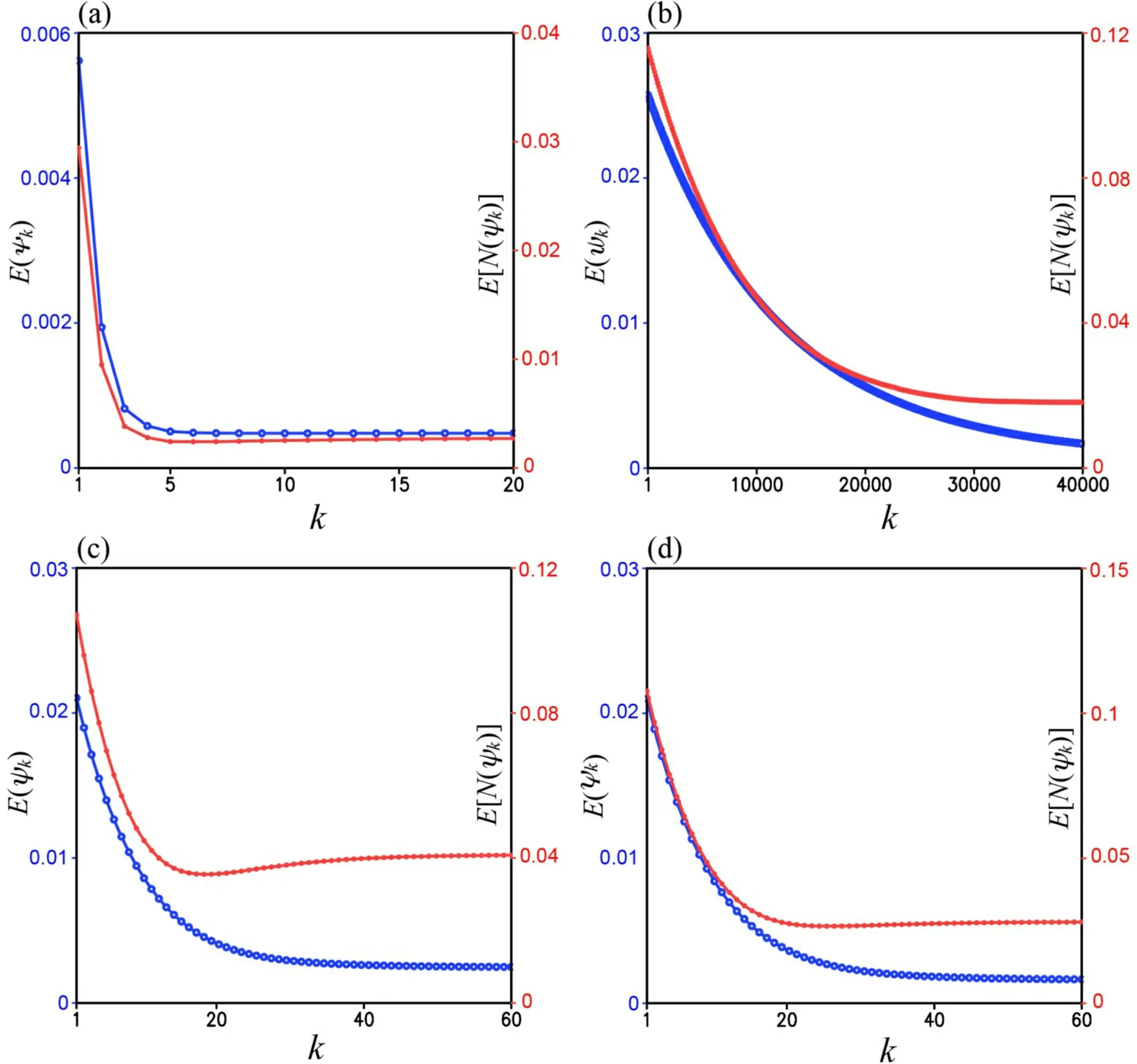
Fig. 2. (a) E[N(ψk)] and E(ψk) from M1a in the first set of experiments plotted by red and blue curves, respectively,as functions of k over the range of 1 ≤ k ≤ 20. (b) As in (a) but from M1b plotted over the range of 1 ≤ k ≤ 4×104.(c) As in (a) but from M2a plotted over the range of 1 ≤ k ≤ 60. (d) As in (c) but from M2b. In each panel, the ordinate of E[N(ψk)] is on the left side labeled in red and the ordinate of E(ψk) is on the right side labeled in blue.
On the contrary, as shown in row 3 of Table 1 and Fig.2b, M1b reaches the optimal truncation very slowly at k =K = 38493 where E[N(ψ
)] is reduced to its global minimum (= 1.81×10) with E(ψ
) reduced to 1.68×10. Here,E[N(ψ
)] has three extremely shallow and small local minima (at k = 32408, 38490 and 38497) not visible in Fig. 2b.These local minima are detected and passed by setting m =3 in Eq. (14) for M1b. Clearly M1b is less accurate and much less efficient than M1a.Figure 2c (or 2d) shows that M2a (or M2b) reaches the optimal truncation at k = K = 19 (or 26) where E[N(ψ
)] is reduced to its global minimum [= 3.55×10(or 2.66×10)]with E(ψ
) reduced to 4.55×10(or 2.69×10), and E(ψ
)decreases continuously toward its minimum [= 2.45×10(or 1.62×10)] as k increases beyond K. Thus, M2a and M2b are less efficient and much less accurate than M1a for Ro = 0.1.4.2. Results from second set of experiments
For this set of experiments,ψ
and (u, v) have the same patterns as those in Fig. 1a, andψ
and (u, v) are similar to those in Fig. 1b, but the contour intervals ofψ
andψ
are reduced by 50% as L is reduced from 2000 to 1000 km with Ro increased to 0.2, so the wavering jet flow is on the subsynoptic scale. In this case, the nonlinearly balanced jet flow is still inertially stable over the entire domain sinceζ
>−f everywhere as shown in Fig. 3a, butζ
< −f/2 in the two small yellow colored areas as shown in Fig. 3b, so the NBE becomes hyperbolic locally in this small area and the boundary value problem in Eq. (1) is not fully well posed.In this case, as shown in row 2 versus row 1 of Table 2,M1a reaches the optimal truncation at k = K = 13 where E[N(ψ
)] is reduced (from 0.243 at k = 0) to its minimum [=5.23×10close to E(∇
ϕ
) = 4.33×10] with E(ψ
) reduced(from 4.86×10at k = 0) to 1.24×10. The rapid descending processes of E(ψ
) and E[N(ψ
)] (not shown) are similar to those in Fig. 2a for M1a in the first set of experiments.As shown in row 3 of Table 2, M1b takes K = 48057 iterations to reach the optimal truncation and the values of E[N(ψ
)] and E(ψ
) at k = K are about four times larger than those from M1a. The extremely slow descending processes of E(ψ
) and E[N(ψ
)] (not shown) are similar to those in Fig. 2b for M1b in the first set of experiments. As shown in row 4 (or 5) of Table 2, M2a (or M2b) reaches the optimal truncation at k = K = 26 (or 35) and the values of E[N(ψ
)]and E(ψ
) are more than (or about) 4 times of those from M1a. Thus, M1a is still more accurate and much more efficient than M1b and is more efficient and much more accurate than M2a and M2b for Ro = 0.2, although the boundary value problem in Eq. (1) in this case is not fully (but nearly)well posed.4.3. Results from third set of experiments
For this set of experiments,ψ
and (u, v) have the same patterns as those in Fig. 1a but the contour interval ofψ
is reduced 4 times as L is reduced from 2000 to 500 km with Ro increased to 0.4, so the wavering jet flow is on the meso-α
scale. Figure 4a shows the fields ofψ
and (u, v)for the nonlinearly balanced jet flow. This nonlinearly balanced jet flow is inertially unstable in the yellow colored area south of the ridge of wavering jet axis in the middle of domain D whereζ
< −f as shown in Fig. 4c. Figure 4d shows thatζ
< −f/2 in the long and broad yellow colored area along and around the wavering jet, so the NBE is hyperbolic in this area and the boundary value problem in Eq. (1)becomes seriously ill-posed.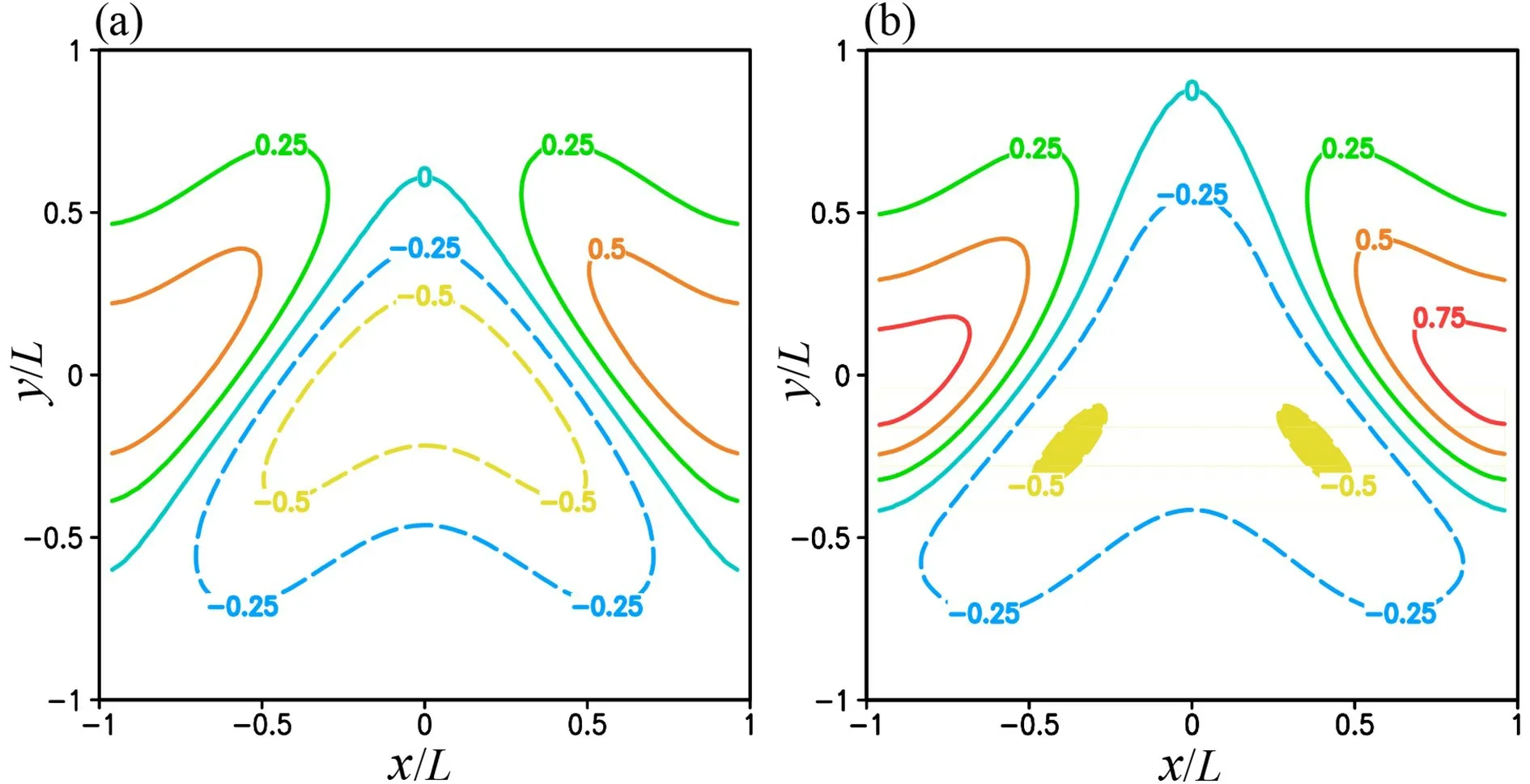
Fig. 3. (a) ζt plotted by color contours every 0.25 in the unit of 10−4 s−1 in domain D with L = 1000 km and Ro = 0.2 for the second set of experiments. (b) As in (a) but for ζg. As shown in (b), ζg < −f/2 (= −f0/2) in the two small yellow colored areas where the NBE becomes locally hyperbolic.
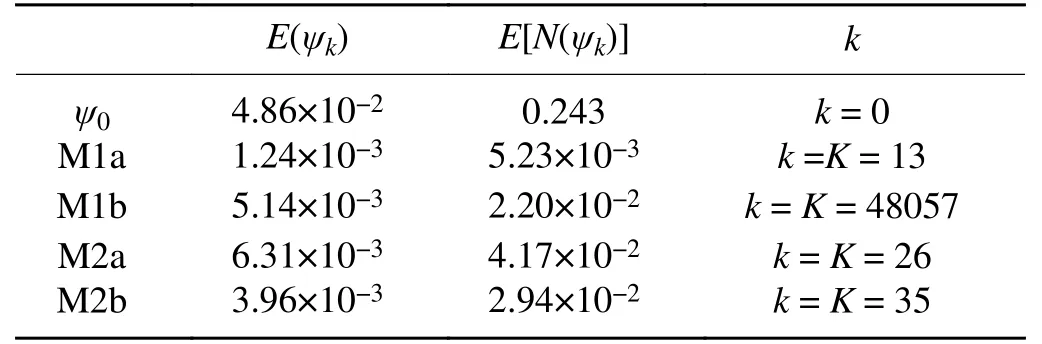
Table 2. As in Table 1 but for the second set of experiments(with Ro = 0.2).
In this case, as shown in row 2 of Table 3 and Fig. 5a,M1a reaches the optimal truncation at k = K = 2 where E[N(ψ
)] is decreased (from 0.57 at k = 0) to its minimum(= 0.13), while E(ψ
) decreases from 9.72×10at k = 0 to 8.20×10at k = K = 2 and then to its minimum (=7.38×10) at k = 6. As k increases beyond 6, M1a diverges.Its optimally truncated solutionψ
is merely slightly more accurate than the initial guessψ
. As shown in row 3 of Table 3 and Fig. 5b, M1b reaches the optimal truncation at k = K = 10325 where E[N(ψ
)] is decreased to its global minimum (= 0.15), while E(ψ
) decreases to 8.31×10at k = K and then to its minimum (= 7.68×10) at k = 23515. Thus,M1b is still less accurate and much efficient than M1a.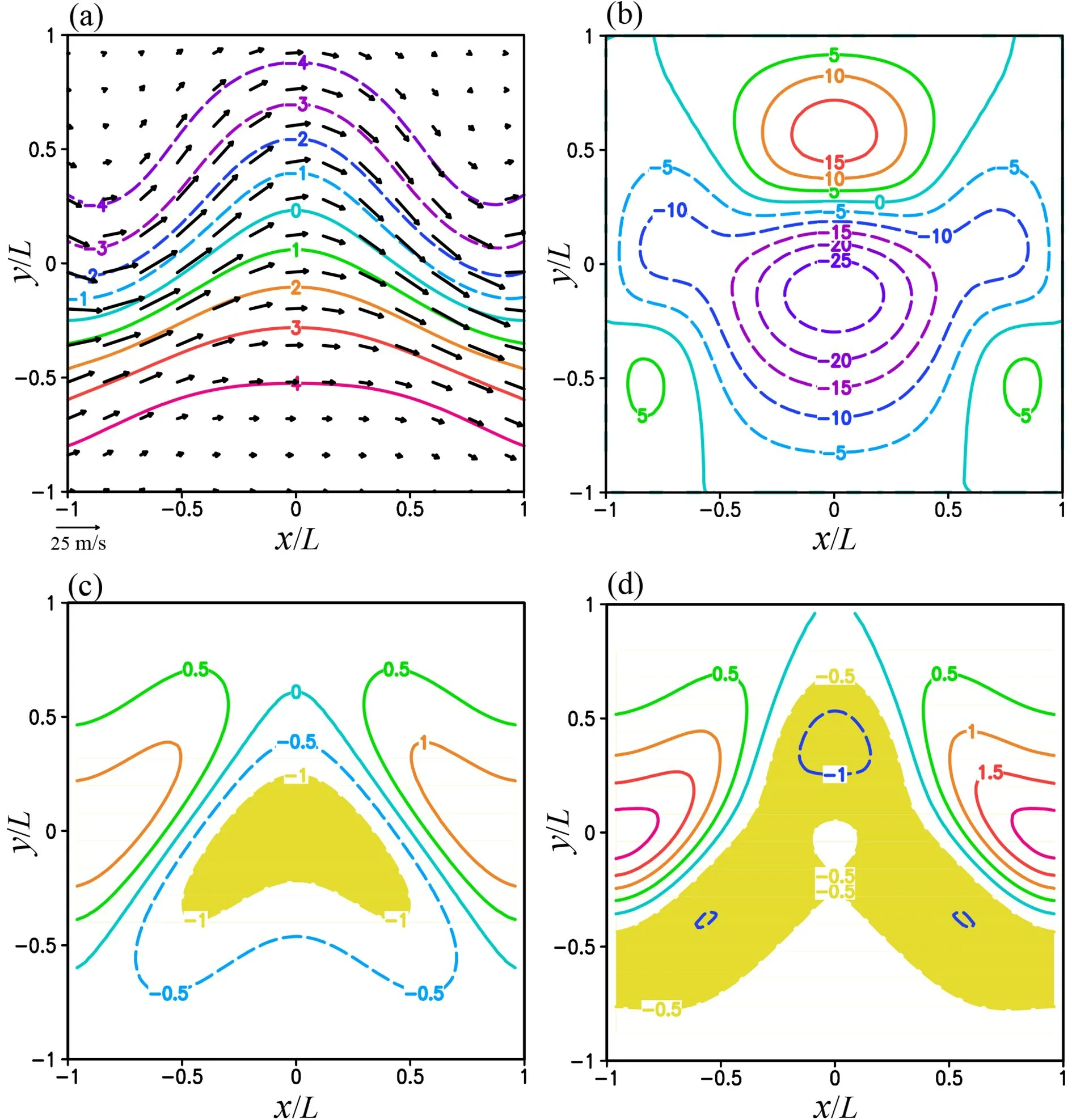
Fig. 4. (a) ψg plotted by color contours every 1.0 in the unit of 106 m2 s−1 and (ug, vg) plotted by black arrows over domain D with L = 500 km and Ro = 0.4 for the third set of experiments. (b) As in (a) but for ε(ψ0) = ε(ψg) plotted by color contours every 5.0 in the unit of 10−2. (c) As in (a) but for ζt plotted by color contours every 0.5 in the unit of 10−4 s−1 in domain D. (d)As in (c) but for ζg. As shown in (c), ζt < −f in the yellow colored area south of the ridge of wavering jet axis where the jet flow becomes inertially unstable. As shown in (c), ζg < −f/2 (= −f0/2) in the long and broad yellow colored area (along and around the wavering jet) where the NBE becomes hyperbolic.
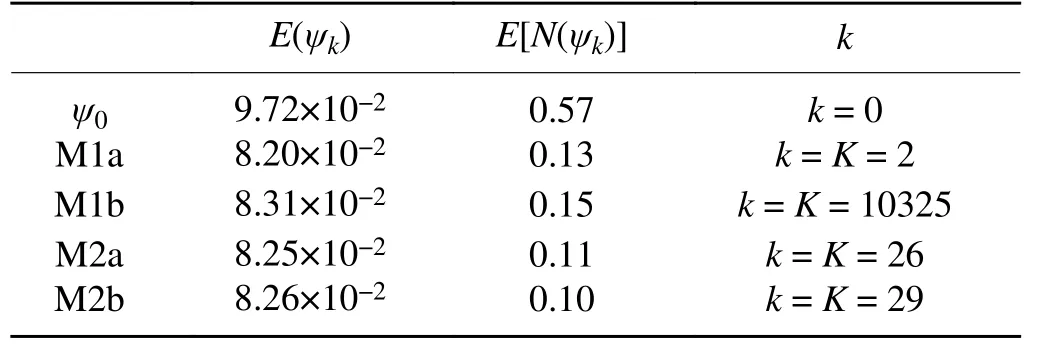
Table 3. As in Table 1 but for the third set of experiments (with Ro = 0.4 and x0 = 0).
Figure 5c (or 5d) shows that M2a (or M2b) reaches the optimal truncation at k = K = 26 (or 29) where E[N(ψ
)] is reduced to its minimum [= 0.11 (or 0.10)], while E(ψ
) is reduced to its minimum [= 8.24×10(or 8.24×10)] at k =25 (or 26) and then increases slightly to 8.25×10(or 8.26×10) at k = K = 26 (or 29). As shown in row 4 (or 5)versus row 2 of Table 3, E(ψ
) from M2a (or M2b) is larger than that from M1a, so M2a (or M2b) is still less accurate than M1a in this case.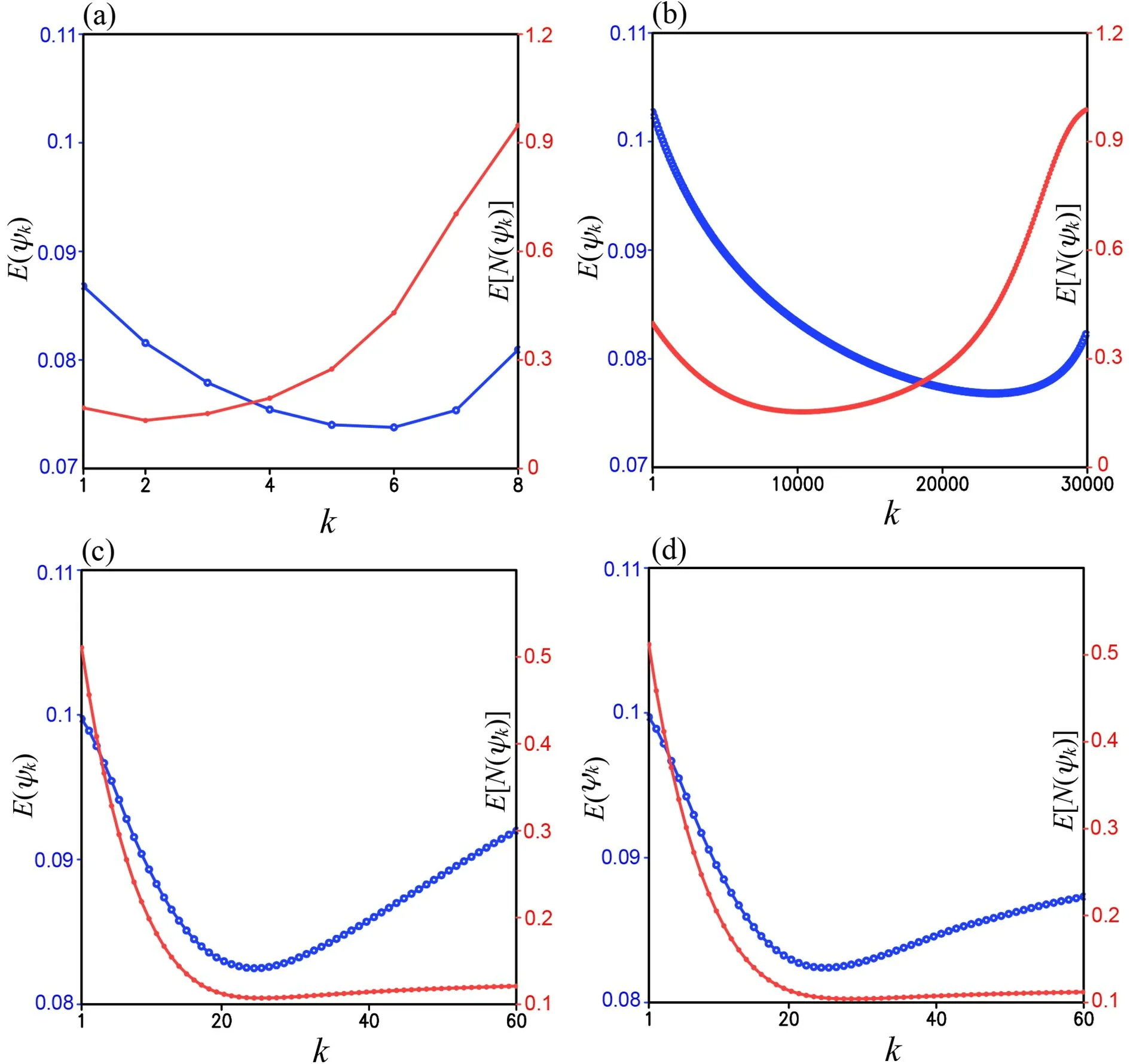
Fig. 5. (a) E[N(ψk)] and E(ψk) from M1a in the third set of experiments plotted by red and blue curves, respectively, as functions of k over the range of 1 ≤ k ≤ 8, (b) As in (a) but from M1b plotted over the range of 1 ≤ k ≤ 3×104. (c) As in (a)but from M2a plotted over the range of 1 ≤ k ≤ 60. (d) As in (c) but from M2b. In each panel, the ordinates of E[N(ψk)] and E(ψk) are placed and labeled as in Fig. 2.

Fig. 6. ε(ψK) plotted by color contours every 0.5 in the unit of 10−2 for ψK from (a) M1a, (b) M1b, (c) M2a and (d) M2b in the third set of experiments.
Figure 6a (or 6b) shows thatε
(ψ
) from M1a (or M1b)peaks positively and negatively in the middle of domain D asε
(ψ
) does in Fig. 4b but with slightly reduced amplitudes. Figure 6c (or 6d) shows thatε
(ψ
) from M2a (or M2b) has a broad negative peak south of the ridge of wavering jet axis similar to that ofε
(ψ
) in Fig. 4b but with a slightly enhanced amplitude. In this case, M1a is still slightly more accurate than the other three iterative procedures, but it cannot effectively reduce the solution error in the central part of the domain where not only is NBE hyperbolic (withζ
< −f/2 as shown in Fig. 4d), but also the jet flow is strongly anti-cyclonically curved and subject to inertial instability (withζ
< −f as shown in Fig. 4c).4.4. Results from fourth set of experiments
For this set of experiments,ψ
and (u, v) are plotted in Fig. 7a. These fields represent the same nonlinearly balanced wavering westerly jet flow as that in the third set of experiments except that the wave fields are shifted by a half-wavelength so the jet flow is curved cyclonically in the middle of domain D. In this case,ψ
and (u, v) are nearly the same as the half-wavelength shifted fields (not shown)from Fig. 4a but with small differences, mainly along and around the trough and ridge lines due to the boundary condition,ϕ
≡ fψ
= fψ
, used here along the two trough lines(instead of the two ridge lines in Fig. 4a) for solvingϕ
from∇ϕ
= N(ψ
). Figure 7c shows that the jet flow becomes inertially unstable in the two yellow colored areas (whereζ
<−f) around the west and east boundaries of domain D. Figure 7d shows that the NBE becomes hyperbolic in the long and broad yellow colored area (whereζ
< −f/2) that is nearly the same as the yellow colored area in Fig. 4d but half-wavelength shifted, so the area ofζ
< −f (that is, the area ofζ
+ f < 0 in which the initial guess field is inertially unstable) in Fig. 4d is moved with the ridge line to the west and east boundaries in Fig. 7d. As the area ofζ
< −f and area ofζ
< −f are moved away from the domain center to the domain boundaries whereψ
is known and given byϕ
/f,the NBE becomes less difficult to solve in this fourth set of experiments than in the third set.
Fig. 7. (a) As in Fig. 4a but for ψt and (ut, vt) in the fourth set of experiments with L = 500 km and x0 = L (instead of x0 = 0).(b) As in (a) but for ε(ψ0) = ε(ψg) plotted by color contours every 6.0 in the unit of 10−2. (c) As in (a) but for ζt plotted by color contours every 0.5 in the unit of 10−4 s−1 in domain D. (d) As in (c) but for ζg.
In this case, as shown in row 2 of Table 4 and Fig. 8a,M1a reaches the optimal truncation at k = K = 7 where E[N(ψ
)] is decreased (from 0.76 at k = 0) to its minimum(= 3.81×10), while E(ψ
) decreases from 9.71×10at k =0 to 2.29×10at k = K = 7 and then to its flat minimum(= 2.25×10) at k = 12, soψ
is significantly more accurate thanψ
and slightly less accurate thanψ
at k = 12(which is undetectable in real-case applications). As shown in row 3 of Table 4 and Fig. 8b, M1b reaches the optimal truncation at k = K = 31830 where E[N(ψ
)] is decreased to its global minimum (= 4.54×10), while E(ψ
) decreases to 2.37×10at k = K and then to its minimum (= 2.21×10)at k = 57 586. Thus, M1b is still much less efficient and less accurate than M1a.
Table 4. As in Table 1 but for the fourth set of experiments (with Ro = 0.4 and x0 = L).
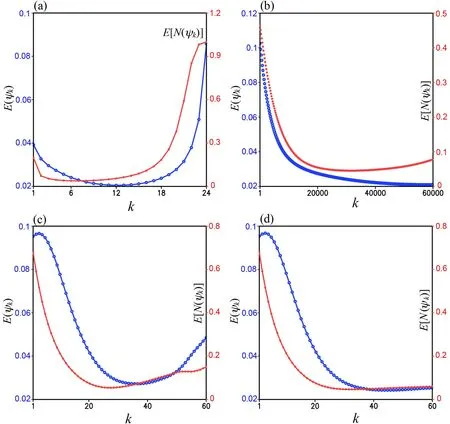
Fig. 8. (a) E[N(ψk)] and E(ψk) from M1a in the fourth set of experiments plotted by red and blue curves, respectively, as functions of k over the range of 1 ≤ k ≤ 24, (b) As in (a) but from M1b plotted over the range of 1 ≤ k ≤ 6×104. (c) As in (a)but from M2a plotted over the range of 0 ≤ k ≤ 60. (d) As in (c) but from M2b. In each panel, the ordinates of E[N(ψk)] and E(ψk) are placed and labeled as in Fig. 2.
Figure 8c (or 8d) shows that M2a (or M2b) reaches the optimal truncation at k = K = 27 (or 32) where E[N(ψ
)] is reduced to its minimum [= 5.42×10(or 4.66×10)], E(ψ
)reduces to 3.03×10(or 2.64×10) at k = K and then to its minimum [= 2.72×10(or 2.43×10)] at k = 36 (or 44), so M2a (or M2b) is still less efficient and less accurate than M1a in this case.Figure 7b shows thatε
(ψ
) has a broad positive (or negative) peak south (or north) of the trough of wavering jet axis in the middle of domain D. These broad peaks are mostly reduced by M1a as shown byε
(ψ
) in Fig. 9a but slightly less reduced by M1b as shown in Fig. 9b and less reduced by M2a (or M2b) as shown in Fig. 9c (or 9d). However, the small secondary negative peak ofε
(ψ
) near the west or east boundary in Fig. 7b is reduced only about 30% by M1a (or M1b) as shown byε
(ψ
) in Fig. 9a (or 9b) and even less reduced by M2a (or M2b) as shown in Fig. 9c (or 9d). Thus,all the four iterative procedures have difficulties in reducing the errors of their optimally truncated solutions near the west and east boundaries where not only is the NBE hyperbolic (withζ
< −f/2 as shown in Fig. 7d), but also the jet flow is subject to inertial instability (withζ
< −f as shown in Fig. 7c). Nevertheless, since the area ofζ
< −f is moved with the ridge of wavering jet axis to the domain boundaries in Fig. 7c, all of the four iterative procedures perform significantly better in this set of experiments than in the previous third set, as shown in Fig. 9 and Table 4 versus Fig. 6 and Table 3. In this case, M1a is still most accurate and M1b is still least efficient among the four iterative procedures.
Fig. 9. ε(ψK) plotted by color contours every 2.0 in the unit of 10−2 for ψK from (a) M1a, (b) M1b, (c) M2a and (d)M2b in the fourth set of experiments.
5. Conclusions
In this paper, two types of existing iterative methods for solving the NBE are reviewed and revisited. The first type was originally proposed by Bolin (1955), in which the NBE is transformed into a linearized equation for a presumably small correction to the initial guess or the subsequently updated solution. The second type was originally proposed by Shuman (1955, 1957) and Miyakoda (1956), in which the NBE is rearranged into a quadratic form of the absolute vorticity and the positive root of this quadratic form is used in the form of a Poisson equation to obtain the solution iteratively. These two types of methods are rederived formally by expanding the solution asymptotically upon a small Rossby number (see section 2), and the rederived methods are called method-1 and method-2, respectively.
Since the rearranged asymptotic expansion is not ensured to converge, especially when the Rossby number is not sufficiently small, a criterion for optimal truncation of asymptotic expansion is proposed [see Eq. (14)] to obtain the super-asymptotic approximation of the solution based on the heuristic theory of asymptotic analysis (Boyd, 1999).In addition, the Poisson solver based on the integral formulas (Cao and Xu, 2011; Xu et al., 2011) is used versus the SOR scheme to solve the boundary value problem in each iterative step.
The four iterative procedures are tested with analytically formulated wavering jet flows on different spatial scales in four sets of experiments. The computational domain covers one full wavelength and is centered at the ridge of the wavering jet in the first three sets of experiments but centered at the trough in the last set. In the first set of experiments, the wavering jet flow is formulated on the synoptic scale [with the half wavelength L = 2000 km and the associated Rossby number Ro = 0.1]. In this case,the NBE is of the elliptic type over the entire domain and therefore its boundary value problem is well posed. In the second set of experiments, the wavering jet flow is formulated on the sub-synoptic scale [with L = 1000 km and Ro =0.2]. In this case, the NBE is of the elliptic type over nearly the entire domain so that its boundary value problem is nearly well posed. In the third (and fourth) sets of experiments, the wavering jet flow is formulated on the meso-α
scale with Ro = 0.4, and the wavering jet flow is curved anti-cyclonically (or cyclonically) in the middle of the domain where the absolute vorticity is locally negative (or strongly positive). In this case, the NBE becomes hyperbolic broadly along and around the wavering jet so that its boundary value problem is seriously ill-posed.The test results can be summarized as follows: For wavering jet flows on the synoptic and sub-synoptic scales, all four iterative procedures can reach their respective optimal truncations and the solution error (originally from the initial guess–the geostrophic streamfunction) can be reduced at the optimal truncation by an order of magnitude or nearly so even when the NBE is not entirely elliptic. Among the four iterative procedures, M1a is most accurate and efficient while M1b is least efficient. The results for wavering jet flows on the synoptic and sub-synoptic scales are insensitive to the location of the wavering jet in the computational domain. In particular, according to our additional experiments (not shown in this paper), when the wavering jet is shifted zonally by a half of wavelength (with the trough moved to the domain center), the solution errors become slightly smaller and the optimal truncation numbers for M1a and M1b (or M2a and M2b) become slightly smaller (or larger)than those listed in Tables 1 and 2. For wavering jet flows on the meso-α
scale in which the NBE’s boundary value problem is seriously ill-posed, the four iterative procedures still can reach their respective optimal truncations with the solution error reduced effectively for cyclonically curved part of the wavering jet flow but not for the anti-cyclonically curved part. In this case, M1a is still most accurate and efficient while M1b is least efficient.In comparison with M1b, the high accuracy and efficiency of M1a can be explained by the fact that the solution obtained by the Poisson solver based on the integral formulas is not only more accurate but also smoother than the solution obtained by the SOR scheme in each step of nonlinear iteration. Consequently, in each next step, the nonlinear differential term on the right-hand side of the incremental-form iteration equation [see Eq. (9a)] is computed more accurately in M1a than in M1b and so is the entire right-hand side. This is especially true and important when the entire right-hand side becomes very small (toward zero) in the late stage of iterations, as it also explains why M1b reaches the optimal truncation much slower than M1a (see Tables 1−4). In comparison with M2a and M2b, the high accuracy and efficiency of M1a can be explained by the fact that the solution in M1a is updated incrementally and the increment is small relative to the entire solution, and so is the error of the increment computed in each step of nonlinear iteration. On the other hand,the solution in M2a or M2b is updated entirely and the entire solution is large relative to the increment and so is the error of the entire solution computed in each step of nonlinear iteration. Moreover, the recursive form of equation [see Eq. (13)] used by M2a and M2b contains a square root term on its right-hand side, so it cannot be converted into an incremental form. Furthermore, this square root term must set to zero when the term inside the square root becomes negative,although the term inside the square root corresponds to the squared absolute vorticity. This problem is caused by the non-negative absolute vorticity assumed in the derivation of the recursive form of equation for M2a and M2b.
Cyclonically curved meso-α
scale jet flows in the middle and upper troposphere are often precursors of severe weather especially when the curved jet flow evolves into a cut-off cyclone atop a meso-α
scale low pressure system in the lower troposphere. In this case, M1a can be potentially and particularly useful for severe weather analyses in the context of semi-balanced dynamics (Xu, 1994; Xu and Cao,2012). In addition, since the mass fields can be estimated from Advanced Microwave Sounding Unit (AMSU) observations, using the NBE to retrieve the horizontal winds in and around tropical cyclones (TC) from the estimated mass fields have potentially important applications for TC warnings and improving TC initial conditions in numerical predictions (Velden and Smith, 1983; Bessho et al, 2006). Applications of M1a in the aforementioned directions deserve continued studies. In particular, the gradient wind can be easily computed for the axisymmetric part of a cutoff cyclone (or TC)and used to improve the initial guess for the iterative procedure. This use of gradient wind can be somewhat similar to the use of gradient wind associated with the axisymmetric part of a hurricane to improve the basic-state potential vorticity (PV) construction for hurricane PV diagnoses (Wang and Zhang, 2003; Kieu and Zhang, 2010). Furthermore,either the gradient wind or the optimal truncated solution from M1a can be used as a new improved initial guess. In this case, the asymptotic expansion can be reformulated upon a new small parameter associated with the reduced error of the new initial guess and this new small parameter can be smaller or much smaller than the Rossby number used for the asymptotic expansion in this paper. The reformulated asymptotic expansion may be truncated to yield a more accurate “hyper-asymptotic” approximation of the solution according to the heuristic theory of asymptotic analysis(see section 5 of Boyd, 1999). This approach deserves further explorations.The authors are thankful to Dr. Ming XUE for reviewing the original manuscript and to the anonymous reviewers for their constructive comments and suggestions. This work was supported by the NSF of China Grants 91937301 and 41675060, the National Key Scientific and Technological Infrastructure Project "EarthLab", and the ONR Grants N000141712375 and N000142012449 to the University of Oklahoma (OU). The numerical experiments were performed at the OU supercomputer Schooner. Funding was also provided to CIMMS by NOAA/Office of Oceanic and Atmospheric Research under NOAA-OU Cooperative Agreement #NA110AR4320072, U.S.Department of Commerce.杂志排行
Advances in Atmospheric Sciences的其它文章
- The Interannual Variation of Transboundary Contributions from Chinese Emissions of PM2.5 to South Korea
- Chen-Chao Koo and the Early Numerical Weather Prediction Experiments in China
- A Case Study of the Initiation of Parallel Convective Lines Back-Building from the South Side of a Mei-yu Front over Complex Terrain
- Parameterized Forward Operators for Simulation and Assimilation of Polarimetric Radar Data with Numerical Weather Predictions
- Impact of the Monsoonal Surge on Extreme Rainfall of Landfalling Tropical Cyclones
- The Asymmetric Atmospheric Response to the Decadal Variability of Kuroshio Extension during Winter
