基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法

王楠 窦智峰 李琰琰 武洁

摘要：针对传统三电平有源中点钳位（ANPC）并网逆变器有限控制集模型预测控制存在的计算流程复杂、中点电压波动较大、输出电流谐波较大的问题，提出了一种基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法.该方法简化了传统模型预测控制方法中建立直流侧中点电压偏移量ΔUdc與三相开关状态Sx中间变量的步骤，在静止αβ坐标系下，利用负载电流i、ΔUdc与Sx之间的关系直接建立数学模型，通过对27种开关状态的实时计算，确定最优输出开关状态.仿真和实验结果表明，该方法有效降低了电流谐波畸变率，达到了抑制中点电压波动的效果.

Abstract：Aiming at the problems of complicated calculation process， large neutral pointe potential fluctuation and large output current harmonic of the traditional three|level ANPC grid|connected inverter limited control set model predictive control， a current control method of three|level ANPC grid|connected inverter based on optimized cost function was proposed. This method simplified the steps of establishing the intermediate variable of the DC side mid|point voltage offset ΔUdc and the three|phase switching state Sx in the traditional model predictive control method.Under the static αβ coordinate system， the relationship between load current i， ΔUdc and Sx was used to directly establish a mathematical model.Through the real|time calculation of 27 switch states， the optimal output switch state was selected.Simulation and experiment result showed that the method effectively reduced the total harmonic distortion rate and achieved the effect of suppressing midpoint voltage fluctuations.

关键词：ANPC并网逆变器;有限控制集模型预测;中点电压波动;三相开关状态

Key words：ANPC grid|connected inverter;finite control set model prediction;mid|point voltage fluctuation;three|phase switching state

中图分类号：TM464

文献标识码：A文章编号：2096-1553（2021）02-0092-10

0 引言

近年来，随着能源需求的不断扩大和环境保护意识的日益增强，电力领域内高转换效率和低谐波含量的分布式可再生能源发电需求不断增加.三电平并网逆变器作为电能转换的主要设备之一，广泛应用于风力发电、储能、微型智能电网、电动汽车等领域.三电平有源中点钳位（ANPC）并网逆变器具有较高的转换效率和灵活的运行方式，在太阳能发电、海上风力发电等新型可再生能源的中高压交流传动、柔性输电、电网无功补偿和吸收等方面都有重要应用[1-3].但中点电压不平衡问题一直是三电平并网逆变器的研究热点，具体表现为中点电压直流偏置和中点电压低频纹波增加，进而对电能转换系统的可靠性造成严重危害[4-6].

在不改变系统结构的前提下，有效的控制策略是解决中点电压不平衡问题的主要方式，其中有限控制集模型预测控制（FCS|MPC）方法已经在两电平逆变器领域得到了广泛应用和深入研究，并取得了较好的经济效益和环境效益.相比传统两电平并网逆变器，三电平并网逆变器具有输出负载电流谐波少、控制效果好等优点，是中压大功率逆变器的主要拓扑结构[7-12]，如何将FCS|MPC方法应用于三电平并网逆变器成为当前的研究热点.FCS|MPC方法基于三电平并网逆变器有限的27种开关组合矢量状态，通过建立三电平ANPC并网逆变器数学预测模型并采用滚动计算代价函数最优解的方法，选择使系统定义的目标函数最小的开关状态作用于逆变器，达到抑制中点电压波动和减少输出电流谐波的目的，具有控制简单、灵活、无需脉宽调制等优点[4-5].针对三电平电压源并网逆变器的中点电压波动问题，在对三电平ANPC并网逆变器建模过程中，传统的模型预测控制方法需要对每相开关状态进行判断，不能直接采用27种开关状态，其控制流程复杂，计算过程时间长，而且控制效率不高，容易导致逆变器开关损耗的增加和中点电压的波动.文献[13]设计了一种在线修正分支定界的方法，其中优化计算部分包含系统跟踪性和开关损耗优化项的指标函数，通过函数来实施滚动优化以达到控制目的.该方法鲁棒性好，在系统多变量受约束的情况下，减少了高次谐波的含量，但计算量较大、控制方法较复杂，对中点电压波动的控制并不理想.文献[14]通过引入基于递推最小二乘法的电感在线辨识算法，提高了三电平并网逆变器系统的参数鲁棒性，但所辨识的电感参数与电感实际值有差异，计算方法稍显复杂.鉴于此，本文拟提出一种基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法，直接以逆变器开关状态对代价函数进行计算和求值，以期减少输出电流的谐波含量，降低中点电压波动，减小总谐波畸变率.

1 三电平ANPC并网逆变器建模

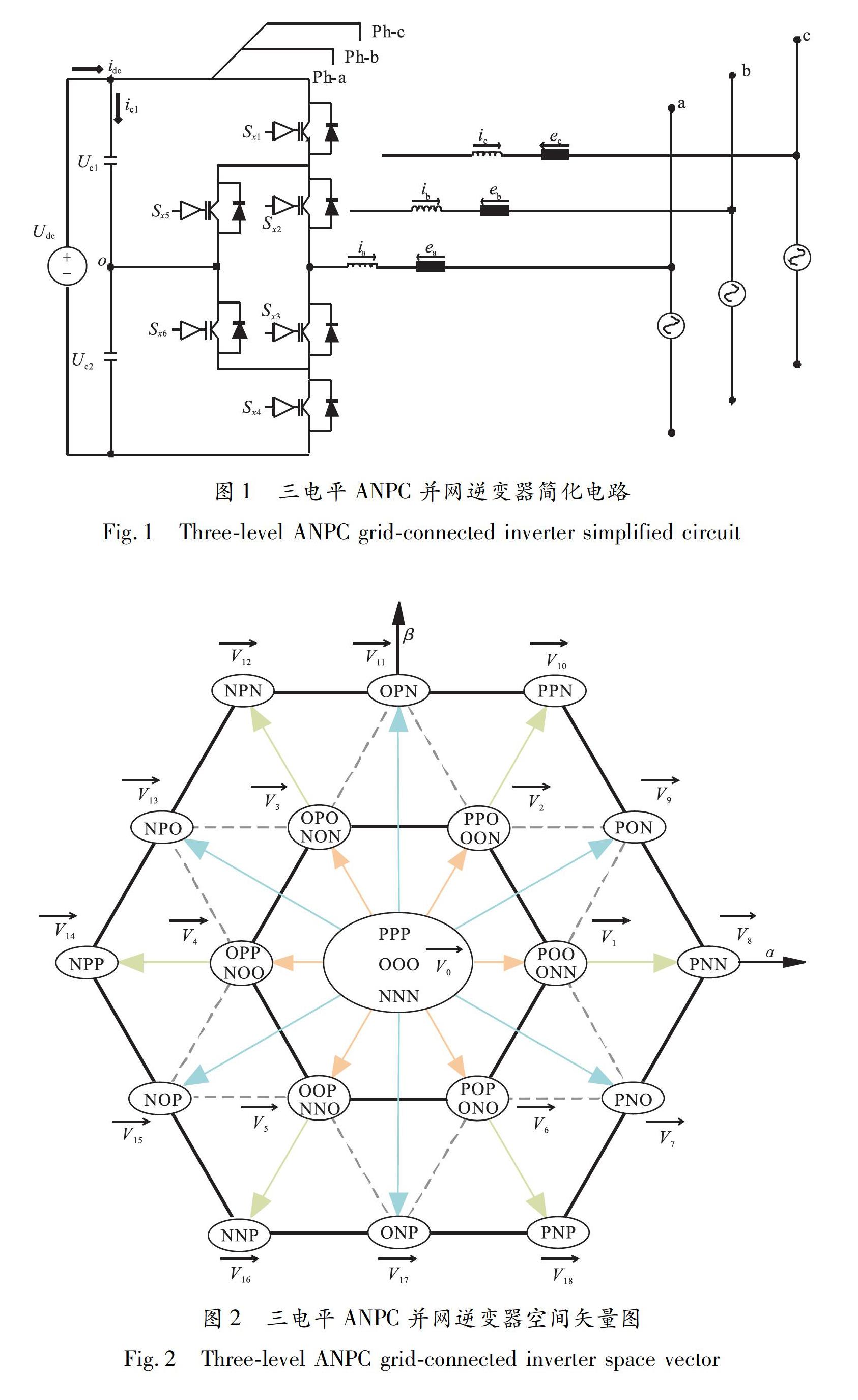
三电平ANPC并网逆变器简化电路如图1所示.由图1可知，三电平ANPC并网逆变器主体结构为三相，每相包括6个开关管，其中2个开关管的中点都连接到直流侧母线电容的中点上.所以，ANPC的每一相相对于直流侧母线电容中性点产生3个相位（Udc/2，0，-Udc/2）.以开关状态变量Sx表示x相的开关状态，这里的x∈{a，b，c}，用符号P、O和N分别表示每相产生的3个相位.三电平ANPC并网逆变器三相产生的空间矢量相位如图2所示.

由图2可知，三电平ANPC并网逆变器三相可产生27种开关状态，其对应电压矢量中有8个冗余矢量（包括2个冗余零矢量），表1为逆变器某一相的开关状态.

3 基于优化代价函数的电流预测控制方法

传统模型预测控制的基本原理是由逆变器输出电流预测值与参考电流值差的绝对值、直流侧两个电容电压的绝对值得到代价函数，求得该代价函数的极小值，即得系统最优解，并输出最佳的开关状态.但是传统方法中增加了电容电压差和开关状态关系的中间变量，使得三电平并网逆变器系统中点电压振荡较高.因此本文直接利用开关状态与电容电压差的关系，建立数学模型，优化传统方法.通过Clark变换，在αβ坐标系下通过系统数学模型充分利用逆变器的离散化特征进行预测算法设计.变换公式可表示为

4 仿真结果与分析

为了验证本文基于优化代价函数的电流预测控制方法的有效性，对传统电流预测控制方法和本文方法进行建模仿真.仿真参数如表2所示，仿真结果如图5—7所示.

由图5可知，在某一段时刻，由于ANPC并网逆变器系统中以某一种开关矢量状态的持续输出作为最优解，造成这段时间内其中点电压波动较大;本文优化方法建立的模型直流侧中点电压波动显著减小，由改进前的60 V降到了改进后的1 V以内，并且波形整体波动更有规律、更加对称，说明其27种开关状态都得到应用.由图6和图7可知，传统方法的输出负载电流波形总体良好，但电流谐波畸变率较高（1.89%）;本文优化方法使得三电平ANPC并网逆变器的输出负载电流谐波畸变率减小至1.14%.

5 实验结果与分析

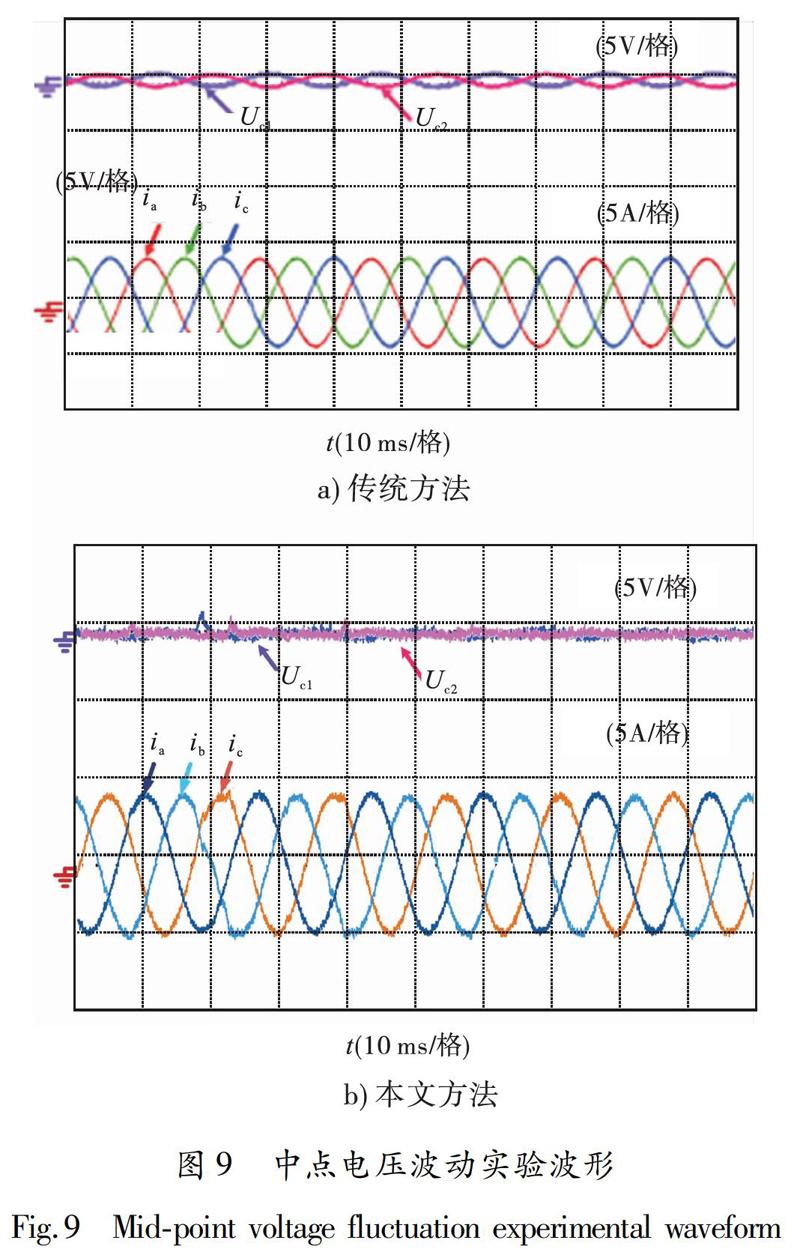
为验证本文方法在实际工程应用中的有效性，设计如下实验平台：直流侧电源采用MywayAPL-II的可编程双向直流电源，交流侧并网部分采用Ametek型号为MX30的可编程交流电源，并采用横河DLM4000系列8通道示波器记录实验结果.实验所用参数与上述仿真参数一致，实验结果如图8—9所示.

由图8可知，优化的模型预测控制方法电流波形效果较好，电流谐波畸变率由3.72%降至3.34%，验证了本文方法的有效性.由图9可知，相比传统有限控制集模型预测电流控制方法，本文方法中点电压波动显著减少，输出电流谐波畸变率得到控制.

6 结论

本文提出了一种基于优化代价函数的三电平ANPC并网逆变器电流预测控制方法，建立了三电平ANPC三相逆变器在静止αβ坐标系下直流侧母线电容中点电压与逆变器输出电流之间的关系，并对传统有限控制集模型预测控制方法和改进的有限控制集模型预测控制方法进行对比.仿真和实验结果表明，本文方法有较好的控制效果，直流侧母线电容电压波动由60 V 降到了1 V以内;改进的有限控制集模型预测控制有良好的稳态性能和优越的动态性能，仿真结果显示电流谐波畸变率由1.89%降至1.14%，实验结果显示电流谐波畸变率由3.72% 降至3.34%.本文只针对单个目标进行预测控制，为了得到更好的控制效果，今后可以进行多个目标同时预测控制研究.

参考文献：

[1] 汪杨俊.模型预测控制在大功率低开关频率并网逆变器中的应用[D].合肥：合肥工业大学，2015.

[2] ZHANG Y C，BAI Y N.Model predictive flux control of three|level inverter|fed induction motor drives based on space vector modulation[C]∥2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia （IFEEC 2017|ECCE Asia）.Piscataway：IEEE，2017：986.

[3] BEKHOUCHA N，MESBAHI N，OUCHEN S.Predictive current control of three level neutral point clamped grid connected inverter in photovoltaic generation systems[C]∥2018 International Conference on Electrical Sciences and Technologies in Maghreb （CISTEM）.Piscataway：IEEE，2018：1.

[4] 许杭蓬，陈权，李国丽，等.基于改進SVPWM的三电平NPC逆变器中点电压平衡的研究[J].现代电子技术，2019，42（4）：129.

[5] 黄竞智，吴雷，沈佳烨.NPC型三电平逆变器的中点电位控制方法研究[J].电子测量技术，2019，42（3）：40.

[6] 潘镜元，赵香花，朱大为，等.基于三电平NPC逆变器的并网控制策略[J].电气自动化，2018，40（4）：9.

[7] 沈坤，章兢，王玲，等.三相电压型逆变器模型预测控制[J].电工技术学报，2013，28（12）：283.

[8] 邓知先，宋文胜，曹梦华.单相PWM整流器模型预测电流控制算法[J].中国电机工程学报，2016，36（11）：2996.

[9] 张永昌，蔡倩，彭玉宾，等.带参数辨识功能的三电平变换器高效模型预测控制方法[J].电气工程学报，2018，13（4）：1.

[10]PERANTZAKIS G，XEPAPAS F，PAPATHANASSIOU S，et al.A predictive current control technique for three|level NPC voltage source inverters[C]∥2005 IEEE 36th Power Electronics Specialists Conference.Piscataway：IEEE，2005：1241.

[11]YARAMASU V，WU B.Predictive control of a three|level boost converter and an NPC inverter for high|power PMSG|based medium voltage wind energy conversion systems[J].IEEE Transactions on Power Electronics，2014，29（10）：5308.

[12]CHEN X T，GAO N，WU W M，et al.Finite Control set model predictive control for LCL|filter|based grid|tied npc inverter[C]∥2018 IEEE International Power Electronics and Application Conference and Exposition （PEAC）.Piscataway：IEEE，2018：1.

[13]劉斌，夏龙清，李俊，等.并网逆变多目标约束预测控制器设计及在线算法[J].中国电机工程学报，2014，34（30）：5277.

[14]DADU A M，SOON T K，MEKHILEF S，et al.Lyapunov law based model predictive control scheme for grid connected three phase three level neutral point clamped inverter[C]∥2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia （IFEEC 2017|ECCE Asia）.Piscataway：IEEE，2017：512.