基于核相关滤波器的高置信度自适应融合目标跟踪算法研究

夏 婷 谢维信 陈富健 黄梓桐

(深圳大学ATR国防科技重点实验室, 广东深圳 518060)

1 引言

视频目标跟踪的方法有很多,一般总结为生成式方法和鉴别式方法[1]。生成式模型利用的是稀疏编码,即线性系数向量的分量稀疏表示成多个0,相当于求解问题的近似过程。这类方法中比较经典的代表有基于概率密度分布的Meanshift算法、基于粒子分布的Particle Filter算法、基于特征点的光流算法等。此类算法不足是未全面利用视频序列的信息,导致跟踪不够稳定。鉴别式模型是目前常用的目标跟踪算法,它改进了生成式模型算法的不足,充分利用图像的整个信息,将整张图像中的前景与背景的信息相比较,然后将需要的信息提取出来获得目标的准确位置。目前此类算法中得到广泛应用的是基于核相关滤波器的目标跟踪算法[2]。

核相关滤波最早期比较注重速度,Bolme的MOSSE算法和Martins的CSK算法最具有代表性[3]。Martins在算法CSK基础上改进的算法KCF中又引进快速傅里叶变换(FFT)[4],进一步降低计算量。但是仅注重速度的目标跟踪在实际的应用中是存在问题的,因为目标跟踪是一个十分复杂的过程,可以概括成11种挑战[5- 6]:亮度变化(Illumination Variation,IV)、背景杂波(Background Clutter,BC)、形状变化(Deformation,DEF)、目标尺度变化(Scale Variation,SV)、快速运动(Fast Motion,FM)、受到遮挡(Occlusion,OCC)、运动模糊(Motion Blur,MB)、分辨率较低(Low Resolution,LR),超出视野(Out-of-View,OV),平面内外旋转(out-of-plane Rotation&in-plane Rotation)等。同时解决这11种甚至更多的目标跟踪场景中的复杂问题并不容易,研究者往往针对不同的情况进行专门完善或者对几种情况进行综合完善与改进。例如KCF算法中引进循环采样来增加样本数量以此解决稀疏采样问题以及利用FFT快速傅里叶变换降低计算量;DSST算法利用两个独立的滤波器(位置滤波器和尺度滤波器)专门解决目标尺度变化问题[7];SAMF[8]算法利用颜色和梯度的互补特性简单引入尺度池方法以及双线性插值方法,其目的也是专门针对目标尺度变化问题进行改进。但是在实际的应用中目标的位置变化是比尺度变化要更加明显,因此在位置变化方面的跟踪效果不是很稳定。DAT算法是利用贝叶斯方法计算出前景和背景的颜色概率图,单纯利用统计颜色特征方法进行目标跟踪。Staple[9]算法打破单一模板特性,利用两种独立模板单独训练和测试,在响应阶段进行线性融合,相当于DSST算法和DAT算法的优势联合,达到高跟踪速度同时有效改善了跟踪的性能。

由于目标跟踪中目标形态以及所处的环境很复杂,研究者仍然对基于核相关滤波的目标跟踪领域不断完善和突破,大致方向一般趋向于提出一种新的针对性算法,或者几个算法的融合,或者将算法自适应等。例如,杨晓辉等人提出的《A Joint Multi-Feature and Scale-Adaptive Correlation Filter Tracker》[10],利用位置相关滤波器和比例相关滤波器的相结合,通过梯度直方图特征(HOG)和颜色特征来计算目标的位置,利用比例滤波器识别响应的大小判断,两者的结合提高了跟踪的性能;Kenan Dai, Dong Wang等人提出《Visual Tracking via Adaptive Spatially-Regularized Correlation Filters》[11],利用自适应空间正则化相关滤波器模型优化滤波器系数和空间正则化权重,在多个算法支持下取得效果;李大雷、陆瑞涛、杨小刚等人提出的《Object Tracking Based on Kernel Correlation Filter and Multi-feature Fusion》[12],首先将图像的灰度特征、梯度直方图特征和LAB特征相结合提高跟踪器的鲁棒性,其次利用当前帧模型与初始帧模型的相似度值来解决目标被遮挡问题,最后引入多尺度滤波器改善尺度变化以此缓解跟踪漂移的问题。总之,核相关滤波跟踪在向自适应和融合方向发展。

以上算法同时使用的方法均是针对每一帧目标实时更新滤波器模板,这种方法的优点在于,随着目标外观的不断变化,滤波器不可能仅仅只学习前几帧的外观统计特性,因为目标跟踪过程中的非平稳信号的噪声会随着目标统计特性的变化而变化,滤波器模板不更新,跟踪的效果就会越来越差。而每一帧实时性的模板更新也会带来更大的问题,通过目标的位置获得新一帧的特征图,再用新特征图更新滤波器模板,并没有完全考虑新特征图的可靠性,当目标受到遮挡、强烈光照或者运动模糊等情况时,当前帧获得的特征图实际上是不准确的,用不准确的特征图获得不准确的滤波器模板,随着跟踪帧数的叠加就会导致跟踪的漂移甚至失败。针对此种情况Wang M, Liu Y等提出了LMCF算法[13],通过检测图像响应值的最大峰值以及多峰响应值的平均能量来约束滤波器模板的更新,从而降低因更新不准确的滤波器模板造成目标丢失的情况。但是LMCF算法仍然是建立在单一模板基础上进行改进的,对于算法的融合以及自适应等跟踪问题并不能够解决。

针对上面的问题,本文提出将LMCF算法和双模板特征的Staple算法相融合的LMCF-Staple算法。文章思路为首先利用贝叶斯公式分别计算出当前帧的前景和背景的概率图[14-15],对前景直方图和背景直方图进行均衡化,以去除一部分噪声;其次,利用直方图匹配方法消减目标和背景过于相似的问题,通过巴氏系数计算出当前帧的背景和前景的直方图的相似度值;再次,利用数据分析设定阈值,根据阈值将直方图的bin值进行自适应,以此提高跟踪的分辨率;然后利用LMCF算法求出当前帧图像与当前帧的前五帧图像的平均相关峰值能量(APCE)以及求取出目标响应值的最大值,根据数据分析设定阈值,阈值范围内的继续更新滤波器模板,阈值范围外的停止更新模板;最后,将阈值范围内的最大值和APCE值与融合系数相结合,使算法同时又达到了自适应的最优融合。

2 核相关滤波目标跟踪算法

2.1 Staple目标跟踪算法

Staple算法融合了KCF算法中的核相关滤波器模板以及颜色直方图特征的模板。算法在训练和测试阶段均单独运行。相关滤波器模型中利用HOG特征进行训练和测试目标模板,并将当前帧图像和之前帧的图像通过给定的学习率进行结合来更新滤波器模板;颜色直方图特征分类器利用贝叶斯公式计算出目标的概率直方图,来提取目标特征,以此匹配更好的响应目标,然后训练与更新直方图分类器;最后将核相关滤波器和直方图分类器的响应按照固定的比例进行线性融合,得到最终的响应。

融合响应公式如下:

f(x)=γtmplftmpl(x)+γhistfhist(x)

(1)

ftmpl(x)表示滤波器模板响应,γtmpl表示滤波器模板的权重系数,fhist(x)表示直方图特征的响应,γhist表示直方图特征的权重系数。

训练滤波器的公式为:

(2)

训练直方图分类器的公式为:

(3)

滤波器模板更新的函数为:

(4)

(5)

直方图分类器更新的函数为:

(6)

(7)

其中使用的损失函数为:

L(θ;χt)=(1-η)L(θ;χt-1)+ηl(xt,pt,θ)

(8)

令α=γhist,称作算法的融合系数,则最终融合公式为:

f(x)=ftmpl(x)(1-α)+fhist(x)α

(9)

公式中各个符号含义见文献[9]。

Staple算法将两个特征按照一定权重进行融合,最终的跟踪效果不仅增强了跟踪的稳定性、准确性以及重合率,同时提高了跟踪的速度,其跟踪速度高达80 fps,由此引起研究者们的强烈关注,对后续的跟踪算法领域产生很大的影响。

2.2 LMCF目标跟踪算法

LMCF算法结合了Struck算法的结构化支持向量机(SVM)和KCF算法中的循环矩阵以及FFT的优点,既保留跟踪的高速度又提高跟踪的性能。LMCF算法主要提出了两个创新点,第一个创新点是利用多峰检测来解决目标被相似物体或者背景干扰的问题,作者设定目标函数的响应为:

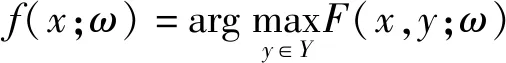
(10)

当下一帧到来,通过KCF中的循环采样获得图像的响应值:

(11)

算法计算出响应值的峰值,当无任何干扰时,响应值为单一的峰值,即目标所在的中心位置;当有相似物体干扰或者遮挡时出现多个峰值,此时的干扰物的峰值很有可能高于目标的峰值,容易引起误判。因此,此算法设定了阈值θ,当多个峰值和最高峰之间的比率大于预定义的阈值θ时,通过等式进行重新检测以这些峰值为中心的响应图的区域,最终确定这些响应图中的最大峰值作为目标的响应值。

第二个创新点是将响应的最大峰值和平均峰值相关能量结合,判断滤波器模型是否需要更新。平均峰值相关能量(average peak-to correlation energy, APCE)表示为:

(12)

仅利用最大峰值判据目标的位置和滤波器的更新容易引起目标的漂移甚至丢失。当目标受到干扰时,响应图会产生剧烈波动,使得模型和真正的响应存在极大偏差,如果继续使用不确定的响应来更新滤波器模型将会使跟踪的性能越来越差。因此,算法中规定当响应的最大值和APCE值均以一定比率大于前面所有帧的平均值时,目标的模型才更新。最终LMCF算法在数据集上进行测试的实验结果显示,其运行速度高于Staples算法的80 fps,跟踪的精度和稳定性也有一定提高。

3 LMCF-Staple目标跟踪算法

为了解决目标跟踪过程中的目标漂移甚至丢失的情况,我们提出LMCF-Staple算法。和LMCF算法的不同之处在于,首先,我们增加了直方图匹配方法,并对直方图进行均衡化,以去除一部分噪声;其次,利用贝叶斯公式计算出当前帧的前景和背景的概率直方图,通过巴氏系数求解出当前帧的前景和背景的相似度值;再通过数据分析设定阈值,按照所设定的阈值与前面求得的直方图的相似度值结合,将直方图bin值自适应化,来提高跟踪的分辨率;然后,为了降低计算量,这里仅计算了前五帧视频序列的响应最大值和APCE值,并根据数据分析设定阈值,当响应最大值和APCE值均大于前五帧的平均值时,滤波器模板才进行更新,此种方法被称作高置信度计算;最后,将最大峰值和APCE值根据一定的线性比例和Staple算法中的融合系数α相结合,使跟踪达到自适应融合。

3.1 直方图匹配

在直方图计算中,Staple算法将直方图bin值固定为32,利用贝叶斯公式计算出目标似然图:

PO=Pfg./(Pfg+Pbg)

(13)

“./”表示矩阵之间相除;PO表示目标似然图,Pfg表示前景似然图;Pbg表示背景似然图。然后利用目标似然图计算出前景和背景的概率函数:

POfg=PO.*fgmask

(14)

PObg=PO.*bgmask

(15)

POfg表示前景占比目标的概率;PObg表示背景占比目标的概率,fgmask、bgmask表示前景和背景的面积中每一点所构成的矩阵,这点在文献[3]中有详细说明。

然后为了降低噪声,这里增加了直方图均衡化,伪代码如下:

fghist=histeq(fghist)

(16)

bghist=histeq(bghist)

(17)

巴氏系数在文献[3]中讲到,可迭代或者积分出两个函数之间的重叠部分的面积,一般用来测量样本间的距离,很适合应用于图像相似度的测量计算。在本文中,将一张图片的前景和背景的直方图分别求解出来,然后利用巴氏系数分别计算每张视频序列内容中前景和背景的值,当值比较大时,说明颜色十分相似,当值比较小时,说明颜色区分明显。以下给出巴氏系数的主要公式:

(18)

本文“⊙”表示相乘,设定阈值为β1,当H在阈值范围内时,说明颜色相似度可以区分,跟踪不易出错,bin值保持不变,当H超过阈值,说明颜色相似度值比较高,跟踪容易产生错误,bin值变化。利用此种方法提高了跟踪的分辨率。

3.2 高置信度计算

通过观察目标的响应峰值,发现当目标受到干扰时,峰值从单一峰变为多峰,响应图如下:

第一帧没有扰动,峰值和APCE值为:

Mcf1=0.70,APCEcf1=64.05

(19)

后面开始有干扰,第13帧可以看到穿白色球衣的球员遮挡了目标的一部分,加上目标本身的形态在不断变化,导致出现多个峰值,此时的峰值和APCE值为:

Mcf13=0.15,APCEcf13=4.25

(20)

很明显,当目标受到各种干扰时,APCE值急剧下降。因此,通过APCE值来评判目标的位置是很好的一种方法[16-18]。

为了降低计算量,LMCF-Staple算法并没有将当前帧之前的所有帧数的响应峰值和APCE值求取平均值,通过实验验证,仅提取当前帧的前五帧的平均值误差就极其微小。响应峰值表示为:M_cf、M_pwp、M,APCE值表示为:APCE_cf、APCE_pwp、APCE,其中cf、pwp分别表示HOG特征和颜色直方图特征。当当前帧的峰值和APCE值同时大于当前帧的前五帧的平均值时,更新直方图滤波器和尺度滤波器,否则停止更新所有滤波器,进一步降低了因之前模板不准确而继续使用其模板的累积误差[19]。

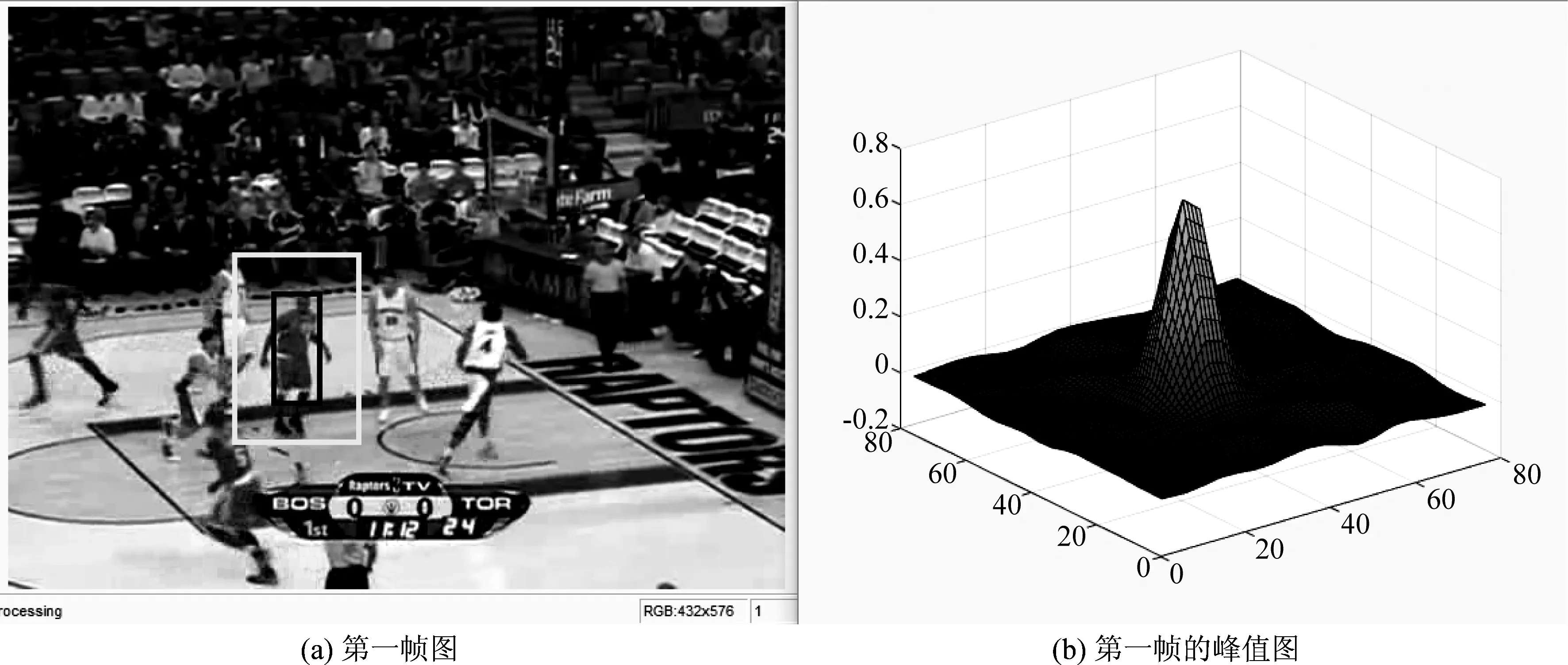
图1 第一帧图和对应的峰值图Fig.1 The first frame image and the corresponding peak image

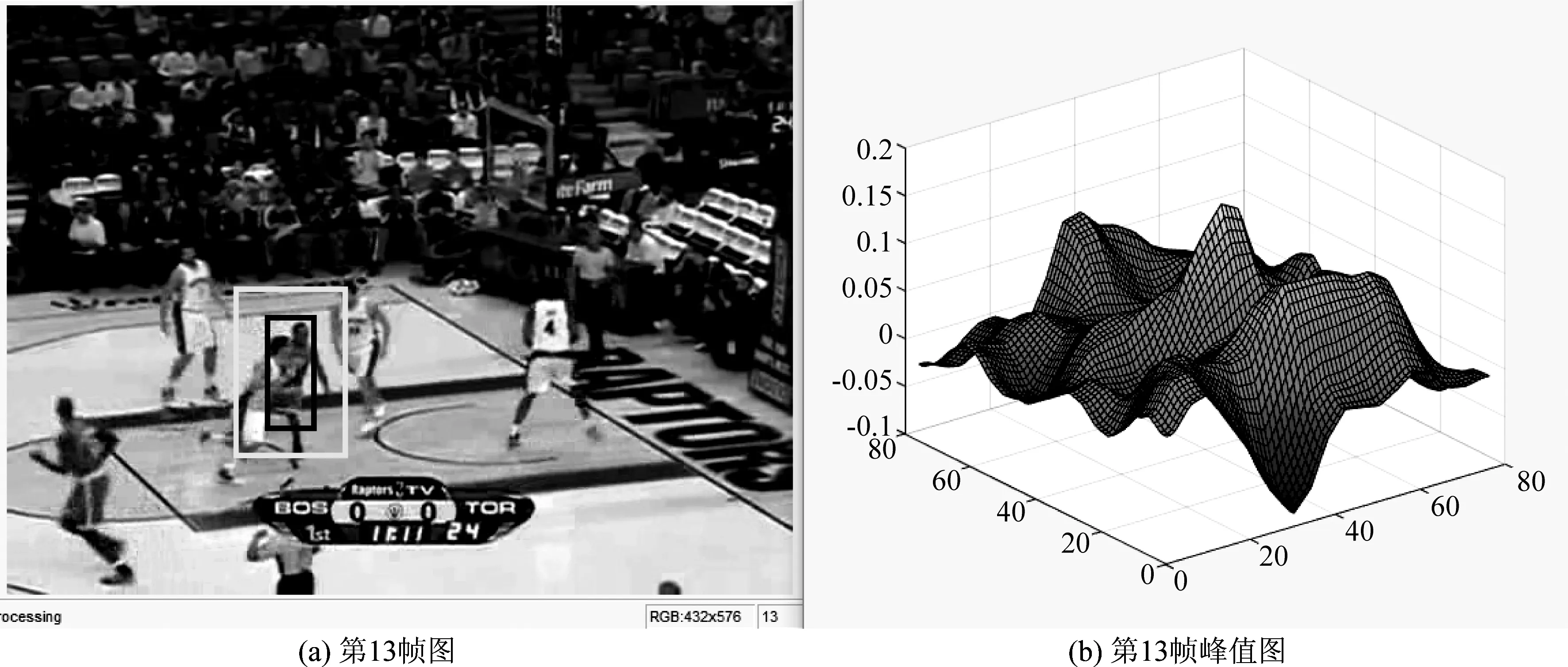
图2 第13帧图和对应的峰值图Fig.2 The 13th frame image and the corresponding peak image

3.3 自适应融合

Staple算法将融合系数α固定,而HOG特征适合于颜色变化的跟踪,但对于形变和模糊就不那么理想;直方图特征适合于形变和运动模糊的跟踪,对于颜色变化就十分敏感。因此,固定的权重并不能很好的利用HOG特征和颜色直方图特征。在LMCF-Staple算法中,融合系数是动态调整的,算法将当前帧的两个特征的APCE值与已经融合后的APCE值进行线性结合,然后通过数据分析设定阈值β2,β3,以及给融合系数适合的比率γ1,γ2。公式如下:

(21)

(22)

(23)

当M小于β2且M大于β3时,

α=γ1⊙r

(24)

当M小于β3时,

α=γ2⊙r

(25)

其他情况α值不变化,最后将α应用于Staple算法的融合公式中为:

(26)

LMCF-Staple算法通过直方图匹配、高置信度以及自适应的融合大大降低了算法的漂移特性,不仅提高了算法的稳定性,同时算法的精确度、成功率以及跟踪的速度都有一定的提高。算法的大致流程如图3所示。

图3 算法流程图Fig.3 Algorithm flow chart

4 实验结果和分析

LMCF-Staple算法的实验平台为:处理器是Inter(R) Core(TM) i5-3470 CPU @3.20 GHz,内存是8.00 GB,64位操作系统,2018a版MATLAB。实验中固定的参数有,HOG特征的cell为4*4,模板学习率ηtmpl=0.01,直方图学习率ηhist=0.04,γ1=0.12,γ2=0.15。跟踪针对的情况为前文提到的11种挑战。实验对比的算法有,Staple、DSST、SAMF、KCF、CSK,测试的数据集为OTB50、OTB100、VOT2016,实验在OTB上的评估指标为成功率和精确度,成功率公式为:

(27)

rt指候选框,ro指人工标注的跟踪框。

精度公式为:

(28)

Nt、Ns分别指第t帧帧数和总帧数。

实验在VOT2016数据集上的评估指标为精度和鲁棒性[20-22],精度的衡量方式是平均重叠率,利用了前一帧和下一预测帧图像的ground truth面积的交并比,其公式为:

(29)

鲁棒性指跟踪器的稳定性,一般指跟踪器在数据集测试中跟丢的目标次数,数值越大,稳定性越差。而一般在绘制鲁棒性图时取递减的自然对数来描述,所以A-R图中的鲁棒性值越大表示越稳定。公式如下:

RS=e-SF

(30)

F指跟丢的次数,S是人为标定的数值,只是影响A-R图归一化时数值所处的范围。

4.1 OTB数据集实验测试的综合性能分析

LMCF-Staple算法通过在大型数据集OTB50和OTB100上与当前主流的五个算法Staple、DSST、SAMF、KCF、CSK进行对比测试;两个数据集一共有100个具有跟踪挑战性的视频序列,情况包含背景杂波、尺度变化、移除视野、形变、遮挡等11种挑战。测试的最终精确度图和成功率图为:

图4是LMCF-Staple算法在OTB50数据集上的测试结果,由图可知LMCF-Staple算法的精度和成功率分别为:0.702、0.634,而排在第二位的Staple算法的精度和成功率为:0.674、0.606,LMCF-Staple算法的精度比排在第二的Staple算法高出2.8%,准确率高出2.8%。图5是LMCF-Staple算法在OTB100数据集上的测试结果,其精度和成功率分别为:0.781、0.705,排在第二位的Staple算法分别为:0.767,0.703,因此精度和成功率分别提高了1.4%、0.2%。由此可以看出LMCF-Staple算法得到了优化,尤其是在精确度方面提升比较高,这主要得益于利用最大峰值和高置信度估计与Staple算法的结合,去掉了不确定的更新模板,使算法更加稳定可靠。

另外,实验中针对11种挑战情况下的数据进行了大量的分析,然后设定了合适的阈值和比率,这里列出具有代表性的OTB100的数据表格如下所示:

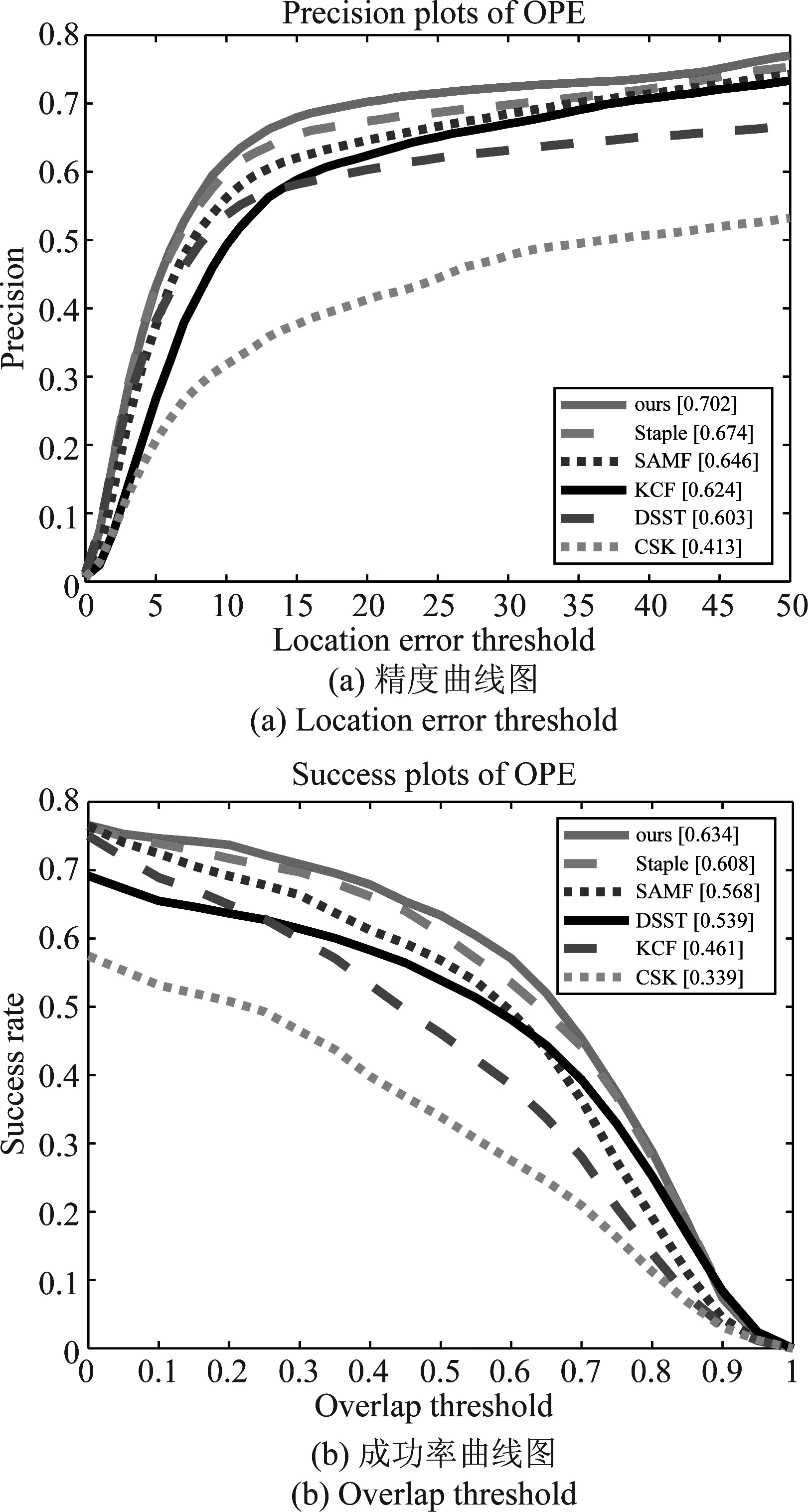
图4 OTB50数据集的综合评价曲线图Fig.4 Comprehensive evaluation curve of OTB50 data set

图5 OTB100数据集的综合评价曲线图Fig.5 Comprehensive evaluation curve of OTB100 data set

表格中的黑色代表最大的数值,斜体代表排在第二位的数值。从表格中可以看出在精确度方面LMCF-Staple算法的OPR/SV/OCC/DEF/OV/BC均排在第一位,其他几种情况分别排在第二或者第三位,在成功率方面OPR/SV/OCC/OV/BC/LR排在第一位,其他几种分别排在第二和第三位。综合情况是6个算法中最优的。在出现背景杂波、尺度变化、移除视野和平面外旋转的四种情况下,均表现出最优的跟踪性能,在遮挡、形变情况下的精确度也是最高,同时分辨率也得到很大的提高,但是也可以看到在快速运动下的模糊目标跟踪仍然不是过于理想,这是因为HOG特征和直方图特征本身的缺陷性,当快速运动出现模糊时,HOG特征就会超出它本身的极限性,同时直方图特征对于颜色的分辨能力也不足,就会造成目标的稍微漂移,后续对于这种情况需要进一步研究。

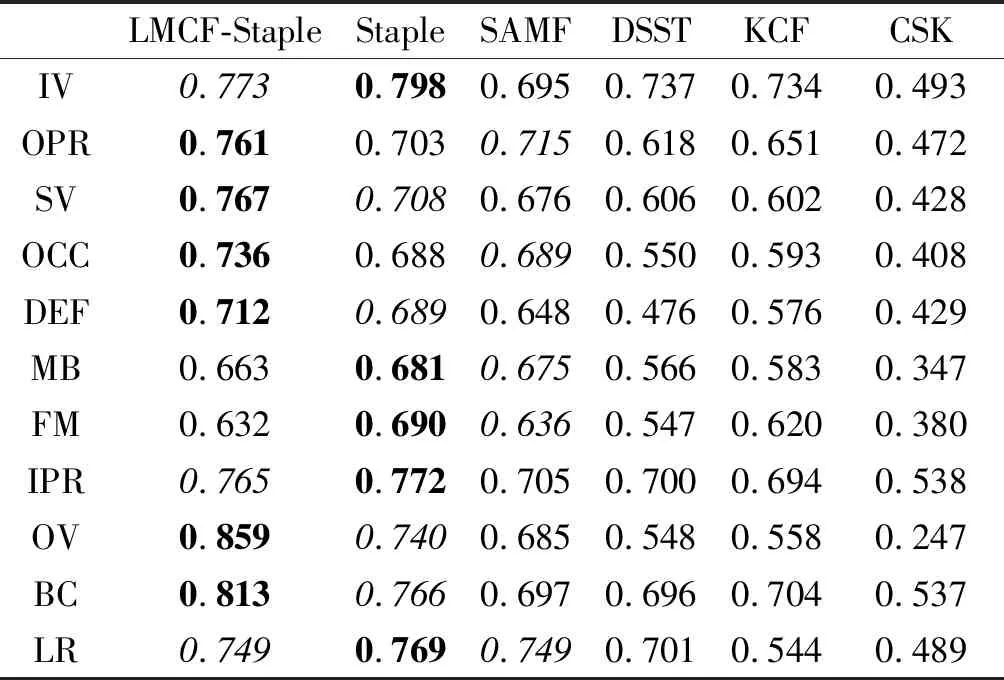
表1 OTB100 的OPE精度值表

表2 OTB100 的OPE重合阈值

LMCF-Staple算法较其他算法更优化的原因有以下几点:1.增加了直方图匹配,将前后景的相似度值计算出来,以此来影响直方图的bin值,这样就会自适应的提高算法的分辨率,表格中的数据也表明了这点;2.利用最大峰值和APCE值来约束模板的更新条件,大大降低了模板更新的不准确性,提高跟踪的稳定性和精确度;3.利用数据分析设定了合适的阈值,将原本固定的融合系数变为自适应,以此可以检测每一帧图像所需要的权重,使得算法的融合达到最优化。

4.2 OTB数据集实验测试的特定情况性能分析

选取具有代表性的9个典型视频序列进行实验的定性分析,视频序列为:Box(IV/SV/OCC/MB/IPR/OPR/OV/BC/LR)、ClifBar(SV/OCC/MB/FM/IPR/OV/BC)、Human3(SV/OCC/DEF/OPR/BC)、Liquor(IV/SV/OCC/MB/FM/OPR/OV/BC)、Panda(SV/OCC/DEF/IPR/OPR/OV/LR)、Shaking(IV/SV/IPR/OPR/BC)、Skating2_1(SV/OCC/DEF/FM/OPR)、Board(OPR/SV/MB/FM/OV/BC)、Human5(SV/OCC/DEF)。视频的跟踪效果图如图6。

图6 六种算法在九个典型视频序列上的跟踪效果图Fig.6 Tracking effect diagram of six algorithms on nine typical video sequences

Box主要是遮挡、背景杂波和尺度变化等的问题,而且在受到严重遮挡时同时伴有背景和目标极其相似的情况,在这种情况下LMCF-Staple算法和SAMF算法一直保持稳定的跟踪;ClifBar主要是在背景和目标相似的情况下快速旋转和尺度变化,此种情况下Staple、SAMF、KCF、CSK四种算法均出现漂移和最后丢失情况,而LMCF-Staple和DSST算法一直保持稳定跟踪;Human3在第54帧时出现严重遮挡并且遮挡物为白色,此种情况的噪声很难去除,但是LMCF-Staple算法仍然一直稳定的跟踪目标,而其他五种算法全部丢失;Liquor是一个具有长期跟踪的视频,在被相同颜色的瓶子遮挡以后,SAMF、CSK立刻跟丢,在被绿色瓶子再次遮挡时,DSST算法也出现丢失最后由LMCF-Staple算法、Staple算法和KCF算法跟上;Panda主要是分辨率低的情况下伴有遮挡、形变和平面内外旋转等复杂情况,最后也只有LMCF-Staple算法跟上,其他五种算法均丢失;Shanking主要是光照影响十分强烈,最后也只有LMCF-Staple算法和DSST算法平稳跟踪,CSK虽然一直试图跟上目标但是还是出现多次漂移;Skating2_1主要是在快速运动的情况下同时伴有多次遮挡、形变以及尺度变化,整个过程仅有LMCF-Staple算法一直平稳跟踪目标;Board是在超出视野情况时伴有旋转,当出现旋转时仅有LMCF-Staple、Staple两个算法平稳跟踪,其他算法漂移;Human5视频的目标距离摄像机十分远,分辨率会要求比较苛刻同时伴有相机的抖动,此种情况也只有LMCF-Staple、Staple两个算法平稳跟踪。

以上几个视频可以看出LMCF-Staple算法的综合性能远强于其他五种算法,尤其是在出现背景杂波、形变、遮挡、光照以及低分辨率情况下跟踪仍然十分稳定,而其他几种算法仅局限于尺度变化的跟踪或者颜色跟踪,尤其是在低分辨率和遮挡或者强烈的光照时就会产生跟踪不稳定,直至累计误差超出极限出现跟踪丢失。

4.3 VOT2016数据集实验测试分析

LMCF-Staple算法通过在数据集VOT2016上与当前主流的四个算法Staple、DSST、SAMF、KCF进行对比测试,数据集共60个视频序列,数据集的精度和鲁棒性精确到每一帧图像,实验得到的A-R效果图以及数据表格如下:

图7 VOT2016数据集的 A-R效果图Fig.7 Tracking effect diagram of accuracy-robustness of VOT2016 data set

表3 VOT2016A-R数据表

A-R数据表格中的鲁棒性值指的是跟踪器在测试中跟丢的次数,而不是Rs值,此处的值越小表示稳定性越好。从A-R效果图和A-R数据表格中数据得知,我们的LMCF-Staple算法的精确度和鲁棒性在原算法Staple算法基础上均有一定的提高,并且同时高于其他四种主流算法。所以,可以证明LMCF-Staple算法具有良好的跟踪性能。

5 结论

本文算法LMCF-Staple结合了LMCF和Staple两个算法,利用响应最大值和APCE值来综合约束滤波器模板的更新条件,降低了因模板不准确而继续更新模板从而导致跟踪漂移直至丢失的情况。另外,增加了直方图匹配,通过巴氏系数计算出当前帧的前景和背景的直方图相似度值,以此影响直方图的bin值,使其自适应,提高跟踪的分辨率。最后将核相关滤波器和直方图分类器的响应最大峰值、APCE值与融合响应中的系数α进行线性结合,并通过数据分析设定合适的阈值,使算法达到最优的自适应融合跟踪。LMCF-Staple算法通过在大型数据集OTB50、OTB100和VOT2016上和其他五种主流的核相关滤波器算法进行对比测试,其综合结果的精确度和成功率均为最优,稳定性也得到了一定的提高。