基于MIMO雷达的极化平滑降维酉ESPRIT算法

陈 晨 陶建锋 郑桂妹

(1. 空军工程大学研究生学院, 陕西西安 710051; 2. 空军工程大学防空反导学院, 陕西西安 710051)

1 引 言

MIMO雷达[1-2]本质上是将通信领域中的多输入多输出技术应用到雷达领域,进而和数字阵列雷达技术进行优势互补所形成的一种新型雷达。MIMO雷达由于采用了波形分集技术,和传统相控阵雷达相比,其具有抗干扰能力强、分辨率高、多目标跟踪能力强的优点,这引起了国内外研究人员的高度关注。根据收发阵元的距离,MIMO雷达可以分为两大类:集中式MIMO雷达和分布式MIMO雷达。集中式MIMO雷达收发天线各单元相距较近,主要利用波形分集和多通道相干性,进而扩展阵列虚拟孔径,提高角度分辨率和抗干扰能力。分布式MIMO雷达收发天线距离较远,每对收发天线均可以当作一组双基地雷达,利用目标回波的空间分集增益,可以提高角闪烁目标的检测性能。

本文主要研究集中式单基地MIMO雷达的波达方向(Direction-Of-Arrival, DOA)估计问题,这是雷达信号处理领域的重点与难点,广受国内外学者的关注。由于MIMO雷达具有常规阵列雷达所没有的优势(抗干扰能力强、分辨率高、多目标跟踪能力强),所以众多研究人员开始关注并研究MIMO雷达的DOA估计方法,在MIMO雷达的基础上提出了许多新的、更有效的DOA估计方法[3-15]。文献[3]提出了一种谱值优选算法,该算法抑制了目标闪烁且提高了DOA估计精度。文献[4-5]将ESPRIT算法应用到了MIMO雷达系统中,该方法可以有效地估计出信号的波达角,且运算量较小。文献[6]将MUSIC算法应用到MIMO雷达中,在一定程度上降低了算法复杂度且获得了不错的DOA估计精度,但是MUSIC算法需要进行谱峰搜索,因此该算法计算量仍然较高。针对该问题,文献[7]提出了一种基于MIMO雷达低复杂度的求根MUSIC算法,其计算量显著下降,但是DOA估计精度也随之下降。此外可以发现上述算法均假设目标是不相干的,但是在实际应用中存在大量相干目标,而最大似然估计算法可以有效的解决相干信源问题。因此文献[8-9]将最大似然估计算法应用到MIMO雷达上面,解决了相干信源问题,但最大似然估计算法需要参数搜索,算法复杂度较高,不利于现实应用。文献[10-11]将双向空间平滑算法与MIMO雷达相结合,取得了不错的解相干能力,但其解相干能力是以牺牲阵元数目为代价获得,阵列孔径有一定的损失。极化平滑算法具有解相干的能力,且不损失阵列孔径,因此文献[12]提出了一种基于MIMO雷达的极化平滑广义MUSIC算法,解决了低仰角多径相干问题,且精度较高,这表明了极化平滑算法在MIMO雷达中可以获得好的解相干能力。MIMO雷达具有波束数目较多、波束驻留时间长等特点,因此利用MIMO雷达进行DOA估计,其计算量天然的大于普通阵列雷达。针对这个问题文献[13]提出了一种降维ESPRIT算法,该算法降低了MIMO雷达导向矢量维度,进而使得MIMO雷达复杂度变低,但是该算法完全在复数域进行,没有充分利用共轭接收数据,角度估计精度有待提高。文献[14]将酉ESPRIT算法[15]应用于MIMO雷达DOA估计中,该算法利用酉矩阵对接收数据进行实值处理使其变为实数数据,且利用了共轭接收数据。

文献[16]提出了一种降维酉ESPRIT算法,该算法即降低了运算复杂度又有较高的测角精度,但该算法没有考虑相干信号源。此外,文献[13-14]中的算法均不能估计相干信源仰角,不够贴合实际。本文为了与实际需求贴合,在达到好的解相干能力的同时降低运算量,提出了一种基于极化平滑的降维酉ESPRIT算法:首先利用降维变换矩阵将接收信号数据由高维矩阵变为低维矩阵,然后利用降维后的接收信号数据构造出一个中心复共轭对称矩阵,对降维后的接收信号矩阵进行实值处理,接下来对其进行极化平滑解相干处理,最后构造出旋转不变关系式实现DOA估计。此外酉ESPRIT算法可以使数据样本加倍[14],因此本文算法可以获得更好的DOA估计精度。

2 信号模型

(1)

gp为第p个目标的极化导向矢量[17]:

(2)

式中l=1,...,L;⊗为Kron积;sp(p=1,...,P)为空间入射的P个相干窄带信号,其值为复常数,表达式为sp=αps1,p=1,...,P,αp=|αp|ejξp其幅值与相位分别代表第p个信号相对于第一个信号的幅度衰落与相位差;βp为第p个目标的复反射系数。θp表示第p个目标的波达角;Nl为匹配滤波后的高斯白噪声。

式中0≤γp<π/2和-π≤ηk<π为信号极化参数,令G=[g1,...,gP],其为极化导向矢量;φp为方位角,本文只考虑测俯仰角,所以在本文中将其视为先验信息并设其值φp=90°。发射阵列的第p个目标的空间导向矢量为:

at(θp)=[at1(θp),at2(θp),...,atM(θp)]T=
[1,e-j2πdtsin θp/λ,...,e-j2π(M-1)dtsin θp/λ]T

(3)

接收阵列的第p个目标空间导向矢量为:

ar(θp)=[ar1(θp),ar2(θp),...,arN(θp)]T=
[1,e-j2πdrsin θp/λ,...,e-j2π(N-1)drsin θp/λ]T

(4)

令

A(θ,γ,η)=[g1⊗ar(θ1)⊗at(θ1),...,gP⊗ar(θP)⊗at(θP)]

(5)

则式(1)可以简化为:

yl=A(θ,γ,η)cl+Nl

(6)

式(6)中cl=[β1s1,β2s2,...,βPsP]T。收集L个快拍的yl数据,形成矩阵Y,记为:

Y=AC+N(t)

(7)

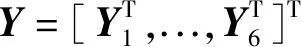
3 极化平滑降维酉ESPRIT算法

3.1 降维处理

接收阵元由K=6个分量构成,现在考虑相同极化类型的分量的输出为:

Y(k)=BG(k)C+N(k)(t)

(8)

G(k)=diag(g1(k),...gP(k))为极化导向矢量G的第k个分量,B=ar(θ)⊗at(θ);Y(k)表示MN维的接收信号矢量,把接收极化敏感阵列分解为K个子阵。

对联合导向矢量B=ar(θ)⊗at(θ)进行观察后可以发现,此导向矢量实际上是由Ne=M+N-1[12]个不同的元素线性组合而成:

B=ar(θ)⊗at(θ)=Td(θ)

(9)

d(θ)=[1,e-j2πdtsin θp/λ,...,e-j2π(Ne-1)dtsin θp/λ]T

(10)

d(θ)表示Ne×1维的虚拟均匀线阵导向矢量,变换矩阵T[12]为:

(11)

根据式(9)可以将联合导向矢量矩阵表示为:

B=TD

(12)

上式中D=[d(θ1),...,d(θP)]表示虚拟均匀线阵导向矢量矩阵,将式(12)代入式(8)中可得:

Y(k)=TDG(k)C+N(k)(t)

(13)

从上式可以看出,接收极化信号分量是由虚拟均匀线阵导向矢量D张成的高维空间,因此可以将其转换到低维空间,降低其维度。设降维变换矩阵为Ne×MN维的矩阵Q,则式(13)经过降维变换后为:

YRD(k)=QTDG(k)C+NRD(k)(t)

(14)

其中NRD(k)(t)=QN(k)(t),降维后的噪声矢量需为高斯白噪声,也即降维处理后的噪声协方差矩阵需为σ2INe,因此不难发现降维矩阵需满足该式:QQH=INe,我们可以选降维矩阵[12]为

Q=(THT)-1/2TH

(15)

将式(15)代入式(14)可得降维后的协方差矩阵为:

YRD(k)=(THT)-1/2THTDG(k)C+NRD(k)(t)=
(THT)1/2DG(k)C+NRD(k)(t)

(16)

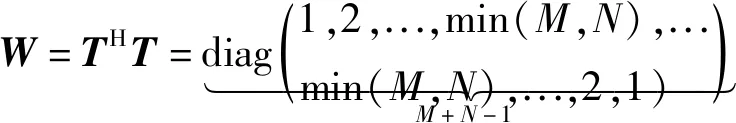
YRD(k)=W1/2DG(k)C+NRD(k)(t)

(17)

由式(17)发现接收极化信号分量经过降维处理后维度变小,且降维矩阵是稀疏的,增加计算量很小。但如果直接构造旋转不变性方程进行DOA估计,就不能充分利用共轭的观测数据。因此可以利用酉矩阵对接收数据进行实值处理来提高算法精度,此外通过实值处理还可以进一步降低算法计算量。

3.2 实值极化平滑算法

(18)

式中,ΓK[14]为稀疏的酉矩阵,其奇数与偶数维分别定义为:

(19)

经过降维实值处理后的相同极化类型分量数据为V(k),这样可以求得各个子阵的协方差矩阵为:

(20)

然后对其进行极化平滑处理,极化平滑算法[13]的本质就是对各子阵的协方差矩阵进行均匀加权求和,以恢复数据协方差的秩为满秩达到解相干的目的。下面证明降维实值后的数据经过极化平滑后的数据协方差仍然为满秩。极化平滑后的相关矩阵为:

(21)

式(21)中ΓNe为酉矩阵,因此有rank(R)=rank(RZ),RZ可以化简为下式:

(22)

式(22)中,ΠNe为K×K维的交换矩阵,因此不难得到rank(RZ)=rank(RY),RY继续化简可以得出下式:

(23)

式(23)中

(24)

设fk=G(k)C,则有式(24)可写为下式:

(25)

其中

(26)

此时当P≤K时有rank(R)=rank(RZ)=rank(RY)=rank(RK)=rank(F)=P,由此可见经过降维实值处理后再次进行极化平滑处理后可以恢复数据协方差的秩为满秩,达到解相干的效果。由理论推导和实验验证可知六维极化平滑最多可以估计六个相干信号。

3.3 ESPRIT算法

对式(21)进行特征值分解

(27)

式中,US为大特征值对应的特征矢量张成的实值子空间,也即信号实值子空间。

降维后的数据和均匀线阵接收的数据是等效的,所以可得到降维后复数域的旋转不变关系式:

J2d(θp)=ejπsin θpJ1d(θp)
J1=[INe-1,0(Ne-1)×1]
J2=[0(Ne-1)×1,INe-1]

(28)

J1,J2可分别选择d(θp)的前Ne-1行和后Ne-1行。且J2和J1满足中心对称关系

J2=ΠNe-1J1ΠNe

(29)

通过均匀线阵的中心对称关系可以将式(28)变换为实值的旋转不变关系式[15]

(30)

因此式(30)的实值旋转不变关系可以写成矩阵形式:

K2H=K1HΦ

(31)

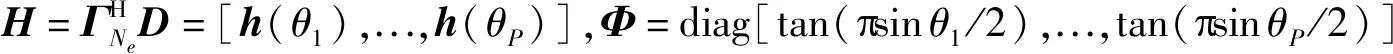
K2US=K1USψ

(32)

其中ψ=Ω-1ΦΩ,通过最小二乘或者总体最小二乘估计法求解实值矩阵Ψ,对Ψ进行实值特征值分解可以得到最终的波达角估计值。假设Ψ的第p个特征值为λp,则第p个目标的波达角可以由下式估计出:

(33)

4 计算复杂度分析

在算法实现过程中,相比于乘法运算耗费时间来说,加法运算耗费时间可忽略不计,因此本节在进行复杂度分析时,忽略掉加法运算。由文献[18]可知实数乘法计算量为复数乘法的1/4。本文算法计算复杂度主要分为三个部分:(1)降维处理;(2)实值处理;(3)特征值计算(4)特征值分解,其计算复杂度分别为:

极化ESPRIT算法计算复杂度主要分为两个部分:(1)特征值计算，(2)特征值分解,其计算量分别为:1)O(6LM4),2)M6/3,则极化ESPRIT算法复杂度为O(6LM4+M6/3)。本文在第5节对两种算法的复杂度进行了仿真,且进行了详细的分析。

5 仿真分析

本节主要通过几组仿真实验来验证本文算法的有效性与真实性。为了描述方便,将本文所提算法简称为P-RD-UESPRIT,将极化平滑算法简称为P-ESPRIT算法。

假设一个均匀线阵组成的全极化MIMO雷达。其发射阵元数和接收阵元数分别为M=8,N=6,工作频率f=3×108Hz,则波长λ=1 m,且收发阵元间距均为λ/2。假设有6个窄带相干目标信号,其波达角分别为:θ1=10°,θ2=20°,θ3=30°,θ4=40°,θ5=50°,θ6=60°。定义均方根误差(Root mean square error,RMSE)来衡量算法的估计性能:

(34)

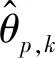
图1为本文算法极化处理后信号数据协方差特征值和未经过极化处理的数据协方差特征值点图,入射信号为六个相干窄带信号。从图1中可以看出极化处理前因为相干源的存在,使得协方差秩亏,只存在一个大特征值,而经过极化处理后,数据协方差的秩得到了恢复,存在六个大特征值,与六个相干信号源对应,达到了解相干的目的。

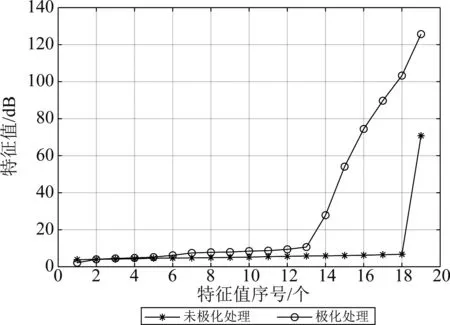
图1 特征值点图Fig.1 Eigenvalue dot plot

图2为本文所提P-RD-UESPRIT算法的波达角估计结果,蒙特卡洛试验次数K=1000,六个相干目标的信噪比均为10 dB,快拍数snap=100。由图2可以看出本文所提算法可以正确的估计出6个相干信源的波达角。

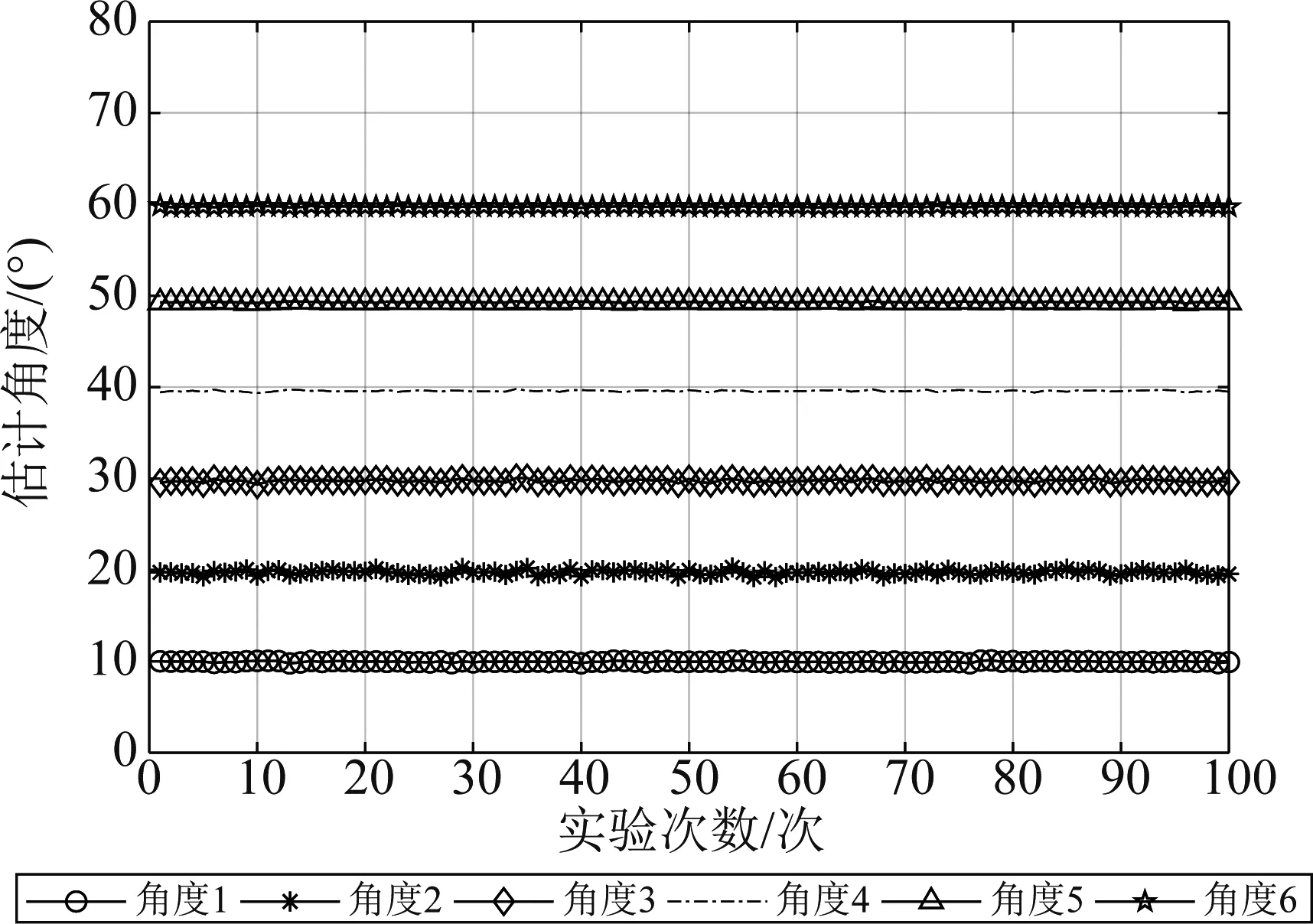
图2 六个相干目标DOA估计结果Fig.2 DOA estimation results of six coherent targets

图3为本文所提P-RD-UESPRIT算法和P-ESPRIT算法估计角度RMSE随目标信噪比变化关系(6个相干目标的信噪比相等),其中快拍数snap=100,蒙特卡洛次数K=1000。从图中可以看到本文所提P-RD-UESPRIT算法和P-ESPRIT算法估计精度都随着信噪比增大而改善,且本文所提P-RD-UESPRIT算法精度明显高于P-ESPRIT算法,这是由于本文所提P-RD-UESPRIT算法在实值处理时数据加倍。

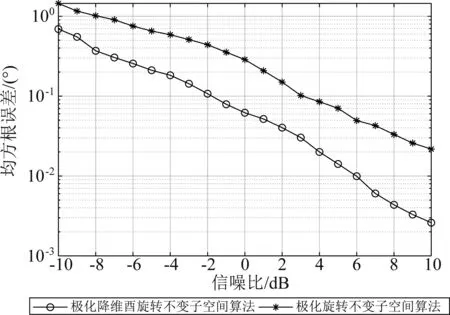
图3 DOA估计精度信噪比变化关系Fig.3 DOA estimation accuracy signal-to-noise ratio variation

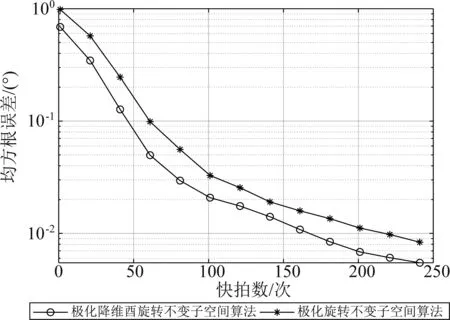
图4 DOA估计精度随快拍数变化关系Fig.4 Angle accuracy changes with the number of snapshots

图4给出了本文所提P-RD-UESPRIT算法和P-ESPRIT算法角度估计RMSE随快拍数的变化关系图,六个相干目标的信噪比均为10 dB,蒙特卡洛试验次数K=1000。从图中可以看出本文提出的P-RD-UESPRIT算法与P-ESPRIT算法相比,整体精度较高,在低快拍数的情况下P-RD-UESPRIT算法优势更为明显。

图5为本文所提P-RD-UESPRIT算法和P-ESPRIT算法的计算复杂度随阵元数目变化图,设置收发天线数目相等,即M=N,快拍数snap=100,目标个数P=6。从图5中可以看出与P-ESPRIT相比,P-RD-UESPRIT计算复杂度明显更低,且随着阵元数目的增大,P-RD-UESPRIT的计算复杂度相比P-ESPRIT将有更大的优势。

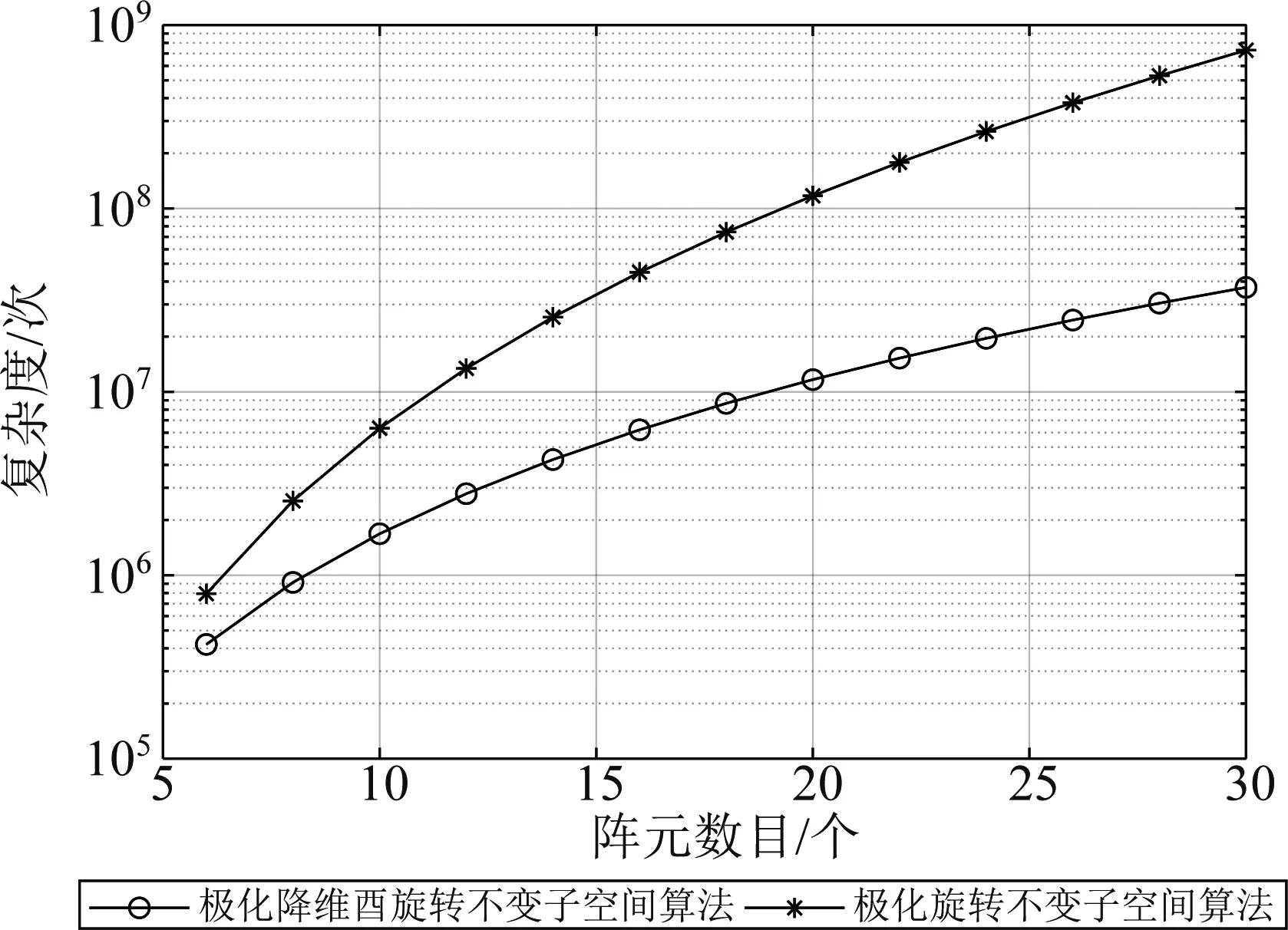
图5 复杂度随阵元数目变化关系Fig.5 The relationship between complexity and the number of array elements

6 结论

本文所提的基于极化平滑降维酉ESPRIT算法在一定程度上解决了单基地MIMO雷达相干信号DOA估计问题。该算法通过降维变换矩阵将信号接收数据由高维矩阵降为低维矩阵,然后在低维空间基础上构造中心复共轭对称矩阵,再构造出合适的酉矩阵对其进行实值处理,接着对其进行极化平滑处理以达到解相干目的,最后在解相干后的低维实值数据空间构造实值旋转不变关系式估计出信号的DOA。在理论推导部分证明了降维实值后的数据仍然可以使用极化平滑算法达到解相干的目的,且在第4节对算法复杂度进行了分析。在第5节进行了仿真实现,实验结果证明了本文算法的正确性,与常规极化平滑ESPRIT算法相比,具有更好的解相干能力、更低的运算量,且在低信噪比、低快拍数时仍然具有不错的估计精度。