基于MP-WFRFT的物理层保密增强安全方案

吴佳隆 任清华,2 李 明

(1. 空军工程大学信息与导航学院, 陕西西安 710077;2. 中国电子科技集团公司航天信息应用技术重点实验室, 河北石家庄 050081)

1 引言

由于战场无线通信网络中信道的广播特性与全域开放性,使得在消息传输的通信网络中出现一个这样的状况,即该无线网络所覆盖区域内的所有用户接收机皆可以获得该信号。而随着敌方攻击手段的不断丰富,量子计算的出现,计算能力的不断提高,战场网络的全域开放性、移动性等带来的安全风险也逐步提升。不同于密码算法在网络上层协议栈中的应用,物理层安全方法从信息论角度出发,旨在从源头上解决安全问题、实现无条件安全,可以为传统加密方案提供强力支撑,与战场网络的需求十分契合。

其中一种以无线信道互易性为基础的“信道密钥”加密方案逐渐引起了学者们的关注。根据无线信道的互易性和随机性,2000年Koorapat利用信号相位差值生成信道密钥[1];2009年,2010年Patwari N与Jana S分别给出了基于接受信号强度的密钥生成方案[2-3];2010年,Zeng K根据现有设备建立了多天线的密钥提取的实验平台[4-5]。然而,在缺乏密钥控制的场景当中,信道密钥加密方案的实施效果将大打折扣;例如利用伪随机序列的加密方案由于主要依赖于所利用的伪随机序列长度,在数据足够支撑的情况下,会呈现一种统计特性,敌方对其破解的难度也随之下降。

加权分数傅里叶变换(WFRFT)作为一种新型时频域分析手段,提出后经过多年发展已不断完善。相比于WFRFT,多参数加权分数傅里叶变换(MP-WFRFT)拥有更多加密参数,这使得信号星座的变化更加混乱,窃听方的解调将受到巨大干扰,为战场通信系统的抗截获、抗干扰特性打下基础。哈尔滨工业大学沙学军等人从多径等效出发,构建几何模型模拟WFRFT星座分裂,指出了信号叠加是造成星座裂变的原因;之后分别对经典4项MP-WFRFT中时频分量进行处理,指出时域分量对应星座分裂特性、频域分量则对应星座类噪声特性[6- 8]。空军工程大学达新宇等人通过建立几何模型,给出了星座模糊裂变与MP-WFRFT参数之间的变化关系,并在此基础上对星座模糊裂变进行了定性定量分析,成功搭建了星座预编码系统[9]。

基于以上特点,本文考虑将变换域通信手段与经典加密方法相结合,在信道密钥方案的基础上引入MP-WFRFT,提出了一种基于MP-WFRFT的物理层保密增强安全方案。通过对信号的星座实施扰乱令非合作方无法获取,在不对传输消息产生影响的前提下提升系统安全保密性能,为战场无线网络资源利用、安全防护提供了一种新方案。

2 原理分析

2.1 MP-WFRFT

MP-WFRFT是建立在经典傅里叶变换的基础上的,归一化的傅里叶变换可以定义为:

(1)

(2)

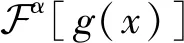
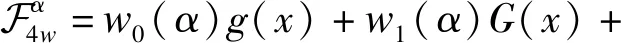
(3)

根据FRFT旋转叠加性,有:

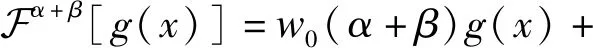
(4)

另外,基于DFT表示有:

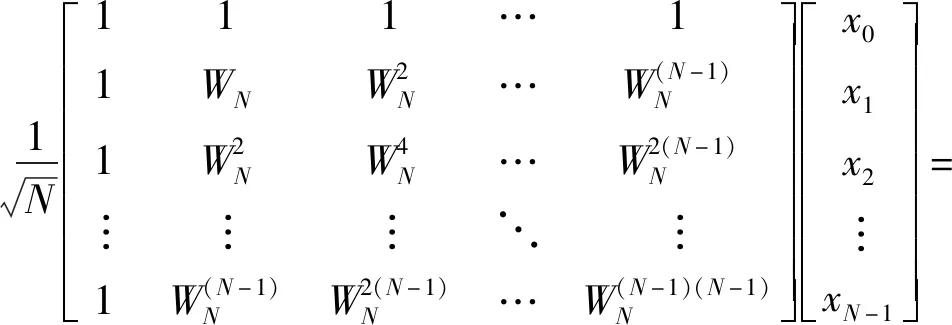
(5)

其中N表示X0(n)序列的长度;WN=exp(-i2π/N);F是DFT的变换矩阵,根据F自身性质,有F0=I,F2=P,F3=F-1,I为单位矩阵,P为移位矩阵,于是公式(3)可表示为:

(6)

可将上式描述为矩阵形式,即

ZM×1=FM×M×WM×1

(7)

其中:

同时结合FRFT的边界性,可以求得zl(α):

(8)

对z(α)进行推广后,可以得出:

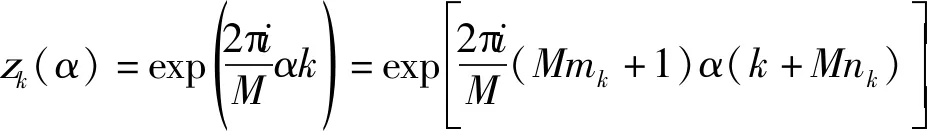
(9)

加权参数wl的多参数形式可表示为:

(10)

其中:

V=[MV,NV]

本文选取的是经典4项MP-WFRFT,一个长度为N的信息序列经过串并转换后进入4个支路分别进行处理。其中,通过w1和w3支路的信号数据在经过加权处理之前都经过了DFT模块,因而二者刚好对应于OFDM的多载波系统结构。而相对应w0和w2支路,其过程中没有经过DFT模块,对应的则是单载波系统结构,WFRFT的物理实现流程以及物理含义如图1表示。

图1 WFRFT的物理实现流程Fig.1 The physical implementation process for WFRFT

2.2 星座扰乱原理

星座扰乱方案为解决当前物理层安全问题提供了一个新的方向,通过对信号星座的扰乱,使非目的接收方无法对信号调制方式进行识别,能够提升其对传输信号窃听获取的难度。本文利用合法收发双方之间信道互相探测获取的共享密钥对信号星座扰乱过程进行控制,对相位进行随机扰乱加密,如图2所示。

图2 星座扰乱加密流程图Fig.2 The flow chart of constellation disrupts encryption

在相位扰乱过程中,假设经过调制的传统信号星座相位为θi,对第i个符号,相位扰乱序列对信息比特进行[0,2π]分割成M段,而后可以通过选择分割区域数量R则完成各时刻相位扰乱处理,则i时刻星座点xi的旋转相位可表示为:

Δθi=R*Δθ

(11)

式中,Δθ=2π/M代表信息分割后的最小分辨率,扰乱后的信号星座相位为θi+Δθi,得到信号:

(12)

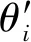
3 基于MP-WFRFT的物理层保密增强安全模型

3.1 物理层安全模型构建

根据现阶段研究,可以将TDD系统下的信道互易模型描述为图3所示。在当前互易模型下,Alice发出的下行导频信号为xDL(t),Bob接收到的信号可以表示为yDL(t),基于TDD的半双工特性,于是在τ时隙过后,Bob会发送上行导频信号xUL(t),Alice也会接收到一个信号yUL(t),于是可将Alice与Bob之间的下行信道响应描述为:

(13)

式中,Al(t)、φl(t)分别表示第l条路径的信道幅度、相位响应,τλ表示为多径时延。根据信道互易性原理,可将Alice与Bob之间的上行信道响应描述为:

(14)

于是,上、下行接收信号可表示为:

yDL(t)=xDL(t)·hDL(t)+n(t)

(15)

yUL(t)=xUL(t)·hUL(t)+n(t)

(16)

若上下行转换速率较高,可令二者间隔低于信道相干时隙,即h(t+τ)=h(t)。在信噪比提高至一定程度时,可以利用信道估计、上下行发送一致导频信号等方法令Alice与Bob获取共享信道信息。为方便后续信道估计过程,记Alice的估计载波频率与相位为fBA、φBA,Bob的估计载波频率与相位为fAB、φAB,在Bob完成上行导频信号发送之后进入发-收转换过程,转换时段为tTR,Alice完成探测信号接收之后进入收-发转换过程,转换时段为tRT,至此,完整的信号探测周期结束,进入下一迭代循环。

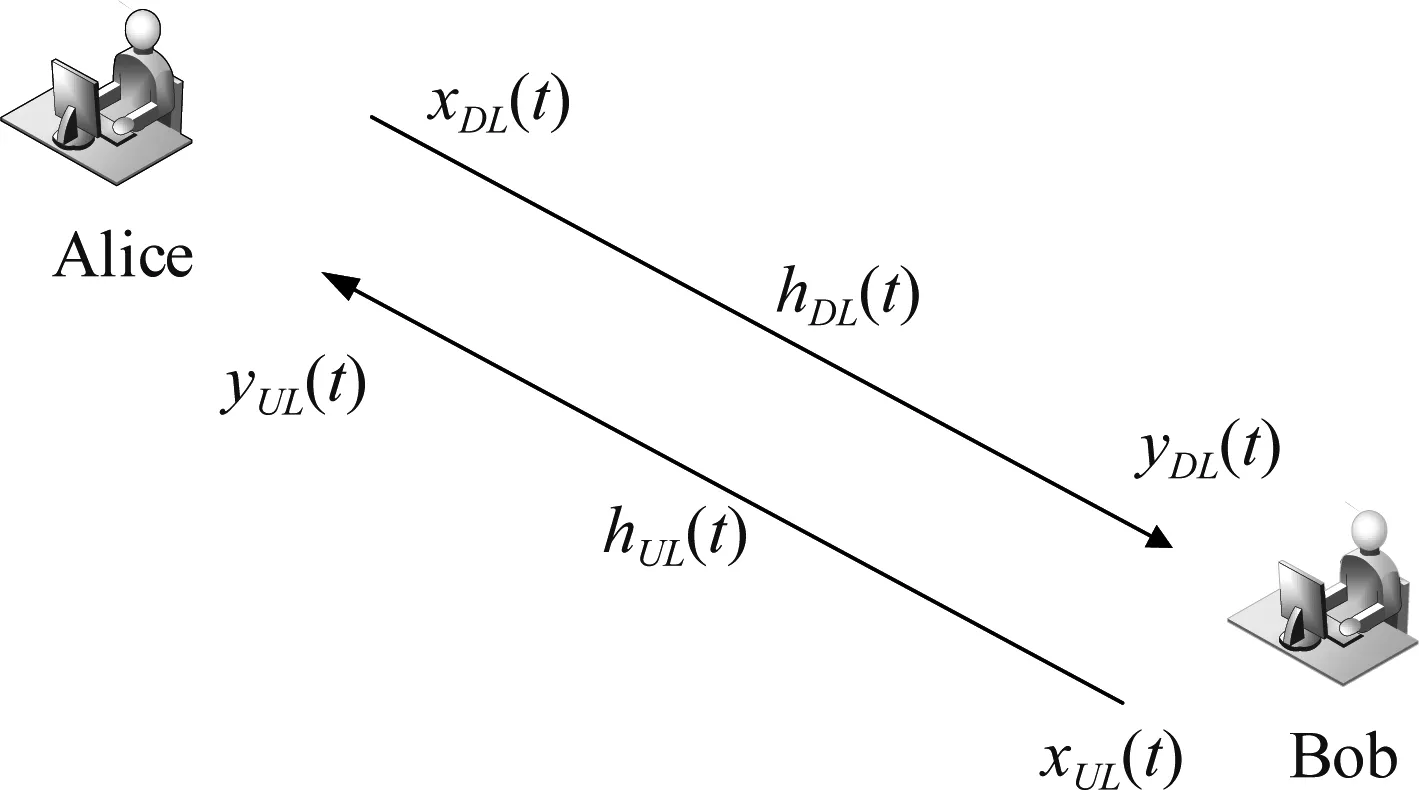
图3 TDD互易模型Fig.3 TDD reciprocal model

本文采用MMSE量化,在给定电平数J的情况下,设量化器的信号输入为x,信号输出为yk,其定义的均方量化误差可表示为:

(17)

于是,最佳判决电平可表示为:

(18)

最佳输出为:

(19)

即

(20)

可以发现在各个量化区间内MMSE量化器的量化噪声平均值为0。

在经历量化处理之后,为保证双方的密钥生成序列相同,要对二者的字符串进行纠错,通过纠错编码理论实现信息协商的过程。而后,在一致性确认模块中确认双方拥有相同的密钥,当前主要是通过Hash函数实现,如图4所示,主要流程如下:

Step 1由Bob随机选择一个信号并进行加密,此信号一般设定为一个实数R,经过Bob加密的信号表示为EKB(R),EK(·)为加密算子;

Step 2Alice利用自身密钥KA对加密信号EKB(R)进行解密,并通过Hash函数处理,再利用KA对此信号进行加密并发送至公共信道,此时的信号为EKA〈H{DKA[EKB(R)]}〉,DK(·)为解密算子,H(·)为Hash算子;

Step 3Bob利用密钥KB对信号进行解密,如果得到信号H(R),则一致性通过,向Alice送一个“Positive”的肯定信号,表明双方所拥有的密钥一致;反之,向Alice发送一个“Negative”的否定信号,表明双方所拥有的密钥不一致。

图4 密钥一致性确认流程图Fig.4 The flowchart of channel Shared key coherence validation

为了得到发送方发出的真实消息内容,用户接收机需要知晓星座置乱序列来对信号星座进行解密处理,并通过加密参数mk、nk和调制参数α的联合控制才能最终实现信号解调。实施流程如下所示:

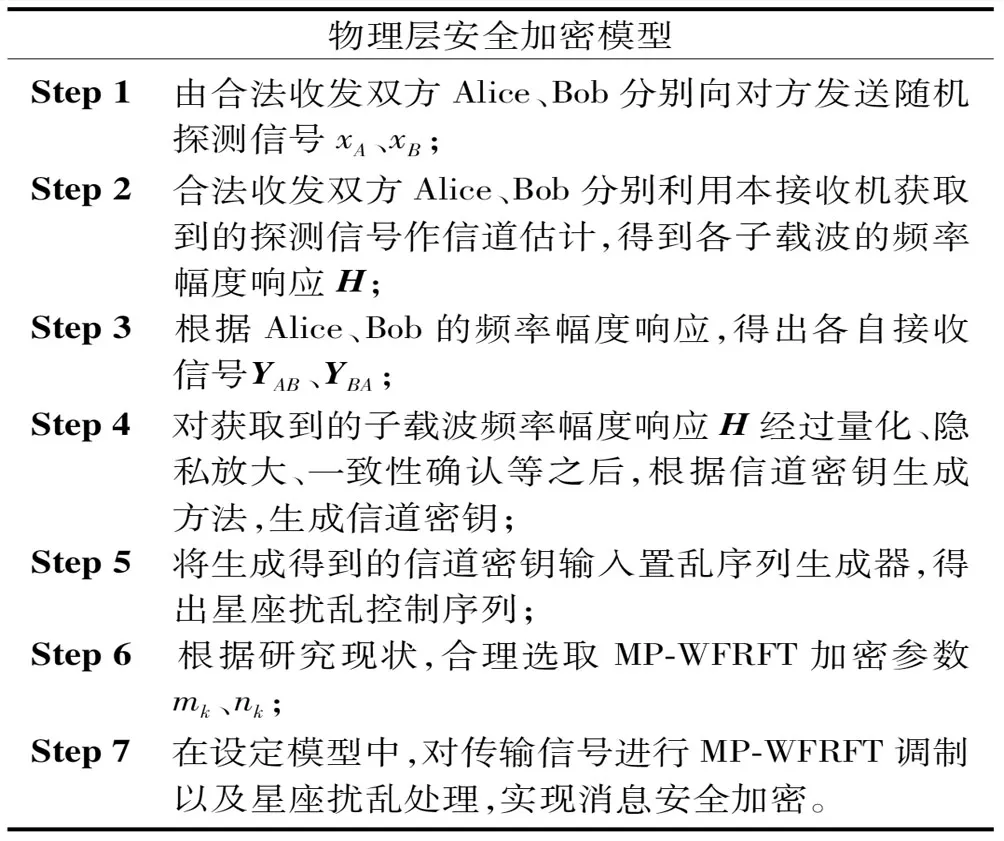
物理层安全加密模型Step 1 由合法收发双方Alice、Bob分别向对方发送随机探测信号xA、xB;Step 2 合法收发双方Alice、Bob分别利用本接收机获取到的探测信号作信道估计,得到各子载波的频率幅度响应H;Step 3 根据Alice、Bob的频率幅度响应,得出各自接收信号YAB、YBA;Step 4 对获取到的子载波频率幅度响应H经过量化、隐私放大、一致性确认等之后,根据信道密钥生成方法,生成信道密钥;Step 5 将生成得到的信道密钥输入置乱序列生成器,得出星座扰乱控制序列;Step 6 根据研究现状,合理选取MP-WFRFT加密参数mk、nk;Step 7 在设定模型中,对传输信号进行MP-WFRFT调制以及星座扰乱处理,实现消息安全加密。

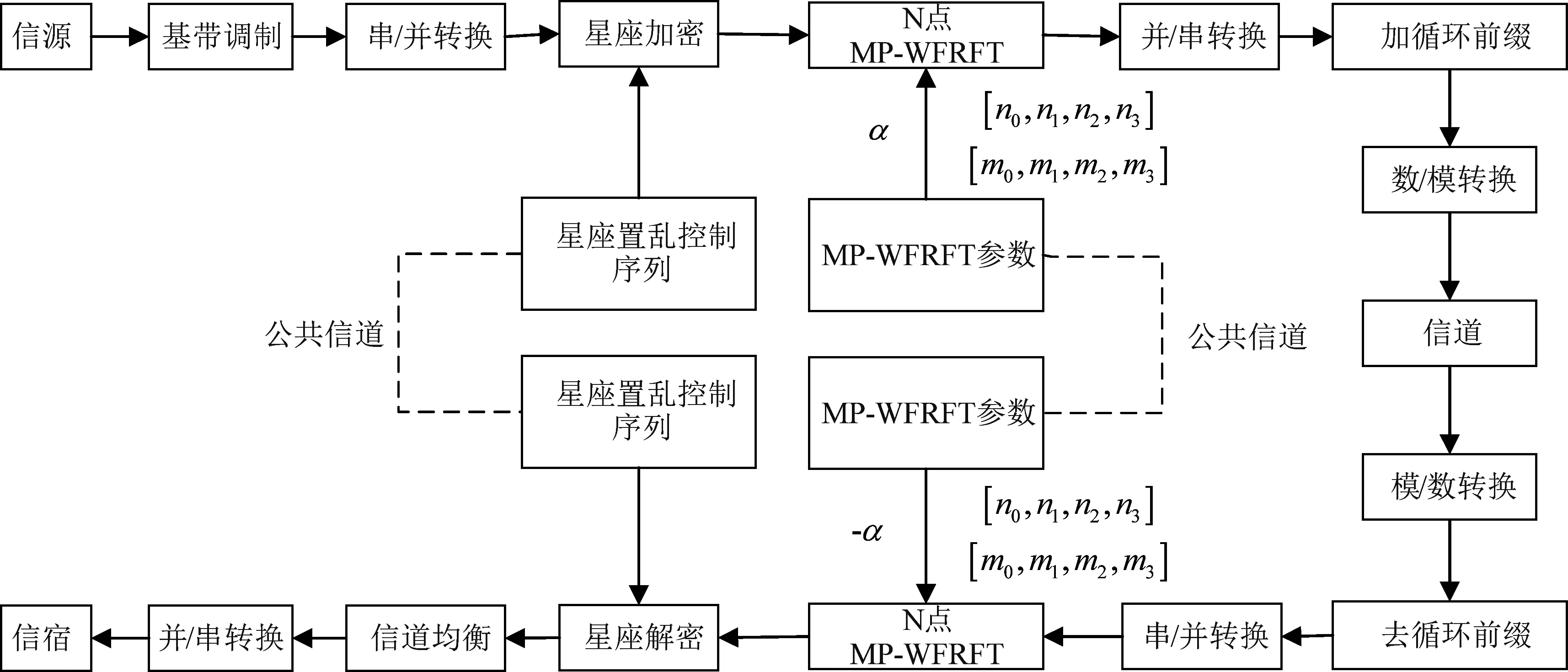
图5 系统流程图Fig.5 The flow chart of system

在以上基础上,本文构建的系统流程图可描述为如图5所示。

3.2 MP-WFRFT信号加密分析

在TDD模型下,Alice向目标方Bob发送密文,Eve试图对所传输密文进行干扰甚至截获。通信模型中,Alice向Bob发送探测信号,在接收信号过后,下一时刻Bob向Alice返送应答信号,并确定双方一致的通信密钥,在此模型下,设定互易性不对MP-WFRFT参数的选取和使用产生影响。

(21)

(22)

其中,x表示传输信号,H表示信道响应,z表示传输信道噪声,y表示接收信号。

假设合法、窃听两路信道的信道特征不相关,由于加权分数阶傅里叶变换自身兼顾单载波、多载波二者的时频特性,本文基于信道频率幅度响应生成信道密钥,并将合法传输双方Alice、Bob达成一致的信道密钥作为置乱控制序列。基于无线信道的互异性,时频域上的信道响应可近似约定为相等,本节假设合法信道和窃听信道的信道特性不相关,根据信道的幅-频响应生成信道密钥,即:

(23)

其中MA,MB,PA,PB分别为Alice、Bob的幅-频响应。

根据加密参数mk、nk和调制参数α的联合控制,信号x={x1,x2,…,xN}将被送至公共传输信道。

传输信号可以表示为:

(24)

于是,接收方获取到的信号可表示为:

(25)

同时根据WFRFT的可逆性原则,上式中的加权系数将遵循如下式约束条件:

(26)

4 基于MP-WFRFT的物理层保密增强模型性能仿真分析

本文采用多参数4项WFRFT和4096点的QPSK样本。本节通过对信号星座旋转情况的讨论,从信号自身层面分析了星座旋转的可靠性。本节根据上文的战场网络物理层安全模型,将非法窃听方分为两类:一类是窃听方无法获取合法方选取的信号调制方式和加密参数,另一类是窃听方已知信号的调制方式但无法获取调制加密参数的具体取值。下面将分别对这两类情况进行仿真研究。

4.1 针对普通窃听用户的仿真分析

为了实现战场无线网络中通信信号的隐蔽性,本节在信道感知的基础上,依据文献[10]所提出的方案,可以将调制加密参数设置为mk=[0,2,3,4],nk=[1,6,7,9]。对于无法获取信号调制方式和加密参数的窃听方,我们可以清楚地看到,由于MP-WFRFT的存在,信号经过调制之后的星座点将发生旋转偏移,频域参数加权和w1(α,V)X1+w3(α,V)X3决定了信号星座的模糊程度,时域参数加权和w0(α,V)X0+w2(α,V)X2决定了信号星座点之间的欧氏距离与点数变化,形成了调制后的星座图样。其抗截获性在此类窃听模型中发挥了较大的作用,窃听方几乎将传输的加密信号视为高斯噪声。而合法接收方可以利用双方已知的共享密钥和加密参数对信号进行解密解调,得到需要传输的真实消息内容,如图6所示。

图6 普通窃听用户接收信号星座表示Fig.6 Signal constellation representation of common eavesdropping user

4.2 针对智能窃听用户的仿真分析

同样可以将此情景下的调制加密参数设置为mk=[0,0,2,3],nk=[0,1,0,0]。对于已知信号调制方式的窃听方,我们可以清楚地看到,即使信号的调制是已知的,但由于信号星座点的旋转是依据调制参数所呈现的,在共享信道密钥加密的基础上,此时的信号星座图仍不具备原固有特性,星座点也不再固定,窃听方仍然无法正确解密信号,本节所设置方案仍然可以成功较好地提升信号的隐蔽性,如图7所示。

图7 智能窃听用户接收信号星座表示Fig.7 Signal constellation representation of intelligent eavesdropping user

本文采用误码率表达为:

(27)

图8对比了引入MP-WFRFT前后共享密钥方案的误码率性能,可以发现,在设定的复杂战场无线网络环境下,各类干扰繁多,会对用户接收机造成一定程度的影响,此场景下的无密钥方案由于受到战场网络全域开放性的影响,所传递消息将会无差别的被网络内所有中继节点接收,其误码率几乎维持在0.5附近,无法完成有效的消息传输,同时通信的安全性难以得到保障。而共享密钥方案在信噪比较小的情况下,无法满足通信安全需求标准,对信息来源的标准要求较高,无法有效适用于复杂战场无线网络。相较无密钥方案差错率极高的情况以及仅依靠共享密钥进行消息加密的方案,在同一信噪比下,本节提出的物理层安全加密方案在WFRFT的协作下能够降低系统误码率,具有优化系统性能的作用。

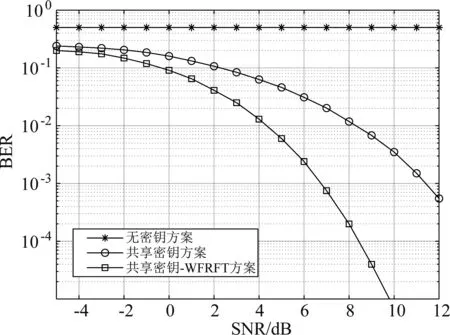
图8 不同方案下的BER性能对比Fig.8 Comparison of BER performance under different schemes

本节通过引入联合熵来度量信号星座的混淆程度,其定义可以表示为:

(28)

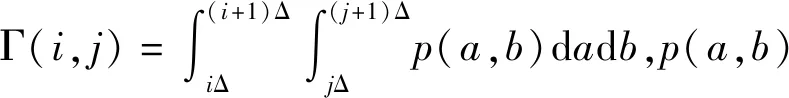
图9 信号星座图熵Fig.9 Signal constellation entropy

信号星座图熵如图9所示。可以发现,随着星座坐标量化长度的增加,信号星座的联合熵也会随之增加。将本节所提出的物理层安全方案引入共享密钥方案中,相较以往的星座图混乱程度有所增加,密文的安全性能也得以提升。信号调制方式的变化导致了信号星座图内星座点的数量与其之间的欧氏距离发生变化,近而由星座的混乱程度呈现出来。仿真结果表明,共享密钥方案中引入MP-WFRFT物理层安全方案可以显著提升星座图的混乱程度(信号星座图熵),这就表示着本节的MP-WFRFT-共享密钥物理层安全加密方案可以较好地为传输消息提供安全保证。

图10 不同情况下的BER性能对比Fig.10 Comparison of BER performance under different circumstances

图10给出了本节方案下的误码率性能,可以看出,合法接收方的误码率曲线与理论标准QPSK得出的曲线基本一致,只存在较少的偏差。对于已知传输信号调制方式的窃听方,由于选择调制参数的原则未知,在获取密文时需要对调制参数进行穷举猜测,但星座置乱控制序列的随机性以及信号较大的星座熵,使得其仍然无法实现对信号的正确解密。对无法获取合法方选取的信号调制方式和加密参数的窃听方,如果想实现信号解密,唯一的办法就是大量地增加其计算复杂度,而MP-WFRFT的引入使得该方法不再有效,消息内容的安全性能够得到保证。本节采用的共享密钥以及混合载波保密增强方式在信道响应的基础上添加了信号星座的随机旋转,因此窃听方在现有的破解手段下无法有效地对传输密文实施解密。也就是说,战场无线网络模型下的窃听者无法依靠现有的破解工具获得有用的信息,本节方案将有望实现物理层安全理论所期望达到的“完全保密”。

5 结论

针对战场无线网络中窃听用户频出的情况,为了提升传输消息在战场无线网络中的安全性能,本章节在WFRFT信号域下对信道共享密钥方案进行了研究拓展,提出了一种基于MP-WFRFT与共享密钥的保密增强物理层安全加密方案。通过合法收发双方进行相互的信道探测之后生成一个共享密钥,并在此基础上利用MP-WFRFT混合载波调制为传输密文提供保密增强。从仿真分析来看,MP-WFRFT的引入提高了信号的星座熵,这令信号星座图的混乱程度得到了较大的提升。同时对比分析了合法用户以及两类窃听用户的误码率性能,可以发现依据大计算量破解密文的手段不再有效,本章方案在信号抗截获特性上展现了良好的优越性,为战场无线通信网络的性能提升提供了一种新方案。