结合6-QAM和双层LDPC码的编码调制研究

代锁蕾 韩昌彩

(天津大学微电子学院, 天津 300072)

1 引言

融合前向纠错(Forward Error Correction, FEC)编码与高阶调制的编码调制技术可以实现更高的频谱效率和高可靠传输的误码率[1]。低密度奇偶校验(Low-Density Parity-Check, LDPC)码因其吞吐量高、错误平层低以及译码延时小等优势成为第三代FEC编码方案的候选码之一[2]。其中,多进制低密度奇偶校验(Non-Binary LDPC,NB-LDPC)码与二进制LDPC码相比,在中短码长下具有更优越的纠错性能,且易与高阶调制结合以实现更高频谱效率的传输,从而有效改善系统性能[3]。

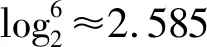
多进制LDPC码与对应阶的高阶调制结合可以实现符号级的匹配,避免比特与符号转换带来的性能损失,进一步优化误码率性能以保证信息传输的可靠性[15]。多进制LDPC码与对应阶的高阶调制结合主要分为两类,即有限域GF(2p)LDPC码与2p阶高阶调制的结合[16-18]和非2的幂次的高阶调制与对应进制的LDPC码的结合[11,19-20]。第一类采用比特交织、多级网格编码方法或者非均匀星座调制与多进制LDPC码结合的方法,将编码比特和高阶调制星座融合在一起以获得性能的优化。但随着调制阶数2p的增加,多进制LDPC码的编译码复杂度会大幅提高,导致译码时间过长,实用性较低[16]。第二类结合方法通常针对调制阶数较低的非标准QAM星座图,相应的多进制LDPC码的编译码复杂度较低。对于素数阶的编码调制,文献[11]将提出的非均匀5-QAM与7-QAM调制分别与对应进制的LDPC码编码结合,进一步提高了编码调制方案的整体性能。文献[19]提出了一种适用于卫星通信系统的7-QAM与GF(7) NB-LDPC码结合的编码调制方案,该方案将7-QAM与7进制的LDPC码结合,实现了符号级的匹配,有效地降低了对非线性失真的影响。对于非素数阶的编码调制,文献[20]提出了一种与18-QAM匹配的多级编码调制方案,该方案将1位2进制与2位3进制符号映射为1位18进制符号,将18-QAM与多级Turbo编码结合以实现匹配,但其误码率性能与基于16-QAM的编码调制方案相比仍存在0.6 dB的差距。对于3×2p进制,目前与3×2p阶调制匹配的LDPC码编码方案仍缺乏研究。

由于多进制LDPC码是二进制LDPC码在有限域GF(q)(q>2)上的扩展,有限域的阶数为素数或素数的幂[21]。因此,针对3×2p进制,难以在有限域上实现3×2p进制的LDPC码编码。针对6进制调制,提出了一种结合6-QAM与双层LDPC码的编码调制传输方案。本文采用GF(2) LDPC码与GF(3) LDPC码分层编码实现6进制编码,并在接收端迭代执行双层LDPC码的译码。提出的迭代译码方法通过GF(2) LDPC码译码信息与GF(3) LDPC码译码信息的互相传递,提高了系统的整体性能。在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下,一方面,与先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码相比,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的编码调制方案实现了一定的性能增益。另一方面,在相同的频谱效率下,执行一次整体迭代译码时,采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码时,与基于6-PSK的编码调制方案相比,结合6-QAM与双层LDPC码的编码调制方案有更优的纠错性能。随着整体迭代次数的增加,在带来一定译码延时的同时,双层LDPC码的迭代译码性能获得了有效改善。

本文其余部分的安排如下。第2节介绍了6-QAM星座图的设计方法。第3节提出了面向6-QAM的双层编码调制传输方案,介绍了发送端的双层编码调制方案以及接收端的双层迭代译码方法。仿真结果与分析在第4节中给出。最后第5节总结了本文的工作。

2 6-QAM星座图设计与分析

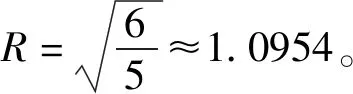
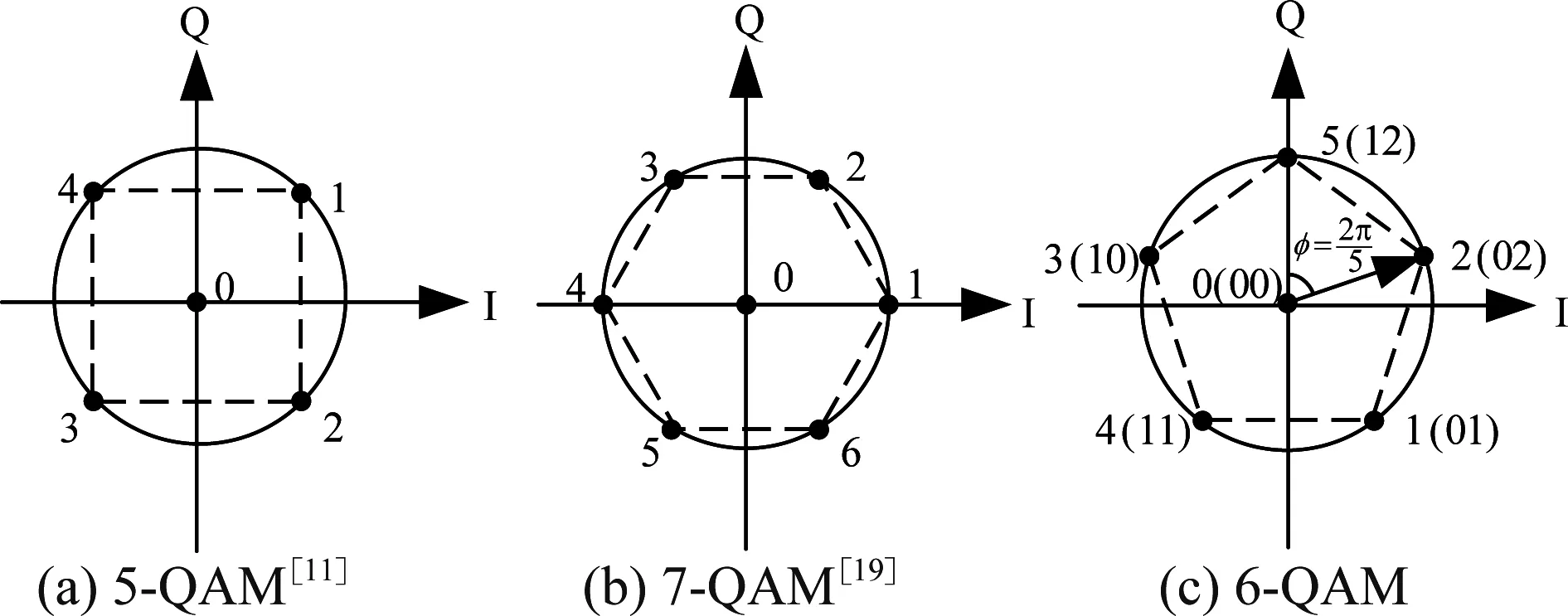
图1 星座图Fig.1 Constellation diagram

首先,由图1所示的星座图分布,可计算得到三种星座图的最小欧氏距离dmin,计算结果如表1所示。θmin表示除符号‘0’外的最小相位差,dmin的值由功率归一化后计算得到。由表1可得,6-QAM的最小欧氏距离dmin比7-QAM的最小欧氏距离高10log(1.0954/1.0801)≈0.06 dB,比5-QAM的最小欧氏距离dmin低10log(1.1180/1.0954)≈0.09 dB。因而,在相同的平均功率下,6-QAM的抗噪声性能优于7-QAM的抗噪声性能。

表1 三种星座图的基本参数

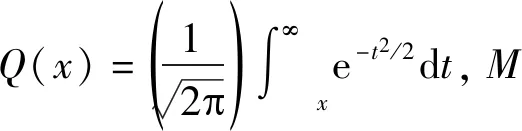
(1)

(2)

3 面向6-QAM的双层编码调制传输方案

本节首先给出了发送端基于GF(2) LDPC码与GF(3) LDPC码的分层编码方法;然后介绍了接收端双层LDPC码间的迭代译码方法。

3.1 发送端的双层编码调制方案

多进制编码阶数与高阶调制阶数匹配时,通信系统获得的译码性能最佳[11]。为实现与6-QAM匹配的多进制编码,本文提出了一种组合GF(2) LDPC码与GF(3) LDPC码的分层编码方法,两种LDPC码编码均采用基于重复累加(Repeat Accumulate, RA)结构的校验矩阵[22]。

图2给出基于6-QAM的编码调制方案发送端框图。在发送端,首先,信息序列U经过串并转换分为GF(2)信息序列UB和GF(3)信息序列UT两部分;然后,将UB和UT分别输入GF(2) LDPC码编码器和GF(3) LDPC码编码器,分层执行GF(2) LDPC码编码与GF(3) LDPC码编码,GF(2)的信息序列为UB={ub0,ub1,…,ubk-1}, GF(2) LDPC码编码所需的校验矩阵用HB表示,执行UB与HB的编码计算得到GF(2) LDPC码的码字CB={cb0,cb1,…,cbn-1}。同理,GF(3)信息序列为UT={ut0,ut1,…,utk-1},对应的校验矩阵表示为HT,执行UT与HT的编码运算,得到GF(3) LDPC码的码字CT={ct0,ct1,…,ctn-1}。进一步,按照设计的映射关系将CB与CT映射为6进制码字C;最后,将6进制码字C采用前面所述的6-QAM进行调制,调制后得到的符号序列X经噪声方差为σ2的AWGN信道传输。

图2 基于6-QAM的编码调制方案发送端框图Fig.2 The transmitter block diagram of coded modulationscheme with 6-QAM

为使相邻星座点对应的符号间具有最小的平均符号差,本文设计了如图3所示的映射规则,相邻的6进制符号之间相差一位符号。图3中第一列表示GF(2)元素即0和1,第二列表示GF(3)的元素0、1和2。6进制码字中每个6进制符号由两位符号构成,其中第一位表示GF(2) LDPC码的码字符号,第二位表示GF(3) LDPC码的码字符号。GF(2)符号与GF(3)符号的组合共有6种。这6种组合与6进制元素0～5一一对应。

图3 GF(2)、GF(3)与6进制的符号映射关系Fig.3 Mapping relationship between GF(2),GF(3) and senary symbols

3.2 接收端的双层迭代译码方法

集分割方法是编码调制方案设计的重要手段,通过将符号集合划分为更小的子集,使得子集内最小平方欧氏距离递增，从而实现更低的误码率[23]。本小节介绍了双层LDPC码间的迭代译码方法,对二进制集分割与三进制集分割方法进行了分析。

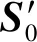
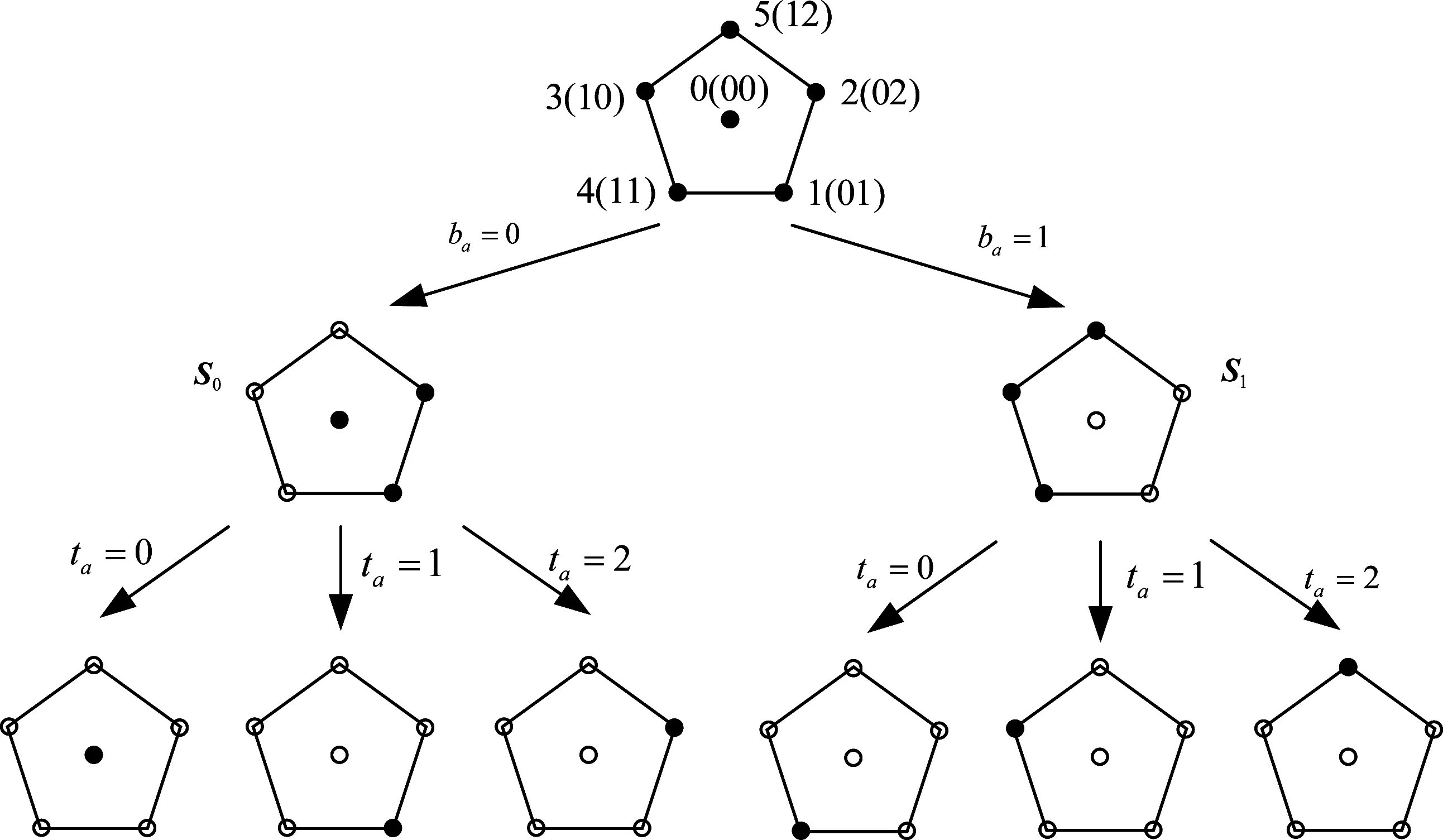
图4 6-QAM的二进制集分割示意图Fig.4 Binary set partition diagram for 6-QAM

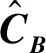
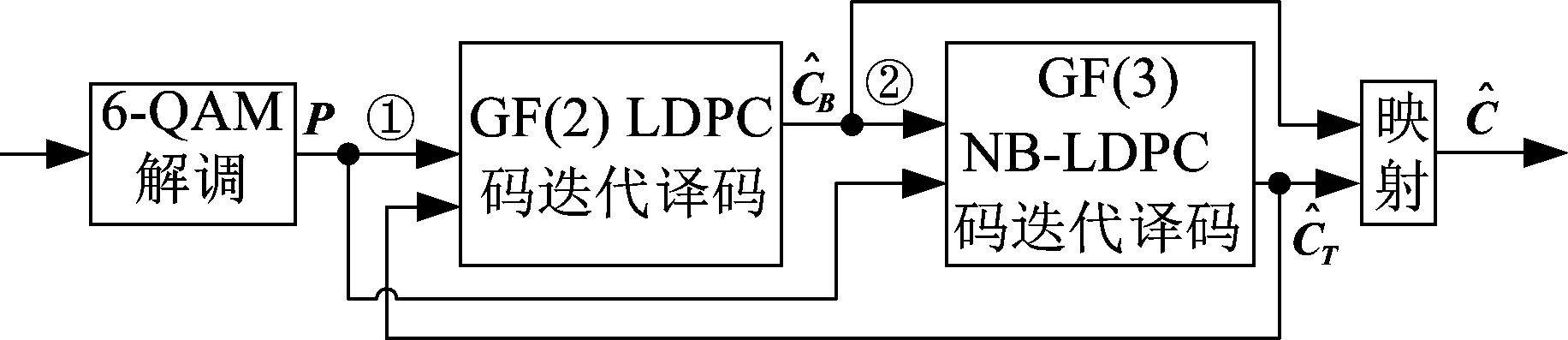
图5 基于二进制集分割的迭代译码方法框图Fig.5 Block diagram of iterative decoding method based on binary set partition

具体地,与二进制集分割对应的迭代译码方法流程图如图6所示,其中,GF(2) LDPC码译码采用对数域的置信度传播(Log-BP)算法[24],GF(3) LDPC码译码算法采用多进制BP算法[25]。GF(2) LDPC码与GF(3) LDPC码间的译码最大迭代次数表示为Iterout。GF(2) LDPC码译码最大迭代次数与GF(3) LDPC码译码最大迭代次数均表示为Iterin。具体步骤如下:

在接收端,首先,对接收到的6进制符号根据6-QAM星座图进行符号解映射, 输出符号Y的似然信息值的计算公式如式(3)所示:

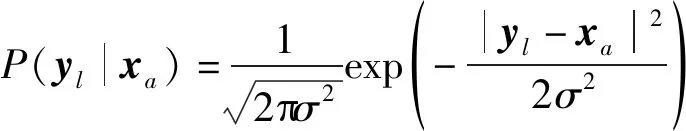
(3)

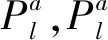
(4)

(5)

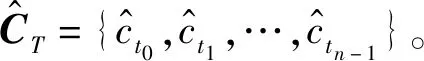
(6)

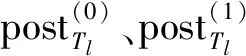
(7)

图6 基于二进制集分割的六进制码迭代译码方法流程图Fig.6 Flow chart of iterative decoding method for senary code based on binary set partition

其次,6-QAM的三进制集分割示意图如图7所示,根据ta的值将6个星座点集合S划分为三个子集S0、S1和S2。若ta=0,则子集为S0={0,3},若ta=1,则子集为S1={1,4}。若ta=2,则子集为S2={2,5}。进一步,根据ba的值将S0、S1和S2对应至6个星座点。三进制集分割后，子集S0的最小平方欧氏距离为1.2，子集S1与S2的最小平方欧氏距离均为1.6584。

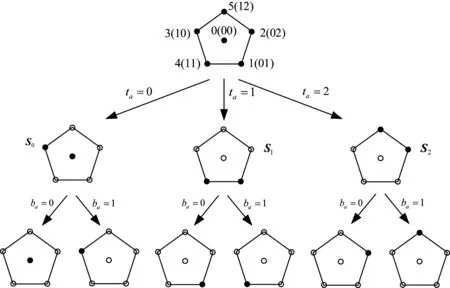
图7 6-QAM的三进制集分割示意图Fig.7 Ternary set partition diagram for 6-QAM

与三进制集分割对应的迭代译码方法先执行GF(3) LDPC码的译码后执行GF(2) LDPC码的译码,其流程具体如下,其中,GF(2) LDPC码译码和GF(3) LDPC码译码算法以及相关参数值的设置与二进制集分割对应的迭代译码方法相同,此处不再详述。在接收端,首先根据式(3)、式(4)计算接收到的6进制符号的软解调概率信息,然后执行迭代译码过程。

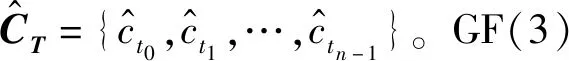
(8)

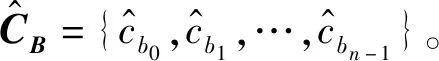
(9)

至此,完成一次双层LDPC码间的整体迭代。此时,若达到最大整体迭代次数Iterout则停止迭代,否则,继续执行GF(3) LDPC码译码。GF(3) LDPC码译码初始概率PT通过GF(2) LDPC码译码的后验概率postB与6进制符号的软解调信息计算更新。第l个3进制符号的概率更新规则如式(10)所示,

(10)

4 仿真结果

本节对提出的结合6-QAM与双层LDPC码的编码调制方案进行了性能仿真,在AWGN信道下,首先仿真了不同调制的软解调性能,其次,分析了采用不同译码顺序的双层迭代译码方法的误符号率(Symbol Error Rate, SER)性能;进一步,分别在AWGN信道下和瑞利衰落信道下,与结合6-PSK的双层LDPC码的编码调制方案以及其他进制的编码调制方案的性能进行了比较。为方便起见,先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码的迭代译码方法称为方案一,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的迭代译码方法称为方案二。作为比较的几种编码调制方案均采用相同结构的校验矩阵,LDPC码的码率均为0.5,码长为6000个对应进制的符号。如GF(5) NB-LDPC码的码长为6000个5进制符号,GF(7) NB-LDPC码的码长为6000个7进制符号。GF(5) NB-LDPC码与GF(7) NB-LDPC码译码迭代次数设置为20次。Iter表示GF(2) LDPC码与GF(3) LDPC码整体迭代的次数。GF(2) LDPC码译码的最大迭代次数与GF(3) LDPC码的最大迭代次数均设为20。

4.1 不同调制的软解调性能

本部分仿真了AWGN信道下6-QAM与5-QAM、7-QAM及6-PSK未编码时的误符号率,仿真结果如图8所示。由图8可知,6-QAM的软解调性能介于5-QAM与7-QAM之间,与理论分析一致。SER为10-5时,与7-QAM,6-PSK的解调信噪比(Signal to Noise Ratio,SNR)门限相比,6-QAM的解调SNR门限分别有0.3 dB和0.8 dB的增益。

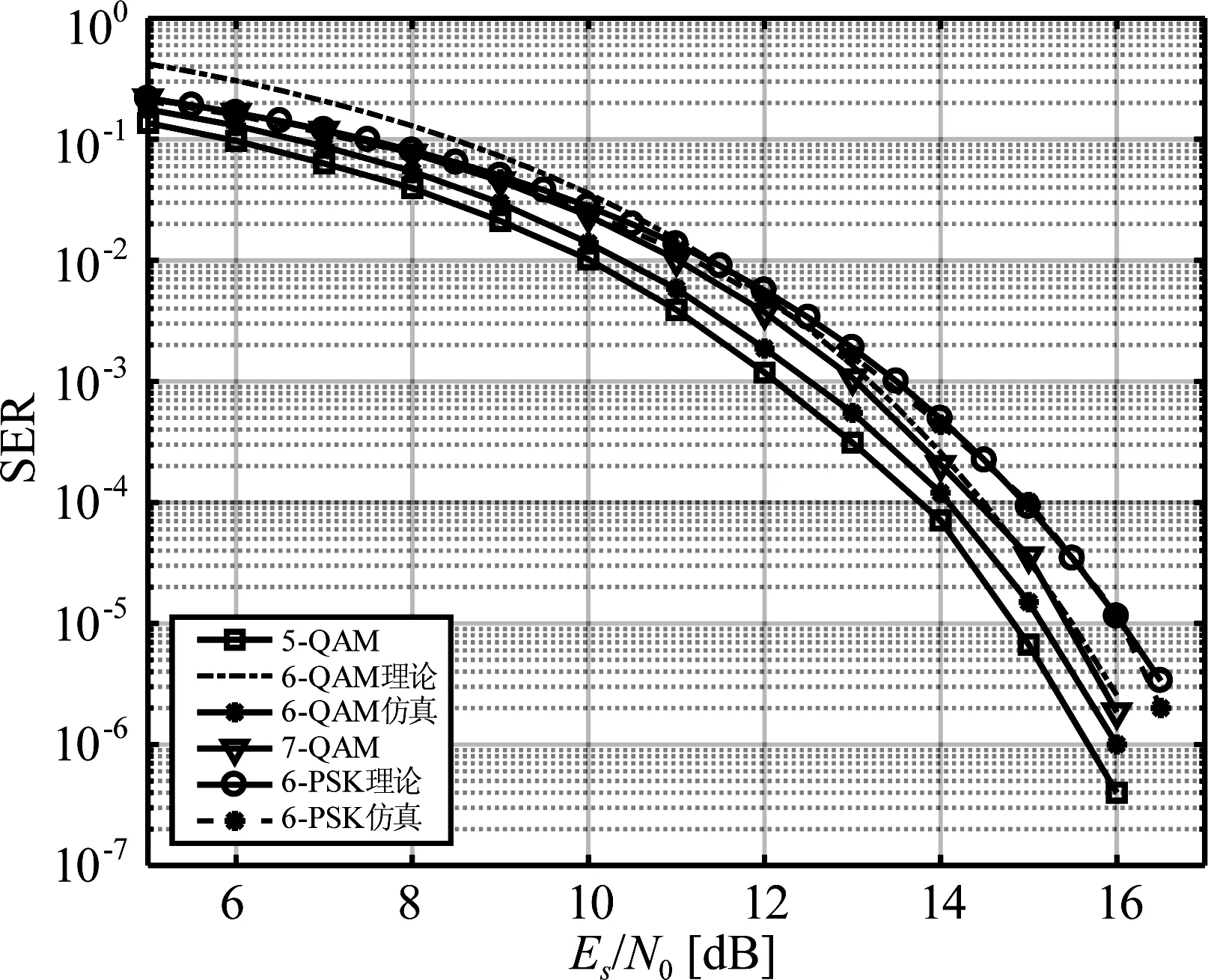
图8 AWGN信道下不同调制的误符号率性能Fig.8 SER performance of various modulations under the AWGN channel

4.2 基于6-QAM的双层LDPC码在不同译码顺序下的性能

首先,仿真验证了采用不同译码顺序时基于6-QAM的双层编码方案的SER性能。如图9所示,一方面,整体迭代次数相同时,方案二与方案一相比,获得了更大的性能增益;另一方面,随着迭代次数的增加,两种方案的误码性能均得到了进一步改善。SER为10-6时,与整体迭代1次相比,迭代2次时,方案一与方案二分别获得了0.1 dB与0.2 dB的增益。

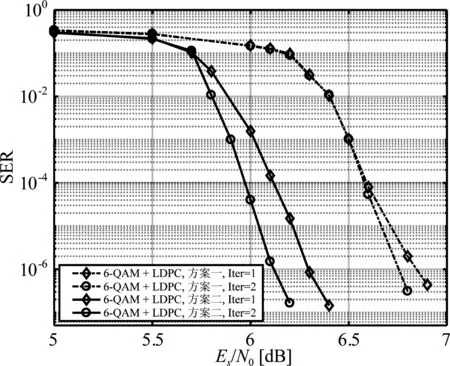
图9 基于6-QAM的双层编码调制方案的SER性能Fig.9 SER performance of two-level coded modulation schemes for 6-QAM

为进一步分析两种方案中LDPC码的纠错性能,图10给出了不同整体迭代次数下,两种编码调制方案中GF(2) LDPC码与GF(3) LDPC码的译码性能。图10中横坐标Es/N0指的是整体方案的符号信噪比。由图10可以观察到,不同的集分割方法与译码方法对纠错性能的影响较大。一方面,方案一首先执行GF(2) LDPC码的译码,方案二首先执行GF(3) LDPC码的译码,整体迭代一次时,SER为10-5时,图10(b)所示方案二中第一级GF(3) LDPC码的误码率低于图10(a)所示方案一中第一级GF(2) LDPC码的误码率,这验证了三进制集分割方法的有效性。另一方面,图10(a)中,随着迭代次数的增加,GF(2) LDPC码有较小的增益,GF(3) LDPC码几乎没有性能增益,而在图10(b)中,随着迭代次数的增加,GF(2) LDPC码与GF(3) LDPC码之间实现了译码信息的有效传递,两者的SER性能均有明显改善。因而,对于本文提出的基于6-QAM的两种编码调制方案,采用三进制集分割的方法对星座图进行划分,对应的先执行GF(3) LDPC码译码,后执行GF(2) LDPC码译码的迭代译码方法获得了更优的译码性能。

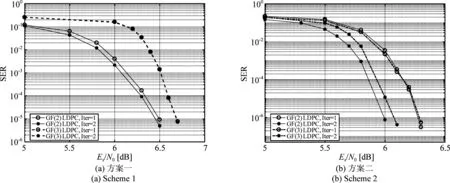
图10 GF(2) LDPC码与GF(3) LDPC码的SER性能Fig.10 SER performance of GF(2) LDPC code and GF(3) LDPC code

4.3 双层编码调制与其他方案的比较

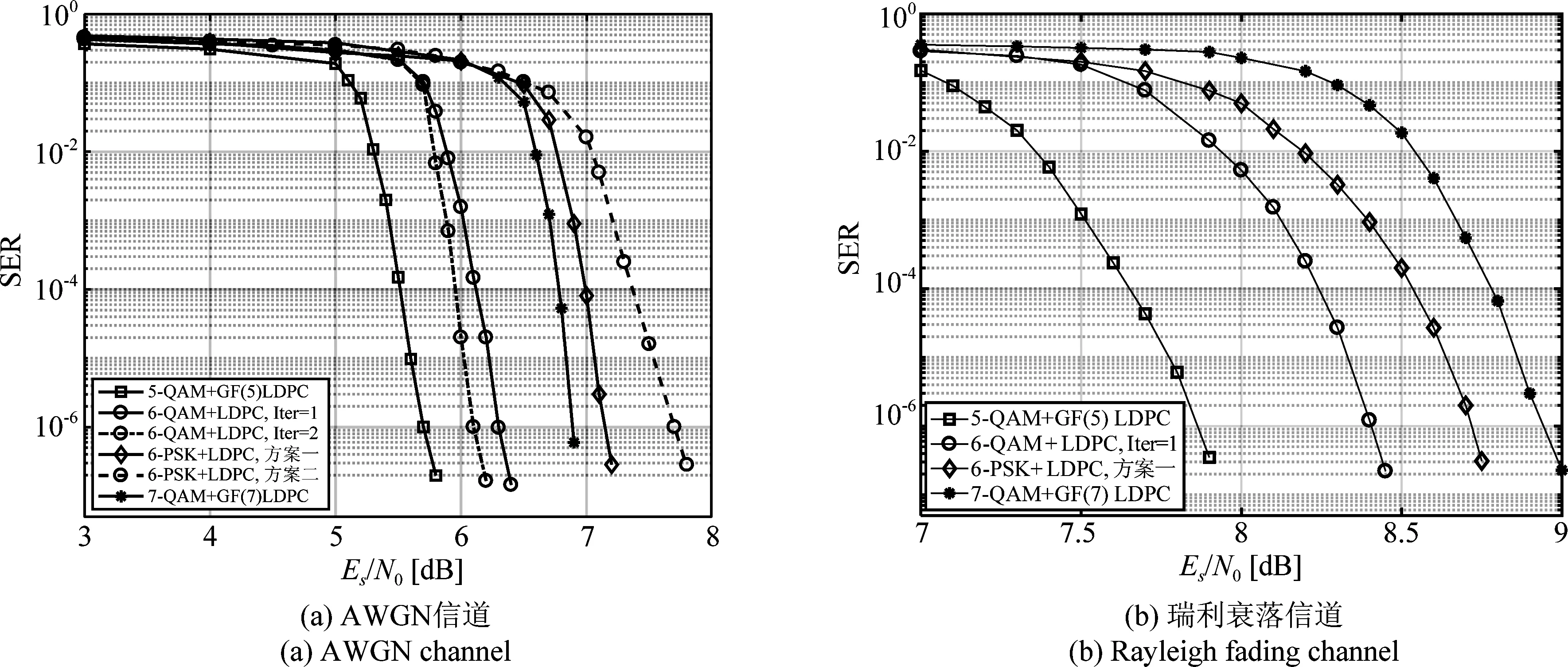
图11 不同编码调制方案的SER性能Fig.11 SER performance of different coded modulation schemes

在复杂度方面,针对基于GF(q)的不同进制的LDPC码,当译码采用多进制BP算法时,其运算复杂度为O(q2),随着进制数的增加,多进制LDPC码的译码复杂度呈指数增长[25]。但是,由于6进制不是素数或素数的幂,难以实现基于GF(q)的6进制编码[21]。因此,本文采用GF(2) LDPC码与GF(3) LDPC码组合实现双层编译码,从而实现与6进制调制的匹配。但是,双层迭代译码随着整体迭代次数的增加,在提高译码性能的同时也会增加译码复杂度,带来一定的译码延时。对于图11中基于6-PSK和6-QAM的编码调制方案,均采用双层LDPC码的编译码方法,因而二者的复杂度是相当的。综上所述,本文提出的基于双层LDPC码的编译码方法与6-QAM实现了匹配,且采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的迭代译码方法获得了更优的纠错性能。

5 结论

为实现与非标准多进制QAM调制匹配的编码,本文提出了结合6-QAM与双层LDPC码的双层编码调制传输方案,并对其SER性能进行了仿真。在发送端,通过GF(2) LDPC码与GF(3) LDPC码分层编码的方式,组合映射得到6进制码字,从而实现与6-QAM的匹配。在接收端,提出了两种针对编码调制的双层迭代译码方法,通过GF(2) LDPC码与GF(3) LDPC码之间译码信息的循环迭代,不断修正各自译码所需的概率信息,提高了译码成功的概率,进而有效改善了整体传输方案的SER性能。仿真结果表明,AWGN信道下,本文提出的基于双层LDPC码的编译码方法实现了与非标准6-QAM的匹配,采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的编码调制方案与采用先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码编码调制方案相比,获得了更优异的纠错性能。随着迭代次数的增加,提出的编码调制方案的纠错性能有进一步改善。