数控铣床误差补偿及定位精度测量研究

刘 玮

（兰州现代职业学院，甘肃 兰州 730000）

1 机床误差补偿技术

因为多种误差源的出现，都会降低数控机床的精度，为保证加工精度符合要求，往往会通过新误差来抵消之前的误差，对于机床结构的升级改善来说，此方法较为实用且经济。误差补偿技术包括硬件补偿和软件补偿两种。硬件补偿通常是在机床上外接误差补偿器或者是提升零件制造精度来实现补偿效果，具有成本费用过高、推广难度大等问题，而且如果数控系统不同，需要配备的误差补偿器的电路也不同，安装以及调试过程繁杂，适用性不高。相对硬件补偿，软件补偿是通过数控加工指令的调整来进行的，对之前的加工运动轨迹进行适当调整，实现误差补偿的效果，此方式不会改变数控机床的机械设备，仅仅调整计算机程序就可以实现，相对方便和简单，具有较为明显的优势。

2 数控铣床定位误差检测与定量分析

所谓数控铣床定位误差，指的是在制造以及装备铣床传动设备过程中出现的误差导致的铣床运动不准确，误差会影响加工零件原本的精度。分析并归类定位误差，可以较为直观的总结影响各种误差的最关键的因素。本文主要从重复定位误差、位移误差以及反向间隙等层面来对定位误差情况进行讨论。

2.1 数控铣床进给系统

本文主要以某机床厂的MvcBSOB 型三轴立式数控铣床为分析对象。MvcBSOB 型铣床使用的操作系统为FANUC Series Oi Mate-MODEL D，相关的参数包括：工作台面的长与宽是l050mmx500mm，主轴箱在Z 轴行程是550mm，工作台在X 轴的行程是800mm，主轴中心距离立柱导轨面550mm，滑台在Y 轴的行程是500mm，工作台面距离主轴端面是105mm～655mm，切削给进速度最大是10000mm/分，快速给进速度最大值是X 轴-16m/分、Y 轴-米/分、Z 轴12m/分。如下图是给进系统的主体结构图。

图1 MVC850B 型号机床给进系统主体结构图

2.2 数控铣床的定位误差测量

对MVC850B 出现的定位误差进行测量，一般测量起点是零点，对X 轴和Y 轴两个方向的行程中的线性定位误差展开测量。第一，在电脑测量软件中对相关测量参数进行设置，确定目标位置，Y 轴（0mm～500mm）或者是X 轴（0mm～800mm），间距选择为50mm，进行等距测量。第二，按照机床运行程序，来在计算机上选择相关的测量参数，通常为双向测量+线性定位方法，其中过冲量和暂停周期的参数，都是机床程序中参数值的0.5 倍。

2.3 数控铣床定位误差分析

为对验证误差展开分析，应该对铣床使用后的定位误差变化进行对比和讨论。本文所用的MVC850B 型数控铣床，在一开始的定位误差测量时，因为机床比较新，无太大的磨。在该机床持续使用一年以后，再次对其定位误差展开测量，对比结果如下图所示。图中的N-r 以及N-f 代表使用1 年后机床的反向和正向进给运动误差，而B-r 以及B-f 代表未使用前的反向和正向误差。

按照测量结果，如果定位误差大于零，说明实际值高于理论值，如果定位误差小于零，说明实际值低于理论值。分析上图2/3 的测量结果发现，在一年以后，不管是X 轴还是Y 轴，都不体现周期规律，而是以线性规律为主。由此可见，在使用铣床过程中，导轨受到了磨损，导致导轨存在的周期性误差不再有，是的直线度误差增加，作用到机床自身的定位误差上，导致机床定位误差增加。

图3 MVC850B 型数控铣床一年前后Y 轴方向误差对比

3 数控铣床定位误差补偿试验

测量结果是否贴合实际，决定着是否能科学补偿定位误差，另外，数据样本的可靠度也影响着误差补偿的精度和效率。本文在前面对定位误差因素、误差测量以及测量结果进行了分析，为后续定位精度的提升、加工误差的降低奠定了一定的基础。本次将在前面定位误差分析、测量以及结果讨论的前提下，探讨一种以坐标系偏移为基础的误差补偿综合方法，重点对与定位误差和反向误差展开补偿，最终来尽可能保证机床的定位精度。

反向间隙补偿思路。反向间隙一般在不同运动轴上，轴与轴互相间无太大影响，如果轴自身的运动方向出现变化，就会有反向间隙。因为零件装备方法不同和不同位置的丝杆磨损差异，不同位置的反向间隙也有所不同，因此应该讲机床各个轴的行程分段。

X 轴和Y 轴平面中刀具编程的运动轨迹，理论上是从P0 点运动到P5 点，因为不同轴的反向间隙互不影响，因此假设只有X 轴的运动方向出现变化，Y 轴运动方向不变。如果x 轴上i 点的位置为xi，那么xi的反向间隙值为δ(xi)。刀具编程在理论上的运动轨 迹 方 向 是：M0 →M1 →M2 →M3 →M4 →M5。因为反向间隙作用， 实际的运动过程是：M0 →M1 →M2 →M'2 →M'3 →M'4 →M'4n →M5。进行反向间隙补偿以后， 路径又变成了：M0 →M1 →M2c →M3c →M4c →M4 →M5，如此一来，就能够还原到理论运动轨迹上，实现了间隙补偿。

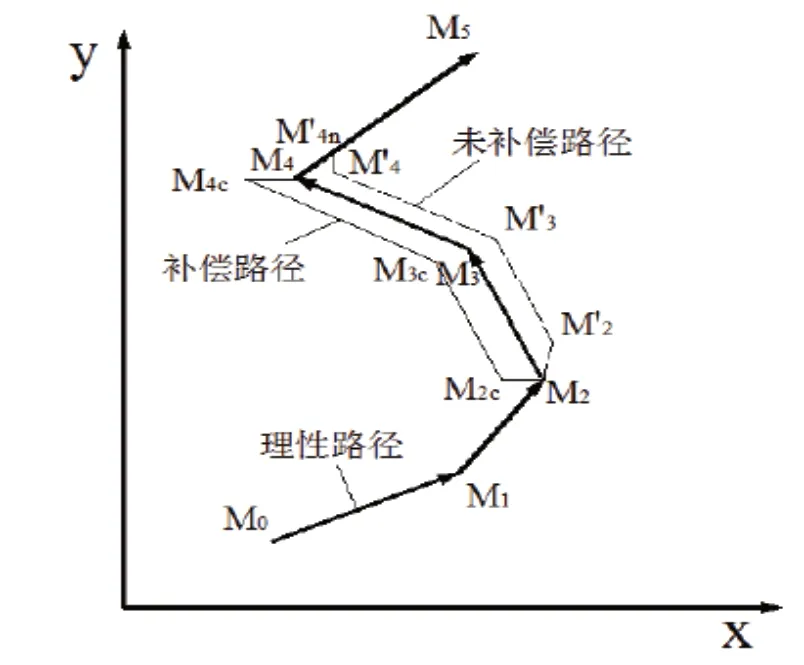
图4 反向间隙补偿运动轨迹演示

按照上图所演示的，加工过程中，铣床轴的运动包括下面四种不同情况：

第 一 种：xi+1＞=xi，并 且xi＜=xi-1，运 动 轨 迹 为M3 →M4 →M5

第 二 种：xi+1＞=xi，并 且xi＞=xi-1，运 动 轨 迹 为M0 →M1 →M2

第 三 种：xi+1＜=xi，并 且xi＜=xi-1，运 动 轨 迹 为M2 →M3 →M4

第 四 种：xi+1＜=xi，并 且xi＞=xi-1，运 动 轨 迹 为M1 →M2 →M3

如果在X 轴方向上的某一点i 上，铣床运动方向出现变化，反向间隙是δ(xi)，就会发生第一种和第四种方向，然后展开反向误差的补偿。

4 结束语

讨论分析数控铣床定位误差补偿以及测量过程的准确性，能够保证定位误差的有效补偿，然而因为测量仪器等相关条件有限，本文只研究了静态情况下的补偿和检测。未来数控铣床势必会更高水平、高效能发展，需更深入分析并探讨误差补偿技术，研究出可以以误差测量数值为前提，进行数控指令直接调整的误差补偿程序，从而促使数控铣床的作业效率、精准度更高，更符合要求。