多通道感应同步器高精度融合及其FPGA实现

李太平 姜 林 陈伟男 夏振涛 胡继宝

（上海卫星装备研究所，上海200240）

1 引言

感应同步器作为一种电磁传感元件，结构上的多极设计可以很好地匀化加工过程中单极机械误差，最终提高系统的测量精度。同时，感应同步器工作原理完全依赖电磁耦合，具有寿命长、可靠性高、抗污染、耐高低温等一系列优点，被广泛地应用于航天、航空等领域。

针对感应同步器的工作特点，邱子峰等设计了基于DSP 和AVR 的测角系统，但是对于DSP或者AVR 来说，由于感应同步器的解算模块各不相同，没有形成统一的标准，所以没有标准的外设可用。在使用DSP 或者AVR 控制计算模块时，需要用IO 接口模拟，占用了DSP 或者AVR 有限的IO资源。刘丽艳等此方面也进行了深入的研究。

在角度融合方面，上海技术物理研究所做了大量的工作，在融合算法中，采用了七段式融合的方法，最终精度满足了使用要求。文献［7］中，结合解算单元的跟踪原理，推导了粗精通道，以及每个通道的sin、cos 和ref 信号之间的幅值和相位关系要求，为了高精度解算和融合提供了理论支撑。

本文主要设计一套高性能的角度跟踪系统，介绍了系统的硬件设计，重点描述了硬件系统设计、基于谐波注入的角度融合算法和该算法在FPGA 中的实现，最终获得感应同步器的高精度融合绝对角度。试验结果表明，该角度融合系统可以很好的抑制外界干扰，融合精度优于1.22 ×10°，提高了系统的测量精度，满足航天任务的需要。

2 硬件系统设计

如图1所示，相对于文献［3］中采用COM 口与上位机通讯的方式，该硬件系统直接采用JTAG 口与上位机通讯。在FPGA 内嵌入逻辑分析仪，上位机中使用ChipScope 与FPGA 通讯，既可以降低开发周期，同时也可以充分利用逻辑分析仪中提供的各类触发机制，实现对片内信号的高速跟踪，而不需要受限于COM 口的传输速率。

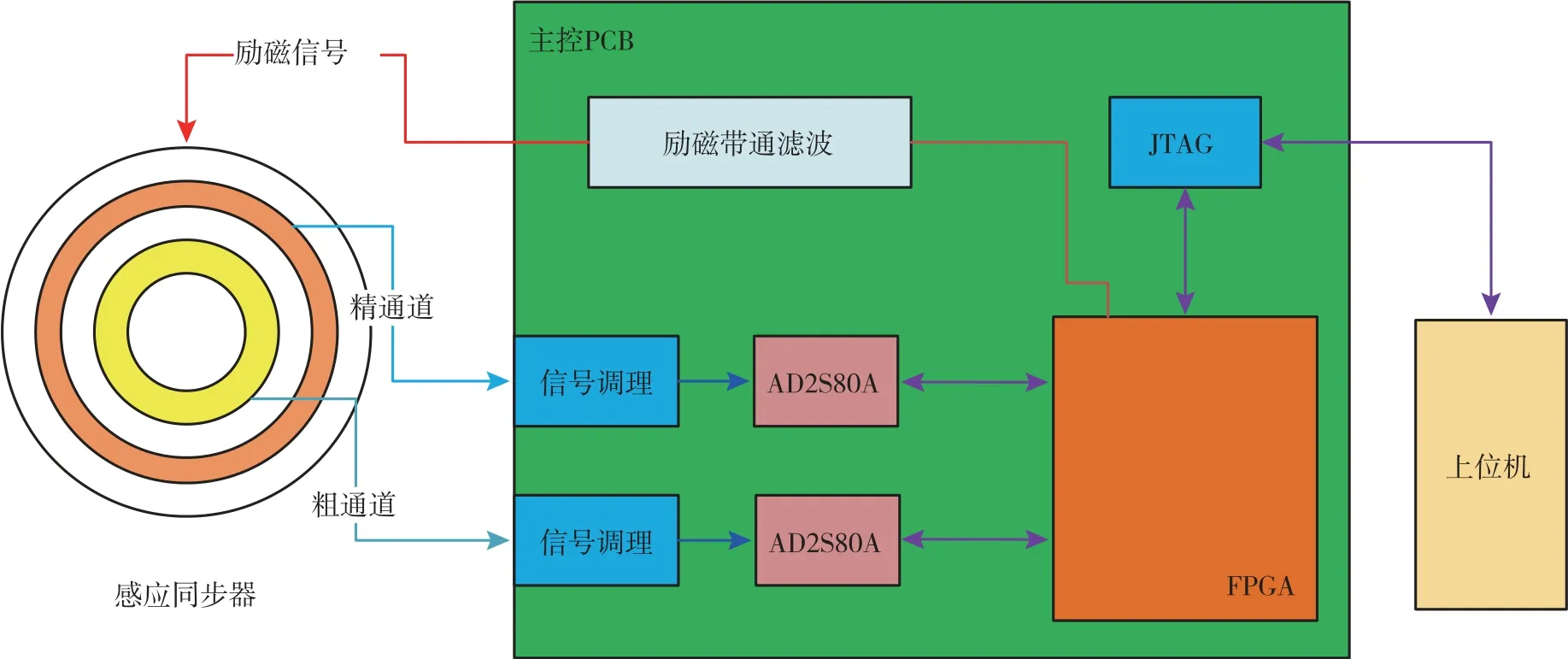
图1 感应同步器测角系统Fig.1 Inductive synchronizer angle measuring system

2.1 励磁电路

感应同步器采用交流信号励磁，在一些精度要求不高的场合可以直接使用方波励磁，方波的占空比是根据励磁信号的等效幅值确定的。但是，这种方波励磁方法会带来比较大的谐波分量，造成系统的测量精度降低，难以满足本系统的测量精度要求，所以本系统仍然采用传统的正弦波励磁。为了减少元器件的数量，降低电路硬件系统设计的复杂程度，同时提高FPGA 的利用率，励磁信号采用了SPWM + 带通滤波器的方式生成。该励磁信号直接由FPGA 片上生成，SPWM 波的参数如表1所示。

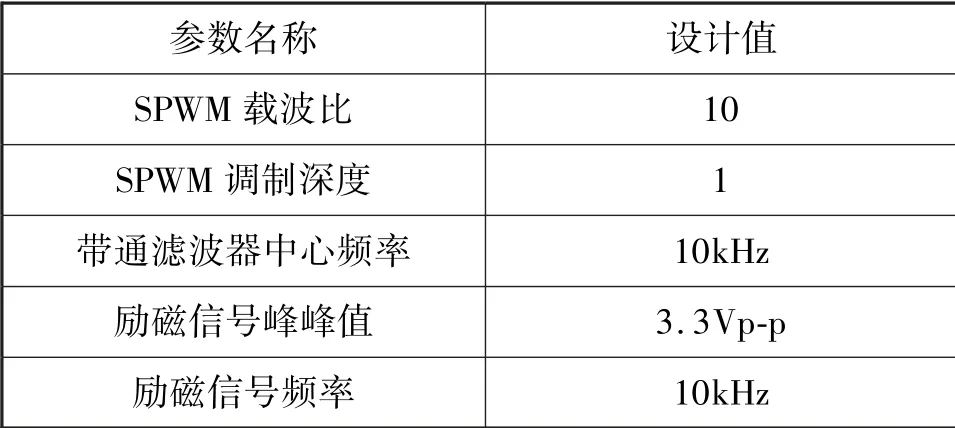
表1 正弦励磁信号设计值Tab.1 Sinusoidal excitation parameters

SPWM 生成的励磁信号为变脉宽的方波，滤波转换为正弦波后再接入功率运算放大器，功率运算放大器采用OPA548 实现，驱动电流限制在500mA，最终驱动感应同步器。SPWM 波和滤波后激励正弦波如图2所示。

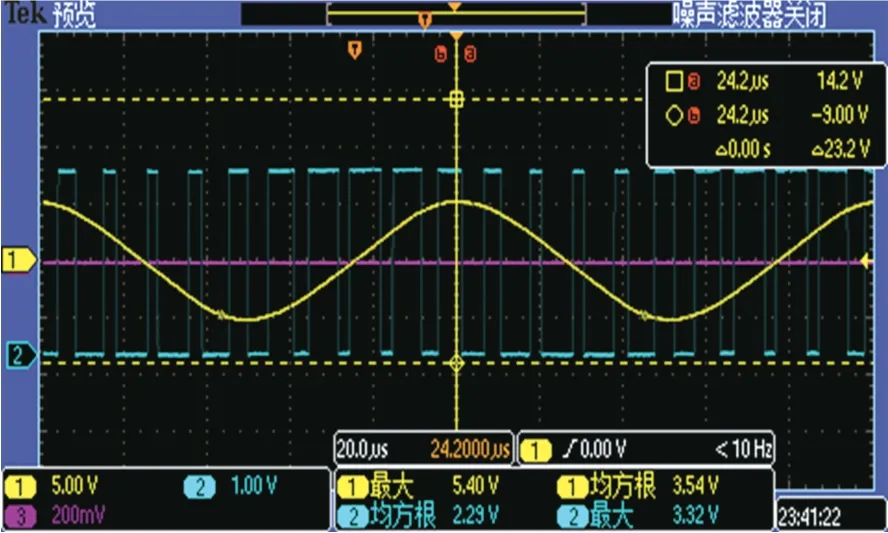
图2 SPWM 波与滤波后正弦励磁信号Fig.2 SPWM and filtered sinusoidal excitation

对于滤波模块，采用一级带通滤波器和一级低通滤波器串联的形式实现。其中带通滤波器设计如图3所示。

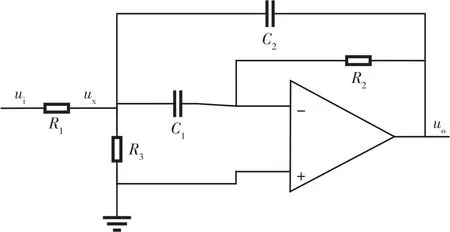
图3 带通滤波器Fig.3 Band pass filter

假设输入为

u

，输出端为

u

，

R

和

R

连接点处的电压为

u

，则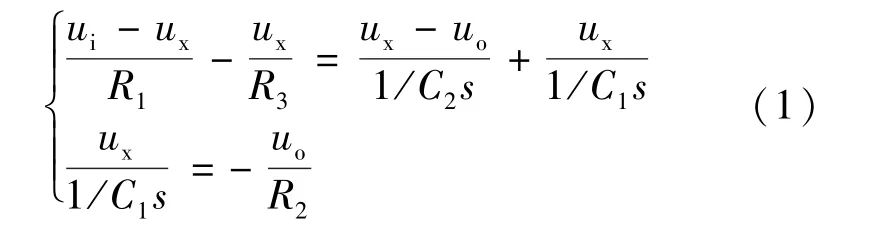

可以求得传递函数为

取

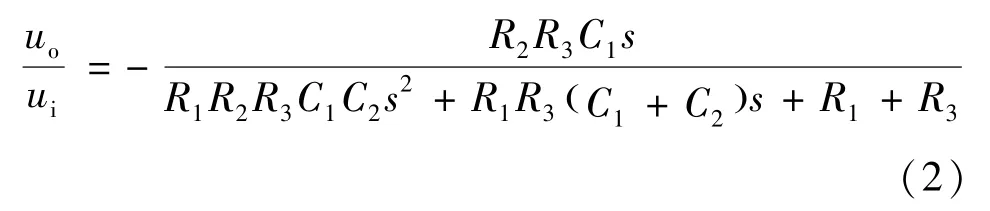
R

＝21kΩ、

R

＝42.2kΩ、

R

＝8.45kΩ、

C

＝1.0nF、

C

＝1.0nF，系统bode 图如图4所示。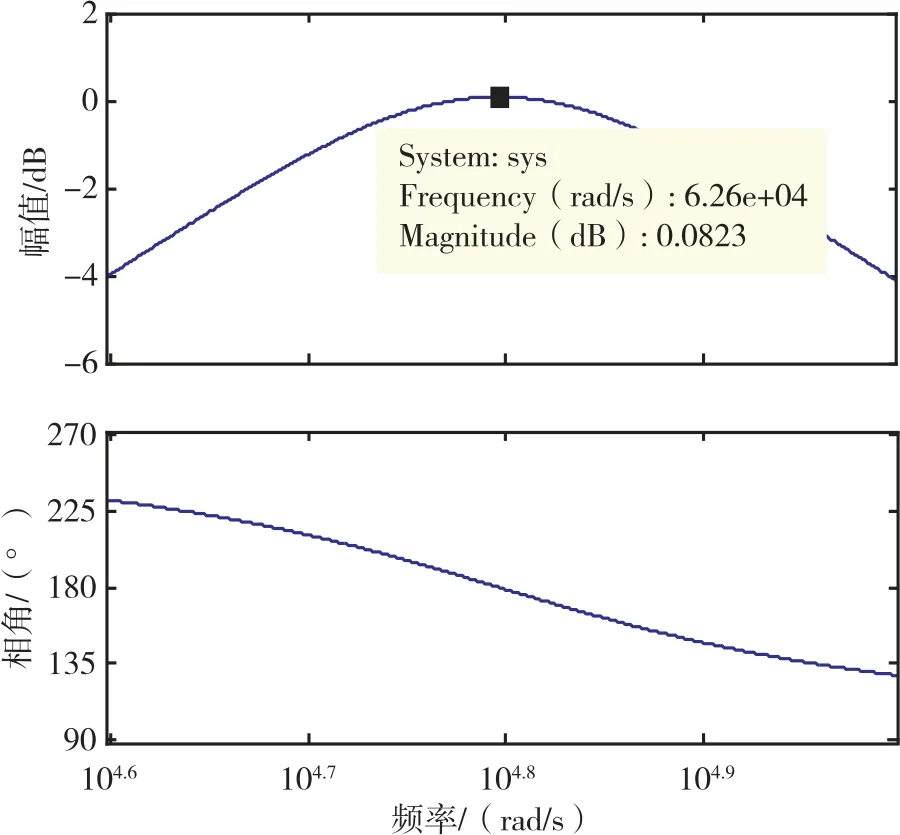

图4 带通滤波器bode 图Fig.4 Band pass filter bode diagram

2.2 感应同步器角度采集

在励磁信号的周期激励下，感应同步器的sin、cos 端输出与励磁频率一致的正弦波，但是信号低于2mV，为了满足后端解算的需要，需要经过图1中的信号调理模块进行处理，最终到达解算模块的波形如图5所示。图5 中1、2 和3 通道对应的分别为sin、cos 和ref 信号的实测波形。

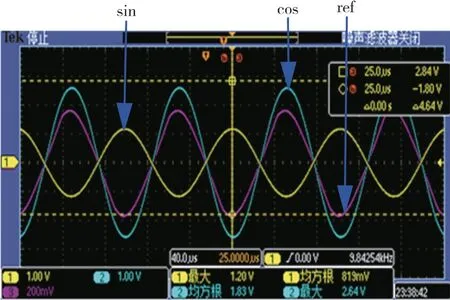
图5 单通道sin、cos 和ref 信号Fig.5 Single channel sin／cos／ref signals

信号调理模块主要包括一级差分放大，一级带通、一级低通和一级全通移相放大器。差分放大主要为了提高系统的输入阻抗，降低输出阻抗，同时提供一个较大的初级放大倍数。带通和低通是为了滤除不必要的频率分量，全通移相可以确保最终输出端sin、cos 和ref 信号之间经过前级放大移相之后，仍然满足特定的相位关系。由于差分放大器的通带很宽，所以在感应同步器的工作频率内，差分放大模块只放大信号的幅值，而不影响系统的中心频率，所以在调节过程中，在完成了带通和低通的调节之后，可以再次调节差分放大电路的放大倍数，以确保sin、cos 端输出信号的一致性。差分运算放大器选择采用INA128。

根据文献［7］，为了提高系统的测量精度，sin、cos 和ref 信号之间相位和幅值之间需要满足特定的关系，根据系统精度设计如表2所示。

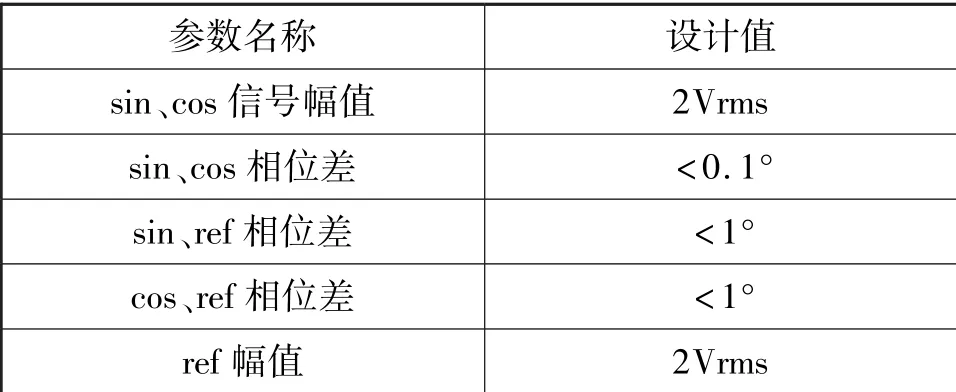
表2 sin、cos 与ref 信号设计值Tab.2 Parameters of sin／cos／ref signals

将感应同步器输出的sin、cos 信号以及ref 信号经过信号调理之后，接入AD2S80A 中，即可实现角度的测量。测量的位宽和跟踪角速度与图6所示的外围电路的具体参数有关。

对于AD2S80A 的具体配置，相关的手册配置非常详细，在均有介绍，本文不再赘述。需要说明的是，AD2S80A 的内部跟踪原理为锁相环跟踪，对于多极感应同步器，如多通道感应同步器的精通道，其最大跟踪角速度为电气角速度，等于机械角速度与极对数的乘积，在配置图6所示的外围电路时，需要考虑极对数对电气角速度的放大效应。

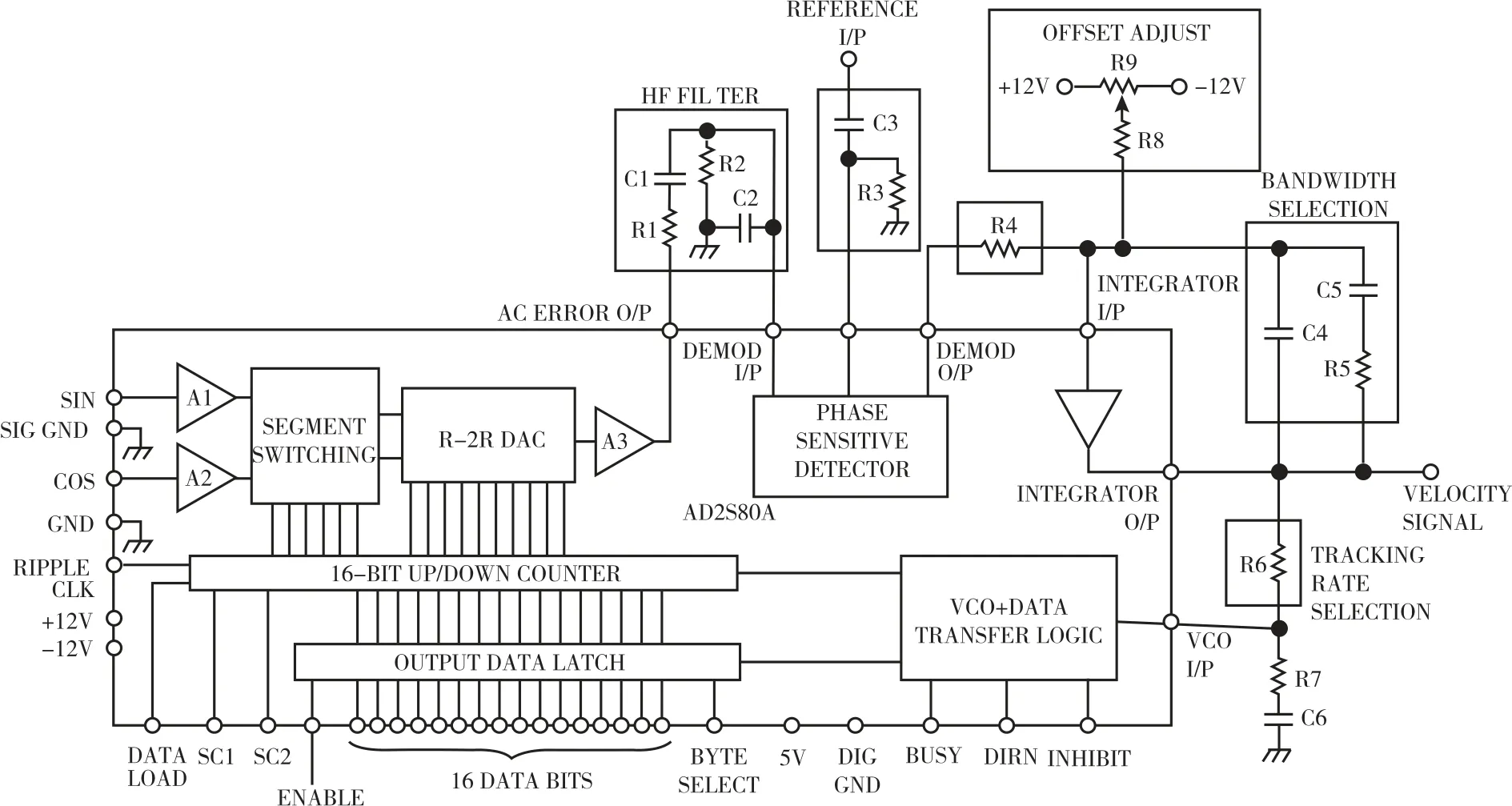
图6 AD2S80A 外围电路Fig.6 AD2S80A peripheral circuit

3 谐波注入融合

由于AD2S80A 的最高量化位数只有16 bits，一般稳态时最高也只能实现14 bits。对应360°的工作范围，量化精度只有1.3，难以满足高精度的需求。所以需要对感应同步器的粗精通道数据进行融合，以提高测量精度。

根据多通道感应同步器粗精通道的极对数，可得：

式中：

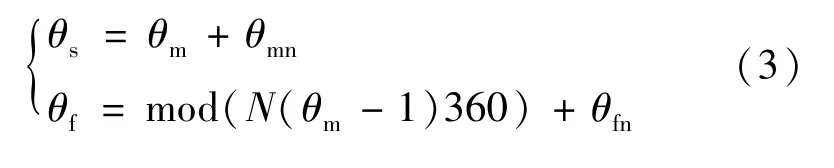
θ

——电机的实际机械转角；

θ

、

θ

——分别为粗通道、精通道角度输出数据；

θ

、

θ

——分别为粗通道、精通道角度的测量误差，

θ

主要来源于感应同步器设计、安装误差，

θ

主要来源于制造误差，为小量；

N

——精通道的极对数。所以，当

N

＝180，忽略

θ

，可得：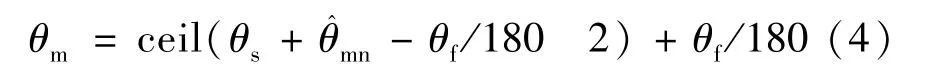

所以当

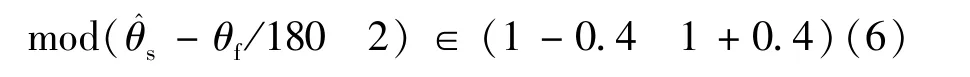
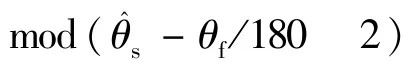
图7 校正前后粗精通道角度差Fig.7 Coarse and fine channels angle difference before and after correction

4 FPGA实现

4.1 粗通道数据矫正

4.1.1 正弦值计算

根据公式（7）的融合算法，需要进行1、2、4 次谐波的正弦值计算。虽然Xilinx 提供了可以进行实时计算正余弦值的IP 核，但是这种方法需要占用大量的FPGA 资源。所以在满足精度的前提下，为了节约FPGA 的LUT 资源，充分利用片上RAM，正弦值采用查表的方法获得。

如图8所示，利用Xilinx 提供的IP 核Distributed Memory Generator，生成一个深度为128，宽度为12 bits 的ROM。ROM 采用.coe 文件进行初始化，保存128 个的正弦值，其中第

n

个数据为sin（（

n

-1） ×90°/128）。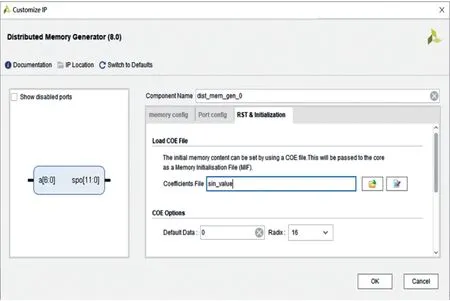

图8 正弦表Fig.8 Sine Table

对于公式（7）中的加法和乘法，由于三角函数和角度值的循环性，可以直接进行加法、乘法运算，而不需要考虑数据溢出的问题。

以求解sin

α

为例，说明公式（7）各项正弦值的计算。假设

α

用16 位数据表示，最高位为

α

［15］，最低位为

α

［0］，图8 中输入地址为

a

［6：0］，输出数据为

d

［11：0］，正弦值用13 位的有符号数表示，则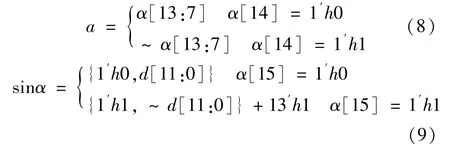

其中，公式（8）、（9）中的运算符～表示按位取反，｛｝表示位拼接运算，

xhy

表示一个长度为

x

位，用16 进制表示为

y

的一个数据，

h

表示为16 进制。

4.1.2 高精度数据融合

为了实现粗精通道的数据融合，根据公式（4）需要计算

θ

／

180。

θ

的量化位数为16 位，0°对应于16

h

0，360°对应于17

h

10000，所以

θ

／

180 可以直接进行移位运算，而不需要进行额外的除法。

θ

的最大取值为360°，如果

θ

用角度制定点数表示，需要的整数部分最短只需要8 位，则

θ

／

180 可以表示为将其二进制数据右移7 位，即为其角度制。对于公式（4）的取整运算，

θ

的量化位数为16位，0°对应于16

h

0，360°对应于17

h

10000，所以计算角度的过程可以表示为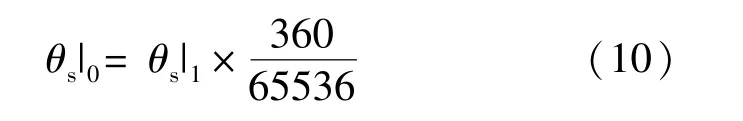

其中，

θ

｜表示

θ

的角度制表示，

θ

｜表示

θ

的二进制表示，1LSB ＝360°/65536。为了复用计算

A

sin（

θ

+

ψ

）过程中的乘法IP核，根据公式（9），sin

α

为13 位的有符号数，所以公式（10）中，360/65536 也表示为13 位的有符号数，为了提高乘法精度，选择小数的部分尽可能长，选择小数部分为19 位，即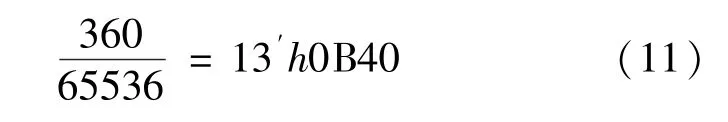

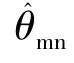
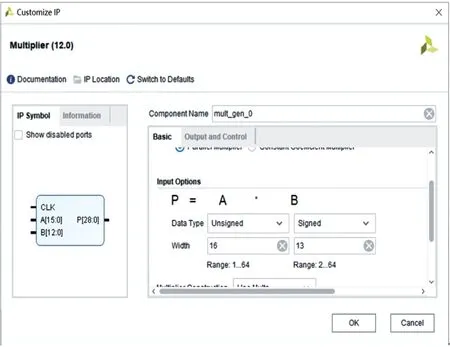
图9 乘法器IPFig.9 Multiplier IP

将公式（11）代入公式（10），即可求得

θ

，结合

θ

/180 的移位运算，最终代入公式（4），即可求得感应同步器的实际机械转角位置。

4.2 试验结果

融合之后，FPGA 内的逻辑分析仪实时监测，将电机旋转到任意位置后，自测角度未发生跳变，ILA 中的trigger 信号未触发，自测精度优于2 位，即1.22×10°。

5 结束语

根据绝对式感应同步器的测角原理，设计了感应同步器的励磁电路和信号调理电路，通过配置转换模块的外围电路，实现了对角度的稳态跟踪测量，提出了谐波注入的方法，进行了数据融合，并在FPGA 内进行了实现和试验验证。结果表明，该测角系统具有很强的抗干扰能力，自测精度优于1.22 ×10°。该测角系统具有很强的通用性，同时，在FPGA 内实现时，使用的IP 均为基础IP，整个系统具有很强的可移植性，对于其他设计具有一定的参考意义。