露天控制爆破振动对邻近建筑物影响的分析*

2021-04-17雷兴海吴桂义雷振贺路

采矿技术 2021年2期

雷兴海，吴桂义，雷振，贺路

(1.贵州大学，贵州贵阳 550025；2.贵州理工学院，贵州贵阳 550025)

0 引言

随着我国经济的快速发展，城市化进程正在快速推进，我国许多城市都在进行大量基础设施建设，城区的扩展以及住宅区的新建，都要对城市周围的岩土进行开挖，目前，开挖岩石最有效、最经济、最便捷的施工方法是爆破，爆破振动作为爆破过程中最大的灾害效应，引起了众多学者对爆破振动的研究。

受到土地资源的限制，我国城市建筑物的主要特点表现为高耸密集，露天岩土爆破开挖时，爆破振动波通过岩体传播到周围的建筑物地基中，再由建筑物地基传播到建筑物，建筑物在爆破振动波的作用下产生明显的动力效应。当振动效应超过建筑物允许的最大安全效应，就会引起建筑物的破坏[1]。

雷振等[2]通过爆破振动现场测试，分析了爆破地震波作用下高层建筑结构振动传播规律，得出爆破地震波作用下测点的垂向振动速度恒大于切向和径向振动速度；随着距爆源高差的增加，爆破振动速度逐渐增大；随着距爆源水平距离的增加，爆破振动速度逐渐减小。谢承煜等[3]采用爆破振动信号测试系统对爆破振动进行实时监测，同时运用动力有限元数值分析方法分析，指出改变露天爆破的起爆顺序以及爆破方向，对于降低爆破振动可以获得良好的效果。刘美山等[4]通过对爆破试验的各项测试结果进行分析，对比类似工程的经验，提出了小湾水电站高边坡开挖的爆破安全判据，并确定了使用原则，其试验成果在施工爆破中得到了验证。陈至昊和杜建伟[5]根据现场实际参数，利用ANSYS/LS－DYNA 软件进行模拟分析，研究发现三矢量振速峰值随楼层升高逐渐降低，直到接近建筑物的顶部时发生局部放大效应，三矢量位移值随楼层升高逐渐增加，与振速峰值规律相反。研究结果对城市轨道建设中的爆破施工与监测以及相应减振技术具有一定的参考和借鉴意义。张玉琦等[6]通过现场爆破试验及振动测试，分析基坑开挖爆破振动对建筑物结构的影响；根据高层建筑爆破振动安全控制标准，提出了基坑开挖爆破最大单段控制药量。

祝文化等[7]采用现场实测的爆破振动信号，对邻近爆区的厂房结构进行分析。建筑物的高度对爆破质点振动速度和位移具有明显的放大作用，而且速度放大效应比位移放大效应大，并确定了由高度差引起的放大系数。

综上所述，由于爆破的复杂性，不同的地质条件下，爆破振动对建筑物的影响是大不相同的，因此，针对贵阳市某爆破工程的地质条件和临近建筑物，进行了相对应的研究分析，得出与此相符合的爆破振动传播规律，为工程的设计和施工提供准确的指导。

1 爆破现场测试

1.1 工程概况

某爆破场地位于贵州省贵阳市某山体和一密集居民小区，小区由高度为60 m建筑组成，建筑物与爆破场地之间有一条双向 8车道的城区主干道，日常车流量较大。爆破开挖采用2号岩石乳化炸药。由于爆破场地对面是高层建筑小区，采用了控制爆破，并对其进行了实时监控。高边坡主要为中硬岩石，采用深孔控制爆破和逐孔起爆的方法进行开挖，爆破参数见表1。

表1 爆破参数

1.2 试验仪器

试验仪器为 NUBOX-8016爆破测振仪，包含TP3V-4.5三维速度型传感器5只，专用信号线缆5根。NUBOX-8016是一款采用全新技术设计的新一代智能爆破测振仪，能够最大程度地简化爆破测振现场工作流程，爆破现场自动设置触发电平，达到“一键完成爆破测振操作”的智能化效果，同时可靠性、稳定性大大增强，续航时间也显著增加。

1.3 试验测点布置

每次测量共布置5个测点，在楼房1、5、10、15和20层楼梯处靠近楼房的主立柱布设，对应的楼层高度分别为0 m、15 m、30 m、45 m和60 m。每个测点布置一个传感器，测点编号为1#、2#、3#、4#和5#。测点距爆心的水平距离为100 m～150 m。

爆破振动测试方案：5个测点所在的直线与炮孔平行。爆破前20 min将传感器置于地板，周围用石膏粘附，保证传感器与建筑物一起振动。粘附完成以后，爆破前5 min打开仪器。每次测试严格要求测点的垂直方向保持在一条直线上，因为炮孔位置和最大段药量每次都不同，所以测得振动速度不同。

1.4 监测结果

对不同的爆心距离和最大段药量的爆破振动进行监测，在最大段药量为 20 kg，爆心距测点的水平距离为110 m时，实测所得三维爆破峰值振速、主频率和振动持续时间（见表2），其中，5#测点峰值振速最大为0.453 cm/s，主振频率为8.85 Hz，振动持续时间为4.265 s。波形如图1所示。

表2 数据统计表

图1 5#测点的振动波形

2 爆破振动传播规律研究

2.1 爆破振动传播规律分析

爆破振动传播规律的分析一般是用线性回归分析方法来拟合分析，数据的回归分析在实际工程中具有广泛应用。大量的现场实测和试验结果表明：爆破振动强度主要与爆心距、装药量、岩土性质、地形条件等因素有密切关系，《爆破安全规程》（GB 6722-2014）中推荐的峰值振速衰减规律计算公式为萨道夫斯基公式。

式中，V为质点振动速度，cm/s；Q为最大段药量，kg；R为爆源至测点的水平距离，m；K、α为与地形和地质条件有关的参数。

使用萨道夫斯基公式探讨峰值振速随高度变化的衰减规律，首先，对公式左右两边取对数，得到式（2）：

将爆心距R、单段药量Q和峰值振速V代入以上所设的x，y表达式，可得数据组（xi,yi），其中i=1,2,3,…,40。对数据进行最小二乘法的线性拟合得出A、B，进而可算出系数K和α的值。

相关系数r反应拟合效果的好坏，其数值在0～1之间，越接近于1，效果越好。

本次试验采用origin软件对A和B进行拟合，对不同的爆心距离和最大段药量的爆破振动进行监测，采用1#测点的垂向峰值振速、径向峰值振速和切向峰值振速对A和B进行拟合。试验数据见表3。

表3 1#测点三维峰值振速

2.2 爆破振动衰减规律研究

在进行数据分析之前，先建立拟合函数y=A+Bx，拟合采用非线性曲线拟合，垂向峰值振速拟合结果如图2所示。

由图2可得，A=6.5873，B=2.339 25，所以k=eA=725.818 51，α=B=2.339 25。

图2 垂向峰值振速拟合曲线

径向峰值振速拟合结果如图3所示：

由图3可得，A=4.9672，B=1.878 42，所以k=eA=143.624 17，α=B=1.878 42。

图3 径向峰值振速拟合曲线

切向峰值振速拟合结果如图4所示。

由图4 可得，A=6.722 38，B=2.334 26，所以k=eA=830.792 45，α=B=2.334 26。

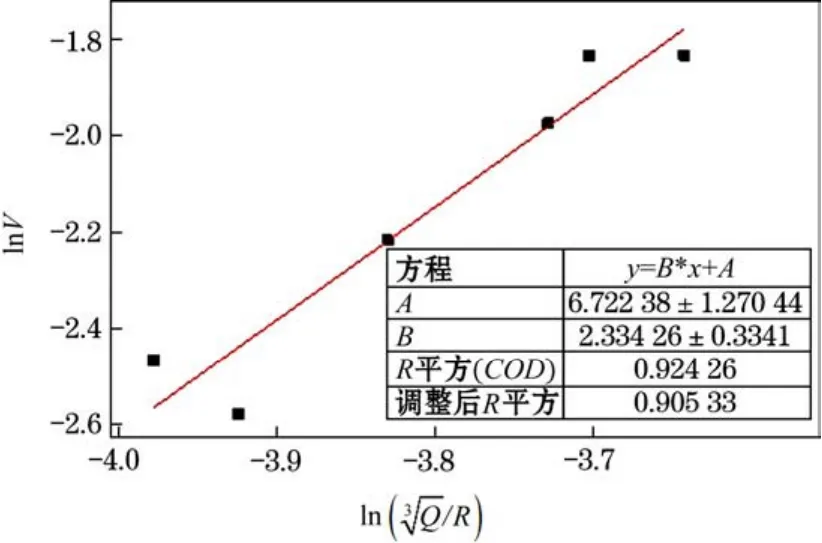
图4 切向峰值振速拟合曲线

综上所述，垂向峰值振速的衰减系数α大于切向的，切向的k值大于垂向的，径向的k和α都明显小于垂向和切向。由此可知，爆破振动波从爆源处传播到建筑物的过程中，垂向峰值振速的衰减速度大于切向的，径向峰值振速的衰减速度介于切向和垂向之间。爆破峰值振速随建筑物距爆心的水平距离和最大段药量变化的衰减规律如下。

垂向峰值振速衰减公式为：

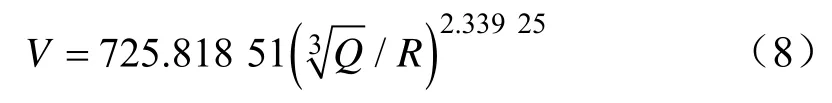
径向峰值振速衰减公式为：

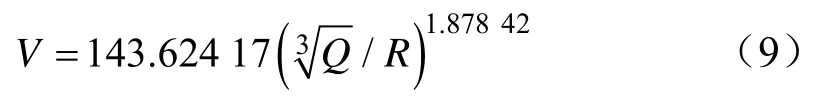
切向峰值振速衰减公式为：

2.3 测试结果与计算结果的对比分析

根据爆破试验现场所测的峰值振速，结合振速衰减公式所计算的结果进行对比分析，测试结果与计算结果见表4。

由表 4可知，计算值与实测值的最大误差为0.012 cm/s，最大误差率为 8.2%，平均误差率为4.2%。实际测量结果与计算结果相符合，因此，在爆破设计的过程中，已知爆心距建筑物的水平距离和建筑物爆破振动允许最大速度，即可求出安全允许的爆破最大段药量。

4 爆破振动对建筑物影响分析

爆破振动对建筑物产生的影响，取决于爆破振动的振动幅值、主频率和持续时间等。爆破振动的峰值、主频率和持续时间随楼房高度变化较大，表现出不同楼层高度的振动峰值、主频率和持续时间并不一致。通过对楼房不同高度的楼层进行现场爆破振动测试，分析高层楼房对爆破振动的反应规律，研究选取最大段药量为 20 kg，爆源距建筑物的水平距离为110 m的测点作为研究对象，试验数据见表5。

表4 三维振速实测与计算结果分析/(cm/s)

表5 三维爆破峰值振速随楼层高度变化统计

由图5可知，垂向峰值振速随着楼层高度的增加而增大，增速先快后慢。切向峰值振速随着楼层高度的增加呈现出先增加后减小，到达最小值时再增加。径向峰值振速随着楼层高度的增加呈现出先增加后减小、再增加后减小的变化趋势。在垂向方向上，出现了高层放大效应，到达顶层时，垂向峰值振速大于径向峰值振速和切向峰值振速。

由图6可知，随着楼层高度的增加，在切向方向上，主频率始终保持不变，径向方向上，主频率先快速减小为 1#测点的一半，然后随着高度的增加，再增加后减小，减小到8.24 Hz时不再变化。垂向方向上，主频率先快速减小，减小到 8.85 Hz时，随着楼层高度的增加，主频率保持不变。

图5 三维峰值振速随楼层高度的变化

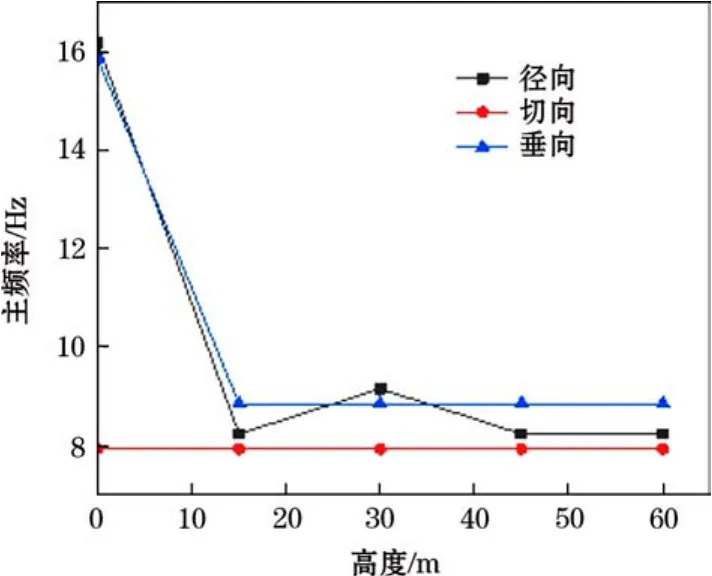
图6 三维振动主频率随楼层高度的变化

图7 振动持续时间随楼层高度的变化

由图7可知，三维振动持续时间随着楼层高度增加的变化规律为：随着楼层高度的增加，在径向方向和切向方向上，振动持续时间都是先减小后增加，增加到一定的数值后，随着高度的增加，持续时间保持不变。垂直方向上，持续时间先缓慢减小，当楼层高度为15 m～45 m时，持续时间快速下降，当楼层高度大于45 m时，随着楼层高度的增加，持续时间快速增加，在楼顶时，持续时间小于楼层底部。