锚杆锚固质量应力波检测的固结波速探索
2021-04-17郑军
郑军
(攀枝花市兴茂动力设备安装有限公司, 四川 攀枝花市 617000)
0 引言
锚杆锚固质量的判别是评估井巷围岩控制效果的一项重要内容[1]。当前,对锚固质量的判断主要有两类方法[2]:一是基于锚杆拉力仪的拉拔性检测,该方法虽可靠度较高,但属于破坏性抽检,实施过程中会降低锚杆对岩体的锚固作用[3];二是基于应力波测试的无损检测,其原理是向锚固系统注入冲击性扰动,通过检测系统的振动信号,识别有关振动参数,并以此作为反映系统锚固质量的表征,此方法具有实时、高效的优点,是一种无损伤的间接测试法[4]。相关研究提出了诸多用于表征锚固质量的参数,包括振幅比、波阻抗、信号相速率、能量速率、衰减系数等[5]。其中,固结波速是一个广泛被大家认可的参数,其物理含义是激发应力波在锚固段内的传播速度[6]。固结波速会随锚固强度的不同而发生变化[7],当锚固质量较好时,意味着固结强度较高,固结波速将趋近围岩体的波速;当锚固质量较差时,意味着锚杆杆体与锚固剂或锚固剂与围岩之间的粘结强度不足,固结波速会趋近于锚杆杆体的波速。因此,固结波速便成为能综合体现锚固优劣的指标[8]。但是,现实中通过分析应力波检测信号来获得固结波速往往会遇到难以克服的困难,原因是确定固结波速的锚杆底端反射难以被识别[9]。由于锚固段内应力波能量的散射以及固端界面应力波的多次反射,特别是锚固质量越好时行波的能量散射愈明显,导致到达底端的应力波大大减少,底端反射信号非常微弱[10]。因此,需要另辟蹊径,破除仅仅依靠识别底端反射来确定固结波速的思维困局,寻找其他能确定固结波速的易识别振动参数。为此,本文利用波动理论,建立锚固系统振动力学模型,探索固结波速与易识别振动参数的关系,为固结波速的求解提供参考。
1 锚固系统振动力学模型
激振力作用下端锚锚固系统如图1所示。f为激振力锤施加于锚杆外端的振源冲击力,kN,因其引起的锚固系统振动信号由加速度传感器采集;l1和l2分别为锚杆自由段与锚固段长度,m;d1与d2分别表示锚杆自由段和锚固段直径,mm;ρ1为锚杆杆体材料密度,ρ2为树脂锚固剂密度,kg/m3。假设从锚杆外露端起建立X坐标轴,则锚固系统任意截面位置x处的振动位移为u,u是与x和振动时间t有关的物理量。
对于锚杆自由段(x∈[0,l1]),其振动位移u1(x,t)满足波动方程:

式中,c1为应力波在自由段内的传播速度,m/s;=E1/ρ1,E1为锚杆杆体弹性模量,GPa。

图1 受激振力作用的锚固系统
利用分离变量法对式(1)求解得:

其中,ωn为振动固有频率,Hz;A、B为待定系数,由边界条件确定。
由于自由段可等效成是一端受载,一端有集中质量(锚固段)的杆件模型,则其固有频率ωn=同时为研究方便,取振动基频,即n=1时,另外,规定振动时间t为应力波单程行波时间,即t∈ [ 0,l1/c1]。
当t=0时,在x=0的边界上,根据冲量定理,有:

在x=l1的边界上,根据牛顿定理,有:

式中,m1和m2分别为自由段与锚固段质量,kg;Δt为冲击荷载作用时间,一般取1/1000~1/10 000 s;A1为锚杆杆体断面面积,m2。联合式(3)、式(4)解得待定系数:

其中q=l1/l2。
同理,对于锚杆锚固段(x∈[l1,l1+l2]),其振动位移u2(x,t)也满足波动方程,解的形式为:

式中,c2为固结波速,m/s;D、F为待定系数。
因为锚固段可等效成固端自由、底端固定的杆件,所以其振动基频ω= π ·c2/ 2l2。应力波在锚固段内单行传播时间t∈[l1/c1,l1/c1+l2/c2]。
当t=l1/c1时,在x=l1的边界上,有:

在x=l1+l2的边界上,有:

联合式(6)、式(7)解得待定系数:

下面结合算例对振动模型进行说明。算例:一端锚锚杆长2.5 m,锚固段长0.5 m,钢筋杆体密度7900 kg/m3,杆体直径20 mm,树脂锚固剂密度1500 kg/m3,锚固段直径30 mm,杆体外端施加1个3 kN的激振荷载,荷载作用时间10-3s,假设应力波在自由段和锚固段的波速分别为 5000 m/s和3300 m/s。将上述参数代入式(2)和式(5)中得到行波单程时锚固系统振动位移规律,如图2所示。
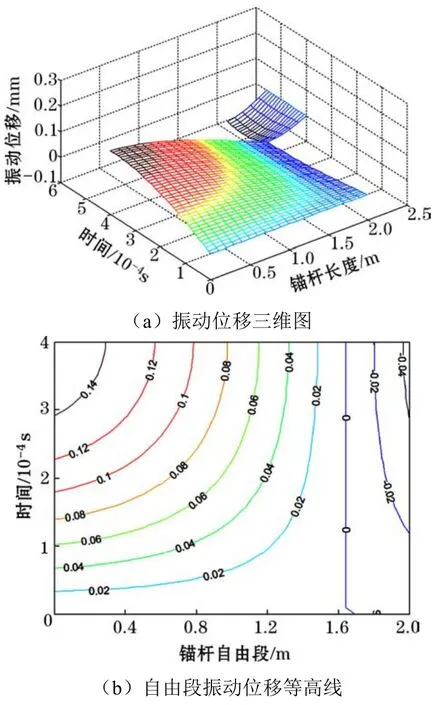

图2 锚固系统振动位移分布
由图2可知,对于自由段,从空间维度上看,振动位移沿锚杆从外向内逐渐减小;从时间维度上看,振动位移随时间延长而增大,但距振源的位置越远,位移增幅越小。说明自由段内不同截面位置介质的振动幅度不等、振动分布不均匀,体现了振动能量在时空上的不均衡传递。显然,最外端截面的振动位移最大,且时间效应也最显著,而在应力波沿杆体传播的过程中,振动的时空效应均出现减弱,这与声波检测信号呈现的振幅逐渐衰减规律一致。另外,位移在杆体1.68 m处为0,且该位置前后位移出现反向,表明受应力波扰动作用,0 m~1.68 m的杆体段与1.68 m~2.0 m的杆体段内介质分别呈受压和受拉状态,杆体内应力波为纵波,体现了纵波传播的疏(拉)密(压)特征。
对于锚固段,从空间维度上看,振动位移在固端界面最大,在底端界面为零,在两界面之间逐渐减小;从时间维度上看,振动位移随时间延长先增大后减小,呈“倒钟形”规律分布,“钟顶”所对应的时刻为固结波(锚固段内传播的应力波)传播耗时的一半。整体看,锚固段振动位移在时空上的分布较为规律、变化均匀。特别是固端振动明显、底端振动微弱,这一现象与现实声波检测信号呈现的固端反射清晰、底端反射难于识别的规律相一致,为底端反射识别困难提供了充分的理论解释。说明利用声波检测的固端反射信号易于识别的特点,通过理论模型建立固端振动位移与固结波速这两个物理参数间的关系,可准确容易地获得固结波速,避开了必须通过识别底端反射信号来获取固结波速的技术难题。
2 影响固结波速与固端振动的因素
为弄清锚固参数对固结波速与固端振动位移的影响程度,采用正交试验法对这些因素的影响力进行分析。试验因素包括锚杆自由段长度、锚固长度、锚杆直径、锚固段直径以及锚固剂密度,各因素选择5个水平,见表1。试验方案及结果见表2。试验结果选择固结端最大振动位移,其值是将各方案参数代入式(5)计算而得。式(5)所需的其余参数同上节算例。结果显示,锚固段长度这一因素的极差最大,说明其对固结波速及固端振动的影响最明显,是主控因素。
图3反映了不同锚固长度下固端最大振动位移与固结波速的变化规律。可以看出,因为锚固段介质质点的振动本质上服从正弦函数规律,锚固段长度作为正弦函数的一个参数,其变化改变着函数的相位,故当锚固段长度不同时,固结波速与固端最大振动位移的关系曲线均不相同。例如,同为2.5 m长的两根锚杆,一根锚固长度为 0.4 m,另一根锚固长度为 0.5 m,其余锚固参数相同,若测得这两根锚杆的固端最大振动位移均为-0.1 mm,则两者对应的固结波速分别为3600 m/s和4840 m/s,代表着两种不同的锚固质量。图3还显示出在表征锚固质量由好到差的固结波速所涵盖的3000 m/s~5000 m/s的区间内,固端最大振动位移落在-1.5 mm~1.5 mm的范围,而其中大部分位移值又分布在-0.02 mm~0.02 mm这个范围内,在此范围内,位移随波速增加而缓慢增大(或减小);在此范围外,位移随波速增加则加速增大(或减小)。这些位移骤变范围所对应的固结波速区间因锚固段长度的不同而各异,如:锚固段为0.3 m、0.4 m、0.5 m、0.6 m、0.7 m时,固结波速区间分别为3800 m/s~4400 m/s、3600 m/s~4000 m/s、4600 m/s~5000 m/s、3000 m/s~3400 m/s以及 3600 m/s~4200 m/s。由此说明这些波速值往往对应着振幅明显的固端振动,传感器采集到的固端反射信号会较强,易于识别。另外,上述的固结波速区间内还存在一个值,它会使振动位移发生突跃,不过突跃点两侧曲线呈单调变化,表明不会有一个振动位移对应多个固结波速的情形出现,体现了由振动位移标定固结波速的准确性。

表1 试验因素及其水平

表2 试验方案与结果
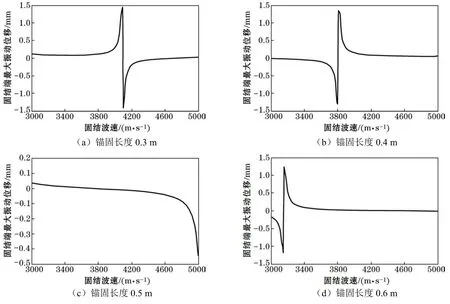

图3 固结波速与最大振动位移的关系曲线
3 结论
(1)分别对端锚锚固系统的自由段和锚固段建立力学模型,获得激振力作用下锚固系统的振动响应。在锚固段上,固端界面振动最大,底端界面无振动,振动从固端到底端逐渐减弱,并在时空上呈“倒钟形”规律分布。
(2)建立固结波速与固端最大振动位移间的函数关系,分析相关锚固参数对该函数关系的影响程度,得到锚固长度为其主控因素的结论。分析得出不同锚固长度下,固结波速与固端振动峰值的变化规律。
