K-Means 聚类中心最近邻推荐算法

郝雅娴

山西师范大学数学与计算机科学学院，山西临汾041000

0 引言

协同过滤算法技术［1］已经被成功的运用到推荐系统中，基于协同过滤推荐算法的假设是:如果用户对相同项目评分相似，那么这些用户的兴趣也是相似的.协同过滤算法通过分析不同用户对不同项目的评分，对用户的兴趣进行建模，并为用户提供推荐服务.基于协同过滤算法的推荐一般有三步:即用户数据收集，数据预处理以及做出推荐［2］.

基于最近邻的推荐算法是计算每个用户或者项目的最近邻，通过最近邻进行评分预测［3］，因为初始数据数据量与稀疏性非常大，因此会导致KNN 运算时间较长，从而导致推荐结果不理想［4，5］.目前一个较为成功的方法就是利用聚类算法减少推荐算法的计算复杂度.聚类算法可以将对象划分为若干个类别，类别中任意两个对象的相似度高于不同类别的相似度，在聚类算法的基础上，推荐算法可以向用户推荐受用户欢迎的项目，并且降低算法的计算复杂度［6，7］. Shinde 等人利用聚类算法处理推荐算法中的冷启动问题［8］，Ghazanfar 等人利用聚类算法鉴别并处理推荐算法中的gray-sheep 用户问题［9］，文献［10］中首先对项目进行聚类分析，然后将聚类后的聚类中心结果结合已评分的数据来计算用户相似性.

本文将KNN 算法与Kmeans 算法相结合，利用目标用户所属的聚类中心代替目标用户寻找其最近邻，降低了KNN 算法单独运算时的计算复杂度.本文提出的算法总体可以分为3 步:

首先对初始数据集进行聚类运算，然后找出数据集的聚类中心;

其次寻找每个用户所属的聚类中心，将聚类中心代替目标用户放入KNN 算法中寻找用户的最近邻;

最后做出评分预测.同时又考虑到目标用户与聚类中心对预测评分值的影响，于是在本文算法的基础上提出了加权的思想.如果目标用户已经在聚类中心的最近邻用户集合中就不去计算其对评分值得影响，如果不在近邻集合中，就添加目标用户与聚类中心的评分值对预测评分值的影响.算法在Movielens 数据集上进行实验，实验结果表明，推荐算法评分预测的精确度得到显著提高，而且加权之后的改进算法精确度也明显提高.

1 预备知识

1.1 K-Means 算法

K-Means 算法是无监督的聚类分析算法，其本质是通过计算不同样本间的距离来判断他们的相近关系，相近的就会放到同一个类别中.

首先随机选择一个k 值，也就是将数据分为几类.k 值就是最初选择的聚类点，又称质心;其次计算数据集中每一个样本点距离质心的距离，分别将这些样本分配到离其质心最近的那一类中;再次计算每个类中样本的平均值，将这个平均值作为新的质心，然后重复第二步;最后不断重复得到收敛质心.下面给出的是K-Means 算法的伪代码:

K-Means 算法:

1.2 基于用户的最近邻算法

基于用户的最近邻算法(K-Nearest Neighbor algorithm，KNN)是最早的协同过滤算法.其基本思想是利用目标用户近邻用户的评分值去估计目标用户对项目的评分预测值.随后基于项目u 的最近邻算法被提出.在这里只介绍基于用户的最近邻算法的基本思想，对于目标u 项目的最近邻寻找，首先定义最近邻个数k，将计算所得的相似度按从大到小的顺序排列，选取前k 个作为目标项目u 的k 个最近邻用户.寻找项目最近邻算法的关键问题是通过计算相似度来寻找最近邻，计算相似度的方法常用的有欧氏距离、余弦相似度以及皮尔逊相似度，本文采用欧氏距离方法计算相似度，计算公式如下:

式(1)中的u 与v 分别表示原始评分矩阵中的任意两个项目，ru，rv分别表示用户u 与v 对应的评分向量，sim(u，v)表示项目u 与v 之间的相似度大小.将计算所得的相似度大小保存到相似度向量矩阵中，预测评分值由评分值与相似度的加权平均值得到，即

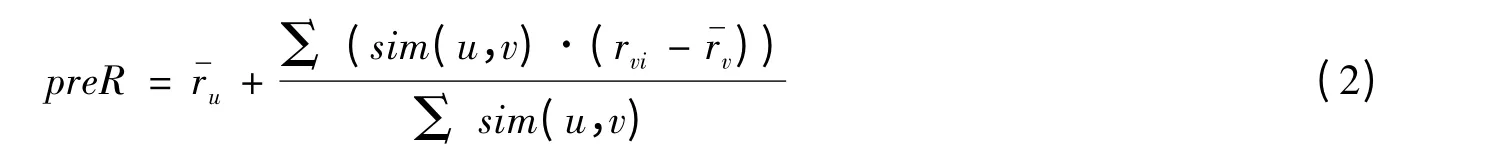
当原始评分矩阵具有极大的稀疏性时，利用相似度计算目标项目的最近邻会出现误差.因此许多学者在KNN 算法执行之前会首先对原始评分矩阵进行预处理，从而使算法的准确性提高.下面给出基于用户最近邻算法的伪代码:

KNN 算法

2 算法实现

2.1 算法步骤

第1 步～第4 步是寻找聚类中心的过程，首先针对数据集进行聚类，初始化聚类中心，计算每个样本到聚类中心的距离，第三步重新计算聚类中心，直到收敛，第4 步输出整个样本的聚类中心.

第5 行～第8 行是进行最近邻计算的过程，如果计算样本x 对商品p 的评分，首先找到样本x 所属的聚类中心.第6 行用聚类中心代替样本x 去计算最近邻，得到聚类中心的最近邻之后，通过预测评分公式计算评分值，最后输出评分值.下面给出本文算法的伪代码:

2.2 算法实例分析

下面给出实例模拟本算法的实验，首先对表1 中的数据进行聚类分析.

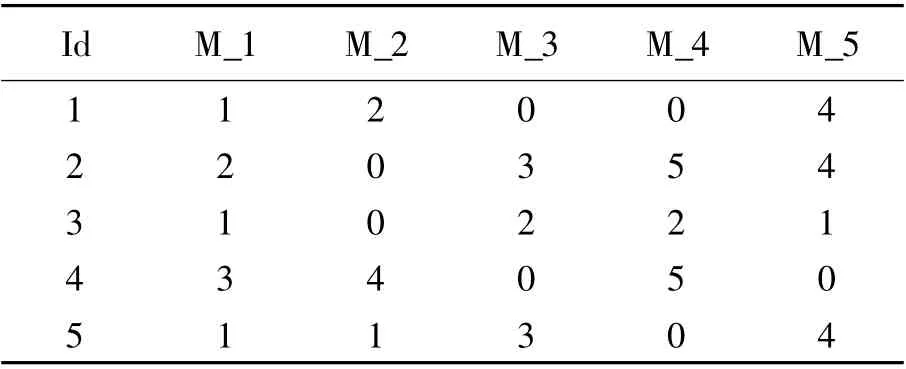
表1 原始评分表Tab.1 Original Rating

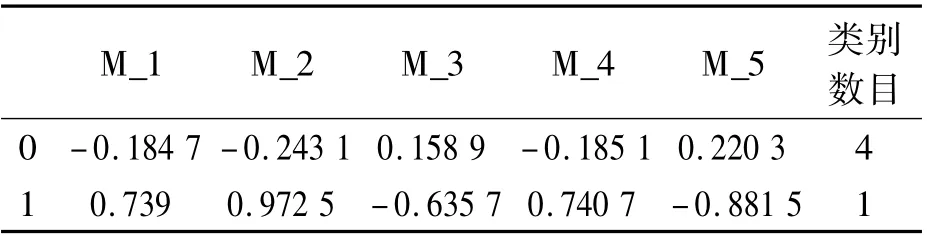
表2 聚类中心Tab.2 Cluster centroids

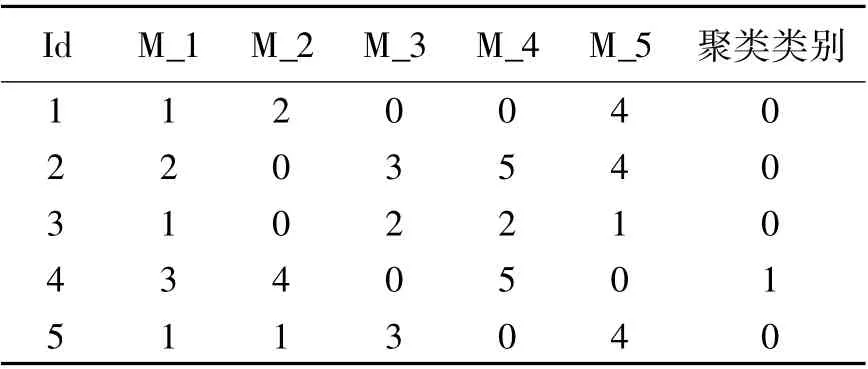
表3 聚类类别Tab.3 Clustering Categories

随机选取2 个聚类中心:Id =1，2，选择用户1与用户2 作为聚类中心;

计算样本与聚类中心间的距离，这里采用欧式距离，经过计算S(1，3)= 4.58，S(1，4)= 7，S(1，

5)= 3.16，S(2，3)= 4.47，S(2，4)= 6.48，S(2，5)

= 5.19;因为S(1，3)＞S(2，3)，所以用户3 选择用户2 作为聚类中心;

依据此规则，第一次的选择结果，组1 成员:1与5，组2 成员:2，3，4.

第二次选择聚类中心取样本平均值，不断重复以上步骤，分别得到聚类中心与样本所属的聚类类别表(表2).

根据表3 数据可知，只有用户4 属于第2 类，其余用户属于第一类，那么，接下来进行最近邻计算，如果求用户1 对M_3 的评分，则将用户1 所属聚类类别0 的聚类中心代替用户1 寻找最近邻，同样进行相似度计算.

比较相似度并找出前2 个近邻，最后根据评分预测公式进行评分估计，可得用户1 对M_3 的评分值为1.364 4，不断重复这个过程，最后可以的到完整的用户评分预测值.

3 实验结果分析

3.1 Movielens 数据集与评价指标

针对推荐算法，只有通过评测才可以了解其推荐质量.推荐系统的评测指标问题同样也是近几年来诸多学者研究的课题重点.

本算法利用均方根误差(RMSE)验证实验结果的准确性，以RMSE 值作为实验准确性的评价指标，RMSE 的值越小算法实验结果越优.计算公式如下:其中TestSet 表示测试集

MovieLens 数据集包括三个数据集.其一是一个小型的数据集，该数据集是943 个用户对1 682 部电影的评分数据信息:其二是一个中型数据集，该数据集是6 040 个用户对3 952 部电影的评分数据信息;最后是一个大型数据集，该数据集是71 567 个用户对10 681 部电影的大约有一千万条评分的数据信息.

本文实验所采用的数据集为MovieLens 数据集中的小型数据集.图1 展示了部分初始数据集，从图中可知，MovieLens 数据集是非常稀疏的.

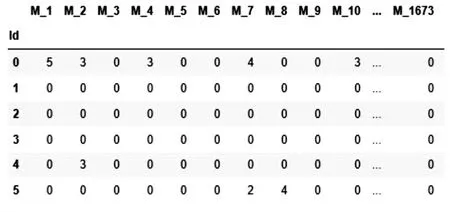
图1 MovieLens Fig.1 MovieLens

3.2 实验结果

根据算法步骤，首先对数据进行聚类分析通过对数据集进行聚类算法实验，得到以下结果:图2 列出的是经过聚类为3 的聚类运算后，每个样本所属的聚类类别情况，图2 中为部分原始数据集所对应的聚类类别，最后一列表示的是每一行样本所属类别，类别类型用0，1，2 代替.图3 为经过聚类运算之后的聚类中心.

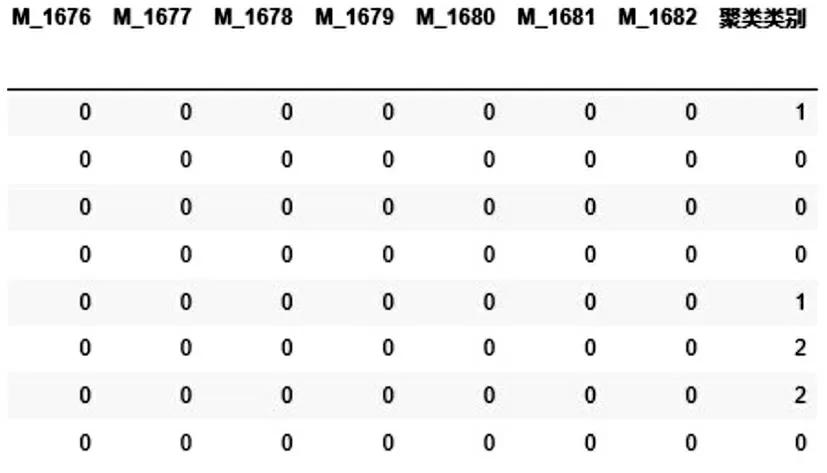
图2 聚类类别Fig.2 Clustering categories

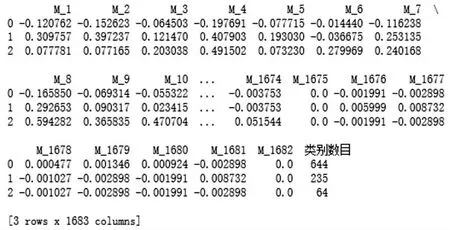
图3 聚类中心Fig.3 Cluster centroids

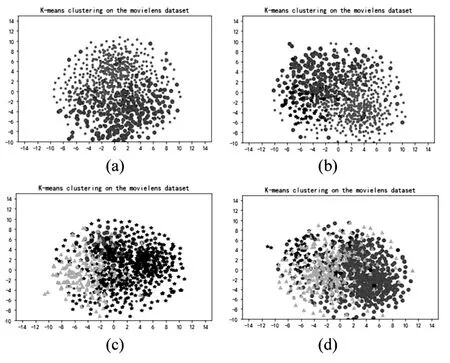
图4 聚类结果Fig.4 Clustering Results

确定聚类中心后，本文分别计算了KNN，K-Means 聚类中心算法与K-Means_w 算法下的RMSE 值，图中蓝色曲线是基于KNN 计算得到的RMSE 值，由图中可知，随着KNN 中k 值得变大，RMSE 值不断增大，这是因为原数据集有很强的稀疏性，KNN 的计算速度虽然很快，但是在样本数量很大的情况下，计算速度相对变慢，KNN 对于大多数特征下取值都为0 的数据集(稀疏数据集)来说，KNN 算法的效果并不好，所以随着KNN 中k 值得增大，RMSE 值反而增大.

图中黄色曲线是利用K-Means 聚类中心算法计算得到的RMSE 值，由图可知，确定聚类中心为2 的情况下，随着最近邻个数的增加，RMSE 值减少，随着k 值得增大，曲线将逐渐达到收敛，因为K-Means 选取的聚类中心解决了KNN 所面对的数据稀疏性问题，聚类中心是经过不断迭代之后所产生的，利用中心代替目标用户取计算最近邻，有效地解决了数据稀疏性所造成的问题.

图中红色曲线是加权后的K-Means 聚类中心算法RMSE 值，从图中可以明确地看到加权之后的算法有效地提高了算法的效率，降低了RMSE 值，加权之后的K-Means 算法考虑到的是目标用户如果是聚类中心的最近邻，就不需要重复计算目标用户对评分值得影响，如果目标用户不在聚类中心的最近邻用户集合中，应该添加目标用户与聚类中心的评分值对预测评分值得影响.

通过图中的对比，可知改进后的算法RMSE 值是最好的.表4 中给出了三个算法下不同K 值所对应的RMSE 值，用这个数据可以模拟上图，从表中也可以直观的对比得出，RMSE 在K-Means_w 算法下的结果是非常可观的.

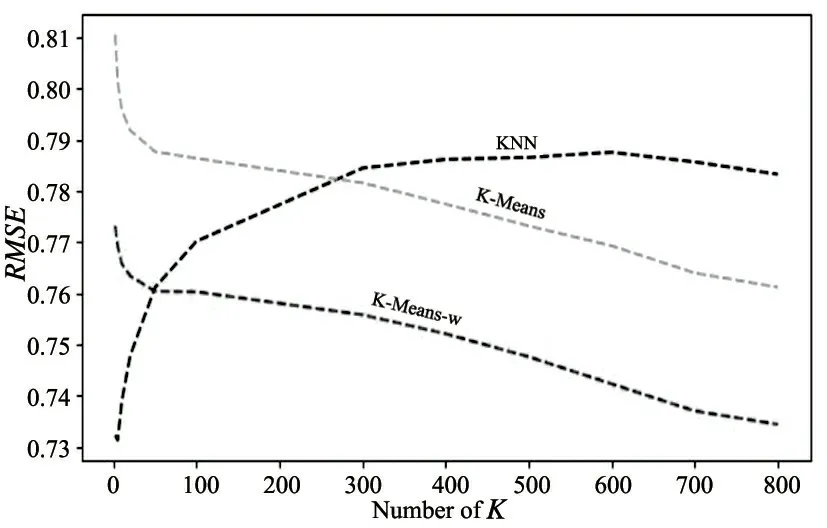
图5 RMSE 值对比图Fig.5 RMSE comparison

表4 算法实验结果(RMSE)Tab.4 Experimental Results(RMSE)

4 结论

本文提出的K-Means 聚类中心最近邻推荐算法，通过将KNN 算法与K-Means 算法相结合，在对未知评分项预测时，同时考虑被预测的目标用户与其聚类中心对评分预测值的影响，降低了稀疏性问题对KNN 算法的影响，同时提高了算法精确度，使得推荐结果合理性更高.实验结果证明，本文提出的算法对比KNN 算法得到更准确的推荐结果.在以后的工作中，会继续针对稀疏性问题进行深入研究.