基于混合精度量化的空时编码大规模MIMO系统性能

陈 林，王传旭，王 康，李 学，张红伟

（安徽大学电子信息工程学院，合肥230601）

引 言

随着智能设备及各种终端设备的数量急剧增长，人们对移动数据量的需求也在逐年增加，5G无线通信系统成为近年来的研究热点。大规模多输入多输出（Multiple input multiple output，MIMO）作为一种十分有潜力的技术，可以很大程度地提高系统的能量效率和可达数据速率［1］。然而当采用大规模的天线阵列时，每一根天线都需要一条专用的射频链路，其所产生的成本和功耗是十分巨大的。解决方法之一就是在射频链路中采用低分辨率的ADC以降低系统部署成本与功率消耗［2］，因为低分辨率的模数转换器（Analog to digital converter，ADC）工作时消耗的功率较低且硬件成本也比高分辨率ADC更低。

由于在系统中采用纯低精度量化的结构会造成系统性能的损失，所以学术界提出混合精度量化的结构，文献［3］率先讨论了一种采用混合ADC结构的大规模MIMO系统，即保留一小部分高分辨率ADC，其他射频链路均配置1 bitADCs。这种混合精度量化的结构在实际的大规模MIMO系统部署中极具潜力，因为采用这种混合结构仍然可以得到很大部分的系统性能增益。在这种结构中，保留的一部分高分辨率ADC被用来以轮询方式进行信道估计，获得更加完美的信道状态信息。文献［4］采用AQNM模型对量化进行建模分析，研究低分辨率ADC的引入对系统性能带来的影响，分析认为可以通过增加量化比特位数与接收天线数的方式，提升系统的和速率。文献［5］对系统频谱效率与能量效率两个指标进行推导与研究，分析了混合精度量化对系统性能产生的影响。文献［6］推导出MRC检测器下的混合精度量化大规模MIMO系统的可达数据速率的闭式表达式近似公式。文献［7］给出了大量关于低精度量化技术对系统性能影响的数学结论，被广泛关注，并用于推导系统频谱效率的近似表达式。这些文献都验证了在大规模MIMO系统的接收端采用混合精度量化技术的可行性。但是现阶段大量的研究集中在发射端为多个单天线用户，且为了得到更优的系统性能都在接收端采用了MRC接收。而对于发射端采用多根天线情形下混合精度量化的性能研究有待进一步讨论。

本文从系统可达数据速率和能量效率两个方面，对基于混合ADC结构的空时编码大规模MIMO系统的性能进行推导与研究。与之前大多数工作不同，本文考虑在发射端为用户配置多根天线的场景。在发射端多天线的系统中，MRC接收就不再适用了，本文对两根发射天线的情况进行研究，选择空时编码中极具代表性、译码简单的Alamouti编码［8］方式发送信号以期得到与单发多收系统采用MRC接收近似的系统性能，同时在基站端采用混合精度量化结构以降低大规模MIMO系统的硬件成本和电路功耗。推导和仿真结果证明在发射端多天线的大规模MIMO系统中，混合ADC架构实际上是有用的，可以提供与理想量化ADC结构近似的性能，同时可以降低信号处理的复杂性和功耗。同时，在发射端采用空时编码的方式，系统的发射分集增益增加了一倍。

1 系统模型

本文考虑一个上行大规模MIMO系统，假设发送端有两根天线，并且采用Alamouti编码方式发送信号，基站端有M根天线分别对信号进行接收合并处理。接收端为了降低系统的成本与功耗，采用混合精度量化的结构，在其中M0根天线所连接的射频电路中使用高分辨率ADC，而在M1=M-M0根天线连接的射频电路中使用低分辨率ADC。具体模型如图1所示。

这里，假设系统接收端与发射端之间的信道衰落系数服从莱斯分布，按照文献［9］，本文将莱斯衰落信道写作

式中：G表示收发端间的信道矩阵；D表示系统中的大尺度衰落，D的各项元素用βn表示，即Dnn=βn，n=1，2；H表示系统中的小尺度衰落。根据文献［10］，将莱斯信道模型中小尺度衰落部分表示为确定分量与随机分量Hω的和，其中确定部分的值与视距传播路径相关，而随机部分的值则与散射信号相关，满足瑞利分布，于是可以将H写作

图1 两发多收的大规模MIMO系统模型图Fig.1 Mixed-ADCs massive MIMO system model

式中，小尺度衰落的确定部分H元素可以写作

式中：θn表示第n根发射天线发射符号的到达角，k=2πd/λ，λ表示信号波长，d表示天线间的距离。除此之外，对角阵Ω的元素为莱斯K因子Kn。

用pu表示用户端的发射功率，s表示发射向量。那么大规模MIMO系统接收端接收到的信号就可以写作

式中n表示信道噪声矩阵。因为接收端采用混合ADC结构，那么这里将信道分为上下两部分进行分析

式中：G0表示发射天线与M0根配置高分辨率ADC的天线之间的信道矩阵，G1表示发射天线与M1根配置低分辨率ADC的天线之间的信道矩阵。那么系统接收到的信号也可写作

式中：Y0表示接收端M0根配置高分辨率ADC的天线接收到的信号矩阵，Y1表示接收端M1根配置低分辨率ADC的天线接收到的信号矩阵。

1.1 信号发射

为了发射端能够充分挖掘空间资源，得到全分集增益，发射端采用Alamouti编码方式发射信号，通过两根发射天线在两个时间片发送不同信息及其副本。对于基站端第i根接收天线前后两个时隙收到的信号可以表示为

式中gin（i=1，2，…，M）表示发端第n根天线与收端第i根天线间的信道衰落系数。

整理式（7），第i根天线上的接收信号可以表示为

那么，将M根接收天线收到的信号合并为一个矩阵表示，对于接收到的信号就可以表示为

1.2 接收端量化

对于基站接收端，M0根配置高量化精度ADC的接收天线接收到的信号为Y0，Y0通过较高比特位数的理想量化，因此对于Y0部分的第i根接收天线接收的信号可以表示为

而M1根配置低量化精度ADC的接收天线接收到的信号为Y1，Y1通过低位宽量化，利用加性量化噪声模型（Additive quantization noise model，AQNM），对于接收信号Y1量化后的输出信号可以表示为

式中，α为ADC量化增益，则失真因子ρ=1-α，当量化精度为1～5 bit时可以通过表1可以得到参考值，当量化精度大于5 bit时，失真因子可以通过计算得到近似值：。

表1 不同量化比特位数对应失真因子［11］Table 1 Distortion factor for different quantization bits［11］

根据文献［12］可知，量化噪声nq的协方差矩阵为

1.3 信号合并处理

按照Alamouti编码准则，将接收到的信号与Gi的共轭转置相乘处理，则对于M0根高分辨率ADC连接天线接收到的信号表示为

对于M1根低分辨率ADC连接天线接收到的信号量化后的信号可以表示为

生产其中Pi为生产的第i个行业的产品；消费其中Ci为消费的第i个行业的产品；出口其中Xi为第i个行业的出口；进口其中Mi为第i个行业的进口。

对于s1和s2分别有

式中：gn0表示G0的第n列，gn1表示G1的第n列。

2 性能分析

2.1 可达数据速率

这一节将对采用混合ADC结构的空时编码大规模MIMO系统的可达数据速率进行推导和分析，得到可达数据速率的近似表达式。

对于给定的信道G，根据文献［13］，有第n个信号的可达数据速率为

式中

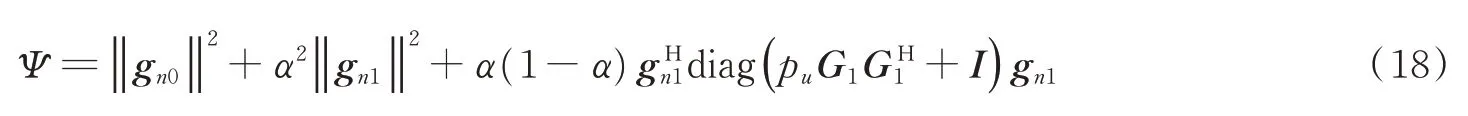
因为式中的信道衰减因子都是随机量，无法直接地得到上式所表示的可达数据速率的闭式解，所以这里借助随机矩阵理论和大数定律，结合大规模MIMO系统多天线的性质，得到它的近似表达式。

文献［7］给出引理1用于求期望的近似

根据式（19），可以将Rn近似表示为

式中

求解式（20），要先求出多项值的期望。由第一节确定的混合精度量化结构的大规模MIMO系统模型可知，。参考文献［7］中引理3，根据信道系数的相关性质，可以得到

最后，对于量化噪声引入的干扰项进行分析，易得

将式（22～24）代入式（20）后得到可达数据速率的近似表达形式

式中

从式（25）可以看出，ADC量化比特位数b，发射功率pu、高分辨率ADC和低分辨率ADC配置情况等参数都对系统的上行数据可达速率产生影响。不同于文献［14］，本文研究基于空时编码的大规模MIMO系统中采用混合精度量化的架构对系统性能的影响，并得到系统和速率的近似式。

更进一步，当莱斯K因子Kn=0时，信道会演变为瑞利衰落信道的特殊情况。此时，系统可达数据速率近似于

假设发射端发送功率pu值和基站端接收天线数M固定时，当ADC的量化精度很大时，式（25）退化为

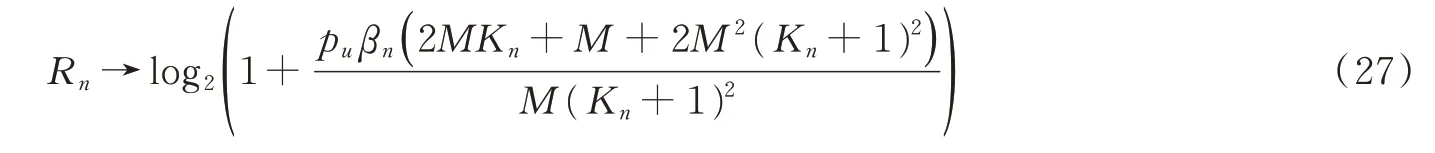
此时，b→∞，量化精度趋于无穷大，相当于理想量化，这意味着此时ADC对系统性能造成的影响基本可以完全忽略不计。对比式（25）和式（26），可以发现与量化精度b有关的量化因子α同时存在于有用信号与干扰信号中，对两部分都造成了影响，进而影响系统性能，但是由于采用混合精度量化的结构，所以量化只影响到由M1根配置低量化精度ADC的天线接收的部分。

2.2 能量效率

2.1节对空时编码的大规模MIMO系统接收端采用混合ADC结构时的系统可达数据速率进行了分析。研究表明，纯高精度量化的大规模MIMO系统的和速率是优于混合精度量化场景下的系统的，但是这种高性能是以更高的硬件成本和功率消耗为代价换取的。因此，在实际的大规模MIMO系统部署中应当考虑能量效率和功率效率的合理折中。图2所示为基站端采用混合精度量化架构下的功率消耗模型。

图2 基于混合ADC结构的大规模MIMO系统接收机模型[5]Fig.2 Receiver in massive MIMO system with mixed-ADCs[5]

一般地，一个通信系统的能量效率［15］通常表示为

式中：系统传输带宽W设为1 GHz，频谱效率R由2.1节推导得到，Ptotal表示系统总功耗。根据图2，系统总功耗可以表示为

式中：PLO表示本地振荡器消耗功率，PLNA表示低噪放大器消耗功率，PM表示混频器消耗功率，PAGC表示自动增益控制部分消耗的功率，表示低分辨率ADC消耗的功率，表示高分辨率ADC消耗的功率，PBB表示基带单元所消耗的功率，c表示一个标志位，具体的数值与ADC的量化比特位数有关：

根据文献［16］可知，ADC所消耗的功率值是由其量化精度与抽样速率共同决定的，则有

式中：fs表示抽样速率，b表示ADC的量化精度，FOMW是估计ADC功耗时常用的瓦尔登ADC性能因子［16］，是瓦尔登通过速率和ADC量化精度评估ADC功率效率的因子。根据目前技术，FOMW在1 GHz带宽时的能量消耗值大约为FOMW=5～15 fJ/conversion-step，表示ADC每一次转换的步骤大约要消耗5～15 fJ的能量［17］。

3 仿真结果

本节给出仿真结果，证明2.1节中，式（25）推导出近似表达式的准确性，同时更进一步地研究混合ADC结构对空时编码大规模MIMO系统性能的影响。假定系统发射端有2根天线，基站端M根接收天线，其中M0根配置高分辨率ADC进行理想量化，M1根配置量化比特位数为b的低分辨率ADC，而且在发射端采用Alamouti编码方式发射信号。系统仿真参数如表2所示。

表2 系统仿真参数Table 2 Simulation parameters

根据表2的参数配置大规模MIMO系统，得到系统量化比特位数与频谱效率关系图如图3所示。从图3中可以得到基于蒙特卡洛方法仿真得到的频谱效率与本文中推导的频谱效率近似表达式（25）之间的关系，仿真值与推导值在特定点处重合验证了近似表达式的准确性。从图3中3条折线的差距也可以看出当低分辨率ADC的量化精度较低时（1～3 bits），随着混合ADC架构中高分辨率的ADC比重逐渐增加，系统的频谱效率也会逐渐升高。而对于任一种混合ADC配置模式，随着接收端低分辨率ADC量化精度的增加，系统频谱效率也逐渐增大，最后收敛到一个上限，上限为理想量化情况下的系统频谱效率。

进一步，对系统能量效率进行分析，根据文献［18］，系统功率的主要仿真参数如表3所示。

图3 不同量化比特位数的系统上行频谱效率,M=200Fig.3 Spectral efficiency of massive MIMO system with STBC against different quantization bits where M=200

根据表3给出的系统参数，对不同量化比特位数下的系统能量效率进行仿真分析。仿真结果如图4所示，分别对4种情况进行仿真：（1）150条链路中配置低分辨率ADC，另外50条配置高分辨率ADC；（2）190条链路中配置低分辨率ADC，另外10条配置高分辨率ADC；（3）200条全部配置低分辨率ADC；（4）200条全部配置高分辨率ADC，作为理想量化的对照组。由图4所示的仿真结果可以看出采用混合量化结构的系统能量效率要优于理想量化的情况，且采用纯低精度量化结构时系统的能量效率最高。更进一步地，对比图4中两种配置不同的混合量化结构可以看出系统能量效率随着混合精度量化结构中高分辨率ADC的比例增加而降低。虽然低精度量化可以带来更好的能效性能，但是频谱效率比混合精度量化要低得多。此外，混合精度量化结构由于保留了部分高分辨率的ADC，所以在信道估计方面比低精度量化的性能更好，可以得到更完美的信道状态信息。综合以上，采用混合精度量化虽然牺牲了部分的能量效率，但是在性能方面可以得到比低精度量化更好的效果。

表3 系统功率仿真参数［18］Table 3 Simulation parameters of system power［18］

进一步地对系统频谱效率和系统功率消耗的关系进行仿真，仿真结果如图5所示，分别对3种ADC配置方案进行仿真：（1）100条链路中配置低分辨率ADC，另外100条配置高分辨率ADC；（2）140条链路中配置低分辨率ADC，另外60条配置高分辨率ADC；（3）200条全部配置低分辨率ADC，作为纯低精度量化的对照组。在每一种配置下，分别对不同量化比特位数进行仿真，ADC量化精度从左到右逐位增加。随着ADC量化精度的增加，系统的频谱效率增加并最终趋于一个上限值，同时ADC功率消耗也随着量化精度增加而指数增加。从图5中可以看出，混合精度量化的结构消耗的功率比低精度量化要高，但是在较低量化位数的情况下，系统频谱效率的提升较大。当量化比特位数从1 bit增加到4 bit时，系统频谱效率显著增加，而接收机的功率消耗增加量很小，几乎可以忽略。而继续增大量化比特位数，系统的功耗会显著增加。这表明，当系统中低分辨率ADC采用较低精度（约为3 bit或4 bit）时，混合精度量化的结构可以得到频谱效率和功率损耗的一个更好的折中。

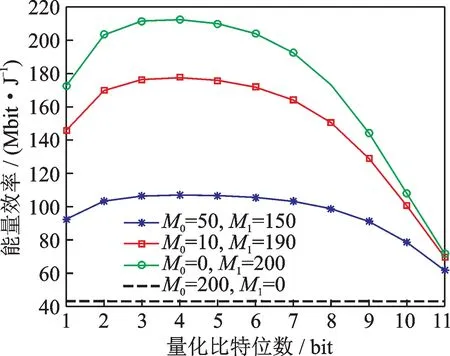
图4 不同量化比特位数下的系统能量效率Fig.4 Energy efficiency of massive MIMO system with STBC against different quantization bits

图5 系统频谱效率与接收机功耗,K=10 dB,b=1 bitFig.5 Trade-off between power consumption and spectral efficiency of massive MIMO system with STBC where K=10 dB,b=1 bit

4 结束语

针对发射端多天线的大规模MIMO系统可能出现的系统成本过高和功率损耗大的问题，本文提出了采用空时编码与混合精度量化结合的方法。当发射端配置两根天线时，传统的MRC接收不再适用，因此本文采用Alamouti编码，获得更多的分集增益并提升传输可靠性。推导和仿真结果表明，采用混合ADC的结构可以很大程度地改善系统的能量效率，同时得到近乎理想的系统可达数据速率。保留一部分的高分辨率ADC也使得接收端的信道估计变得更加容易。而且，空时编码也使系统的发射分集增益提升了一倍。因此，在多发射天线的大规模MIMO系统中采用Alamouti编码结合混合ADC结构的方法降低系统成本与功耗是可行的，为发射端多天线的大规模MIMO系统实际部署提供了理论基础。