高速干切滚齿工艺参数的多目标优化与决策方法
2021-04-15倪恒欣阎春平陈建霖侯跃辉
倪恒欣 阎春平 陈建霖 侯跃辉 陈 亮
重庆大学机械传动国家重点实验室,重庆,400044
0 引言
高速干切滚齿工艺作为一种绿色高效的齿轮成形工艺,在加工过程中不使用切削液且切削速度高,近年来得到了大量的关注和研究[1]。高速干切滚齿工艺对加工条件要求较高,不合理的加工工艺参数会严重影响齿轮的形状误差、齿向误差以及加工能耗。
工艺参数优化与决策能有效优化加工工艺参数,而无须改变加工硬件环境。国内外学者在常见的机械加工方式如车削、磨削、铣削、钻削等工艺优化上已取得不错的研究成果,但大部分研究集中于经济型指标如加工成本、加工时间、加工质量等的优化,只有部分学者注意到环境因素的重要地位,将能耗、碳耗作为优化目标。
对于滚齿工艺参数优化,相关文献较多着眼于刀具寿命、切削热能、加工成本、加工时间、加工能耗、加工精度等目标。KLOCKE等[2]对滚齿的粗加工和精加工进行研究,将刀具寿命作为研究目标,通过不同的工艺设计来实现在两种切削过程中使用相同刀具。干式滚齿工艺不使用切削液,切削空间内的热能积累导致较大的机床热变形,针对此,YANG等[3]建立了以切削空间平均温度最低为目标的热能平衡优化模型,并采用粒子群算法对优化模型进行了验证求解。考虑到干式滚削工艺中的滚刀寿命、机床热变形误差和齿轮工件质量对切削参数比较敏感,ZHANG等[4]提出了一种干式滚齿参数优化模型,并采用迭代测试方法来获取最优工艺参数。SARI等[5]对干式滚齿精加工中滚刀的磨损问题进行了研究,基于磨损研究和理论分析构建出面向实际应用的刀具寿命方程,为滚刀参数优化决策提供了新的途径。SUN等[6]对齿轮的加工精度展开研究,将最小齿形几何误差作为优化目标,采用改进的粒子群算法对滚齿加工参数进行了优化。陈鹏等[7]以自动化加工效率和齿轮单件成本为优化目标,对齿轮高速干式滚切工艺参数优化展开了系统研究,构建了工艺参数自适应优化修正模型。李聪波等[8]以最小能耗和最短加工时间为目标,通过实验设计和帝国主义竞争算法对数控滚齿加工参数进行了优化求解。CAO等[9]将滚齿过程看作一个“黑箱”,提出一种基于支持向量机和蚁狮优化算法的参数优化决策,并利用加工实例对滚齿工艺参数进行了低碳优化。
上述研究主要通过建立工艺参数与待优化目标之间的映射关系,利用人工智能算法进行优化求解时,还需要将滚刀参数作为优化变量,建立以加工能耗和齿轮加工质量为优化目标的多目标参数优化方法,对多目标优化的求解获得的非支配解集进行重新排序和决策。
鉴于此,本文针对具体的高速干切滚齿工艺优化问题展开研究,提出一种基于改进多目标灰狼优化(multi-objective grey wolf optimization,MOGWO)算法和逼近理想解排序法(technique for order preference by similarity to an ideal solution,TOPSIS)的高速干切滚齿工艺参数多目标优化与决策方法。分析了滚齿工艺参数,将切削参数(轴向进给速度、主轴转速)和滚刀参数(滚刀直径、滚刀头数)作为优化变量,构建了以最小加工能耗和最优加工质量为目标的多目标优化模型。采用改进MOGWO算法对所建模型进行迭代寻优,利用TOPSIS对优化得到的工艺参数解集进行多属性决策,获取性能排序后的工艺参数解,并通过对比结果验证本文方法和结果的有效性。
1 滚齿工艺问题描述
工艺参数是完成工艺过程的一系列技术数据。在滚齿加工中,机床性能参数、滚刀参数、齿轮工件参数、切削参数等共同组成了滚齿加工工艺参数,不同的工艺参数对齿轮加工质量、加工能耗、加工时间、加工成本、加工效率等目标有着显著的影响。实际加工中,机床和齿轮工件是由加工任务确定的,而切削参数和滚刀参数可进行相应的调整和优化。切削参数和滚刀参数的不同取值直接影响加工能耗和齿轮加工质量,而加工能耗、齿轮加工质量作为评价滚齿加工的环境指标和经济指标,已获得了企业的广泛关注。因此,本文针对上述滚齿工艺参数展开多目标优化与决策研究。
本文将滚齿工艺问题描述表示为X={X1,X2,…},其中,Xi={wi,ci,hi}为第i(i=1,2,…)个滚齿工艺参数集,wi、ci、hi分别为第i个滚齿工艺参数集中的齿轮工件参数、切削参数和滚刀参数,且wi、ci、hi分别包含多个工艺参数属性。针对某个齿轮工件加工,可以将滚齿工艺参数变量问题描述属性表示为w=(mn,z2,αn,β0,d2,B),其中,mn为齿轮模数;z2为齿轮齿数;αn为齿轮压力角;β0为齿轮螺旋角;d2为齿轮外径;B为齿宽。与滚齿工艺参数变量问题对应的待决策工艺参数变量描述属性表示为c=(va,n0,ap),h=(d0,z0,k),其中,va为轴向进给速度;n0为主轴转速;ap为切削深度;d0为滚刀直径;z0为滚刀头数;k为滚刀槽数。待决策的工艺参数决定了滚齿工艺中的加工能耗和最终的齿轮加工质量,因此,如何优化和决策滚齿工艺参数成为了亟需解决的问题。
2 高速干切滚齿工艺参数多目标优化模型
2.1 优化变量
目前的高速干切滚齿加工大多为小模数批量加工,且滚刀的切削深度对机床变形和主轴转速的影响较小,远远不足以影响切削效果,故将切削深度ap划分到工艺参数问题描述属性里,将对切削效果影响更大的va、n0作为待优化切削参数;滚刀参数d0、z0对加工过程影响较大,因此将k设为定值,将d0、z0作为待优化滚刀参数。
2.2 多目标模型
2.2.1加工能耗模型
常见的机械系统能耗表示方法有功率表示法和单位能耗法[10]。对于滚齿加工来说,其总加工能耗可以表示为不同时段的能耗总和。一般来说,滚齿加工的待机时段、空切时段和切削时段是耗能最多的3个阶段,需要对这3个阶段的能耗进行系统分析,以构建滚齿加工能耗模型。
滚齿机的启动过程是一个相对快速的过程,其能耗通常可以忽略不计。待机时段是指机床开启后的平稳运行阶段,机床的动力辅助系统已开始运行,但是与切削有关的动力部件尚未运转,此时的功率消耗基本是一个定值,很容易从功率分析仪中获取。待机时段的能耗
Es=Psts
式中,Ps、ts分别为滚齿待机时段的功率和时间。
滚齿空切时段是指机床的滚刀主轴、工作台主轴等动力部件在无载荷工况下的运行阶段,此时的齿轮工件尚未被滚切。空切时段的能耗

式中,Pa、ta分别为空切时段的功率和时间;Psc为主轴系统运转时的辅助系统(如冷却润滑系统和风扇系统)的功率;Pn为机器空载运行时的功率;κ1、κ2为机器空载运行功率系数;La、Lr分别为滚齿轴向空切长度和滚齿径向空切长度;vr为径向进给速度;js为走刀次数,js=1,2,…。
切削时段能耗
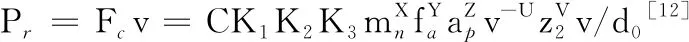
式中,Pc、tc分别为切削时段的功率和时间;Pr为废料移除时的功率;Fc为滚齿力;v为切削速度;C、X、Y、Z、U、V为切削力参数指数;K1为工件材料修正系数;K2为工件硬度修正系数;K3为工件螺旋角修正系数;Pap为切削过程的额外损失功率;ε1、ε2为额外损失功率计算系数;Ein、Uout分别为滚齿切入长度和滚齿切出长度;fa为轴向进给量。
齿轮工件的总加工能耗E=Es+Ea+Ec。
2.2.2齿轮加工质量模型
滚齿加工质量受齿形误差、齿向误差、齿廓包络误差、公法线变化误差、综合切向误差、综合径向误差、节距累积误差等因素的影响[2]。滚刀在轴向切削时,以进给量fa为单位进行等距跳动,产生齿向误差;滚切齿坯时,实际得到的齿形是多边形,因此存在齿形误差[13]。本文同时考虑齿向误差和齿形误差,以两者组成的综合误差来评价齿轮加工质量,综合误差越小,齿轮加工质量越好。
齿向误差δx和齿形误差δy分别为
为更全面地描述齿轮加工质量,引入权重系数w1、w2(w1+w2=1)来考虑δx和δy对滚齿加工质量的贡献程度,齿轮加工质量Q表示为
Q=w1δx+w2δy
2.3 优化模型和约束条件
基于上述分析,建立了以降低滚齿加工能耗、提高滚齿加工质量为目标的多目标优化模型:
minf(va,n0,d0,z0)=(minE,minQ)
(1)
s.t.va,min≤va≤va,max
(2)
nmin≤n0≤nmax
(3)
Fc≤Fc,max
(4)
(5)
式中,va,min、va,max分别为轴向进给速度的最小值和最大值;nmin、nmax分别为主轴转速的最小值和最大值;Fc,max为最大滚齿力;r为滚刀刀尖半径;Ra为表面粗糙度值。
式(2)、式(3)分别限制了轴向进给速度和主轴转速;式(4)表示切削力应不大于最大切削力,以保证加工过程能够正常进行;式(5)表明滚齿加工必须满足基本的齿轮表面粗糙度要求。
3 基于改进MOGWO算法和TOPSIS的多目标优化与决策方法
3.1 基于改进MOGWO算法的解集寻优
MOGWO算法[14]具有收敛性强、参数少、易实现等特点,在车间调度、参数优化、图像分类等领域广泛应用。本文所取的待优化工艺参数变量既包含连续的变量va、n0、d0,又包含离散的变量z0。利用MOGWO算法优越的寻优性能,在满足各种变量约束的条件下,对高速干切滚齿工艺参数优化问题进行多目标求解。
3.1.1社会等级分层

3.1.2包围猎物
搜索猎物时,灰狼会逐渐接近并包围猎物,灰狼活动行为的数学模型为
D=C⊙Xp(t)-X(t)
(6)
X(t+1)=Xp(t)-A⊙D
(7)
A=2ar1-aE
(8)
C=2r2
(9)
式中,⊙表示Hadamard乘积操作;A、C为协同系数向量;Xp(t)为最优工艺参数解的位置向量;X(t)为当前工艺参数解的位置向量;X(t+1)为第t+1次迭代时工艺参数解的位置向量;D为当前候选工艺参数解与最优工艺参数解之间的距离;a为更新系数;随机向量r1和r2中的元素取值区间为[0, 1];E为元素全为1的向量,与r1的维数相同。
本文主要改进a的变化方式,为使狼群能够在更大范围内搜索目标,a的更新方式为
a=ainit-exp(-lt/T)
(10)
式中,ainit表示初始值更新系数值;l为调节系数;T为迭代次数。
3.1.3狩猎
为模拟灰狼的搜索行为,选出最佳候选工艺参数解的位置,在每次迭代寻优过程中,利用狼群中的α狼、β狼、δ狼来识别潜在猎物的位置,保留α狼、β狼、δ狼各自的位置信息,并根据已保留的位置信息搜索候选狼(包括ω狼)的位置信息。具体的狩猎行为及数学模型如图1所示,图中的R为猎物定义的随机圆半径,可以看出,候选狼的位置最终落在α狼、β狼、δ狼定义的随机圆内,即α狼、β狼、δ狼首先预测出潜在猎物(加工能耗、齿轮加工质量)的可能区域,然后候选狼在α狼、β狼、δ狼的指引下在猎物附近随机更新位置信息。

图1 灰狼狩猎行为及数学模型Fig.1 Hunting behaviors and mathematical models of grey wolf
3.1.4攻击猎物
目标猎物停止移动时,狼群攻击猎物以完成整个捕食过程。当向量A的元素大于1时,灰狼尽量分散开,扩大搜寻猎物的范围;当向量A的元素小于-1时,候选狼的下一个位置可以是现在的位置或是猎物的位置;当向量A的元素取值在[-1, 1]之间时,狼的下一个位置是当前位置和猎物位置之间的任何位置。整个优化过程根据灰狼位置的改变不断进行更新,直到得到最优的工艺参数。
基于改进MOGWO算法的工艺参数寻优流程如图2所示。
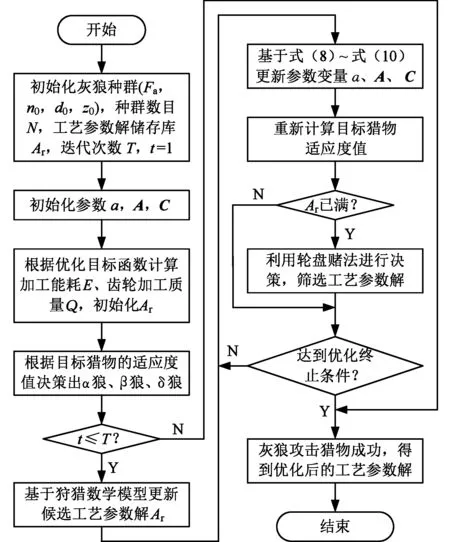
图2 基于改进MOGWO算法的工艺参数寻优流程图Fig.2 Processing parameter optimization flow chart based on improved MOGWO algorithm
3.2 基于TOPSIS的工艺参数解集性能评估
TOPSIS是一种针对现有评估指标进行优劣性能评价的方法[15],本文利用TOPSIS在决策问题上的优势,建立工艺参数性能决策矩阵,综合考虑加工能耗、齿轮加工质量与滚齿工艺参数之间的关系,对工艺参数解集的综合性能进行评估,具体的工艺参数性能排序过程如图3所示。
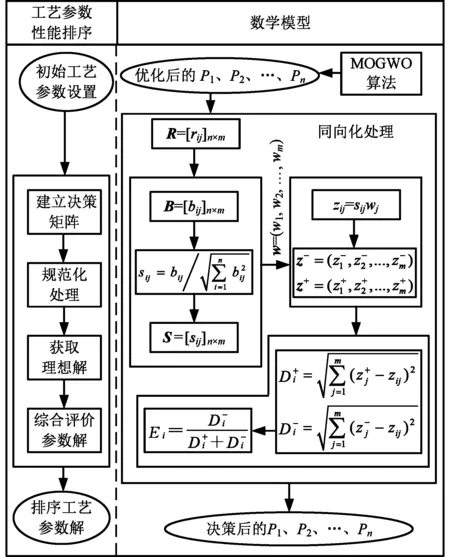
图3 工艺参数性能排序过程图Fig.3 Process chart of processing parameter performance sequencing
4 实验验证
笔者采用YE3120CNC7高速干切滚齿机加工小模数齿轮,加工中与能耗有关的参数[11]取值如下:Ps=2200 W,ts=5 min,Psc=200 W,κ1=-0.078,κ2=0.2× 10-5,ε1=0.035,ε2=0.13×10-4;齿轮加工质量权重系数w1=w2=0.5。与加工过程有关的参数取值如下:mn=2.5 mm,z2=45,αn=20°,β0=17°,B=45 mm,Ein=2 mm,Uout=2 mm,La=21.168 mm,Lr=104.5 mm,vr=1500 mm/min,ap=8.45 mm,k=17,js=1。与切削力相关的参数[12]取值如下:C=18.2,X=1.75,Y=0.65,Z=0.81,U=0.26,V=0.27,K1=1,K2=1.05,K3=1.11。
基于MATLAB编写改进MOGWO算法,设置灰狼数目N=20,最大迭代次数T=200,参数维度为4,网格数目为10,网格膨胀参数为0.1,初始更新系数ainit=2,调节系数l=2,各工艺参数的取值范围为
68 mm/min≤va≤92 mm/min 650 r/min≤n0≤780 r/mind0=78 mm,79 mm,…,89 mmz0=2,3
经过算法迭代后的工艺参数解集如表1所示,迭代寻优过程如图4所示。

表1 经MOGWO寻优后的工艺参数解集Tab.1 Solution sets of process parameters optimizedby MOGWO
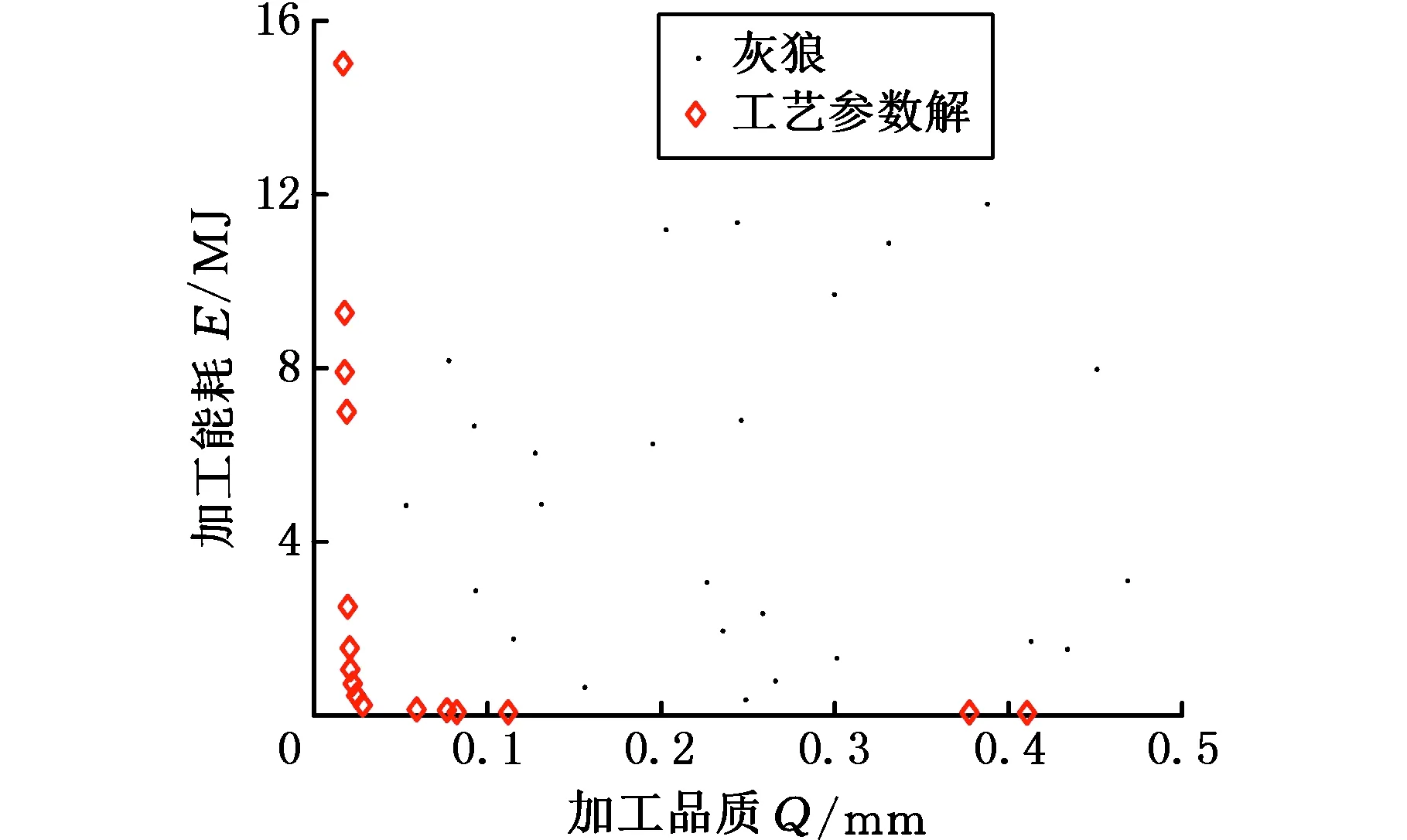
图4 迭代寻优结果Fig.4 Iterative optimization results
分析上述结果发现,随着Q的增大,E逐渐减小。上述解中的滚刀头数z0=3的解集方案较多,增加滚刀头可以缩短滚齿切削时间,降低切削阶段的加工能耗。由表1可知,寻优后得到16个工艺参数解,获取的解中存在着一些劣解,解P8、P9的性能需要基于TOPSIS进行重新评估。表1中,滚刀直径d0=89 mm对应的工艺参数解较多,更大的直径可以适当缩短齿轮切削时间以提高生产效率,此外,大直径滚刀使得滚刀内孔相对较大,增大滚刀的刚性,延长使用寿命。
由图5可以看出,va与E、Q之间没有一个确定的约束关系,较大的va会导致较小的加工能耗和较大的滚齿误差;较大的n0会导致较高的加工能耗和较大的滚齿误差。由此可知,要获取最小的加工能耗和最优的齿轮加工质量,需要考虑实际加工对加工能耗和齿轮加工质量的要求,对优化后的工艺参数解集进行决策。
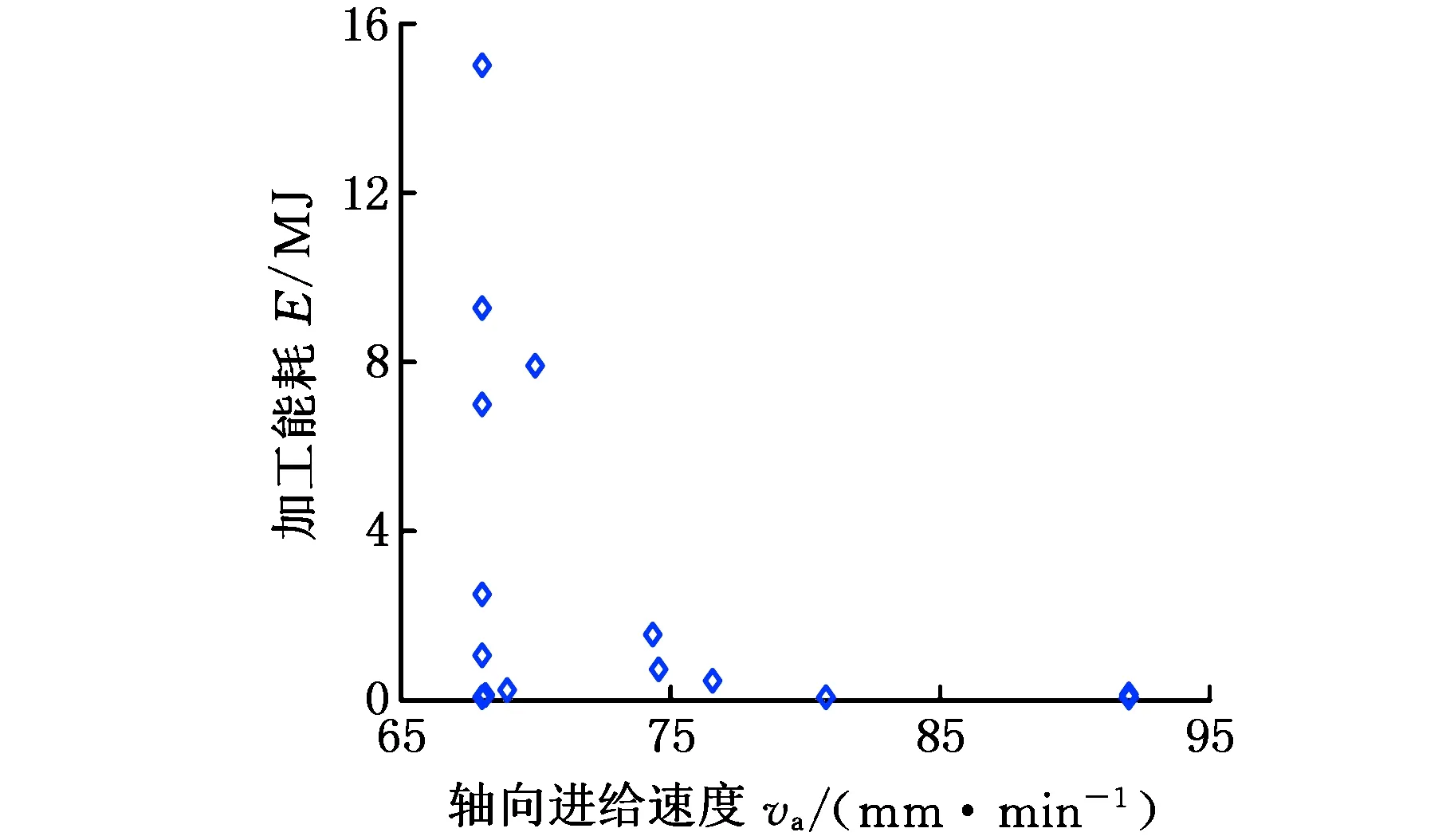
(a)va-E关系图

(b)va-Q关系图
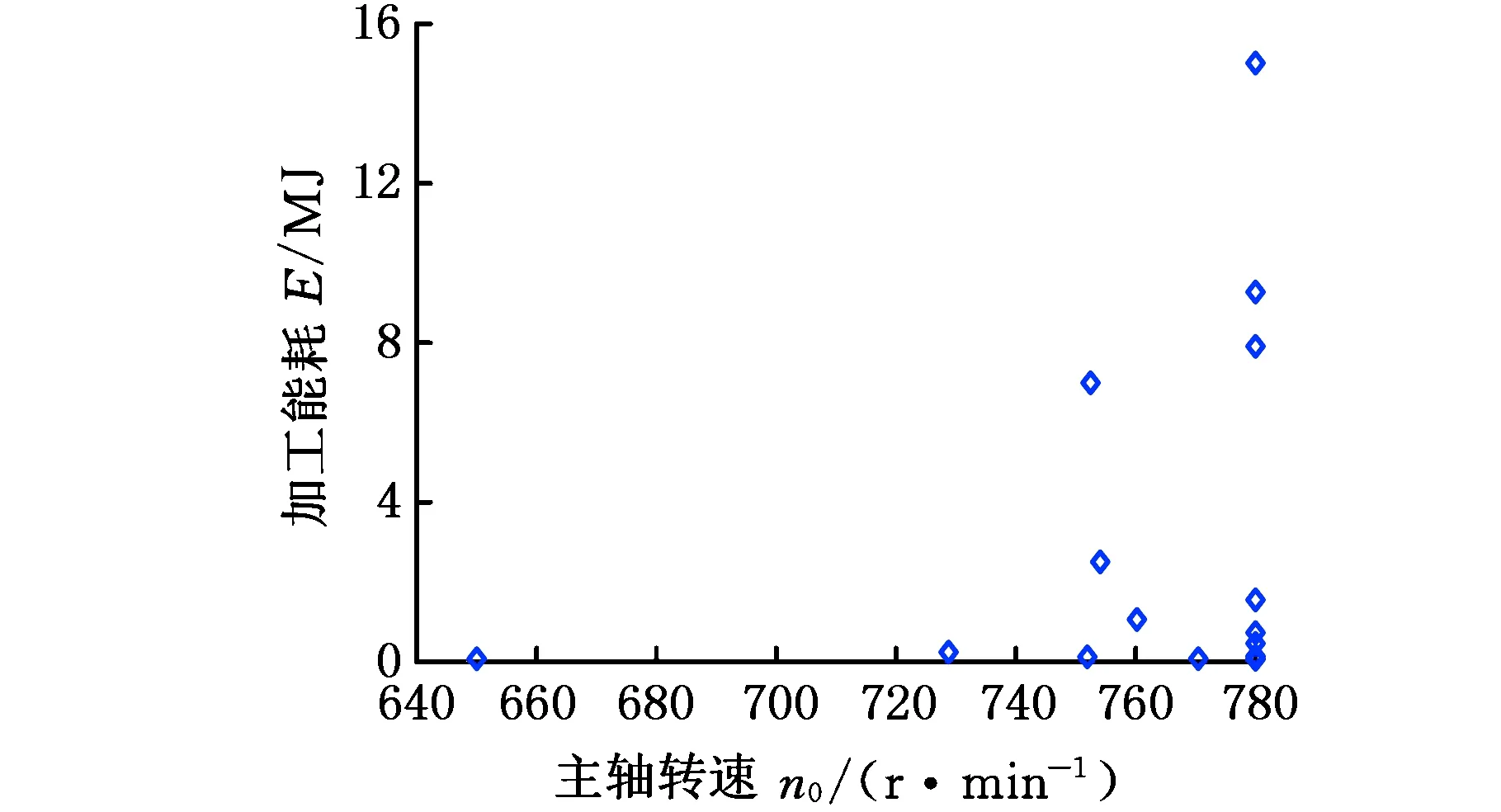
(c)n0-E关系图

(d)n0-Q关系图图5 工艺参数变量与优化目标之间的关联关系图Fig.5 Relation diagrams between process parameter variables and optimization objectives
为了获取直观明确的工艺参数解,以最小加工能耗和最优齿轮加工质量为目标,将minE、minQ作为工艺参数解性能评价指标,对MOGWO算法寻优得到的工艺参数解进行多属性决策。加工能耗、齿轮加工质量分别为环境评价指标和经济评价指标,对滚齿加工的影响作用是相同的,因此本文设置权重wE=wQ= 0.5,并按照图3所示的流程建立决策矩阵,依次进行矩阵规范化处理、理想解获取、参数解综合评价,以评估出性能更优的工艺参数解,决策后的工艺参数解如表2所示。
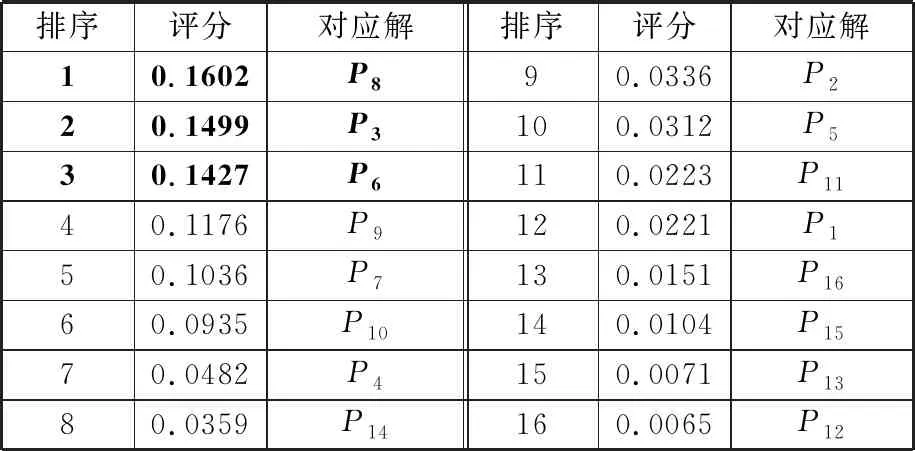
表2 决策后的工艺参数解集Tab.2 Solutions of decisive processing parameters
由表2中的评分可看出工艺参数解P8、P3、P6为相对较优的解,解P8调整后的工艺参数va=68 mm/min,n0=780 r/min,d0=89 mm,z0=3可优先作为滚齿加工的工艺参数。以提高齿轮加工质量为首要目标时,应采用解P8对应的工艺参数;以降低能耗为首要目标时,应采用解P3对应的工艺参数,即va=92 mm/min,n0=780 r/min,d0=89 mm,z0=3。根据优化结果,工艺人员可按照实际加工要求选取合理的工艺参数解集,在加工能耗和滚齿加工质量上达到一个最优的平衡。
为了进一步验证本文所提方法的有效性,采用标准灰狼算法构建多目标优化模型,算法基本参数与前文保持一致,采用TOPSIS对结果进行排序和决策。2种方法获取的最优解如表3所示,本文所提方法使加工能耗降低了5.59%,齿轮误差降低了23.53%。
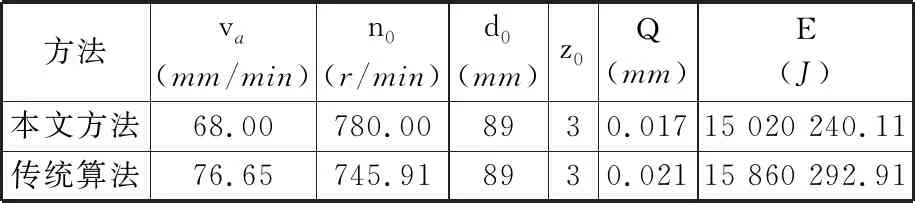
表3 结果对比Tab.3 Comparison of results
5 结论
(1)基于高速干切滚齿工艺过程,分析了滚齿工艺参数,将轴向进给速度、主轴转速、滚刀直径、滚刀头数作为待决策变量,系统分析了滚齿加工能耗的构成及齿轮加工质量的表征形式,构建了以最小加工能耗、最优加工质量为目标的多目标优化模型。
(2)本文利用改进MOGWO算法对多目标优化模型进行求解,获取了多组工艺参数解,并通过TOPSIS对优化的工艺参数解进行多属性决策,得到性能评估后的工艺参数解集。与传统灰狼算法优化结果的对比验证了本文方法的有效性。
本文针对加工能耗和齿轮加工质量进行了综合优化,为体现本文方法及结果的实用性,后续将开展相关的切削试验。另外,考虑到废弃刀具带来的环境问题,如何建立工艺参数与刀具能耗、刀具寿命之间的关联关系,将是下一步的研究方向。
